基于灰色GM（1，1）模型的河北省农村居民人均消费水平预测分析

徐林娜

近年来河北省经济得到快速发展，居民生活水平与消费水平正在逐步提高。与此通时，河北省农村居民人均消费水平与其他省份的差距不断拉大，农民的消费问题和本省的民生和经济情况息息相关。本文依据2010年-2015年河北省农村居民人均消费数据，采用灰色系统中的GM（1，1）模型对农村居民人均消费情况进行预测，为在农村开展精准扶贫工作和制定新一轮的经济政策提供科学的理论支撑。

GM （1，1）模型

农村人均消费 预测

引言

河北省作为农业大省，乡村人口数约占全省总人口的一半。要实现全面建设小康社会的目标，重点、难点在农村。近年来，中央的相关文件和诸多学者反复强调，当前农业和农村发展存在的突出问题是农民增收困难。农民的消费水平很大程度上取决于收入高低。因此，通过对河北省农村居民人均消费水平的研究，有利于我们充分认识我省农村消费及发展现状，进而采取有效措施，推进农村经济结构的战略性调整，争取早日迈进小康社会。

目前能进行预测的定量研究方法有：回归分析法、神经网络法及灰色CM （1，1）模型法等。由于灰色GM （1，1）预测模型法具有所需数据少、精度较高的特点而得到广泛的应用。本文针对河北省农村居民近年数据少，采用GM（1，1）模型对近6年河北农村居民建立预测模型并对未来3年的农村人均消费水平进行预测。

灰色预测模型建立

1982年我国著名学者邓聚龙教授提出灰色系统理论。建模时不需要大量的时间序列数据就能够取得较好的预测效果。CM（1，1）模型是灰色系统理论的基本内容之一，具体模型建模步骤如下：

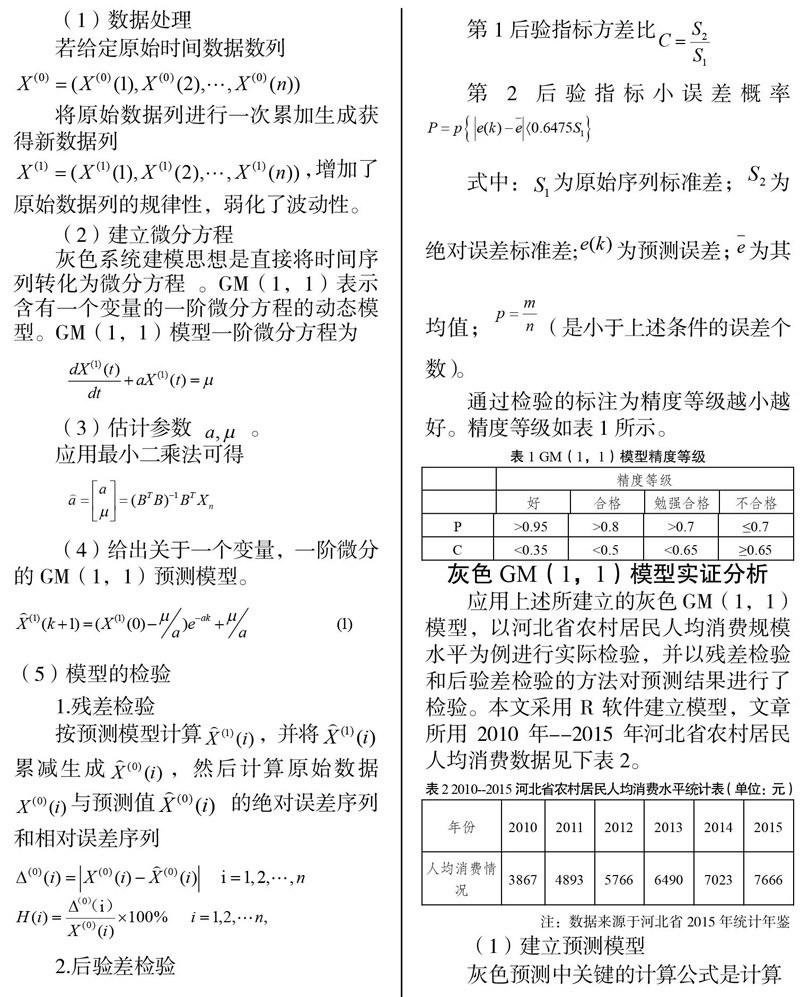
（1）数据处理

若给定原始时间数据数列X_（0）=（X_（0）（1），X_（0）（2），…，X_（0）（n））

将原始数据列进行一次累加生成获得新数据列X_（1）=（X_（1）（1），X_（1）（2），…，X_（1）（n）），增加了原始数据列的规律性，弱化了波动性。

（2）建立微分方程

灰色系统建模思想是直接将时问序列转化为微分方程。GM（1，1）表示含有一个变量的一阶微分方程的动态模型。GM（1，1）模型一阶微分方程为

dXsub>（1）

1.残差检验由表2的实际值与表3的预测值计算出原始序列Xsub>（0）