粮食价格波动分析

杨璇 张浩 崔梦宵

改革开放以来，我国粮食价格波动经历了一个曲折过程，具有明显的阶段性。粮食价格波动的经济效应主要是影响粮食生产、农民收入和市场价格总水平。本文利用ARCH、GARCH、TARCH和EGARCH等ARCH类模型对粮食价格的波动、波动的非对称性进行了分析。并得出结论：可以利用价格波动的集簇性对未来的价格波动进行分析；要不断完善粮食市场，引导市场参与主体理性投资；要特别关注价格波动规律并采取相应措施。

粮食价格

波动分析 ARCH类模型

引言

民以食为天，粮食是人类生存的主食品，是基本的物质基础，更是一个国家的战略物质。没有粮食，就不要谈国家的稳定。基本温饱无法解决，其他的发展就只是空想，是空中楼阁。列宁说：真正的经济基础是粮食储备，没有它社会主义制度只是一个愿望。而不稳定价格会导致粮源不足，在总量上不能满足市场的需要。而且不能有个买卖双方都接受的合理价格。因此，稳定的粮食价格在实现粮食安全的过程中有举足轻重的作用。

本文运用稻谷、小麦、玉米的月度价格数据，采用ARCH类模型，对粮食价格波动性进行分析，从而更好地掌握粮食市场价格规律，以更好地确保粮食价格基本稳定，避免其大幅度波动，从而保障国家粮食安全。

文献综述

粮食价格波动问题一直备受关注，有很多学者从不同角度进行了研究。关于粮食价格波动的特点，冯云（2008）的研究表明，粮食价格波动具有集簇性和明显的非对称性。关于粮食价格波动的影响因素，Lapp and Smith（1992）认为，粮食价格波动水平直接和间接受到宏观经济政策特别是货币政策的影响；钟甫宁（1995）强调了稳定的政策和统一的市场对避免粮食价格人为波动的重要性；柯炳生（1996）认为，农户的粮食储备及其市场反应行为是造成粮食价格波动的重要原因之一；谭江林、罗光强（2009）的研究表明，通货膨胀是粮食价格波动的Granger原因。关于粮食价格波动产生的影响，石敏俊、王妍、朱杏珍（2009）的研究表明，能源价格和粮食价格上涨及其带来的饲料价格上涨和劳动力成本上升所导致的成本驱动效应对畜产品价格实际涨幅的影响在44%-59%之间；对加工食品价格的影响较为显著，占加工食品价格实际涨幅的74%左右。能源价格上涨对CPI和物价总水平的拉动作用高于粮食价格波动的影响。受粮食价格上涨的影响，城镇居民净收益减少，农村居民净收益增加。何蒲明、黎东升（2009）认为，中国粮食产量与价格波动均较大，并且价格波动比产量波动更大，对国家粮食安伞造成了不利影响；而粮食产量与粮食价格有密切的关系，粮食价格是粮食产量变化的原因。

从研究方法上来说，国外研究价格波动问题常常采用ARCH类模型。ARCH类模型能准确地模拟时间序列变量的波动，使人们能更加准确地把握波动（风险）。国内应用ARCH类模型的研究成果也比较丰富，现有的研究成果主要集中在股票市场和期货市场方面。比如，陈千里（2002）利用GARCH类模型，以上证综合指数为对象，对中国股市波动进行了实证研究，并在中国股市的背景下对集簇性和不对称性的几种经济解释进行了理论分析。华仁海、仲伟俊（2003）运用ARCH类模型对中国期货市场中期货价格、收益、交易量、波动性相互之间的关系进行了动态分析。刘宁（2004）应用ARCH类模型对上海股市的波动进行了分析。唐衍伟、陈刚、张晨宏（2004）运用ARCH类模型对中国铜、大豆、小麦期货市场的波动和有效性进行了研究。

总的来说，关于粮食价格波动和ARCH类模型应用的研究成果非常丰富，为本文的研究提供了参考和借鉴。但是，现有研究还有进一步拓展的空间：一是目前关于粮食价格波动的描述性分析较多，但计量分析较少；二是利用ARCH类模型研究粮食价格波动的成果很少，冯云（2008）的研究没有分具体粮食品种，从实际情况看，不同粮食品种价格的波动存在差异，因而有必要细分品种来研究。

研究方法与数据说明

本文使用了2005年1月至2014年12月的集贸市场月度价格（元，公斤）数据，数据来源于国家统计局农村社会经济调查司：《中国农产品价格调查年鉴》（2005-2014年，历年），中国统计出版社。

主要研究方法如下：

（1）波动分析

1.ARCH模型

高频金融时问序列数据建模后的残差具有异方差特性和自相關性，这种特征被称为“ARCH效应”。而ARCH自回归条件异方差）模可以较好的刻画金融时问序列的“ARCH效应”，该模型假定随机误差项的条件方差与其误差项滞后的平方有关。ARCH模型的核心思想是，误差项在时刻T的方差依赖于时刻T-1的残差平方的大小。因此，在ARCH模型中，要涉及两个核心的模型回归过程，即原始的回归模型（常常被称为条件均值回归模型或均值方程）和方差的回归模型（常被称为异方差回归模型或者方差方程）。ARCH模型由以下两个方程组成：R_t= X'γ₀+ε_t（1）h_t=α₀+∑_αi=1α_iε_2t-i（2）

（1）式称为均值方程，其中，R_t为被解释变量，在本文中表示粮食价格收益率，X为解释变量，在本文中只包括R_t的滞后项；（2）式称为方差方程，其中，表示ε_t在t时刻的条件方差，在方差方程中它被定义为残差滞后项的加权平方以确保条件方差h_tt>0。∑_αi=1α_iε_2t-i为ARCH项，如果ARCH项0高度显著，说明粮食价格收益率有显著的波动集簇性。

2.GARCH模型

又称广义自回归条件异方差模型，即在ARCH模型的基础上，加入条件方差自身的滞后项就可得到：h_t=α₀+∑_qi=1α_iε_2t-i+∑_pj=1β_jh_t-j（3）

（3）式中，∑_qi=1α_iε_2t-1为ARCH项，∑_pj=1β_ih_t-1为GARCH项，p和q分别为它们的滞后阶数，如果ARCH项和CARCH项都高度显著，说明粮食价格收益率具有显著的波动集簇性。为保证条件方差h_t非负，一般要求系数α≥0和β_j≥0，但这个系数的非负性要求只是保证模型有意义的充分条件而非必要条件。CARCH模型将波动来源划分为两部分：变量过去的波动h_t-i和外部冲击ε_2t-i，而α_i和_jβ则分别反映了它们对本期波动h_t的作用强度。模型系数之和∑_qi=1α_i+∑_pj=1β_j的大小反映了波动的持续性，当它小于1时，说明冲击的影响会逐渐消失，当它大于1时，说明冲出的影响不但不会消失，反而会扩散。相对于ARCH，GARCH模型的优点在于：可以用较为简单的GARCH模型来代表一个高阶ARCH模型，从而使模型的识别和估计都变得比较容易。

（2）波动非对称性分析

1 .TGARCH模型

TARCH模型由Rahemananjara andZokoian（1993）提出，条件方差方程为：h_t=α₀+α₁ε_2t-1+β₁h_t-1+φd_t-1ε_2t-1（4）

（4）式中，d_t-1是虚拟变量，当ε_t-1<0时，d_t-1，否则d_t-1=0。此模型中，价格上涨信息（ε_t≥0）对条件方差的影响为α₁，而价格下跌信息（ε_t<0）的影响为α₁+φ。如果φ≠0，表明波动具有非对称性。当φ>0时，表明价格下跌信息引发的波动比价格上涨信息引发的波动大；当φ<0时，表明价格上涨信息引发的波动比价格下跌信息引发的波动大。

2.ECARCH模型

ECARCH模型由Nelson（1991）提出，其条件方差方程为：

（5）式中，价格上涨信息（ε_t-1≥0）對Lnh_t的影响为α+γ，价格下跌信息（ε_t-1<0）的影响为α-γ。如果γ≠0，表明波动具有非对称性。当γ>O时，表明价格上涨信息引发的波动比价格下跌信息引发的波动大；当γ<0时，表明价格下跌信息引发的波动比价格上涨信息引发的波动大。

数据统计分析

价格收益率以相邻月份粮食价格的对数一阶差分表示，R_t= Lnp_t-Lnp_（t-1）2其中，p_t和p_（t-1）分别表示第t月和第t-1月的价格。

关于价格收益率的有关统计量分析如下：

结果表明：小麦、籼稻、粳稻价格收益率的峰度都高于正态分布的峰度值3，说明价格收益率具有尖峰和厚尾特征；JB正态性检验也证实了价格收益率显著异于正态分布。小麦、籼稻、粳稻、价格存在波动的集聚现象和异方差效应。

模型结果估计

单位根检验平稳性检验结果表明：小麦价格序列平稳，籼稻和粳稻价格序列非平稳，而收益率序列都平稳。

（1）小麦

对小麦价格进行ARCH类模型估计，步骤如下：

1.根据分析结果建立均值模型Y_t=0.002700+0.356315Y_t-1

通过小麦残差序列图可得小麦残差序列很可能存在ARCH效应。

2.CARCH模型估计结果：

根据p值判断，ARCH和CARCH项都高度显著，说明具有波动集簇性。

因此进行非对称GARCH模型的估计。

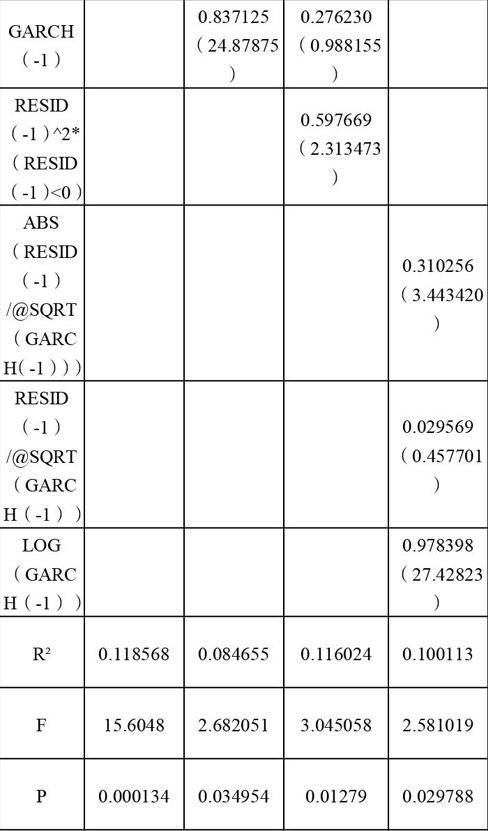
3.根据TGARCH、EGARCH模型估计结果可知，各项系数在10%的显著性水平下均显著。这说明小麦价格波动具有显著的非对称性。

（2）籼稻

对籼稻价格进行ARCH类模型估计，步骤如下：

1.根据分析结果建立均值模型

Y_t=0.003258+0.344058Y_t-1

通过籼稻残差序列图可得籼稻残差序列很可能存在ARCH效应。

2.CARCH模型估计结果：

根据p值判断，ARCH和GARCH项都高度显著，说明具有波动集簇性。

因此进行非对称CARCH模型的估计。

3.根据TGARCH、EGARCH模型估计结果可知，各项系数在10%的显著性水平下均显著。这说明籼稻价格波动具有显著的非对称性。

（3）粳稻

对粳稻价格进行ARCH类模型估计，步骤如下：

1.根据分析结果建立均值模型

根据分析结果建立均值模型

r_t=0.003518+0.298560Y_t-1

通过粳稻残差序列图可得粳稻残差序列很可能存在ARCH效应。

2.CARCH模型估计结果：

根据p值判断，ARCH和CARCH项都高度显著，说明具有波动集簇性。

因此进行非对称CARCH模型的估计。

3.根据TGARCH、EGARCH模型估计结果可知，各项系数在10%的显著性水平下均显著。这说明粳稻价格波动具有显著的非对称性。

通过对小麦、籼稻、粳稻价格波动进行分析，得出以下结论：小麦和玉米价格波动具有显著的集簇性。小麦价格波动具有非对称性，即价格上涨信息引发的波动比价格下跌信息引发的波动大。

与现实相联系，模型估计结果表明：一是，小麦、籼稻、粳稻市场大的价格波动后面往往跟随着大的价格波动，小的价格波动后面经常跟随着小的价格波动，这说明，小麦、玉米价格波动在一定程度上是可以预测的。小的价格波动影响较小，但大的价格波动会对粮食产业发展、居民生活、宏观经济产生较大的影响，为稳定粮食市场，大的价格波动不可不防。二是，粮食市场没有体现出高风险高回报、低风险低回报的特征，这说明，中国粮食市场的大部分交易者在做决策时非理性因素大于理性因素，中国粮食市场有待进一步发展和完善。三是，对粮食市场来说，价格上涨信息引发的波动比价格下跌信息引发的波动大。为稳定粮食市场，要特别关注引起粮食价格上涨的因素并采取相应措施。

总结和讨论

国内粮食价格的变化关系直接到农民和消费者的切身利益。为维护人民群众的切身利益和国家粮食安全，中国政府对国内粮食市场实行严格宏观调控：建立了储备粮制度、粮食价格托市制度等，同时对粮食进口实行严格的配额管理。通过这些制度，中国国内粮食市场价格受国际粮食市场影响较小。国内粮食价格能够充分反映中国国内粮食的供给和需求情况。粮食价格指数是衡量粮食价格变动程度的重要指标。“十三五”期间（2016-2020年）是中国全面建成小康社会的重要时期，分析和预测“十三五”期间各年国内粮食价格指数，使国家根据粮食价格的变化，采取必要的措施对粮食市场进行宏观调控，制定合理的国家粮食政策，做到未雨绸缪，是保持国民经济持续健康稳定发展，维护人民群众的切身利益的重要手段。

[1]冯云.《中国粮食价格波动的实证分析》，《价格月刊》2008年第2期。

[2]钟甫宁.《稳定的政策和统一的市场对我国粮食政策的影响》，《中国农村经济》1995年第7期。

[3]柯炳生，《中国农户粮食储备及其对市场的影响》，《中国农村观察》1996年第6期。

[4]谭江林，罗光强.《粮食价格波动与通货膨胀关系的实证研究》，《价格月刊》2009年第3期。

[5]石敏俊，王妍，朱杏珍.《能源价格波动与粮食价格波动对城乡经济关系的影响——基于城乡投入产出模型》，《中国农村经济》2009年第5期。

[6]何蒲明，黎东升.《基于粮食安全的粮食产量和价格波动实证研究》，《农业技术经济》2009年第2期。

[7]陈千里.《中国股市波动集簇性和不对称性研究》，《湖北大学学报（自然科学版）》2002年（第24卷）第3期。

[8]华仁海，仲伟俊.《我国期货市场期货价格收益、交易量、波动性关系的动态分析》，《统计研究》2003年第7期。

[9]唐衍伟，陈刚，张晨宏.《我國期货市场的波动性与有效性——基于三大交易市场的实证分析》，《财贸研究》2004年第5期。

[10]刘宁.《对上海股票市场波动性的ARCH研究》，《兰州大学学报（自然科学版）》2004年（第40卷）第6期。