混合地理加权回归模型的理论及其应用

赵 静,蒲 越

(新疆财经大学 应用数学学院，乌鲁木齐 830012)

在空间数据分析中，虽然普通的线性回归模型作为一种最普通最常用的方法，可以用来分析自变量与应变量之间的关系，但普通的线性回归模型未能描述空间位置的特殊性——空间非平稳性或空间异质性，因而不能全面有效地反映出空间数据的真实属性。[1]近年来，多名学者对混合地理加权回归模型进行了研究，混合地理加权回归模型作为一种有效的探测空间数据分析法已经广泛应用在各个领域。例如，Pecci等研究15个欧盟国家的农业生产力，通过MCMC检验，以人口密度、GDP为全局变量，以失业率和林业面积为局部变量，通过MGWR基础建立模型，得出区域农业生产力的空间分异；[2]Helbich通过考察建筑和住宅对周围环境的影响建立MGWR模型，对奥地利的房价进行研究，认为局部变量对房价的影响较大，房价会随空间局部变量的变化而变化[3]；覃文忠等通过迭代算法，深入分析了混合地理加权回归模型的参数，将模型的参数进行了分类，并以上海市住宅小区楼盘销售平均价格为例进行验证，最终得出混合地理加权回归模型大于地理加权回归模型，且拟合度更好，局部参数更稳健。[4]本文主要通过两步估计法对混合地理加权回归模型的参数进行有效的分类，得到混合地理加权回归模型的常参数和变参数的表达式，选取国内31个省(市、自治区)的SO2排放量为例进行研究分析。

一、混合地理加权回归模型(MGWR)理论方法及估计

(一)混合地理加权回归模型的理论

混合地理加权回归模型是对地理加权回归模型的进一步扩展。在混合地理加权回归模型中，将部分因子在整体范围中保持不变的量称为全局变量，而另一部分因子会随着空间地理的变化发生改变，称为局部变量。模型表达式为

(1)

式中：i=1,2,…,n；βj(j=0,1,…,q)为未知常数，而βj(ui,vi)(j=q+1,q+2,…,p)为第i个观测点(ui,vi)处的未知参数(ui,vi)的任意函数。

也可以写成矩阵形式

(2)

其中：i=1,2,…,n；

满足

地理加权回归模型是对回归模型中局部参数进行研究，而混合地理加权回归模型是针对回归模型中参数进行全局研究。因此，实际应用中对于参数的估计问题，地理加权回归模型参数估计并不适用于混合地理加权回归模型中的参数估计。对于混合地理加权回归模型的参数估计问题，通常选取两步估计法和Back-Fitting估计法。[5]本文采用后一种估计方法。

(二)混合地理加权回归模型的两步估计法

混合地理加权回归模型(MGWR)由两部分构成：常系数部分和变系数部分。若用地理加权回归模型估计这两个部分，将会产生两个新的因变量的估计值Yc和Yg，[6]表达式为

Yc=Yc(Y-Yg)，

(3)

式中Yc和Yg分别为

假定βc=(β0,β1,…,βq)T是对常参数的估计值，将Yc=Xcβc代入，得出

从而得到

最终解出

(4)

可知因变量的估计值为

(5)

其中

(6)

由于式(6)为已知，通过地理加权回归模型可计算变参数的部分，常参数部分通过用最小二乘法估计，分别获取参数的估计值及因变量的拟合值。可将混合地理加权回归模型写为

(7)

式中：i=1,2,…,n。

矩阵形式表示

(8)

变参数在地理位置(ui,vi)的估计值为

(9)

将式(7)转化为

得出

(10)

可得出常系数的估计值为

(11)

因而得出

(12)

其中

二、实证分析

(一)数据选取

选取国内31个省(市、自治区)，对经济指标和空气环境指标进行分析，其中样本选取的变量有：人均第一产业额SO2排放量、就业率、人口密度以及人均电力消费。具体设计如表1所示，数据来源于《中国统计年鉴》和《中国环境统计年鉴》。

表1 模型指标设计

(二)空间自相关分析

首先，在建立模型之前进行自相关检验。空间自相关分析出空间异质性和依赖性，通过Moran′sI指数反映出空间邻近区域之间的相似程度，取值介于-1和1之间，大于零表示正相关，小于零表示负相关，等于零表示不存在空间相关性或各个要素之间差异性较小。计算式为

(13)

对于Moran′sI指数的计算结果，有渐进分布和随机分布两种检验方法。对Moran′sI进行标准化通常采用标准化的Z统计量

(14)

通常统计量Z值服从标准正态分布，同时显著性也由正态分布判断。根据空间单元的数量和分布的特征可以计算标准化Moran′sI期望值

(15)

对2015年国内31个省(市、自治区)SO2排放量在空间上的自相关、空间依赖性及集聚性方面进行检验，基于对距离的空间权重矩阵，利用全局Moran′sI指数计算SO2排放量的集聚情况，结果见表2。

表2 全局Moran′sI指数

国内31个省(市、自治区)SO2排放量的Moran′sI指数为0.338，Z值大于正态分布函，即在1%水平下的临界值(1.96)，表明各省之间SO2的排放量在地理位置上具有一定的正自相关(即空间依赖性)，说明SO2在空间的分布并不是随机的，而是呈现出一种较强的集聚现象。此外，均值和方差数值较小，表明结论可靠。

表3 Moran′sI值及P值

由表3可知，变量人口密度和人均第一产业额的P值均小于0.05，说明具有明显的空间异质性和空间集聚性，因而可作为局部变量；人均电力消费和就业率的P值均大于0.05，但并不显著，空间异质和集聚性表现不够明显。

(三)混合地理加权回归模型两步估计法应用分析

通过上述检验，可将混合地理加权回归模型参数进行分类，见表4。

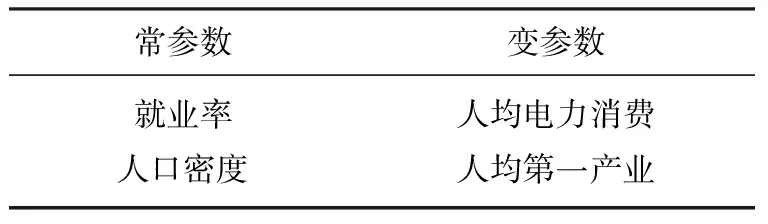
表4 混合地理加权回归模型参数分类

建立混合地理加权回归模型，用两步法估计出模型各个参数的P值及拟合值，计算式为

lnyi=β0+β1lnx1i+β2lnx2i+
α(u1i,v1i)lnZ1i+α(u2i,v2i)lnZ2i

(16)

表5 两步法参数估计的检验P值

由表5可以看出，两步法估计得到的参数P值均小于0.05，拟合优度R2为94.2%，说明两步法对混合地理加权回归模型的估计更加精确，且拟合度很好。

通过GWR软件进一步有效描述出变量对SO2排放量的影响，对比图见图1。从图1中可以看出，(b)与(a)基本吻合，只是有部分地区不一样。新疆、黑龙江等地残差较低，说明测量值与真实值较为接近；对于少部分地区，如天津、青海等地，原始的SO2排放量属于轻度污染，而在回归拟合图中属于中度污染，这与事实基本符合。说明两步估计法能够更好地验证变量对SO2排放量的影响。[7-9]

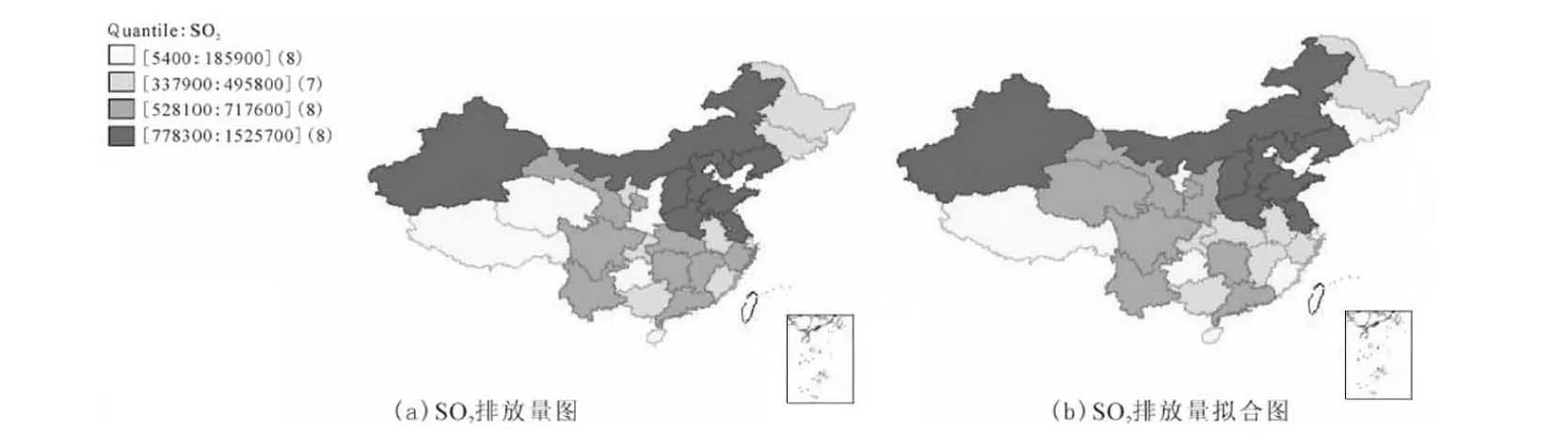
图1 SO2排放量对比图

三、结论与建议

混合地理加权回归模型中既有局部参数(变参数)，也有全局参数(常参数)，本文主要用两步估计法分别对这两部分进行计算。为了能够较好地应用混合地理加权回归模型参数估计问题，本文以国内31个省(市、自治区)为研究对象，通过对选取的变量进行空间自相关的检验和验证，将选取的变量进行分类，有效地验证了两步法对模型的显著性和拟合值。根据所选择的变量，可以看出空气污染主要是由于电力消费和第一产业所引起的。为保护环境，在绿色种植的过程中，要增加防火意识，防止发生火灾，减少因火灾带来大量的废气污染，同时，在使用电能过程中也需要提高防火意识。另外，要鼓励发展高新技术产业，通过不断发展高新技术产业，从而有效降低大气污染，改善环境。

参考文献：

[1]魏传华，梅长林.半参数空间变系数回归模型的两步估计方法及数值模型[J].统计与信息论坛，2005(1):16-19.

[2]PESSI F，SASSI M.A mix geographically weighted approach to decoupling and rural development in the EU-15[C].107th Seminar European Association of Agricultural Economists in its series，21308，Sevilla，Spain with number，6625.

[3]HELBICH M.Mixed geographically weighted regression for hedonic house price modelling in austria[D].Heidelberg：University of Heidelberg，2010.

[4]覃文忠，王建梅，刘妙龙.混合地理加权回归模型算法研究[J].武汉大学学报(信息科学版)，2007(2):115-119.

[5]玄海燕，刘树群，罗双华.混合地理加权回归模型的两种估计[J].兰州理工大学学报，2007(3)：142-144.

[6]魏传华，吴喜之.空间变系数模型的统计诊断[J].数理统计与管理，2007(6)：1027-1033.

[7]康国栋.中国经济发展的电力需求及对环境的影响分析[D].西安：陕西师范大学，2009.

[8]齐飞.混合地理加权回归模型的统计推断[D].北京：中央民族大学，2010.

[9]韦米佳.中国宏观经济内生增长因素分析：基于混合地理加权回归(GWR)模型的实证分析[J].中国经济问题，2009(3)：24-30.