基于非线性规划的太阳影子定位技术研究

黄亚群，李星宇，任莹莹，田 润，张怀雄，苏 茜

(1.云南大学 信息学院，云南 昆明 650091；2.中国科学院大学 计算技术研究所，北京 石景山 100190；3.中南大学 信息科学与工程学院，湖南 长沙 410083)

太阳影子定位技术是通过分析视频中物体的太阳影子变化，确定视频拍摄的地点和日期的一种方法[1]。为保证根据物体的太阳影子变化精确地确定拍摄地点和拍摄日期，关键在于分析影子长度关于各个参数的变化规律，建立太阳影子定位的数学模型。将直杆在阳光下产生的影子轨迹近似代替太阳运动的轨迹，根据相对运动的原理，将地球绕太阳自转和公转的运动简化为地球不动太阳绕地球转动，并将太阳绕地球的运动看作在近圆形的轨道上运行。首先，建立影子长度随日期、当地标准时间、目标所在经度和纬度及直杆长度变化的动态数学模型，从而计算并绘制太阳影子长度的变化曲线；其次，考虑影子长度随当地标准时间(北京时间)的变化曲线，以直杆所在经度和纬度及直杆长度为决策变量，以实际影子长和计算影子长之差的平方和最小为目标函数，建立太阳影子定位的非线性规划模型，结合曲线拟合选取初值，对视频信息进行预处理后提取相关数据，从而得到视频拍摄地点和日期。

1 影子长度变化模型

以直杆在阳光下产生的影子轨迹近似代替太阳运动的轨迹，并根据相对运动的原理，将地球绕太阳自转和公转的运动简化为地球不动，太阳绕地球转动，于是太阳绕地球在近圆形的轨道上运行。以直杆所处地面为参考平面，其底端为原点，以南为x轴，以东为y轴建立直角坐标，如图1所示。

设当地纬度为wd，太阳赤纬角[2]为δ，时角为Ω，太阳高度角[3]为h，太阳方位角[4]为A，则计算公式[5－6]分别为:

图1 直杆投影坐标系

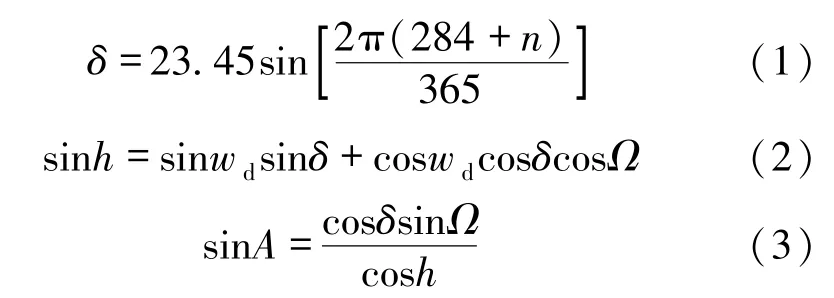
式中，n为日期序列，即某日期在一年内的顺序号，如n＝1时表示1月1日。

设直杆的高度为H，影子长度为L，则影子长度动态变化模型为:

若直杆影子顶点的坐标为P(x0，y0)，则影子顶点的横纵坐标分别为:

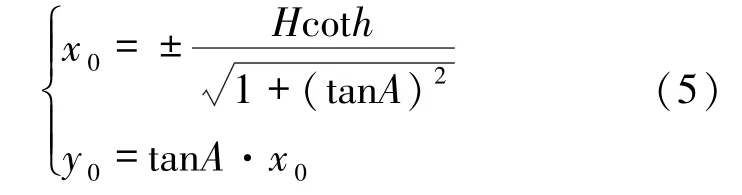
于是影子长度L关于各参数的变化规律为:

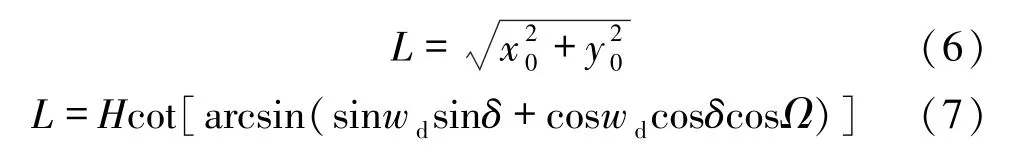
把文献[1]的附件1中数据带入式(7)，利用MATLAB编程画出直杆影子随时间的变化曲线如图2所示，影子轨迹曲线如图3所示。

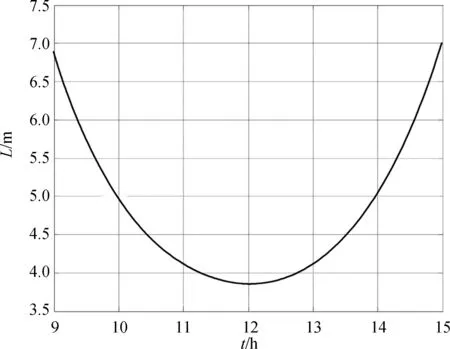
图2 影子长度时间变化曲线

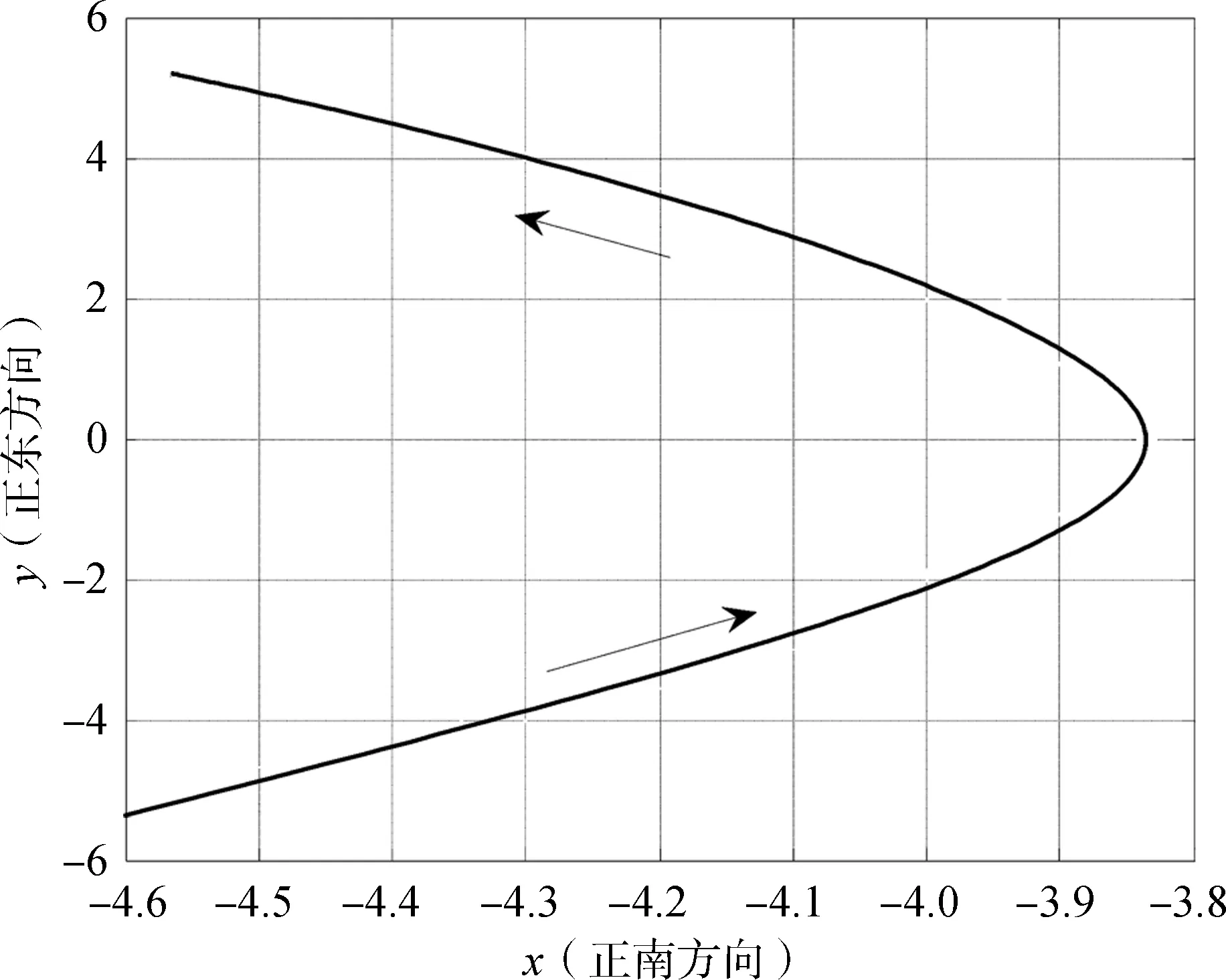
图3 影子轨迹变化曲线

2 太阳影子定位模型

确定了直杆影子长度变化规律后，根据直杆在水平地面上的影子顶点坐标数据，分别从已知和缺失拍摄的日期信息两种情况，建立非线性规划模型确定直杆所处的地点和日期，并给出若干个可能的拍摄地点和日期。

2.1 拍摄地点的优化模型

式(7)表明，影子长度L的计算值Lc由直杆所在位置的经度jd、纬度wd及直杆高度H共同决定，而第i(i＝1，2，…，21)个时刻影子顶点为(xi，yi)时的影子长度的计算值为1，2，…，21)。

在已知测量的准确日期、当地标准时间及相应时刻的影子顶点坐标等数据的情况下，建立拍摄地点的优化模型，利用影子轨迹确定直杆可能的拍摄位置的经纬度。

以直杆所在的经度、纬度及直杆的长度作为决策变量，以第i(i＝1，2，…，21)个时刻的测量影长Li和计算影长Lci间的误差最小为目标函数，将描述太阳位置的参数作为约束条件，建立太阳影子定位的非线性规划模型[7－8]:

式中，δ是太阳赤纬角，e为时差，Tt为真太阳时[9]，T为当地时间，n为日期序号，h为太阳高度角，Ω为时角，wd为当地的纬度，H为直杆长度，L为直杆的影子长度。

利用制约函数法，将求解非线性规划的问题转化为一系列无约极值问题来求解，再使用内点法，即对企图从内部穿越可行域边界的点在目标函数中加入相应的 “障碍约束”，从而保证迭代一直在可行域内部进行[5]。

利用文献[1]的附件1中数据，通过Lingo程序迭代求解[10]，得到直杆的地理位置为 (108.644 8°E，19.273 5°N)。

将测量影长Li和计算影长Lci进行对比，如图4所示。由图4可以看出，文献[1]的附件1中给定时刻的测量影长Li和该时刻对应的计算影长Lci几乎完全一致，因此使用非线性规划模型(8)能够较为精确地计算出直杆的拍摄地点。

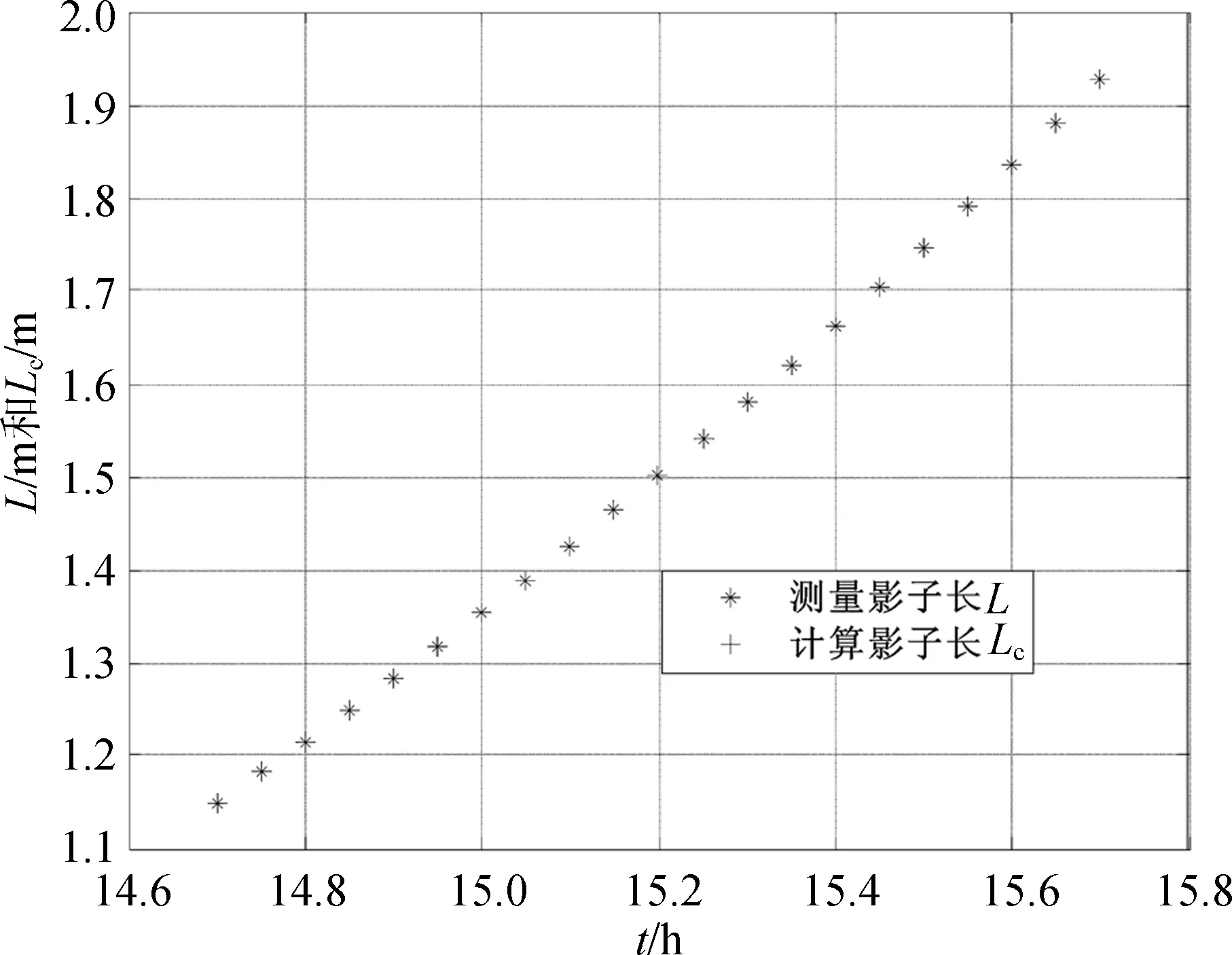
图4 测量影长和计算影长对比

2.2 拍摄时间和地点的优化模型

当缺失拍摄时间信息时，赤纬角等描述太阳位置的参数无法确定，因此采用穷举法添加日期信息，然后再建立优化模型求出全局最优解。由于非线性规划的初始值选取非常重要，所以首先采用曲线拟合的方法粗略地计算出每个日期的初始迭代值，然后对每个日期利用模型(8)进行非线性规划，并记录下每个日期的目标函数值，用该日期计算的位置信息利用式(5)求出相应时刻的影子顶点坐标，最后通过最小二乘法分析出误差最小的日期，其相应的地点即为直杆可能所在地点。

1)非线性规划初值选取——拟合粗略计算经纬度。

利用文献[1]的附件2和附件3中的时间－影子长度数据，用二次函数进行拟合，得到影子最短时的长度Lemin和此时所对应的当地标准时间TS12。

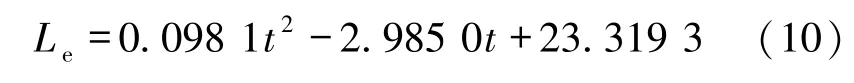
附件2中数据得到的拟合函数为:显然当t＝－b/2a时，函数有最小值，即附件2中TS12＝15.207 5 h，Lemin＝0.622 2 m。附件3中数据得到的拟合函数为:于是TS12＝12.735 4 h，Lemin＝3.483 3 m，拟合结果如图5和图6所示。

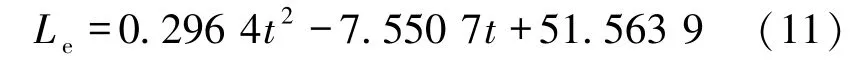
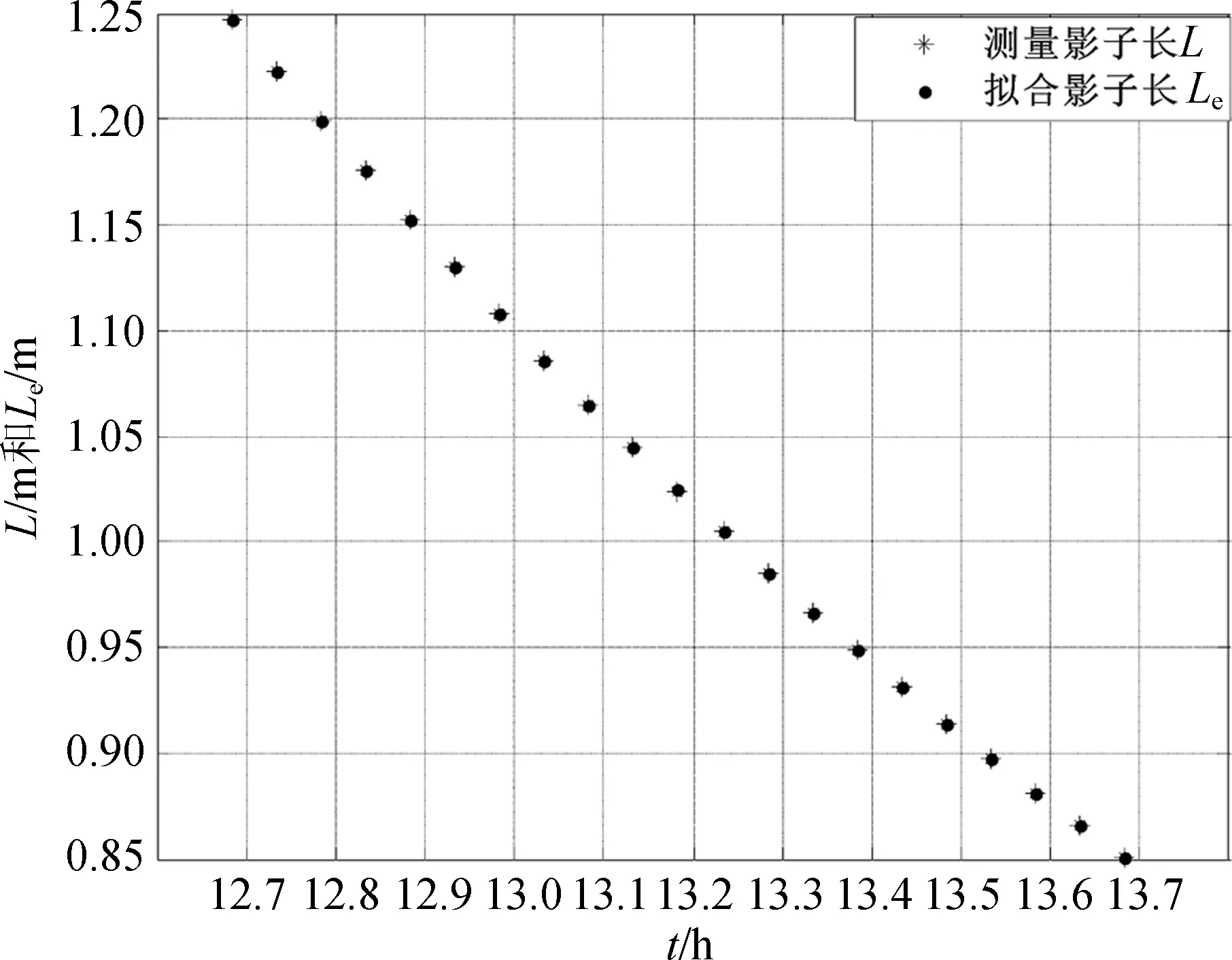
图5 附件2测量影长与拟合影长对比图

根据真太阳时和太阳高度角公式，由当地标准时间TS12、当地时间T(T＝12∶00)及直杆高度H、赤纬角δ、经度jd和纬度wd计算公式分别为:

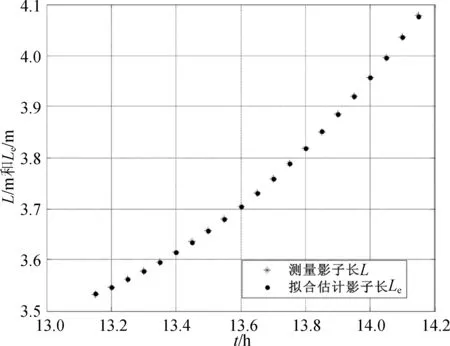
图6 附件3测量影长与拟合影长对比图

综上所述，根据式(12)和式(13)选取非线性规划中经纬度的初始值，能够得到比较优化的解。

2)基于穷举法求解非线性规划模型。

缺少日期信息的情况下，使用穷举法以每天为步长对一年中所有日期用非线性规划模型式(4)进行求解，记录下全局最优解，即该日期的经纬度的值及所有的误差，也就是目标函数的值。依据误差的大小将误差和日期按升序排列，便得到直杆位置的经纬度。

3)利用最小二乘法误差分析确定可能的日期。

将文献[1]的附件2及附件3中的数据利用非线性规划模型式(8)进行求解，进行穷举误差排序。在已升序排列的误差中，选取误差在同一量级的日期作为候选日期序号，并取出误差最小的前6个，如表1和表2所示。

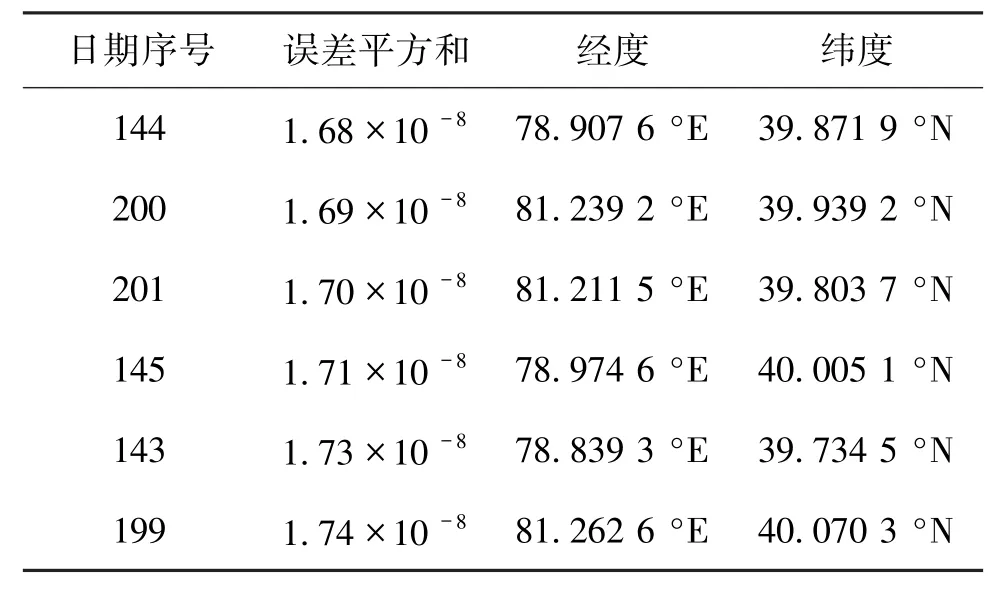
表1 附件2计算出的前6个候选日期序号及相应经纬度

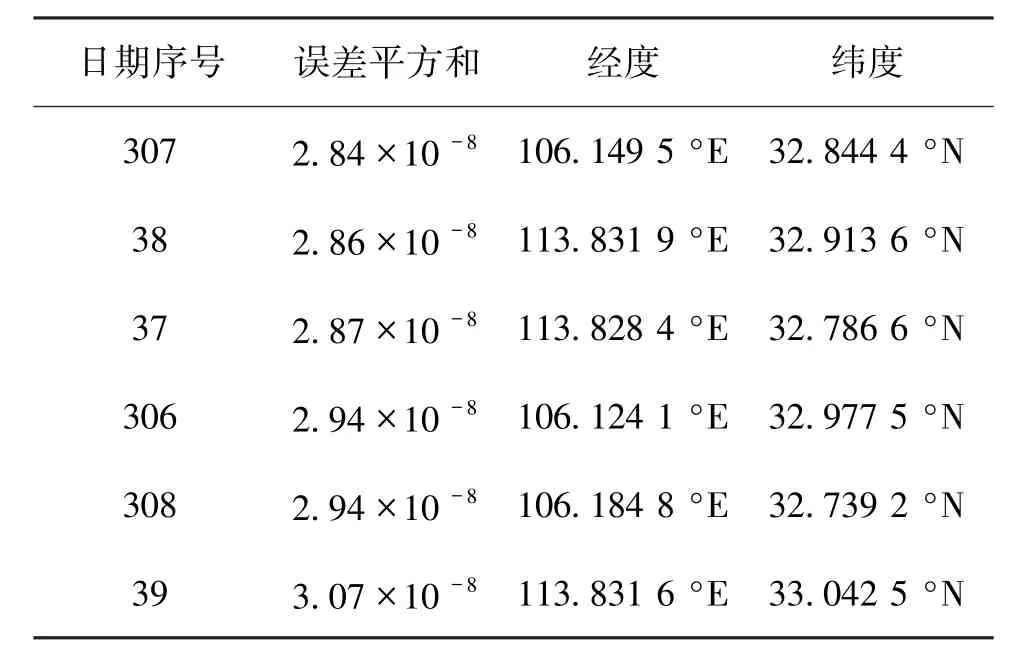
表2 附件3计算出的前6个候选日期序号及相应经纬度

利用非线性规划模型式(8)计算的影长和测量影长如图7和图8所示。

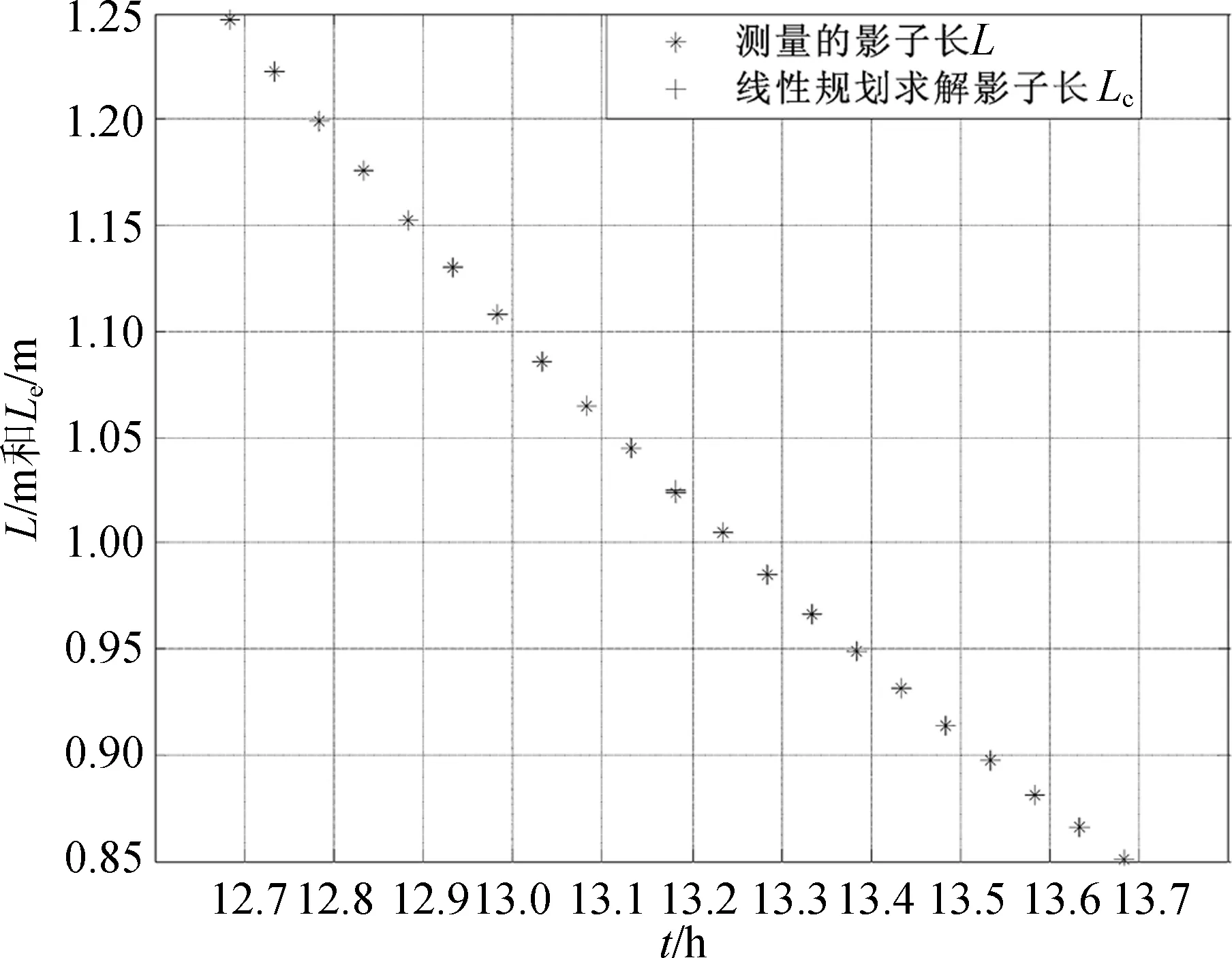
图7 附件2中n＝200测量影长和规划影长对比图

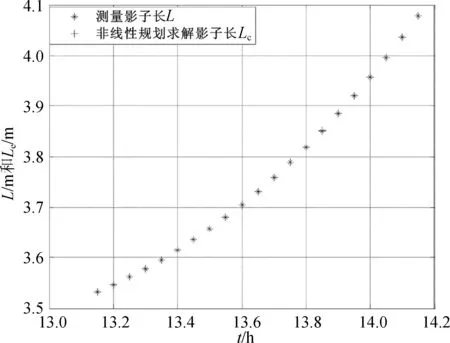
图8 附件3中n＝307测量影长和规划影长对比图

由表1和表2可知，附件2中直杆的可能地点为 (78.907 6°E，39.871 9°N)，日期为5月24日或 (81.239 2°E，39.939 2°N)，日期为 7 月 19日。附件3中直杆的可能地点为 (106.149 5°E，32.844 4°N)，日期为11月3日或 (113.829 5°E，32.904 7°N)，日期为2月7日。

3 监控视频定位模型

在实际应用中，需要根据直杆在太阳下的影子变化的视频，确定视频的拍摄地点和时间。

拍摄日期和时间可以从视频中直接得到，所以该问题的关键是如何从视频中提取直杆和影子的位置及影子顶点坐标等信息，从而将该问题转化为第2节中讨论的问题，然后利用已建立的模型进行求解，得到视频拍摄的可能地点。

首先，对视频进行图像二值化处理。利用MATLAB按固定频率取各帧图像，将图像进行灰度、归一化及二值化处理[11]，过滤掉不需要的背景部分，使包含影子的目标区域更为明显，如图9和图10所示。

图9 灰度化处理图

图10 二值化处理图

其次，通过边缘检测方法[12]提取影子。为处理方便，裁剪掉上方复杂部分，保留下方1/3部分，如图11所示。

图11 影子区域水平线检测示意图

其中红色矩形框为要检测的影子区域。取直杆的脚点为原点，从原点开始从左向右进行竖直方向的扫描线检测，找到影子的顶点。

再次计算影子长度，得到影子顶点坐标。由于所给视频的影子是经过相机的中心投影形成的，而且是从三维的世界坐标系映射到了二维的设备坐标系，所以要想准确计算影子长度与杆的比例，必须进行透视处理，做坐标转换，求出相机的校准矩阵[5，11]。

最后，利用第2节中建立的非线性规划模型式(8)，在已知拍摄时间的情况下，得到拍摄地点为(115.248 7°E，40.142 5°N)，在缺失拍摄时间的情况下，得到拍摄地点为 (110.147 2°E，41.687 6°N)。

由模型计算的影子长度和实际测量影子长度高度吻合，模拟效果良好，如图12所示。

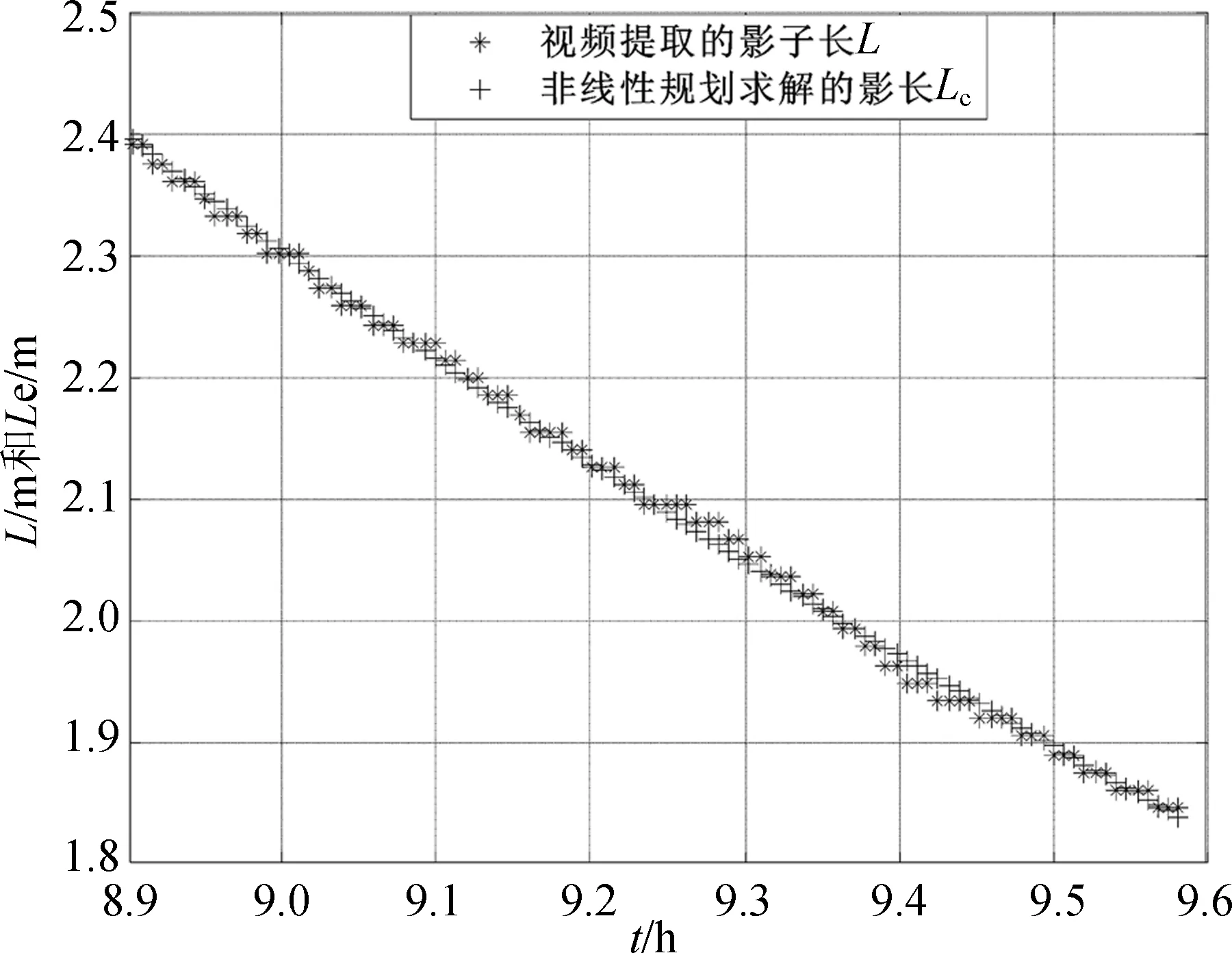
图12 视频提取影长与计算影长对比图

4 结束语

本文将直杆在阳光下产生的影子轨迹近似代替太阳运动的轨迹，将太阳绕地球的旋转轨道近似为圆形，确定了太阳影子长度随日期、时间、直杆位置及长度等参数的变化规律；然后利用非线性规划模型，求出了拍摄时间和拍摄地点。采用曲线拟合的方法确定非线性规划的初值，提高了精度，并通过实际数据的检验，得到较合理的结果。在模型求解过程中如果利用遗传算法、粒子群算法等智能算法将会进一步减少误差，这是今后研究的内容。

[1]全国大学生数学建模竞赛组委会.2015年高教社杯全国大学生数学建模竞赛[EB/OL]. [2015－12－15].http://www.mcm.edu.cn/html＿cn/block/c61dfec317 d7a5bd9b2b8efed81c8af3.html.

[2]百度百科.赤纬角[EB/OL].[2015－12－15].http://baike.baidu.com/link？ url＝ xAO9Hmxqeo8I4－1gkHkrc NfobhF2PnLeVa5SkOxldcIFJ＿Nsz－giDraluaghm Gamt E0NSExTbxrL2＿pO162B1K＆qq－pf－to ＝pcqq.c2c.

[3]百度百科.太阳高度角 [EB/OL].[2015－12－15].http://baike.baidu.com/view/86609.htm.

[4]百度百科.太阳方位角 [EB/OL].[2015－12－15].http://baike.baidu.com/view/862818.htm.

[5]武琳.基于太阳阴影轨迹的经纬度估计技术研究[D].天津:天津大学，2010.

[6]单黎明.太阳跟踪定位技术及其应用研究[J].空间控制技术与应用，2012，38(3):58－62.

[7]韩中庚.数学建模方法及其应用[M].北京:高等教育出版社，2009.

[8]司守奎，孙玺菁.数学建模算法与应用[M].北京:国防工业出版社，2011.

[9] 维基百科.真太阳时[EB/OL].[2015－12－15].https://en.wikipedia.org/wiki/Solar＿time＃Apparent＿ solar＿time.

[10]汪晓银，邹庭荣，周保平.数学软件与数学实验[M].北京:科学出版社，2010.

[11]RAFAEL C，GONZALE Z，RICHARD E.数字图像处理[M].北京:电子工业出版社，2002.

[12]黄楠.改进的数学形态学图像边缘提取算法研究[J].计算机仿真，2012，29(3):288－291.