基于混合分布的轮式装载机半轴载荷谱编制

翟新婷，张晓晨，江柱锦，李莺莺，张 强，王继新※

（1. 吉林大学机械科学与工程学院，长春 130025；2. 天津工程机械研究院，天津 300384；3. 广西柳工机械股份有限公司，柳州 545000）

0 引 言

载荷谱是零部件疲劳分析的基础[1-3]。由于载荷谱测试耗时耗力，只能通过外推的方法将有限时间内的测试载荷谱外推至全寿命周期载荷谱[4-5]。传统的载荷谱编制方法采用雨流计数[6-7]对测得的载荷-时间历程进行处理，得到均、幅值载荷及其循环频次，进行频次外推和合成等统计学处理。

在编制过程中，通常采用正态分布对均值载荷及其作业频次进行拟合，威布尔分布对幅值载荷及其作业频次进行拟合。基于上述单分布，陈东升等[8]建立了军用车辆传动系零件载荷谱；刘永臣等[9]建立了装载机传动系载荷谱；张英爽等[10]建立了工程车辆传动系后法兰载荷谱；高云凯等[11]提出了简化加速车身台架疲劳试验程序载荷谱的编谱方法。上述文献中的载荷数据均通过对应分布的拟合检验，对具有单峰载荷特征的载荷谱编制具有重要意义。而农用拖拉机、装载机等非道路车辆的作业工况是复杂多变的，导致其承受的载荷随机多变，并呈现单峰、多峰等形式。基于单分布的载荷谱编制时，当载荷呈单峰分布时，可能存在拟合检验不通过的现象；而呈多峰分布时，很难充分反映多峰分布的特征，影响载荷数据的拟合效果，上述问题的存在直接影响载荷的外推和合成。为解决上述问题，获得更加符合实际作业工况的载荷谱，其关键在于载荷分布的确定。混合分布具备多个分布组合的优势，能够有效提升载荷分布的拟合效果，从而弥补单分布拟合上的不足。

本文以轮式装载机为例，研究其测试及作业段划分方法，在传统编制方法的基础上提出一种基于混合分布的载荷谱编制方法，可为疲劳设计提供数据参考。

1 函数拟合模型介绍

假设混合总体的样本来自 c个不同统计特性的分布函数，则其概率密度函数表达式为[12-13]

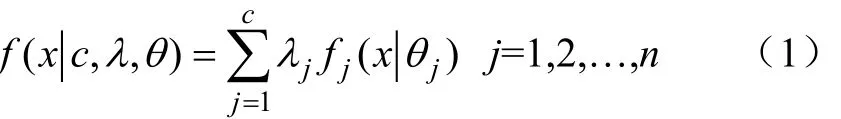
式中 f(x|c,λ,θ)为混合概率密度函数；fj(x|θj)为第 j个子分布函数的概率密度函数；c为子分布函数的个数；θ为各分布函数的参数集合；λj为各子分布函数的权重系数，且满足

对应的累积分布函数为：

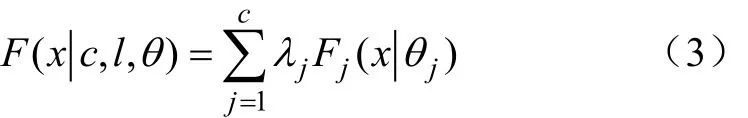
当c=1时，上述分布函数即为单分布函数的表达式。

2 测试半轴载荷数据分段

本试验选取 ZL50CN型轮式装载机，选定特性一致的石子为物料操作对象，采用“V”型作业模式，每一斗的工作循环由“空载前进”、“铲掘”、“满载后退”、“满载前进”、“卸料”、“空载倒退”6个作业段组成[14]，如图1所示，装载机的行走路线呈“V”型。此外，在作业过程中，尽量保证料堆高度、宽度以及“V”型路线的统一。

图1 轮式装载机“V”型作业模式Fig.1 V-shaped operation modes of wheel loader

轮式装载机循环作业过程为非平稳随机过程，通常认为相同作业段满足平稳性假设[10]，因此，有必要对装载机的作业载荷进行作业段划分。装载机载荷作业段划分的关键是明确各作业段装载机的动作特征、确定相邻作业段之间的分界点。半轴是轮式装载机行走系统的重要组成部分，其疲劳失效影响整机的可靠性[15]。本文基于车速、铲斗缸位移数据，对半轴扭矩载荷进行作业段划分。由于装载机在V6、V1段之间，以及V3、V4段之间的转换是倒退-前进的动作，装载机行驶方向发生变化，车速表现为先减速再增速的变化过程，因此根据车速得到V6、V1和V3、V4的分界点。然后，依据铲斗缸位移变化数据对应得到V5段，这是因为执行V5段时，铲斗缸从最大位移处收缩至最小位移处。最后，由于装载机铲掘作业时所受载荷大且波动剧烈，因此将半轴扭矩波动较大且密集的数据段作为V2段。作业段划分示意图见图2。

根据作业段划分需求，确定半轴扭矩、铲斗缸位移及车速为待测数据，图3为待测件及数据采集系统。

试验中采用SoMat eDAQ多通道数据采集系统进行数据同步采集，采用BF350-5HA型应变片组成全桥电路，利用 285系列数码遥测系统的发射器与接收器共同作用实现半轴扭矩信号的发射和接收。针对油缸数据，通过HPS-L1-30-V5传感器测得位移数据。此次测试系统采用GPS定位实现装载机路径监控，从而得到装载机的行驶车速数据。考虑到装载机的作业模式和载荷特点，连续完成100个工作循环并进行试验数据记录。

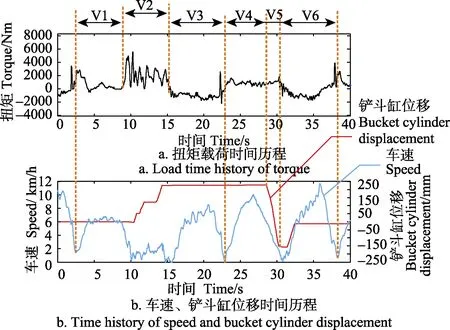
图2 作业段划分示意图Fig.2 Schematic of section division

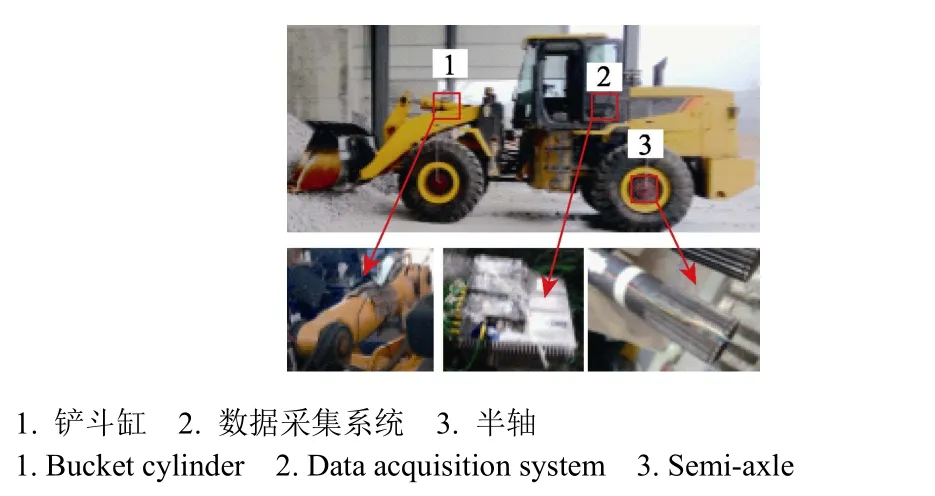
图3 待测件及数据采集系统Fig.3 Measured components and acquisition system

将测得的数据经过滤波、降噪处理。选用“db3”小波基函数，小波分解层数为 3，Penalty阈值对装载机的右后半轴扭矩载荷数据进行降噪处理[16-17]，图 4为处理后的扭矩数据。

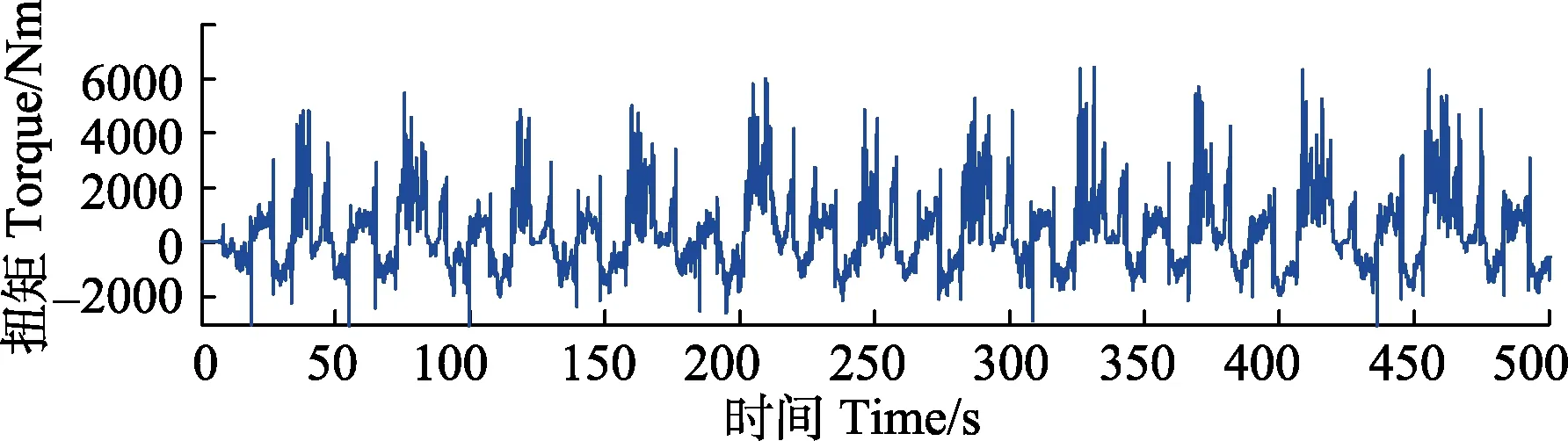
图4 滤波降噪后的扭矩数据Fig.4 Torque data after filtering and noise reduction

3 半轴实测载荷参数法外推

在测试过程中，测得的是扭矩信号，此处根据应力扭矩转换公式（4），将扭矩载荷转换为应力载荷

式中Wp=16为抗扭截面系数；ds=54 mm为半轴直径；M为半轴所受扭矩，Nm。

3.1 均幅值载荷独立性检验

将分段后的数据进行转折点提取，采用双参数雨流计数法，将数值小于随机载荷历程极差 10%的小载荷进行删除，得到载荷的均、幅值及其频次信息。

均、幅值载荷分布估计的目的是为了进行极值和频次外推。首先要对载荷的均、幅值的独立性进行检验[18]。根据 Fisher定理，若均、幅值相互独立，则服从自由度为(r-1)(s-1)的 χ2分布[11,19]，见式（5）。

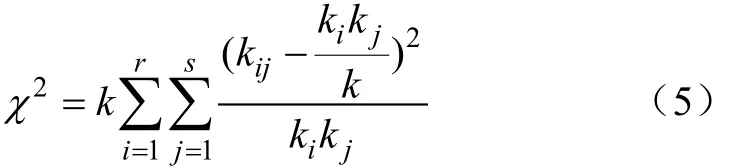
式中 k为各作业段样本长度；r、s为幅值和均值划分的等级数，构成s×r阶向量，即雨流矩阵向量；ki为幅值在第i级的频次数；kj为均值在第j级的频次数；kij为载荷循环落在第i级幅值，第j级均值的频次数。

根据 χ2分布性质可知，当自由度 m=(r-1)(s-1)＞45，该分布近似服从N(m，2m)的正态分布。因此，可根据式（6）近似得到χ2分布的上α分位点。

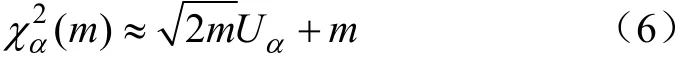
式中Uα查标准正态分布表。

本文对 6个作业段载荷的均、幅值均进行划分，按照以往经验划分为64级[20-22]。通过雨流计数得到64×64阶雨流矩阵，即r=64，s=64，χ2分布的自由度m=3 969，因此根据式（6）可近似得到该分布下的分位点(3969)=4 115.6。根据式（5）计算得到6个作业段χ2值均小于4115.6，因此可以认为在95%的置信度下6个作业段的均幅值相互独立。

因此，相互独立的条件下，均幅值载荷的联合分布函数即为二者各自分布函数的乘积。

3.2 均幅值载荷分布估计

以半轴铲掘段雨流计数数据为例，分别采用单分布和混合分布对均值和幅值载荷进行分布估计。混合分布一般由2个、3个或者多个分布组成，并且每一个子分布可由任何单一分布组成。但是当混合分布包含多个不同子分布时，对其子分布的未知参数进行估计就比较困难。因此，为简化求解过程并降低了参数估计难度，本文采用同类双分布。采用极大似然估计法（maximum likelihood estimation，MLE）进行单分布估计，最大期望（expectation maximum，EM）法进行混合分布估计[23-26]。MLE法和EM法都是基于似然函数最大化的原理进行的，且似然估计值越大，估计结果越好[27]。

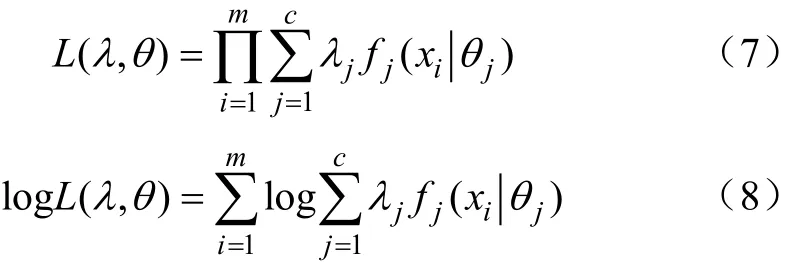
式（7）是混合模型的似然函数；为简化计算，对两边同时取对数，得到对数似然函数，见式（8）。

决定系数R2是从拟合精度的角度定量描述理论模型与对应的测试数据之间的差异[28]，且R2越接近1表明拟合效果越好，因此采用决定系数作为拟合检验指标。

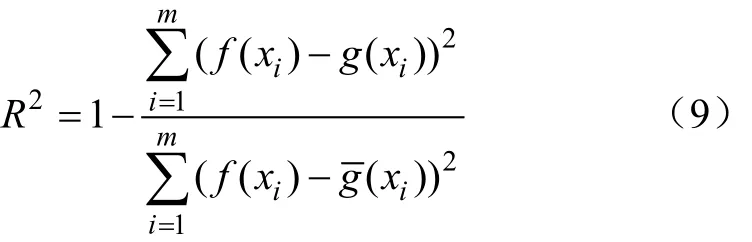
式中f(xi)是实测载荷的概率密度值，g(xi)为理论模型的概率密度值，( xi)为理论模型在所有采样点的概率平均值。

以V2段均值、幅值载荷以及V4段幅值载荷为例，基于参数估计值得到数据拟合直方图，将上述分析结果以曲线拟合的形式进行展示，如图5所示。

表 1为单双分布模型的参数估计值及其拟合效果检验值。其中V1、V2、V3、V5以及V6的均、幅值双分布的对数似然函数值均大于对应单分布的对数似然函数值，且均值双分布函数的 R2值比对应单分布函数的 R2值分别大32%、2.3%、25.1%、40.1%和160.8%，幅值双分布函数的R2值比对应单分布函数的R2值分别大8.3%、6.7%、1.4%、6.2%和1.2%。分析V4段数据，均值双分布的对数似然函数值以及R2（0.995 9）均大于单分布的对应值，而幅值双分布的对数似然函数值以及R（20.976 2）小于单分布的对应值，因此可知V4段均值采用双分布拟合效果较佳，幅值采用单分布拟合效果较佳。

3.3 二维外推载荷谱

实际载荷测试过程中，只能得到有限量的载荷数据。为了得到全寿命周期中可能出现的载荷历程，一般根据式（10）将载荷累积频次扩展到106次。

表1 各作业段参数估计结果Table 1 Parameter estimation results for each section

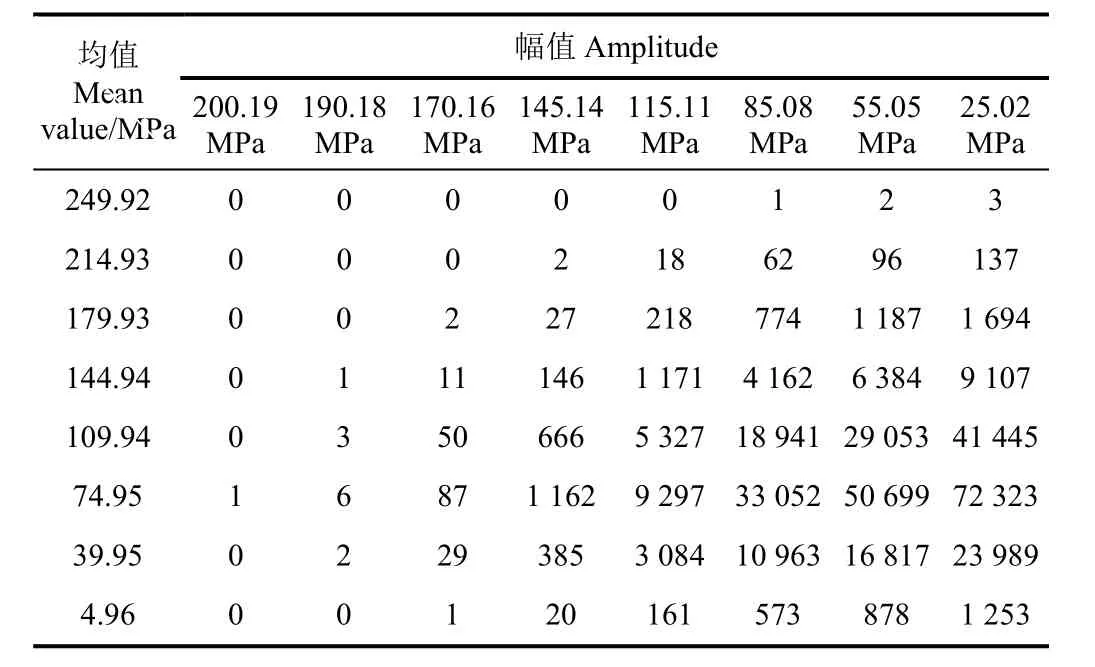
表2 V2段二维载荷谱Table 2 Two-dimensional load spectrum of V2

式中N为载荷总频次，Ni为某作业段的载荷频次，Ni'为扩展后的载荷频次。因此可知各作业段扩展后的频次数分别为：76 611、391 158、189 673、149 173、745 867和118 798。

由于各段均、幅值相互独立，且满足相应分布的拟合要求，因此求载荷的极值可转化为求均值、幅值分布函数的最大值。拟合检验值决定了载荷分布函数估计值的准确性，根据3.2节的参数估计结果，以较大的R2值作为选取标准，V1、V2、V3、V5以及V6段的均、幅值分布采用双分布，V4段均值采用双分布，幅值采用单分布。根据各段选定的载荷分布函数以及极值发生概率P(1/总频次)，见式（11），计算均、幅值的极值。

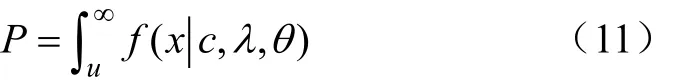
式中u即为P概率对应的极大值。

根据均值、幅值的极大值，用等间隔法对均值进行划分，不等间隔法对幅值进行划分，各分为 8级[11]。根据选定的均、幅值分布函数建立联合概率密度函数，从而得到对应均值、幅值载荷的循环频次，形成二维载荷谱，以V2段为例得到其二维载荷谱，见表2。

3.4 生成一维程序谱

二维载荷谱是关于均、幅值载荷及其作业频次的谱，在实际台架试验中，由于其均、幅值的变动使得加载过程繁琐，为简化操作，通常采用一维程序谱[7,9-11]，即均值固定，幅值变动的方式，因此本文根据Goodman原理[29]将二维载荷谱进行转换处理，使其转换为均值为 0的一维程序谱。

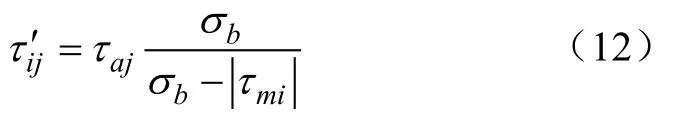
式中 τij'为等效应力幅值，MPa；τaj为第 j个应力幅值，MPa；τmi为第i个应力均值，MPa；σb为材料强度极限，MPa，本文半轴材料为20CrMnTi，σb=1 080 MPa。

转换后得到64×2阶的等效应力幅值-频次(Si-ni)的矩阵，将等效应力幅值的最大值作为最大目标幅值，根据不等间隔法对其进行划分，得到8级目标幅值。

基于Miner疲劳累积损伤理论[30]，总损伤D=Deq，以及材料的S-N曲线关系可得一维程序谱的加载频次。

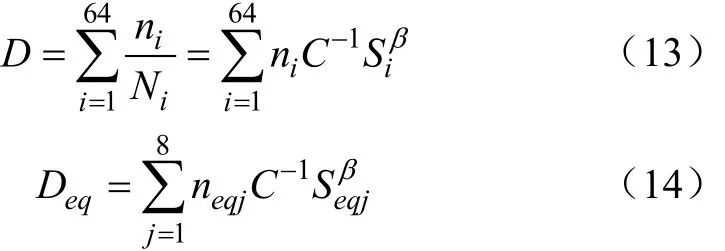
式中Si为等效幅值，MPa；ni为Si对应频次；Seqj为8级目标幅值，MPa；neqj为 Seqj对应的频次；C为材料性质常数。

根据所选材料，在 95%可靠度下，参数 β取值为21.886 6[31]。从而得到各作业段的一维程序谱，见表3。

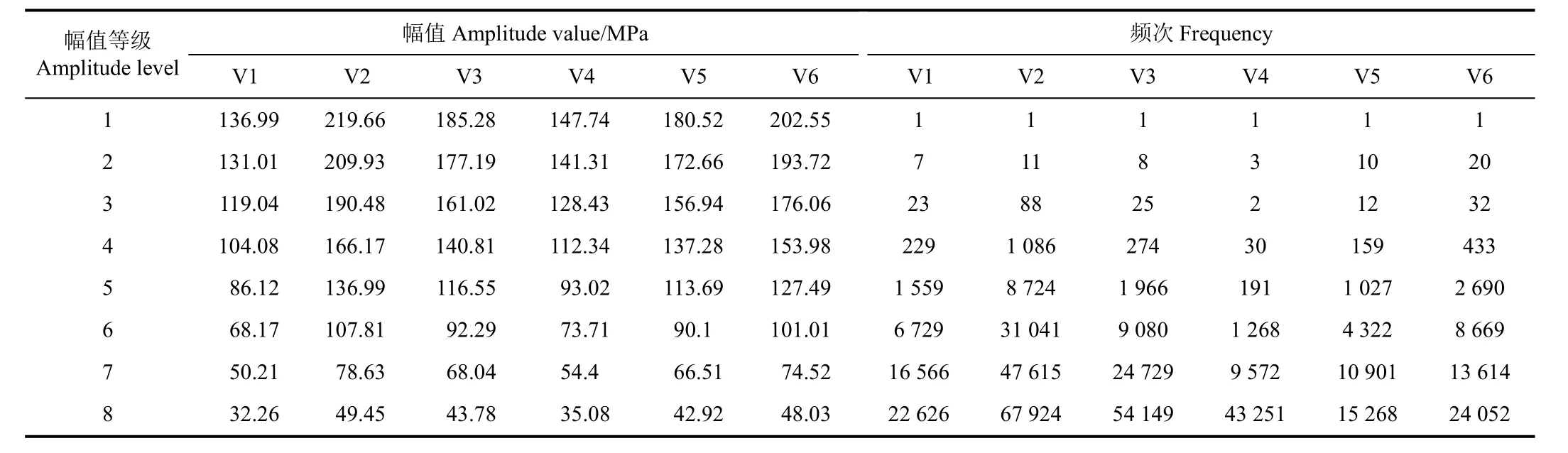
表3 半轴载荷各作业段一维程序谱Table 3 One-dimensional program loading spectrum of semi-axle load in six sections

4 结 论

1）根据装载机“V”型作业模式，结合装载机的动作特征，确定作业段划分方法，实现了测试载荷的 6作业段划分，满足载荷平稳性要求。

2）利用雨流计数法，得到64×64阶的雨流矩阵，结合下分位点数值4 115.6，可知在95%的置信度下6个作业段的均值、幅值相互独立。

3）分别采用单分布和混合分布对均值、幅值载荷进行拟合，对比结果具体表现为：V1，V2，V3，V5和V6段均值双分布函数的R2值比对应单分布函数的R2值分别大32%、2.3%、25.1%、40.1%和160.8%，幅值双分布函数的R2值比对应单分布函数的R2值分别大8.3%、6.7%、1.4%、6.2%和 1.2%。V4段幅值单分布函数的 R2值为0.995 9，该值大于对应混合分布函数的R2值0.962 2。

4）提出基于混合分布的载荷谱编制方法，选取拟合较优的分布，即V1，V2，V3，V5和V6段均值、幅值以及 V4段均值采用混合分布，V4段幅值采用参数为（8.717 1，0.887 1，9.344 1）的威布尔分布，从而实现频次的合理外推和合成，得到一维程序载荷谱。

[参 考 文 献]

[1] Heuler P, Klätschke H. Generation and use of standardised load spectra and load–time histories[J]. International Journal of Fatigue, 2005, 27(8): 974－990.

[2] Wang J, Zhai X, Liu C, et al. Determination of the threshold for extreme load extrapolation based on multi-criteria decision-making technology[J]. Strojniški vestnik-Journal of Mechanical Engineering, 2017, 63(3): 201－211.

[3] Pokorný P, Hutař P, Náhlík L. Residual fatigue lifetime estimation of railway axles for various loading spectra[J].Theoretical & Applied Fracture Mechanics, 2016, 82: 25－32.

[4] 李凡松, 邬平波, 曾 京. 基于核密度估计法的载荷历程外推研究[J]. 铁道学报, 2017, 39(7): 25－31.Li Fansong, Wu Pingbo, Zeng Jing. Extrapolation of load histories based on kernel density method[J]. Journal of the China Railway Society, 2017, 39(7): 25－31. (in Chinese with English abstract)

[5] Johannesson P. Extrapolation of load histories and spectra[J].Fatigue & Fracture of Engineering Materials & Structures,2006, 29(3): 209－217.

[6] 李 雯, 张承宁, 宋 强,等. 混合动力汽车电机驱动系统二维载荷谱研究[J]. 农业机械学报, 2010, 41(7): 21－24.Li Wen, Zhang Chengning, Song Qiang, et al. 2D load spectrum for motor propulsion system on hybrid electric vehicle[J]. Transactions of the Chinese Society for Agricultural Machinery, 2010, 41(7): 77－80. (in Chinese with English abstract)

[7] 李凡松, 邬平波, 曾 京. 车下设备承载结构疲劳试验载荷谱编制方法[J]. 机械工程学报, 2016, 52(24): 99－106.Li Fansong, Wu Pingbo, Zeng Jing. Compilation method of fatigue test load spectrum for underfloor equipment bearing structure[J]. Journal of Mechanical Engineering, 2016, 52(24):99－106. (in Chinese with English abstract)

[8] 陈东升, 项昌乐, 陈 欣. 军用车辆传动系零件载荷谱的建立[J]. 机械强度, 2002, 24(2): 310－314.Chen Dongsheng, Xiang Changle, Chen Xin. Establishment of the spectrum of the military vehicle transmission elements[J]. Journal of Mechanical Strength, 2002, 24(2):310－314. (in Chinese with English abstract)

[9] 刘永臣, 常 绿, 孙 丽. 轮式装载机传动系载荷谱编制方法研究[J]. 中国机械工程, 2012, 23(12): 1412－1416.Liu YongChen, Chang Lǜ, Sun Li. A method of compiling load spectrum on wheel loader transmission[J]. China Mechanical Engineering, 2012, 23(12): 1412－1416. (in Chinese with English abstract)

[10] 张英爽, 王国强, 王继新,等. 工程车辆传动系载荷谱编制方法[J]. 农业工程学报, 2011, 27(4): 179－183.Zhang Yingshuang, Wang Guoqiang, Wang Jixin, et al.Compilation method of power train load spectrum of engineering vehicle [J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE),2011, 27(4): 179－183. (in Chinese with English abstract)

[11] 高云凯, 徐成民, 方剑光. 车身台架疲劳试验程序载荷谱研究[J]. 机械工程学报, 2014, 50(4): 92－98.Gao Yunkai, Xu Chengmin, Fang Jianguang. Study on the programed load spectrum of the body fatigue bench test[J].Journal of Mechanical Engineering, 2014, 50(4): 92－98. (in Chinese with English abstract)

[12] Timm D H, Tisdale S M, Turochy R E. Axle load spectra characterization by mixed distribution modeling[J]. Journal of Transportation Engineering, 2005, 131(2): 83－88.

[13] 傅大宝, 叶肖伟, 倪一清,等. 基于遗传算法和有限混合分布的应力谱多模态建模[J]. 工程力学, 2014, 31(5): 172－179.Fu Dabao, Ye Xiaowei, Ni Yiqing, et al. Multi-modal modeling of stress spectrum using genetic algorithm and finite mixture distributions[J]. Engineering Mechanics, 2014,31(5): 172－179. (in Chinese with English abstract)

[14] 王继新, 季景方, 胡际勇,等. 基于贝叶斯理论的工程车辆载荷样本长度计算方法[J]. 农业工程学报, 2011, 27(6):148－151.Wang Jixin, Ji Jingfang, Hu Jiyong, et al. Bayesian method for determination of load sample size in engineering vehicles[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2011,27(6): 148－151. (in Chinese with English abstract)

[15] 张英爽, 王国强, 王继新,等. 轮式装载机半轴载荷谱编制及疲劳寿命预测[J]. 吉林大学学报：工学版, 2011, 41(6):1646－1651.Zhang Yingshuang, Wang Guoqiang, Wang Jixin, et al. Load spectrum compiling and fatigue life prediction of wheel loader axle shaft[J]. Journal of Jilin University: Engineering and Technology Edition, 2011, 41(6): 1646－1651. (in Chinese with English abstract)

[16] 陈鸿彬. 挖掘机液压系统压力载荷谱编制方法研究[D].长春：吉林大学，2017.Chen Hongbin. Research on the Load Spectrum Compiling of the Pressure in the Hydraulic System of an Excavator[D].Changchun: Jilin University, 2017. (in Chinese with English abstract)

[17] 王继新, 季景方, 张英爽,等. 基于小波分形理论的工程车辆时域载荷信号降噪方法[J]. 吉林大学学报：工学版,2011(s2): 221－225.Wang Jixin, Ji Jingfang, Zhang Yingshuang, et al. Denoising method of time domain load signals of engineering vehicles based on wavelet and fractal theory[J]. Journal of Jilin University: Engineering and Technology Edition, 2011, (s2):221－225. (in Chinese with English abstract)

[18] 贾海波. 轮式装载机传动系载荷谱测试与编制方法研究[D].长春：吉林大学，2009.Jia Haibo. Study on the Test and Generation Methods about Load Spectrum of Wheel Loader Driveline[D]. Changchun:Jilin University, 2009. (in Chinese with English abstract)

[19] 成 凯, 张 盾. 推土机车架纵梁程序加载载荷谱的编制[J].农业工程学报, 1997, 13(4): 40－45.Cheng Kai, Zhang Dun. The program of load spectrum applying on lengthwise beam of dozer frame[J]. Transactions of the Chinese Society of Agricultural Engineering(Transactions of the CSAE), 1997, 13(4): 40－45. (in Chinese with English abstract)

[20] Johannesson P, Speckert M, Dressler K, et al. Guide to load analysis for durability in vehicle engineering[M]. John Wiley& Sons Inc, 2013: 40－48.

[21] 张英爽. 装载机传动系载荷谱的测取与应用研究[D]. 长春：吉林大学，2014.Zhang Yingshuang. Research on the Load Spectra Acquisition and Application of Loader Driveline[D].Changchun: Jilin University, 2014. (in Chinese with English abstract)

[22] 刘永臣, 王国林, 孙丽. 车辆控制臂疲劳损伤分析与寿命预测[J]. 农业工程学报, 2013, 29(16): 83－91.Liu Yongchen, Wang Guolin, Sun Li. Fatigue damage analysis and life prediction for vehicle control arm[J].Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2013, 29(16): 83－91. (in Chinese with English abstract)

[23] Bučar T, Nagode M, Fajdiga M. Reliability approximation using finite Weibull mixture distributions[J]. Reliability Engineering & System Safety, 2004, 84(3): 241－251.

[24] Ni Y Q, Ye X W, Ko J M. Modeling of stress spectrum using long-term monitoring data and finite mixture distributions [J].Journal of Engineering Mechanics, 2011, 138(2): 175－183.

[25] Wang J, Wang Z, Yang C, et al. Optimization of the number of components in the mixed model using multi-criteria decision-making[J]. Applied Mathematical Modelling, 2012,36(9): 4227－4240.

[26] Yang Z, Chen C, Wang J, et al. Reliability assessment of CNC machining center based on Weibull neural network [J].Mathematical Problems in Engineering, 2015, 2015(4):1－8.

[27] Shin J Y, Heo J H, Jeong C, et al. Meta-heuristic maximum likelihood parameter estimation of the mixture normal distribution for hydro-meteorological variables[J]. Stochastic Environmental Research & Risk Assessment, 2014, 28(2):347－358.

[28] Akdağ S A, Bagiorgas H S, Mihalakakou G. Use of two-component Weibull mixtures in the analysis of wind speed in the Eastern Mediterranean[J]. Applied Energy, 2010,87(8): 2566－2573.

[29] 徐灏. 疲劳强度[M]. 高等教育出版社, 1988: 233－243.

[30] 郭虎, 陈文华, 樊晓燕,等. 汽车试验场可靠性试验强化系数的研究[J]. 机械工程学报, 2004, 40(10): 73－76.Guo Hu, Chen Wenhua, Fan Xiaoyan, et al. Reasearch of enhancement coefficient of automobile reliability enhancement test on proving ground[J]. Journal of Mechanical Engineering, 2004, 40(10): 73－76. (in Chinese with English abstract)

[31] 安宗文, 高建雄, 刘 波. 基于P-S-N曲线的强度退化随机模型[J]. 计算力学学报, 2015, 32(1): 118－122.An Zongwen, Gao Jianxiong, Liu Bo. Stochastic model of strength degradation based on P-S-N curves[J]. Chinese Journal of Computational Mechanical, 2015, 32(1): 118－122. (in Chinese with English abstract)