振动方式和频率对杏树振动采收响应的影响

散 鋆 龙，杨会民，王学农，牛长河，郭文松，侯书林※

（1. 中国农业大学工学院，北京 100083；2. 新疆农业科学院农业机械化研究所，乌鲁木齐 830091）

0 引 言

杏（Armeniaca vulgaris）是具有高营养价值和经济价值的特色林果。目前中国杏采收仍为人工手摘或长杆敲打后捡拾等方式，采收成本占整个生产成本的 50%～70%[1-2]。新疆是中国主要的杏生产种植加工及出口地区，随着收获成本不断上涨，杏规模化、产业化发展受到了严重制约。林果机械化收获是提高采收效率、降低劳动成本的有效途径之一[3]。中国对林果机械化收获的研究起步较晚，理论研究不完善，迫切需要对林果机械化收获基础理论进行研究与探讨。

振动采收是林果机械化收获过程中应用最广泛的技术之一。早在1940年美国就已经开始了对林果机械化的研究，国外对林果振动收获理论进行了较为全面的分析和探讨[4]。Fridley等[5]等将果枝简化为悬臂梁模型进行研究，将果枝与振动机械视为单自由度振动系统进行分析；Whitney等[6-7]推导了果树与振动收获机间的受力及运动模型；Horvath等[8-9]将果树细分为三个部分：根系-土壤、树干-主枝和树冠，分析研究不同部分对整体振动系统的影响；Láng等[10-12]对樱桃树振动收获过程中果树能量损耗以及果树模型进行了研究；Bentaher等[13]建立了“Chemlali”品种橄榄树有限元模型，模拟规则振动激励与复合振动激励下果树振动收获过程，对两种收获方式下橄榄树的动态响应特性进行了分析和比较。

中国对林果机械化收获理论也进行了大量的研究。Du等[14-17]对修剪规则的樱桃树在不同的振动激励下的响应动态进行了研究，同时还研究了三维激振载荷对果树的激振作用，建立了果树有限元模型；蔡菲等[18-23]利用高速摄像仪分析果实受振动脱落过程的运动状态，此后对“Y”型果树动力学模型进行了仿真分析与试验。

本文主要通过研究杏树受到不同振动激励后的响应状态，分析杏树不同位置的振动响应，获得杏树不同位置受迫振动稳态后的加速度曲线、函数以及频谱图，研究最佳的杏树振动采收频率，为杏及其他品种林果的收获机械参数设计提供理论依据。

1 林果振动采收机结构与工作原理

1.1 振动采收机结构

常见的偏心振动式林果采收机偏心部件可分为单偏心和对称双偏心两种形式。本文选用两种机型来完成整个杏树受迫振动试验，单偏心式采收机选用新疆农垦科学院机械装备研究所4YS-24型偏心式林果收获机[24-26]，对称双偏心式采收机选用新疆农业科学院农业机械化研究所4GZG-25型牵引式林果振动收获机[27]。

1.2 工作原理

拖拉机后输出轴为振动采收机提供动力，工作机构由液压系统控制，液压油缸控制振动夹持机构位置与夹钳开合状态，液压马达带动偏心块旋转，为采收机提供稳定振动源。振动收获过程中，调整振动采收机夹钳位置，使其与果树树干夹紧，采收机与果树间刚性连接，偏心块转动产生激振力传递给果树，果树受迫产生振动。振动能量沿果树树干传递给果实，果实由于自身惯性作用产生加速运动，当果实产生的惯性力大于果实与果柄间连接力时，果实从果枝上脱离，完成整个采收过程。

2 主要结构与模型

2.1 振动采收机关键部件

偏心块是振动采收机的核心部件，不同的偏心块转动速度、转动方向、转动角度、质量与形状等可产生不同的正弦激振力[28]。4YS-24型偏心式收获机偏心块采用扇形设计，安装在夹持机构后方与夹持机构整合在一起悬挂在伸缩支臂上（如图 1a）；4GZG-25 牵引式振动收获机偏心块采用半圆形设计，2个偏心块对称安装在振动箱中，振动箱安装在夹持悬臂后方（如图1b），工作时偏心块同时转动，方向相反，速度相同。

图1 2种振动采收机偏心部件Fig.1 Two kinds of vibration harvesting machine eccentric parts

2.2 杏树受迫振动动力学模型

通过建立杏树受迫振动响应模型，分析在采收过程中杏树的连续振动响应状态与振动规律；建立杏树-采收机整体动力学模型，分析系统整体简谐振动的响应，明确杏树振动采收机理。

振动采收作业中，杏树与采收机组成连续的振动系统，为了便于分析与理论推导，将杏树简化为一端固定的悬臂梁结构[29]。此时，杏树可视为能够离散成有限个自由度的系统，树干视为等密度、等截面的圆柱梁，杏树树冠部分视为质量团，位于圆柱梁可活动端。经测量成熟期库麦提品种杏果实可溶性固形物含量为21.51%，杏树树干密度为0.76 g/cm3。根据国家标准[30-31]，测得杏树顺纹抗拉强度为 53.75 MPa，杏树树干含水率为38.39%。

在垂直平面上，以杏树根部中心o为原点，x方向为与地面垂直方向，y方向为水平方向，建立杏树平面坐标系，对杏树受迫振动进行动力学分析。

2.2.1 杏树受单偏心式振动模型

单偏心式收获机进行工作时，杏树受迫振动主要表现形式为扭转振动如图2所示。

图2 杏树扭转振动模型Fig.2 Torsional vibration model of apricot tree

树干受到扭转应力，针对圆形截面选用极惯性矩进行计算杏树转动惯量。因此杏树的转动惯量公式为

式中ω为扭振固有角频率，rad/s；待定常数A、B由边界条件决定，C、D由采收机振动输出初始条件决定。

由此可得杏树扭振的振型函数为

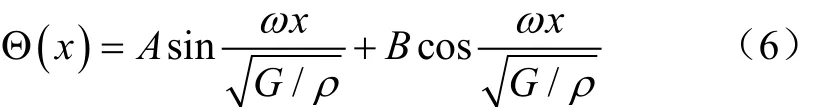
通过理论分析可知：杏树在单偏心振动过程中，以静止时中心轴做扭转运动，树干整体运动轨迹类似于倒圆锥体形，实际运动过程中由于树干和树枝具有一定的弹性，会出现一定的弯曲摆动现象。

2.2.2 杏树受对称双偏心式振动模型

对称双偏心式收获机进行工作时，杏树受迫振动主要表现形式为弯曲振动（如图 3），可将杏树视为典型的“欧拉-伯努利梁”，杏树被施加激振力后产生横向位移y(x，t)，长度为dx的杏树等截面单元受力如图3b所示。

图3 杏树横向振动模型Fig.3 Horizontal vibration model of apricot tree

根据牛顿第二定律可知，杏树单元体力矩平衡，简化后杏树符合欧拉-伯努利梁方程

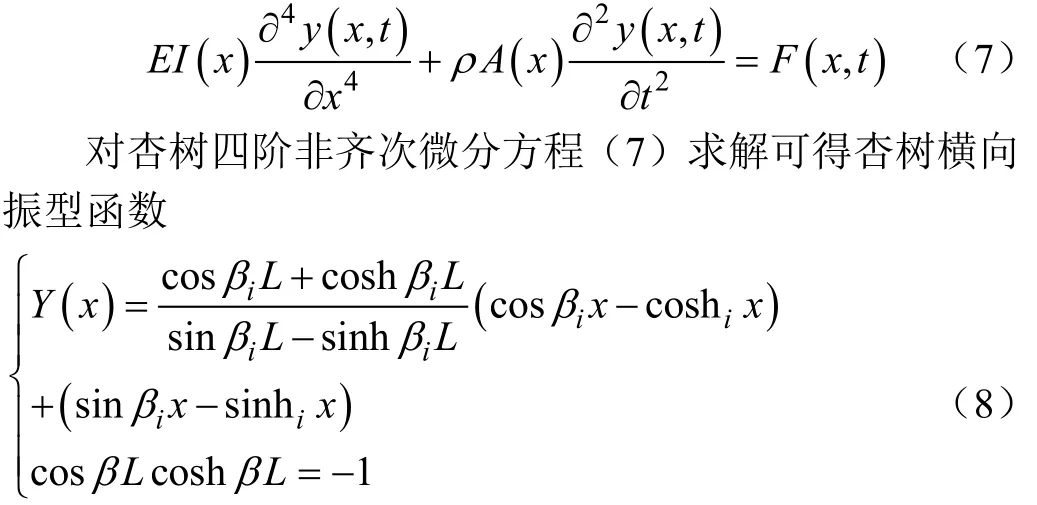
其中βi为式（7）微分方程的根；i取值为1，2，3，4。通过βi可计算果树i阶的固有频率。

理论分析表明：杏树受对称双偏心式采收机施加的振动激励时，沿着夹持位置方向做水平往复运动，树干整体运动轨迹类似于扇形。同样，受杏树自身材料特性影响，在运动过程中也会出现弯曲现象。

2.3 杏树-采收机动力学模型

在工作过程中，夹持机构与杏树刚性连接，可将杏树与采收机视为整体。在水平平面上，以杏树夹持位置中心o为原点的坐标系，x方向为振动系统水平运动方向，y方向为振动系统垂直运动方向，建立杏树-采收机动力学模型，如图4所示。利用等效弹性系数k与等效阻尼系数c表示杏树的力学特性，将杏树-采收机整体简化成为单自由度振动系统，采收机工作过程中，瞬时合力相互平衡，合力为0。

图4 杏树-振动采收机动力学模型Fig.4 Dynamic model of apricot tree -vibration harvester

对杏树-单偏心式采收机整体系统（如图4a）进行受力分析，建立系统在x与y方向上的振动微分方程组

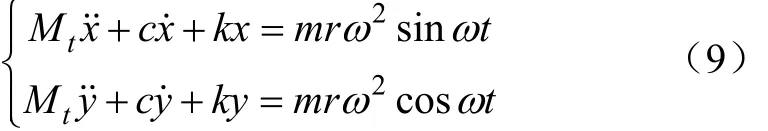
式中 Mt为采收系统总质量，kg；x为杏树偏离原点的 x方向位移，m；y为杏树偏离原点的y方向位移，m。

对称双偏心式采收机工作过程中，2个偏心块转速相同，方向相反，对杏树-对称双偏心式采收机振动系统（如图4b）受力分析可知：x方向上产生的偏心力大小相等，方向相同；y方向上产生的偏心力大小相等，方向相反，作用力相互抵消，合力为零。

系统振动微分方程为

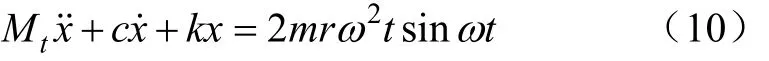
分别对 2个系统的二阶常系数微分方程进行求解，推导出系统振幅A与相位差θ表达式为

3 试验材料与方法

3.1 试验材料

本试验于2017年6月底杏成熟期，在新疆喀什地区莎 车 县 国 有 二 林 场 果 园 中 进 行 （ 38°12′24.54″N ，77°08′49.73″E），试验果园水肥管理良好，无套种作物，果树为8 a树龄的库买提杏树。

3.2 试验仪器

采收机：4YS-24型偏心式收获机和 4GZG-25 牵引式振动收获机。加速度传感器为苏州试验仪器设备公司：YMC压电式IEPE型加速度传感器，灵敏度50 mv/ms2，频率范围0～4 000 Hz，测试范围±10 g（g为重力加速度，取9.8 m/s2）。美国NI公司振动信号采集设备及软件：NI DAQ 9 178四通道信号采集器，NI 9 234振动信号采集卡以及LabView振动测试虚拟软件。

3.3 试验方法

在杏树主干夹持位置（一级枝干）以及沿主干向上每级树枝分叉的主枝干处安装传感器，每个传感器在竖直方向上间隔距离相等为800 mm。由于杏树分支受迫振动方向是不可预测的，为保证试验的准确性，所有传感器安装方向与夹持位置x方向传感器安装方向保持一致，传感器安装位置如图5所示。

图5 加速度传感器安装位置Fig.5 Installation location of acceleration sensor

为了测量夹持位置处杏树的响应状态是否与建立的杏树-采收机理论模型一致，按照模型坐标系在实际夹持位置x，y方向均安装传感器。

利用 2种振动采收装置进行振动试验，传感器通过传输线与NI DAQ 9 178振动信号采集仪相连，振动测试信号由LabView振动测试软件进行记录分析。杏树振动采收检测试验流程如图6所示。

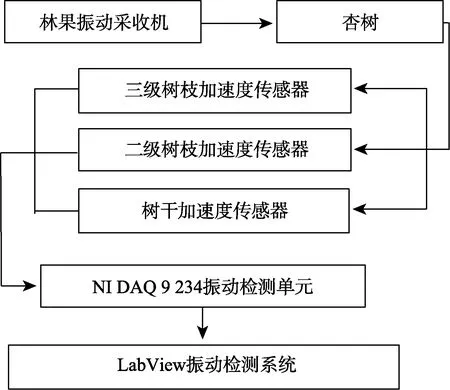
图6 振动检测技术路线图Fig.6 Technology roadmap of vibration detection

4 试验分析与结果

4.1 杏树-采收机动力学模型验证

根据杏树-采收机动力学模型微分方程求解所得系统振幅A，mm。单偏心式振动采收机x与y方向位移应满足

式中X为x方向位移，mm；Y为y方向上位移，mm.

由此可推导出杏树-单偏心式采收机系统振动轨迹为半径为A的圆形，其x与y方向加速度形成的图像也为圆形，半径为最大加速度值。通过对树干夹持位置 x，y方向安置传感器可得树干振动过程中的加速度李萨如图形，实际轨迹为绕圆心（0，0）的近似圆形轨迹。如图7a所示，实际轨迹与理论轨迹对比可知，树干实际振动过程与理论推导一致。

对称双偏心式振动采收机x方向位移：X2=A2；y方向位移：Y=0。可推导出振动过程中系统运动轨迹可视为沿夹持位置中心做往复直线运动。通过传感器测得加速度数据可知，实际运动位置集中在x为0的上下两侧区域。如图7b所示，实际轨迹与理论轨迹对比可知，实际杏树振动与理论推导一致。

4.2 杏树不同位置振动响应

为研究杏树振动过程中，振动响应与振动传递的过程，利用传感器测量不同位置杏树的振动时间差，将编写的LabView振动测试虚拟软件程序与NI DAQ 9 178四通道信号采集器得到的数据，导入MATLAB中并根据已推导公式进行拟合分析，得到不同位置杏树响应函数。

由于采集到的振动参数数据庞大，为了能更好研究和描述振动特性，本试验选取进入稳态后0.1 s内的数据，利用MATLAB曲线拟合分析工具进行分析。

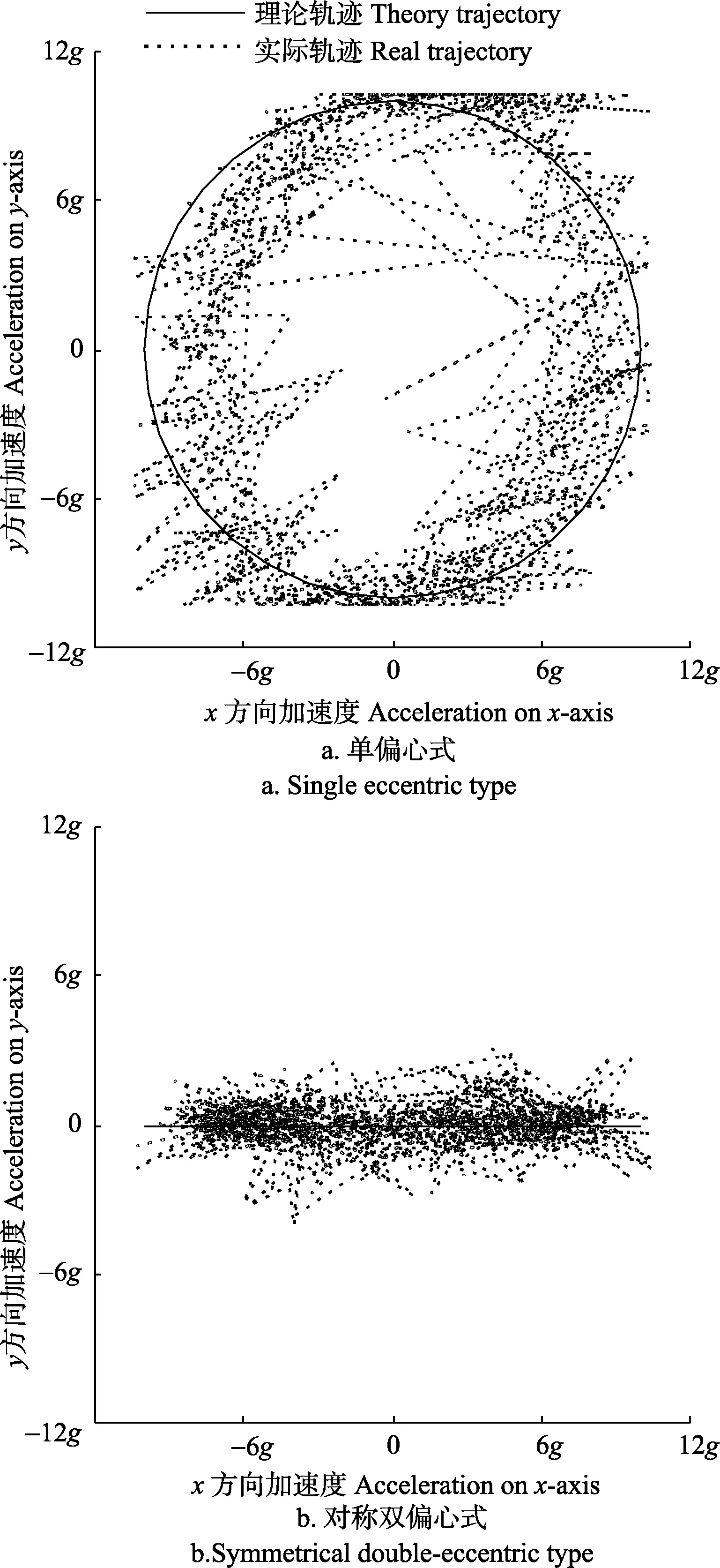
图7 2种振动采收机夹持位置加速度李萨如图形Fig.7 Clamping position Lissajous graphic of two kinds of vibration harvester

4.2.1 单偏心式振动收获杏树响应状态

单偏心式振动激励下杏树不同位置的振动响应曲线如图 8所示。由杏树振动模型可知，杏树受单偏心式振动过程中系统符合傅里叶变换形式，采用傅里叶拟合形式进行分析和求解。

振动激励进入稳态后，对0.85～0.95 s内杏树不同位置的振动数据进行拟合分析，拟合曲线如图9所示。

由振动响应曲线图8a可知，杏树夹持位置在0.135 s开始振动，0.259 s夹持位置达到稳态。稳态下夹持位置最大加速度为10.4 g，0.1 s内振动数据傅里叶拟合分析，可得R2为0.912 1。

单偏心式振动夹持位置加速度响应函数为

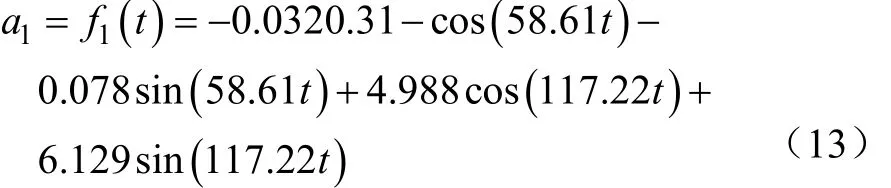
由图 8b可知，0.181 s时杏树二级枝干开始振动，0.282 s时二级枝干达到稳态，振动过程中最大加速度值为5.1 g。稳态下0.1 s内二级枝干振动数据傅里叶拟合分析，可得R2为0.928 6。

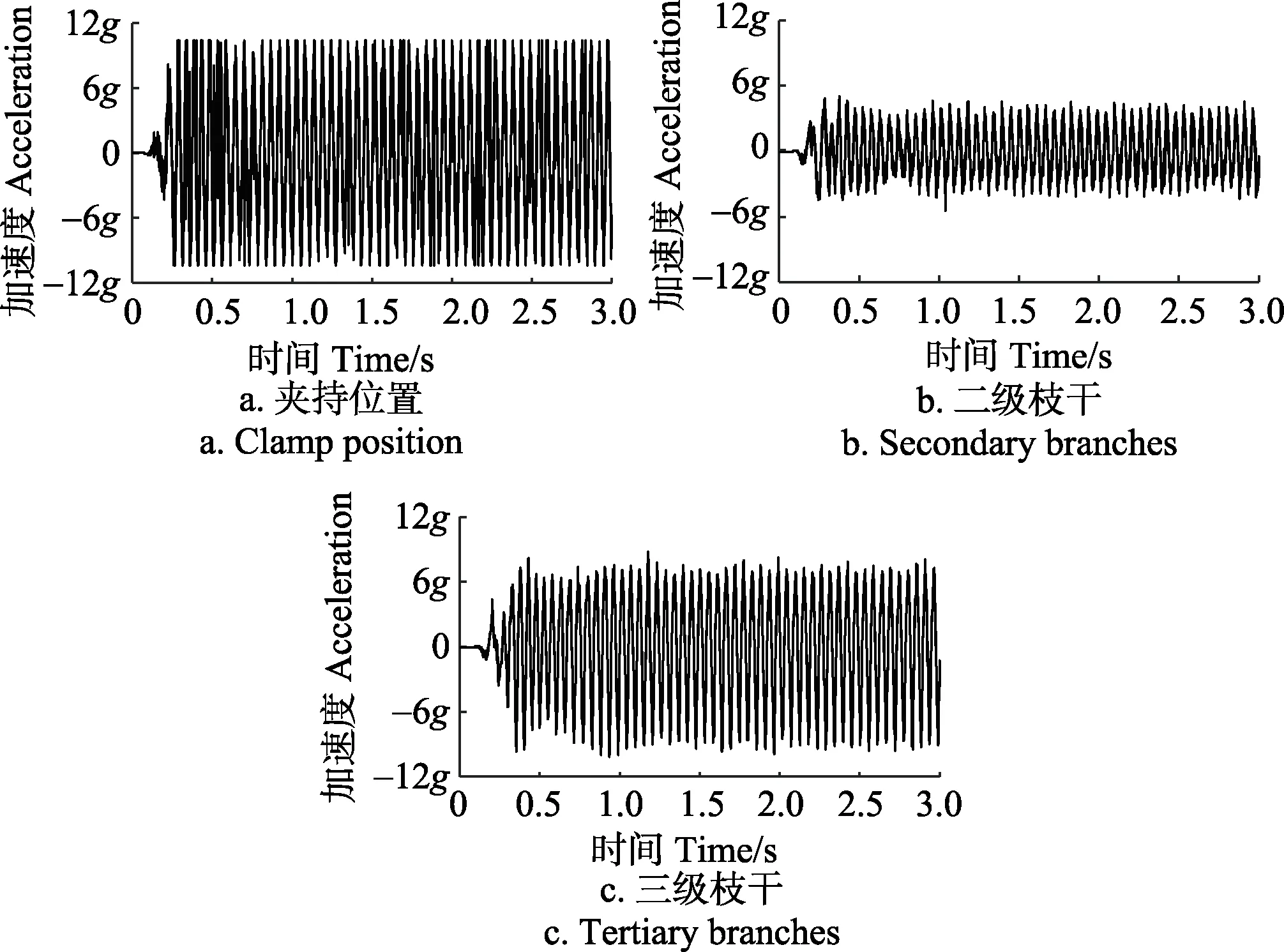
图8 单偏心式振动激励下杏树不同位置响应曲线Fig.8 Response curves of different locations of apricot trees by single eccentric vibration

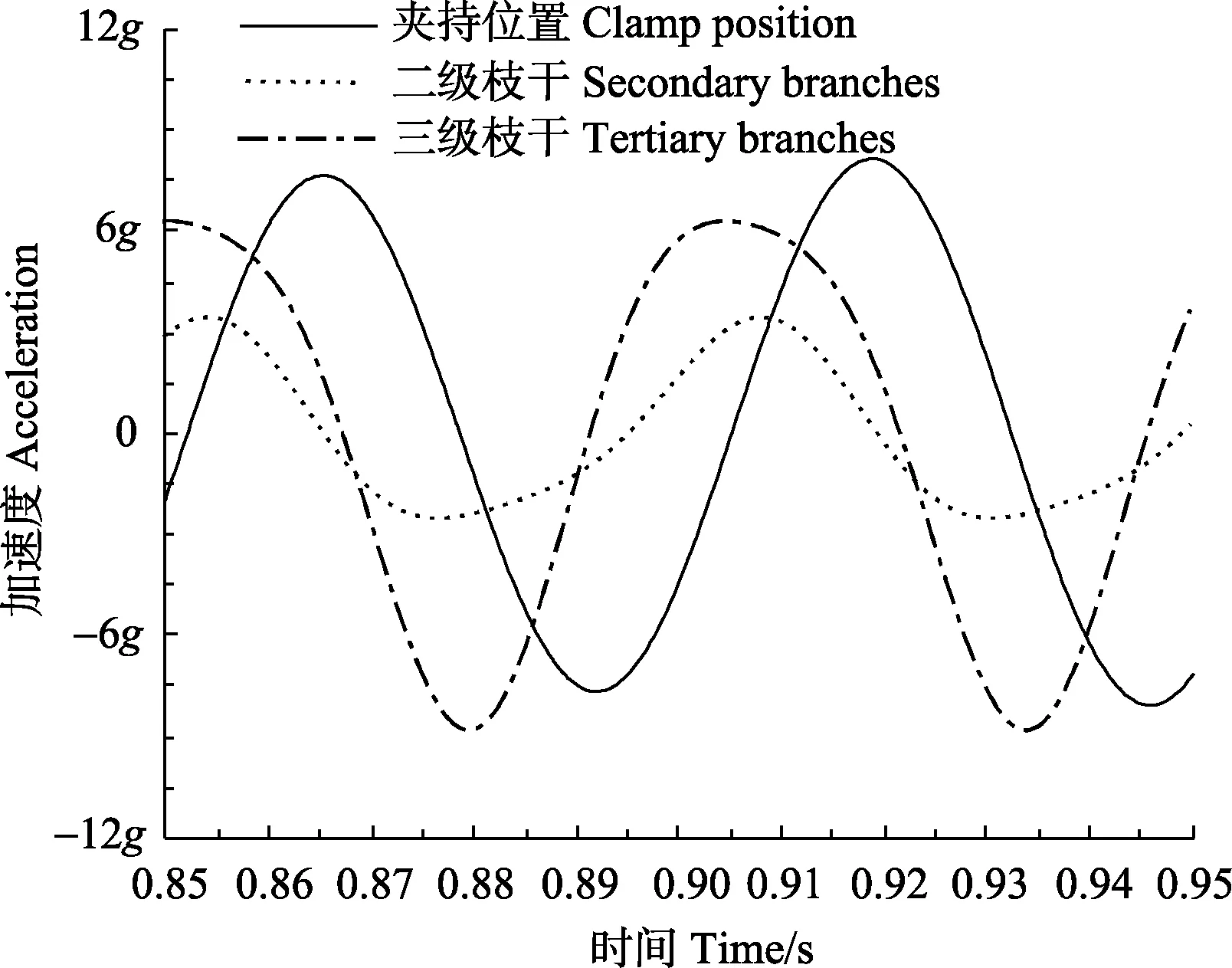
图9 单偏心式振动杏树不同位置加速度拟合曲线Fig.9 Fitted curve of acceleration of different locations of apricot trees by single eccentric vibration

单偏心式振动二级枝干加速度响应函数为

由图8c可知，杏树三级枝干在0.191 s时开始振动，0.351 s三级枝干达到稳态，最大加速度8.8 g。0.1 s内稳态振动数据傅里叶拟合分析，可得R2为0.981 9。

单偏心式振动三级枝干加速度响应函数为

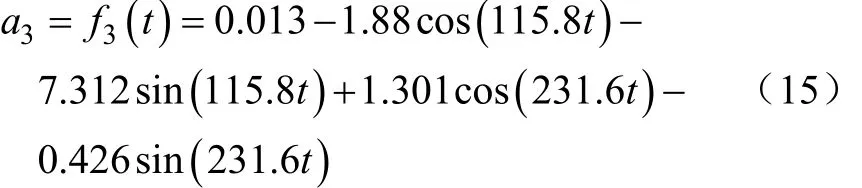
由杏树不同位置振动拟合曲线图 9可知，在杏树受单偏心式振动收获机施加的振动时，各检测点均呈周期性简谐运动，稳态时激振周期为0.05 s（20 Hz）；从振动开始时间看，振动从夹持点树干逐级向树枝传递；由于杏树受扭转振动，且二级枝干处于杏树分叉处，杏树夹持位置振动位移小于三级枝干，相同垂直距离，三级枝干检测处位移约为二级枝干检测处两倍。

4.2.2 对称双偏心式振动收获杏树响应状态

对称双偏心式振动激励下杏树不同位置的振动响应曲线如图10所示。对称双偏心式振动过程中，杏树可视为欧拉-伯努利梁，其函数也符合傅里叶变换形式。对杏树受对称双偏心式振动收获机振动激励达到稳态后的振动数据进行傅里叶拟合分析和求解。振动激励达到稳态后，对1.4～1.5 s内不同位置振动数据进行傅里叶拟合分析，拟合曲线如图11所示。

图10 对称双偏心式振动激励下杏树不同位置响应曲线Fig.10 Response curves of different locations of apricot trees by symmetrical double-eccentric vibration

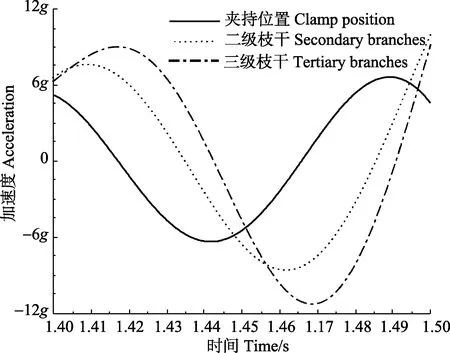
图11 对称双偏心式振动杏树不同位置加速度拟合曲线Fig.11 Fitted curve of acceleration of different locations of apricot trees by symmetrical double-eccentric vibration

由振动响应曲线图10a可知，对称双偏心式振动激励下杏树不同位置响应曲线可知，杏树夹持位置在0.052 s开始振动，0.646 s时达到稳态，夹持位置最大加速度为10.4 g。稳态下0.1 s内夹持位置振动数据傅里叶拟合分析，可得R2为0.906 2。

对称双偏心式振动夹持位置加速度响应函数为

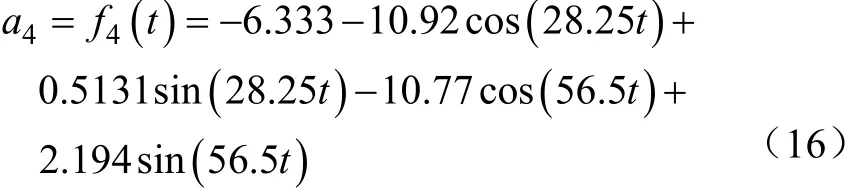
由图10b可知，杏树二级枝干在0.219 s开始振动，在0.764 s时达到稳态，振动过程中最大加速度10.3 g。稳态下0.1 s内二级枝干振动数据傅里叶拟合分析，可得R2为0.939 8。

对称双偏心式振动二级枝干加速度响应函数为

由图10c可知，杏树三级枝干在0.224 s时开始振动，在0.773 s时达到稳态，最大加速度10.4 g。三级枝干0.1 s稳态振动数据傅里叶拟合分析，可得R2为0.93。

对称双偏心式振动三级枝干加速度响应函数为

由杏树振动拟合曲线图11可知，在杏树受对称双偏心式振动收获机施加的振动时，各检测点均呈周期性简谐运动，稳态时激振周期为0.1 s（10 Hz）；从振动开始时间看，振动从夹持点树干逐级向树枝传递；稳态后各级枝干振动最大加速度均能与激振点一致。

4.3 不同激振方式频谱分析

对不同激振方式下测得各位置加速度在0～50 Hz内振动过程进行扫频分析，通过加速度与频率间频谱曲线，研究 2种激振方式下库麦提品种杏树的共振特性和收获所需最佳频率范围。

对杏树—单偏心式收获机振动采收系统工作过程中，杏树各部位加速度变化曲线如图12a所示。在扫频区间内出现了4阶明显的共振频率，在11.56 Hz时，各位置加速度均为测量期间的最大值，其中夹持位置 x与 y方向加速度接近，分别为10.06 g和11.69 g；二级枝干与三级枝干加速度相近，分别为5.31 g和5.95 g。

对杏树—对称双偏心式收获机振动采收系统工作过程中，杏树各部位加速度变化曲线如图 12b所示。在扫频区间内出现了3阶明显的共振频率，在11.56 Hz时，各位置加速度也均为测量期间的最大值，其中夹持位置y方向加速度相对其他测量位置较小；其他各检测点按加速度大小分别为：三级枝干7.95 g、夹持位置7.05 g和二级枝干6.12 g。

杏树最佳收获频率范围在10～20 Hz之间[32]。针对本试验的库麦提杏品种果树，由加速度频谱图12可知，2种方式振动激励下杏树-收获机系统在11.56 Hz的振动频率下各检测点加速度均为最大值。其中，单偏心式振动夹持位置加速度大于各级枝干，即各级枝干在相同频率下振动幅度小；对称双偏心式振动传递到第三级枝干后加速度明显大于夹持位置。相同频率下对称双偏心式振动各级枝干响应加速度大于单偏心式振动，即振动幅度大。

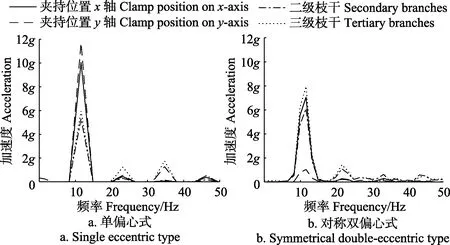
图12 2种振动收获机加速度频谱图Fig.12 Acceleration spectrogram of two kinds of vibration harvester

5 结 论

1）建立杏树振动模型、杏树-采收机动力学模型进行理论分析以及夹持位置处得到的李萨如图形。分析可知：杏树受单偏心式振动激励时，会产生扭转振动，整体运动为轨迹类似于倒圆锥体形，水平截面上运动轨迹为圆形；受对称双偏心式采收机施加的振动激励，沿着夹持位置方向做水平往复振动，整体运动轨迹类似于扇形，水平面上运动为直线。

2）利用安装在杏树不同位置的加速度传感器得到库麦提品种杏树振动响应曲线，测量处由下至上开始振动，时间分别为单偏心式0.135、0.181和0.191 s，对称双偏心式0.052、0.219和0.224 s。由于杏树材料特性和生长的不规律性，单偏心式振动激励下杏树响应比对称双偏心振动响应复杂，在相同枝干位置，振动响应状态不同。

3）通过MATLAB对稳态内0.1 s的振动数据进行傅里叶拟合分析，稳态时单偏心式振动系统周期为0.05 s，对称双偏心式振动系统周期为0.1 s的杏树各测量点振动加速度响应曲线和函数。

4）分析库麦提品种杏树受迫振动频谱图可知，本次试验中库麦提杏树在11.56 Hz频率下，各枝干响应加速度均为最大值；单偏心式振动夹持位置加速度大于各级枝干，对称双偏心式振动传递到三级枝干时加速度高于夹持位置；相同频率下对称双偏心式振动各级枝干响应加速度大于单偏心式振动，更利于振动采收。

[参 考 文 献]

[1] 王丽丽, 郭艳玲, 王迪, 等. 果蔬采摘机器人研究综述[J].林业机械与木工设备, 2009, 37(1): 5－8.Wang Lili，Guo Yanling，Wang Di，et al. Overview of study on fruit and vegetable picking robots[J]. Forestry Machinery& Woodworking Equipment，2009，37(1): 5－8. (in Chinese with English abstract)

[2] 吐鲁洪, 阿依木妮莎, 杜英. 国外果树振动采收机[J]. 新疆农机化, 2004 (3): 54－55.

[3] 散鋆龙, 牛长河, 乔圆圆, 等. 林果机械化收获研究现状、进展与发展方向[J]. 新疆农业科学, 2013, 50(3): 499－508.San Yunlong, Niu Changhe, Qiao Yuanyuan, et al.Development of fruit mechanized harvest and its relevant research[J]. Xinjiang Agricultural Sciences, 2013, 50(3): 499－508. (in Chinese with English abstract)

[4] Tehran K I. Determination of vibrational properties of Shahroudi's almondstem[J]. International Journal of Agriculture and Crop Sciences,2013,5(6):638－645.

[5] Fridley R B, Adrian P A. Some aspects of vibratory fruit harvesting [J]. Agriculture of Engineering, 1960, 41(1): 28－31.

[6] Whitney J D, Churchill D B, Hedden S L, et al. Trunk shakers of citrus harvesting. Part I: Measured trunk shaker and tree trunk motion [J]. Applied Engineering in Agriculture,1988, 4(2)：93－101.

[7] Whitney J D, Smerage G H, Block W A. Dynamic analysis of a trunk shaker-post system [J]. Transactions of the ASAE,1990, 33(4): 1066－1070.

[8] Horvath E, Sitkei G. Damping properties of plum trees shaken at their trunks [J]. Transactions of the ASAE, 2005,48(1): 19－25.

[9] Horvath E, Sitkei G. Energy consumption of selected tree shakers under different operational conditions [J]. Journal of Agricultural Engineering Research, 2001, 80(2): 191－199.

[10] Láng Z. A fruit tree stability model for static and dynamic loading [J]. Biosystems Engineering, 2003, 85(4): 461－466.

[11] Láng Z. Dynamic modelling structure of a fruit tree for inertial shaker system design [J]. Biosystems Engineering,2006, 93(1): 35－44.

[12] Láng Z. A one degree of freedom damped fruit tree model[J].Agricultural Engineering International Cigr Journal, 2008,51(3): 823－829.

[13] Bentaher H, Haddar M, Fakhfakh T, et al. Finite elements modeling of olive tree mechanical harvesting using different shakers[J]. Trees, 2013, 27(6): 1537－1545.

[14] Du X, Chen D, Zhang Q, et al. Dynamic responses of sweet cherry trees under vibratory excitations[J]. Biosystems Engineering, 2012, 111(3): 305－314.

[15] 杜小强, 倪柯楠, 潘珂, 等. 可调振幅单向拽振式林果采收机构参数优化[J]. 农业工程学报, 2014, 30(16):25－32.Du Xiaoqiang, Ni Kenan, Pan Ke, et al. Parameter optimization of stroke-adjustable and monodirectional pulling fruit harvester[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2014,30(16): 25－32. (in Chinese with English abstract)

[16] Wu C, He L, Du X, et al. 3D reconstruction of Chinese hickory tree for dynamics analysis[J]. Biosystems Engineering, 2014, 119(1): 69－79.

[17] 杜小强, 李松涛, 贺磊盈, 等. 三维激振果品采收机构优化设计与试验[J]. 农业工程学报, 2017, 33(16): 48－55.Du Xiaoqiang, Li Songtao, He Leiying, et al. Optimal design and experiment on vibratory fruit harvesting mechanism with three-dimensional excitation[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(16): 48－55. (in Chinese with English abstract)

[18] 蔡菲, 王春耀, 王学农, 等. 基于高速摄像技术的振动落果惯性力研究[J]. 西北农林科技大学学报: 自然科学版,2013, 4: 208－212.Cai Fei, Wang Chunyao, Wang Xuenong, et al. Inertia of fruits abscised by vibration based on high-speed video camera technology[J]. Journal of Northwest A&F University:Nat. Sci. Ed, 2013, 4: 208－212. (in Chinese with English abstract)

[19] 刘子龙, 王春耀, 罗建清, 等. “Y”型果树动力学模型仿真及试验的研究[J]. 农机化研究, 2017, 39(8): 154－158.Liu Zilong, Wang Chunyao, Luo Jianqing, et al. " Y" type of fruit tree dynamic model simulation and experimental research[J]. Research on Agricultural Mechanization, 2017,39(8): 154－158. (in Chinese with English abstract)

[20] 吕梦璐, 王春耀, 罗建清, 等. 基于ANSYS对振动果树枝干“Y”型响应的研究[J]. 农机化研究, 2017, 39(2): 37－41.Lü Menglu, Wang Chunyao, Luo Jianqing, et al. The finite element analysis of the vibration of fruit trees based on ANSYS workbench[J]. Research on Agricultural Mechanization, 2017, 39(2): 37－41. (in Chinese with English abstract)

[21] 魏庭鹏, 王春耀, 闵磊, 等. 基于 MATLAB对"Y型"果树振动共振频率的研究[J]. 江苏农业科学, 2017, 45(3): 169－172.Wei Tingpeng, Wang Chunyao, Min Lei, et al. The resonance frequency of the vibration of fruit trees based on MATLAB[J]. Jiangsu Agricultural Sciences, 2017, 45(3):169－172. (in Chinese with English abstract)

[22] 刘子龙, 王春耀, 许正芳, 等. 海棠果树动力学特性的研究[J]. 农机化研究, 2017, 39(12): 165－169.Liu Zilong, Wang Chunyao, Xu Zhengfang, et al. Study on the dynamic characteristics of begonia fruit trees[J]. Research on Agricultural Mechanization, 2017, 39(12): 165－169. (in Chinese with English abstract)

[23] 张智, 王春耀, 刘子龙, 等. Y型果树的冲击试验[J]. 新疆大学学报:自然科学版, 2017, 34(2): 237－241.Zhang Zhi, Wang Chunyao, Liu Zilong, et al. Y-type fruit tree impact test[J]. Journal of Xinjiang University: Natural Science Edition, 2017, 34(2): 237－241. (in Chinese with English abstract)

[24] 汤智辉, 贾首星, 沈从举, 等. VIBROLIV干果采收机的引进与试验[J]. 新疆农机化, 2009 (4): 38－40.

[25] 汤智辉, 沈从举, 孟祥金, 等. 4YS-24型红枣收获机的研制[J]. 新疆农机化, 2010(1): 30－32.

[26] 汤智辉, 孟祥金, 沈从举, 等. 机械振动式林果采收机的设计与试验研究[J]. 农机化研究, 2010, 32(8): 65－69.Tang Zhihui, Meng Xiangjin, Shen Congju, et al. Design and experimental investigation of mechanical vibration tree fruits and nuts harvester[J]. Research on Agricultural Mechanization, 2010, 32(8): 65－69. (in Chinese with English abstract)

[27] 乔园园, 牛长河, 孟详金, 等. 牵引式林果振动采收机的设计与田间试验[J]. 新疆农业科学, 2015, 52(3): 528－534.Qiao Yuanyuan, Niu Changhe, Meng Xiangjin, et al. Design of traction type fruit harvest machine and its experimental research in fields[J]. Xinjiang Agricultural Sciences, 2015,52(3): 528－534. (in Chinese with English abstract)

[28] 张合军, 王军玮. 几种常用偏心块偏心矩及其激振力的计算分析[J]. 矿山机械, 1999, 27(6): 68－68.

[29] 刘延柱, 陈文良, 陈立群. 振动力学[M]. 北京: 高等教育出版社, 1998.

[30] 中国国家标准化管理委员会. GB/T 1931-2009 木材含水率测定方法[S]. 北京: 中国标准出版社, 2009.

[31] 中国国家标准化管理委员会. GB/T 1938-2009 木材顺纹抗拉强度试验方法[S]. 北京: 中国标准出版社, 2009.

[32] Erdogan D, Guner M, Dursun E, Gezer I. Mechanical harvesting of apricots[J]. Biosystems Engineering, 2003,85(1): 19－28.