永磁式TMD在混凝土箱梁人行桥振动控制中的应用

张斌 王建立 王建 黄燕平 邱玲玲

（隔而固（青岛）结构设计事务所有限公司 266108）

引言

调谐质量阻尼器由质量块、弹簧与阻尼元件组成，最早由Ormondroyd和Den Hartog于1928年提出［1］。其减振机理为：结构在外部激励作用下，带动TMD一起振动，TMD相对于运动产生的惯性力反作用在结构上。通过调谐惯性力，使结构的振动能量最大限度地转移到TMD上，并由其阻尼加以耗散，从而减小结构的振动响应［2］。在大跨度桥梁及高耸结构风致振动控制［3-5］、大跨度及长悬挑结构与人行桥的人致振动控制方面［6-8］，有着广泛的应用。人行桥振动控制典型案例为英国千禧桥，竖向振动控制使用了52套1t～3t重TMD，水平向振动控制使用了8套 2.5t重 TMD［8］。

工程常用的阻尼元件为橡胶及油阻尼器等高阻尼材料，橡胶材料容易老化、阻尼与刚度难以分离，油阻尼器存在漏油风险。而永磁式电涡流阻尼无需与结构接触，不会产生摩擦，内无液体不会漏液，刚度与阻尼参数完全分离，且阻尼参数后期易于调整［9］。电涡流阻尼主要用于航天结构振动控制、汽车减振与刹车及高速列车制动等方面［10］，在人行桥人致振动控制领域研究应用较少。汪志昊等通过建立有限元模型、实验室试验等方式对永磁式电涡流TMD对人行桥人致振动控制进行了详细研究，并进行了TMD设计［11］。

中山市神湾镇某预应力钢筋混凝土箱梁人行桥，为两跨大跨度变截面曲线连续梁桥，理论计算结构一阶垂向固有频率低于3Hz，当大量人员在其上面行走时，可能导致共振影响舒适度。本文对采用永磁式TMD进行人致振动控制，进行了理论计算、永磁式TMD设计与调试及现场实测分析。

1 理论计算分析与TMD设计

人行桥第一跨长34.591m，第二跨长46.412m（简称46m跨），如图1所示。其结构柔度较大，因使用功能需求，人行天桥上部人流较大，为满足响应的舒适度要求，需要对其进行动力分析，确定结构是否需要进行振动控制。

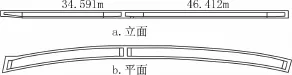
图1 梁桥立面与平面示意Fig.1 Façade and plane of the bridge

1.1 模态分析

根据结构的主要参数及荷载，采用SAP 2000有限元软件建立有限元模型，桥梁采用梁单元模拟，网格尺寸为1m，如图2所示。人行天桥为钢筋混凝土结构，计算中结构阻尼比取为0.015。表1所示为模型计算前3阶固有频率，前两阶阵型为竖向振动，第一阶垂向固有频率为2.12Hz，模态参振质量系数为25.56%；第三阶振型为Y向平动。

图2 有限元模型Fig.2 Finite elementmodel

人行桥一阶垂向固有频率较低，在步行频率范围（1.6Hz～2.4Hz）内。《城市人行天桥与人行地道技术规范》（CJJ 69-95）规定：“为避免共振，减少行人不安全感，天桥上部结构竖向自振频率不应小于3Hz”。根据分析结果，人行桥很可能发生共振，需进行振动控制。

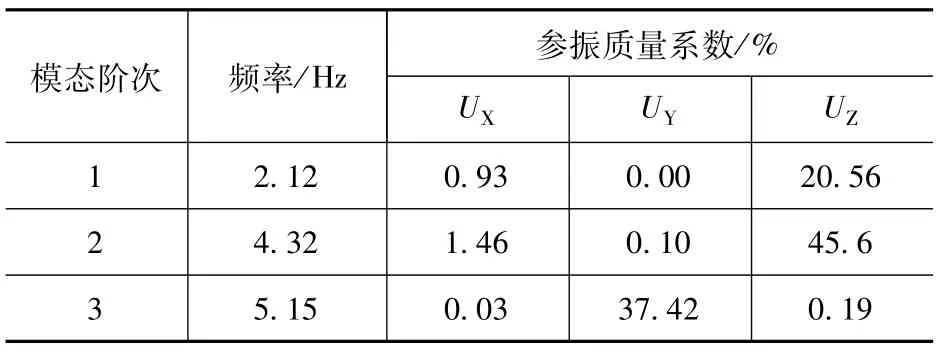
表1 人行桥前3阶频率及各向参振质量系数Tab.1 First three frequencies of footbridge

1.2 TMD减振设计分析

1.振动限值与步行荷载模型

国外在结构振动舒适度方面已经研究多年，美国、日本等国家已经发布了相关的设计指南，国内在该方面研究较少。本文根据美国AISC发布的设计指南中的规定［12］，以0.05g作为控制指标，如表2所示。

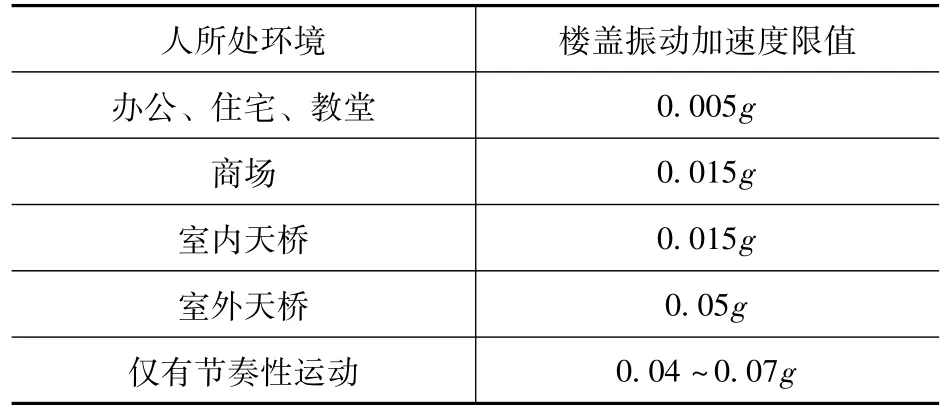
表2 民用建筑楼盖振动加速度限值Tab.2 Acceleration limits of civil structure floor

垂直方向的人行激励时程曲线采用国际桥梁及结构工程协会（IABSE）连续步行的荷载模式，这一荷载模式考虑了步行力幅值随步频增大而增大的特点。假设单人质量m＝75kg，则步行激励力为：

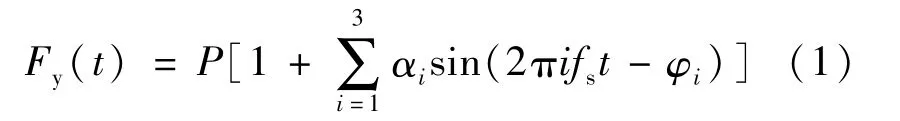
式中：Fy（t）为垂直方向的步行激励力；P＝mn′g，g＝9.8N／kg，n′为同步激励人数；αi为第i阶谐波分量的动力系数，α1＝0.4+0.25（fs-2），α2＝α3＝0.1；fs为步行频率；t为时间；φi为第i阶谐波分量的相位角，φ1＝0，φ2＝φ3＝π／2。

参考国外的研究成果［13］，对步行载荷做进一步假设：

（1）桥面上人员的密度为1.5人／m2（千僖桥开放时的最大人员密度为1.3～1.5人／m2），桥面的面积为81×3.7≈300m2，桥面上共有n＝450人。

（2）人行桥上行人和一阶固有频率同步的人数为：

计算时，步行激励的频率fs为2.1Hz。将由式（1）计算的步行激励以均布荷载的形式加载于全桥桥面上，然后进行时程分析，得到46m跨跨中垂向振动加速度峰值为1.067m／s2（如图4所示），大于舒适度要求，需要采取减振措施。

2.TMD参数及产品设计

文献［14］给出了TMD设计的最优参数：

最优频率比为：

最优阻尼比为：

式中：μ＝md／Ms为TMD质量与主结构模态参振质量比；频率比 β＝ωd／ωs，ωd＝2πfd；md、ωd和fd分别为TMD的质量块质量、固有圆频率和固有循环频率；Ms和ωs分别为主结构的模态参振质量与固有圆频率。

设计TMD质量md为5t，人行桥一阶垂向振动参振质量Ms为156t，计算得出μ＝3.2%。由式（2）计算得出fd≈2.1Hz，由式（3）计算得出最优阻尼比ξdopt＝10.8%。考虑安装运输方便，设置5套TMD，每套质量md1＝1t，分散分布于46m跨跨中位置，如图3所示。

图3 TMD安装位置示意Fig.3 TMD installation position

计算结果如图4所示：安装TMD后，46m跨结构的振动有明显减弱的趋势，跨中垂向振动加速度峰值为0.274m／s2，减振效果可达74.3%。

单个TMD质量、频率与阻尼比经过理论分析确定后，下一步进行产品设计。

永磁式电涡流TMD刚度由螺旋压簧提供，通过改变压簧的数量与型号，可以对TMD频率进行调节。单个TMD总刚度kd1由式（4）计算为：174.1kN／m。受弹簧与安装支座摩擦等因素影响，实际频率会偏大，因此设计频率需要偏低一点。实际刚度取166kN／m。

图4 安装TMD前后46m跨跨中振动加速度响应Fig.4 Vibration acceleration response at themiddle section of46 meterspan with and without TMD

TMD阻尼器主要由永磁体与导体板组成。理论上，同等条件下，导体板的导电性越好，产生的电涡流阻尼就会越大［11］。永磁体选用市场上可购买的N50号钕铁硼（NdFeB）磁铁，剩余磁感应强度为1.4T～1.45T，长度与宽度均为100mm，厚度40mm。导体板选用紫铜片，尺寸为：高度200mm，宽度205mm，厚度10mm。

文献［15］在基于一系列假设的前提下提出电涡流阻尼比ξ的计算公式：

式中：h为导体板厚度，为10mm；B0为永磁体两极表面中心处的磁场强度，取1.4T；L为永磁体在垂直于TMD运动方向的尺寸，为100mm；ρ为导体板的电阻率，其值为1.8×10-8Ω·m；d为导体板与永磁体中心的距离；r0＝L／2。

应用式（5）可以初步确定永磁体使用数量，同时通过调节导体板与永磁体中心距离d使TMD阻尼比达到最优阻尼比。本项目TMD两侧各布置2块永磁体，为形成较短的磁回路，减小磁势损耗，永磁体S与N极交替布置，如图5所示。

图6为固有频率2.1Hz的TMD无导体板与有导体板工况自由振动衰减时程曲线。

未安装导体板时，TMD处于无附加阻尼状态，结构本身阻尼很小，可以忽略不计；安装导体板后，TMD系统阻尼明显提升，振动响应快速衰减。

图5 TMD永磁体与导体板Fig.5 Permanentmagnet and conductor plate of TMD

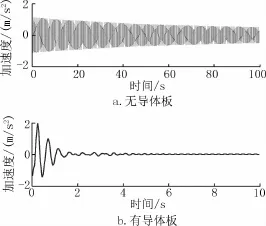
图6 TMD2.1Hz自由振动衰减曲线Fig.6 Free vibration time histories of TMD with 2.1Hz

2 TMD减振效果测试

2.1 TMD现场安装调试

测试仪器为LMSSCADASMobile SCM01采集系统（8通道），Lance MODEL LC0016型高灵敏度加速度传感器，其指标为：灵敏度9.994V／g，量程0.5g，频率范围0.05Hz～300Hz，分辨率2×10-6g，横向灵敏度3.7%，谐振频率1.2kHz，温度范围-30℃～+80℃。

现场调试时，人行桥施工基本完毕，仅剩桥面铺装未完成。桥面铺装层为木材，质量轻，对人行桥固有频率基本没有影响。TMD在现场安装就位以后，如图7所示，处于锁紧状态（TMD不工作），对46m跨进行振动测试分析，采集跨中位置垂向振动加速度响应。将采集的时程数据进行傅里叶快速变换分析，进行10次平均得到频谱数据，如图8所示。人行桥一阶垂向固有频率为2.6Hz，二阶垂向固有频率为4.9Hz。通过改变TMD刚度，将其频率调整至fd＝2.6Hz，与人行桥频率基本一致。根据式（2）最优频率比计算TMD频率应调谐至2.52Hz，受弹簧固定型号影响，频率不易完全吻合。通常情况下，理论计算与实测频率稍有偏差，因此，TMD频率必须在一定范围内可调节，以满足工程实际需求。

图7 人行桥箱梁内TMDFig.7 TMD in box girder

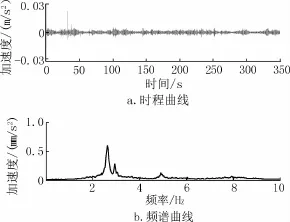
图8 自然激励下人行桥振动时程及频谱Fig.8 Time history and frequency spectrum of footbridge with natural incentive

2.2 减振效果实测分析

在TMD锁紧（TMD未工作）与释放（TMD正常工作）工况下，对桥面进行人行激励，测试TMD减振效果。受现场条件限制，难以采用理论计算的激励模型进行激励，仅采用4人跳跃激励，激励频率为2.6Hz，如图9所示。

图9 四人2.6Hz跳跃激励Fig.9 Jumping incentive of2.6Hz with 4 people

TMD锁紧工况，4人跳跃激励，计算结果取3次测试数据平均值，人行桥振动加速度最大值均值为0.2404m／s2，典型振动时程曲线如图10所示；TMD释放工况，4人跳跃激励，人行桥振动加速度最大值均值为0.1049m／s2，TMD振动加速度最大值均值为0.2301m／s2，典型振动时程曲线如图11所示。

图10 TMD释放前后人行桥振动对比Fig.10 Footbridge vibration of TMD working and notworking

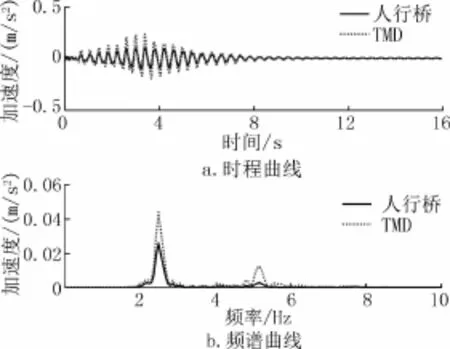
图11 TMD释放后人行桥与TMD振动对比Fig.11 Footbridge vibration contrastwith TMD after TMD working

由图10、图11可以看出：

（1）TMD释放后，人行桥在跳跃激励下，振动减小明显，减振效果为56.4%。激励停止后，振动在3s左右即衰减完毕，而TMD锁紧时，振动衰减时间在10s左右，TMD释放使人行桥的整体阻尼比提升至3%左右。

（2）TMD释放后，TMD振动要大于人行桥的振动，说明人行桥大部分振动传递至TMD，最终由TMD耗散。

（3）由频谱曲线可以看出，TMD对人行桥一阶垂向振动控制效果较好，对二阶垂向振动也有一定控制。

（4）由频谱曲线还可以看出，在主要控制频带附近，存在振动放大频域，分别在2.02Hz、2.19Hz、2.69Hz、2.9Hz附近。

3 结论

通过对某人行桥永磁式TMD理论计算与实测分析，主要得出以下结论：

1.永磁式TMD频率可以根据实测结果进行调节，使其与人行桥固有频率基本一致，以达到良好的减振效果。

2.TMD正常工作后，4人2.6Hz跳跃激励工况下，减振效果达56.4%。TMD耗散了人行桥大部分振动能量，提升人行桥阻尼比至3%左右，使振动衰减时间显著缩短。

［1］樊健生，陈宇，聂建国.人行桥的TMD减振优化设计研究［J］.工程力学，2012，29（9）：133-140 Fan Jiansheng，Chen Yu，Nie Jianguo.Optimum Design of Tuned Mass Damper for Footbridge［J］.Engineering Mechanics，2012，29（9）：133-140

［2］宋璨.磁流变式调谐液体柱阻尼器的建模及对桥梁振动控制的研究［D］.湖南：湖南大学，2009 Song Can.Modeling ofMagneto-rheological Tuned Liquid Column Damper and Research on Bridge Vibration Control with Magnetorheological Tuned Liquid Column Damper［D］.Hunan：Hunan University，2009

［3］Fujino Y，Yoshida Y.Wind-induced vibration and control of Trans-Tokyo Bay Crossing bridge［J］.ASCE Journal of Structural Engineering，2002，128（8）：1012-1025

［4］BarelliM，White J，Billington D P.History and aesthetics of the Bronx-Whitestone bridge［J］.ASCE Journal of Bridge Engineering，2006，11（2）：230-240

［5］李爱群，黄瑞新，赵耕文，等.基于简化模型的北京奥林匹克公园中心演播塔顺风向风振TMD控制研究［J］.振动与冲击，2010，29（10）：170-174 Li Aiqun，Huang Ruixin，Zhao Gengwen，et al.TMD wind-induced vibration control along wind direction for Beijing Olympic center broadcast tower based on its simplified model［J］.Journal of Vibration and Shock，2010，29（10）：170-174

［6］吕西林，丁琨，施卫星，等.上海世博文化中心TMD减轻人致振动分析与实测研究［J］.振动与冲击，2012，31（2）：32-37，150 Lv Xilin，Ding Kun，ShiWeixing，etal.Analysis and field test for human-induced vibration reduction with TMD in Shanghai EXPO culture center［J］.Journal of Vibration and Shock，2012，31（2）：32-37，150

［7］陈政清，刘光栋.人行桥的人致振动理论与动力设计［J］.工程力学，2009，26（Sup.Ⅱ）：148-159 Chen Zhengqing，Liu Guangdong.Pedestrian-induced vibration theory and dynamic design of footbridges［J］.Engineering Mechanics，26（Sup.Ⅱ）：148-159

［8］Tamer M W，Noor A K.Computational strategies for flexible multi-body systems［J］.Journal of Vibration and Shock，2009，28（3）：1-6

［9］汪志昊，华旭刚，陈政清，等.基于微型永电磁式涡流阻尼TMD的人行桥模型减振实验研究［J］.振动与冲击，2014，33（20）：129-132 Wang Zhihao，Hua Xugang，Chen Zhenqing，etal.Experimental study on vibration control of amodel footbridge by a tiny eddycurrent tuned mass damper with permanentmagnets［J］.Journal of Vibration and Shock，2014，33（20）：129-132

［10］Sodano H A，Bae JS.Eddy current damping in structures［J］.The Shock and Vibration Digest，2004，36（6）：469-478

［11］汪志昊，陈政清.永磁式电涡流调谐质量阻尼器的研制与性能试验［J］.振动工程学报，2013，26（3）：374-379 Wang Zhihao，Chen Zhengqing.Development and performance tests of an eddy-current tunedmass damperwith permanentmagnets［J］.Journal of Vibration and Engineering，2013，26（3）：374-379

［12］AISC steel design guide series11.Floor vibrations due to human activity［S］.Chicago：America Institute of Steel Construction，2003

［13］RFS2-CT-2007-00033，Hivoss（human induced Vibration of Steel Structure）：design of footbridges guidline EN03（2007）［R］，Germany：Research Found for Goal＆Steel，2008

［14］李爱群.工程结构减振控制［M］.北京：机械工业出版社，2007

［15］王翔，王波，汪正星，等.永磁式调谐质量阻尼器参数研究［J］.世界桥梁，2013，41（2）：53-57 Wang Xiang，Wang Bo，Wang Zhengxing，et al.Study of parameters of permanent magnet tuned mass damper［J］.World Bridges，2013，41（2）：53-57