海上风力发电用SeaStar张力腿平台的结构优化分析

毕继红 周月 关健

（1.天津大学建筑工程学院 300072；2.滨海土木工程结构与安全教育部重点实验室（天津大学） 300072）

引言

在深水区（水深＞60m），固定式风力机无法满足经济性要求，海上漂浮式风机是最合适的选择［1］。张力腿平台作为三大漂浮式基础之一，在理论和实验方面的研究还不够完备。

众多国内外学者从张力腿平台的动力响应、强度分析和结构优化三个方面进行研究。Wang等［2］分析了张力腿平台六个自由度方向的运动响应以及塔座的受力情况，提出了减小结构艏摇运动的建议。Kumar D等［3］利用随机平均技术和简化的Fokker-Plank方程，研究了TLP系绳在横向振动中的随机稳定性。余建星等［4］基于累积损伤理论得到平台关键节点的疲劳可靠性。姜哲等［5］通过有限元分析对比了浮箱内的横向框架有支柱和无支柱两种结构形式引起的不同结构应力。Yan等［6］提出一种适应中等水深的潜水式张力腿平台，在运输和安装过程中始终保持良好的稳定性。Jeong Du Kim等［7］将平台和拉索作为多目标优化系统，开发了以平台总重量最小和垂荡位移最小为目标的函数。

SeaStar张力腿平台已有20多年的研究历史。1994年，Kibbee等［8］首先提出 SeaStar张力腿平台的概念，它由一根中心圆柱、三个完全浸入水中的浮筒、三根连接在浮筒上的张力腿组成。Lake等［9］对 SeaStar张力腿平台拉索布置方式进行优化，改善了平台的横摇和纵摇性能。李英［10］对SeaStar浮式风机基础进行基于水动力与空气动力耦合的动力响应分析。闫发锁等［11］基于三维势流理论频域方法对SeaStar等张力腿平台进行水动力参数的分析比较。程阳［12］通过基于雨计数的S-N曲线，对SeaStar等张力腿平台的筋腱的疲劳寿命进行研究。朱婧迪［13］采用第二代非支配排序遗传算法对SeaStar张力腿平台浮筒壳体进行结构优化设计。

现阶段大部分的张力腿平台采用钢结构形式，对材料性能和焊接工艺要求高，耗资巨大。而钢筋混凝土SeaStar张力腿平台具有成本低、受力性能和运动性能良好的优点。因此本文在总结前人的理论和经验的基础上，通过对SeaStar张力腿平台在海洋中多种荷载联合作用下的静力分析和结构优化，得到其受力性能和运动性能的相关结论，为今后该平台的研究提供借鉴。

1 SeaStar张力腿平台有限元模型

SeaStar张力腿平台位于日本秋田市某海域，该区域为深水水域，全年风速高，海域面积辽阔，为海上风机的运行提供了良好的工作条件。该发电风力机由叶片、塔架、浮式支撑基础、锚泊系统和底部基础五个部分构成。风力机额定功率5MW，浸水深度为100m。进行静力分析的目的是为了保证在使用寿命内，结构能够承受工作荷载和环境荷载的作用［14］。

1.1 几何尺寸

如图1所示，张力腿平台本体由长立柱、短立柱、浮筒组成，每个浮筒的两侧通过连接件连接拉索。

该平台本体的各个构件的截面厚度均为0.4m，长立柱外径8m，高33m，浸水深度23m。短立柱外径14m，高13m，浸水深度13m。浮筒为外径10m～12m的变截面构件，距离立柱轴线26.5m。长立柱顶连接薄壁钢塔架。浮筒内支撑竖直，沿浮筒长2.5m。拉索直径157mm，长85m。

图1 SeaStar张力腿平台的几何模型Fig.1 The geometric model of SeaStar TLP

1.2 单元选取及网格划分

在ABAQUS中，立柱和浮筒均为薄壁构件，其厚度远小于其典型整体结构尺寸的1／15，故忽略横向剪切变形，采用计算薄壳结构的通用壳单元S4R进行模拟分析。如图2所示，壳单元的应力应变沿着厚度方向是变化的，一般采用五个积分点便可以满足计算要求。平台本体构件两两相交处应力集中，对该区域加密网格。连接件为混凝土实体材料，采用实体单元C3D8R进行模拟。拉索采用桁架单元T2D2，为了符合拉索的柔性特征，将每根拉索分割为70个单元，有限元模型见图3。

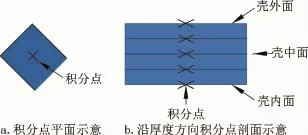
图2 S4R的积分点Fig.2 Integration point of S4R

平台主体和连接件均为混凝土材料，采用绑定约束。在整个分析过程中，两者保持紧密相连。拉索和连接件间采用共用节点的方式连接。

整个结构共有12240个单元，13070个节点。

图3 张力腿平台的有限元模型Fig.3 Finite elementmodel of TLP

1.3 本构模型

张力腿平台主体采用混凝土材料，弹性模量E＝19.5GPa，泊松比ν＝0.2，为模拟真实重力，密度采用钢筋混凝土的密度ρ＝2600kg／m3。拉索采用钢缆，弹性模量为E＝196GPa，泊松比ν＝0.3。在海水中的拉索通过自身的张力来维持整体结构的稳定，将拉索设为只能受拉、受压则失效的特性。

1.4 边界条件以及荷载

张力腿平台的拉索底部通过吸力锚基础连接到海底，因此在拉索底部设置铰接的边界条件。

本文中的SeaStar平台受到重力、浮力、风荷载和波浪力等多种荷载作用，其动力效应随当地环境变化非常复杂。因此，本文采用静力拟动力的计算方法，对混凝土张力腿平台进行初步设计，考虑以下荷载组合：

（1）恒荷载：风机传递的压力、平台重力和静水压力。风机传递的压载共6370kN以壳的边荷载的形式施加到长立柱的上沿。平台本体上施加随深度增加而线性增大的静水压。

（2）活荷载：每根拉索作用在平台上的锚泊力。

（3）环境荷载：根据DNV挪威船级社规范及日本东京大学自主开发的流体软件，计算可得风机正常工作时波高2m，波浪力以5.4kN／mm2的压力施加到浮筒的下表面，以2.0kN／mm2的压力施加到短柱底；本文的风向角为0°，风向规定如图4所示。常风状态的平均风速为12.5m／s，风荷载作用在风机的叶片和塔架上。依据力的平移定理，将风荷载转化为均布在短立柱上表面的水平力和弯矩，水平力大小为600kN，纵摇弯矩为54000kN·m。

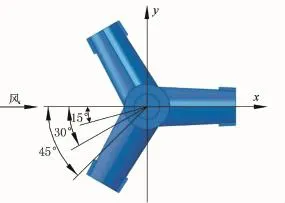
图4 风向角示意Fig.4 Schematic diagram of the wind

张力腿平台的平面内刚度小，在风荷载的作用下产生较大的水平位移。因此计算过程中开启几何非线性。

2 结果分析

实际工程中，平台本体和连接件采用钢筋混凝土材料。由于平台本体和连接件处于海水中，不允许材料进入塑性状态，本文中将平台本体和连接件设为混凝土材料，进行弹性分析，求得应力后再进行配筋设计。

2.1 位移分析

如图5所示，张力腿平台的最大位移出现在长立柱的柱顶，大小为1.37m。结构的纵荡位移大，垂荡位移小，总位移近似等于纵荡位移。由风荷载引起平台纵摇，浮筒1的高度较浮筒2和浮筒3的高度低。

2.2 应力分析

如表1所示，在0°风载作用下，结构纵摇引起拉索1和拉索2、拉索3和拉索6、拉索4和拉索5的应力相同。与浮筒1相连拉索的索力合力最小，浮筒2和浮筒3对应的索力合力最大。

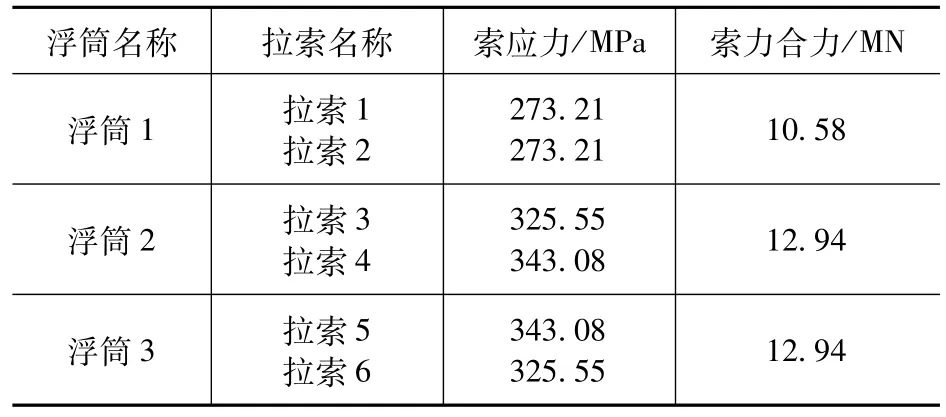
表1 索力值Tab.1 Cable force value

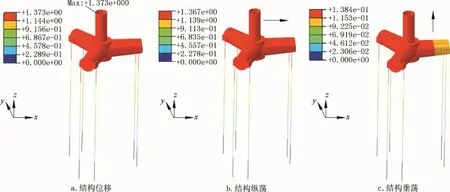
图5 位移（单位：m）Fig.5 Displacement（unit：m）

壳单元的厚度为0.4m，接触空气或者水的外表面、内部封闭部分的内表面以及中面的应力各异，因此分层分析壳的受力状态。

平台本体的内、外层第一、三主应力分别如图6所示。可以发现，绝大多数区域的拉、压应力都很小，有少部分区域应力集中现象严重。

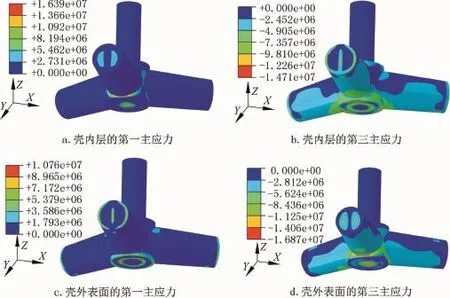
图6 壳的内外层的主应力（单位：Pa）Fig.6 Principal stress of the inner and outer layers of the shell（unit：Pa）

短立柱和浮筒2、浮筒3下表面的相交处的内层受拉，外层受压，该区域的拉、压应力大小 分 别 为 16.39MPa、-16.87MPa，均为最值，为整个平台本体中最危险的区域。这是由浮筒2和浮筒3所受索力合力较大且浮筒长作为力臂长引起较大弯矩造成的。同时，在拉索引起的弯矩作用下，短立柱和浮筒2、浮筒3上表面的相交处内层受压，外层受拉。短立柱和浮筒上、下表面相交处的应力规律相反。

短立柱的柱底同样出现应力集中现象。在长、短立柱的侧面和短立柱的底面交界处都出现了壳外层受拉、内层受压的受力特点。内层最小主应力出现在短立柱柱底边缘，大小为-14.71MPa，外层最大主应力出现在短立柱柱底和长立柱相交处，大小为10.76MPa。

3 结构优化及静力分析

3.1 优化结构的有限元模型

由初始结构的静力分析结果可知，绝大部分区域应力较小，可以适当减小截面尺寸，对于少部分区域出现的应力集中现象，可以通过改变截面的厚度或增加内支撑的方式来改善。

保证其平台本体外侧尺寸不变，则排开水的体积不变，通过改变构件内径的大小来改变截面的厚度。

如表2所示，优化前浮筒和立柱侧面的截面厚度均为0.4m，优化后浮筒的截面厚度均匀变化，浮筒端部截面厚度为0.3m，靠近立柱一端浮筒的截面厚度为0.45m。短立柱侧面的厚度也增加至0.45m。

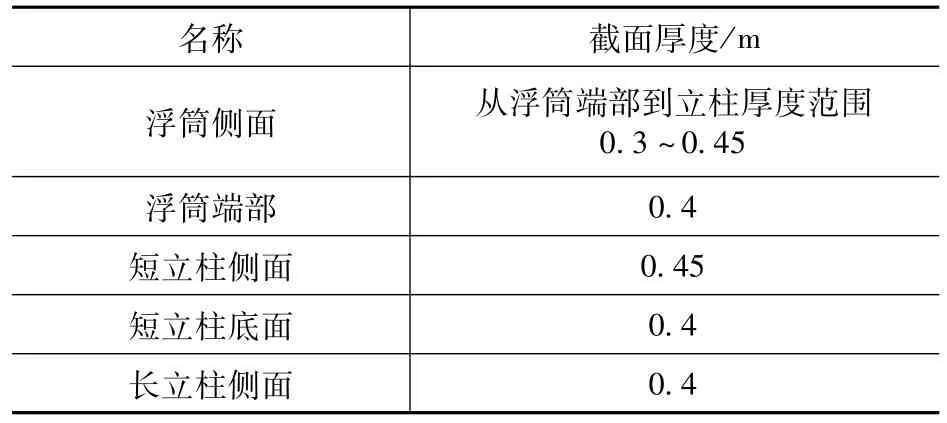
表2 浮筒截面厚度变化Tab.2 Changes in the thickness of the platform body

如图7所示，在长立柱的最底部设置混凝土内支撑板，混凝土板高2m，厚0.3m，共三个，两两夹角120°。

图7 短立柱柱底和长立柱内支撑Fig.7 Short column bottom and long column support

同初始结构相比，优化后结构的网格划分方式、单元类型、本构模型、边界条件、荷载种类不变。结构优化后平台本体尺寸的变化导致重力发生了变化，其他的荷载大小不变。

通过表3可知，优化后平台本体的总体积减小，则重力减小，拉索索力增大，因而拉索抗侧移刚度增大，结构的最大位移减小。索力增大同样会引起平台本体应力增大，而增加截面厚度和设置支撑会引起平台应力减小，因此为讨论结构优化对平台应力的影响，对优化后的张力腿平台进行静力分析。

3.2 优化结构的位移分析对比

将平台优化前后位移对比整理如表4所示。优化后结构拉索的应力增大，最大垂荡位移增大。结构的抗侧移刚度增大，引起平面内运动的位移减小，总位移减小，有利于平台的安全。

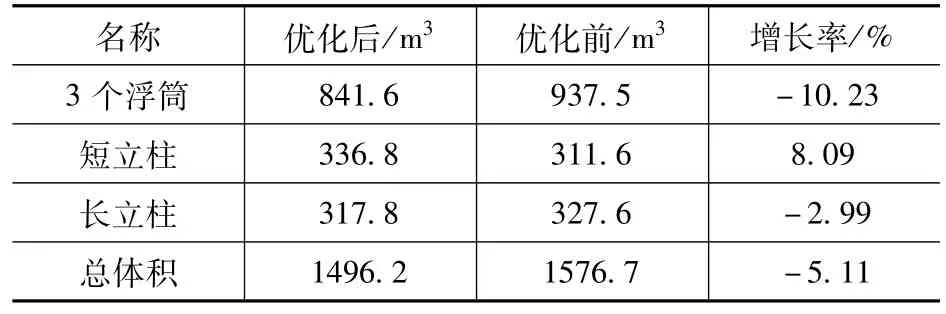
表3 平台本体体积的变化Tab.3 The volume change of platform body

表4 平台位移对比Tab.4 Platform displacement comparison

3.3 优化结构的应力分析对比

由表5可知，每根拉索的应力增大约为24MPa，可见，重力下降引起的索力增大值几乎均匀地分布在每根拉索上。拉索应力增加量较小，因此并不会对拉索是否达到抗拉强度产生决定性的影响。

为了对比结构优化前后应力的变化，将最危险的部位整理如表6所示。

表5 拉索应力对比Tab.5 Comparison of cable stress

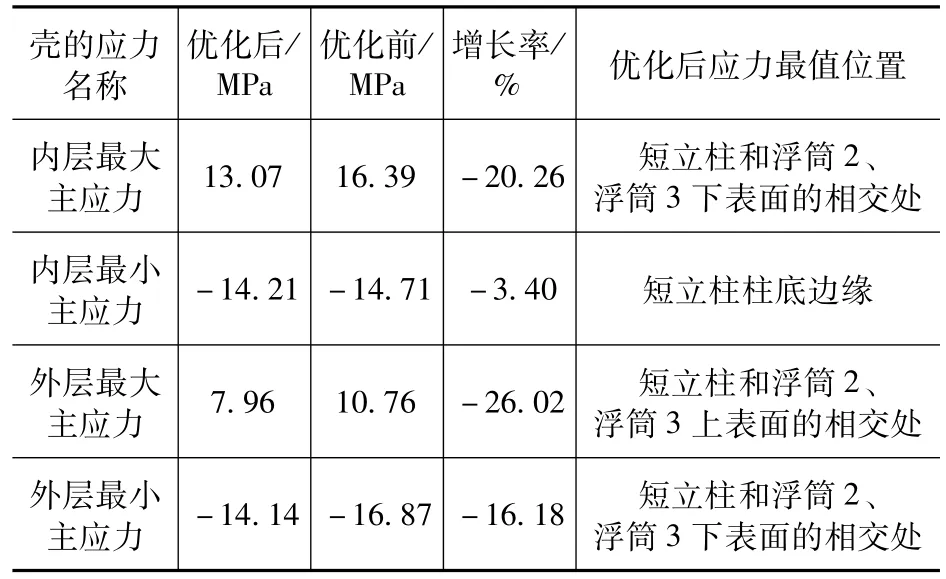
表6 壳体内外层最危险区域Tab.6 Themost dangerous area of the shell inner and outer layers

由表6可知，优化前后外层最大主应力的最值位置发生了变化，其余应力最值位置不变。

优化前外层的最大主应力为短立柱柱底和长立柱相交处，在该处设内支撑之后，增加了局部刚度和变形协调能力，减小了局部的变形。该处的最大主应力大小变为3.75MPa，变为以前应力的34.85%。

由于截面厚度的增加，优化后外层最大主应力的位置为短立柱和浮筒2、浮筒3上表面的相交处，最大主应力减小26.02%。优化后短立柱和浮筒2、浮筒3下表面交界处内层最大主应力减小20.26%，外层最小主应力减小了16.18%，这些区域都更加安全。短立柱柱底厚度不变，最小主应力变化并不明显。

经过优化后的结构对材料的利用更加经济合理，最小主应力小于混凝土的抗压强度，需要重点考虑平台本体的最大主应力，优化后的平台本体的最大主应力明显减小，有利于平台本体的安全。可见，对初始结构进行结构优化对需要重点考虑的上部平台本体是十分有利的。

4 结论

本文基于ABAQUS建立海上风力发电用Sea-Star张力腿平台的数值模型，根据得到的平台本体的应力分布规律进行结构优化，分析对比了优化前后结构的应力和位移，得到的结果如下：

1.结构优化前，短立柱和浮筒2、浮筒3下表面相交处为最危险的区域。该区域内层拉应力、外层压应力分别为16.39MPa、-16.87MPa。

2.结构优化后，平台主体的内、外层最大主应力分别减小了20.26%和26.02%。短立柱柱底和长立柱相交处的最大拉应力减小了65.15%。

3.结构优化后，每根拉索的应力增大约24MPa，结构的平面内位移减小了8.49%，最大位移减小了8.30%。

可见，通过改变平台本体截面厚度和设置内支撑等方式，增加了材料的利用率，减小了危险区域的应力，本文方案为SeaStar张力腿平台的结构选型提供了借鉴。

［1］张亮，吴海涛，荆丰梅，等.海上漂浮式风力机研究进展及发展趋势［J］.海洋技术学报，2010，29（4）：122-126 Zhang Liang，Wu Haitao，Jing Fengmei，etal，Study on offshore floating wind turbine and its development［J］.Ocean Technology，2010，29（4）：122-126

［2］Wang H F，Fan Y H.Preliminary design of offshore wind turbine tension leg platform in the south china sea［J］.Journal of Engineering Science＆Technology Review，2013，6（3）：88-92

［3］Kumar D，Datta T K.Stability of TLP tether using a stochastic averaging technique［J］.Ocean Engineering，2016，118：130-137

［4］余建星，刘杰，余杨，等.基于累积损伤的张力腿平台疲劳及时变可靠性评估［J］.天津大学学报，2016，49（9）：896-901 Yu Jianxing，Liu Jie，Yu Yang，et al.Fatigue Reliability and Time-Dependent Reliability Assessment on TLP Based on Cumulative Damage Theory［J］.Journal of Tianjin University，2016，49（9）：896-901

［5］姜哲，崔维成，李阳，等.张立腿平台浮箱框架结构强度分析方法研究［J］.舰船科学技术，2016，38（19）：56-61 Jiang Zhe，CuiWeicheng，Li Yang，etal.Research on the structural strength analysismethod of tlp pontoon bulkheads［J］.Ship Science and Technology，2016，38（19）：56-61

［6］Han Y，Le C，Ding H，et al.Stability and dynamic response analysis of a submerged tension leg platform for offshore wind turbines［J］.Ocean Engineering，2017，129：68-82

［7］Kim JD，Jang B S.Application ofmulti-objective optimization for TLP considering hull-form and tendon system［J］.Ocean Engineering，2016，116：142-156

［8］Kibbee S，Chianis J，Davies K B，etal.The Seastar Tension-Leg Platform［J］.Tension Leg Platforms，1994

［9］Lake M，He H，Troesch A W，et al.Hydrodynamic Coefficient Estimation for TLP and Spar Structures［J］.Journal of Offshore Mechanics＆Arctic Engineering，1999，122（2）：118-124

［10］李英，钱丽佳，程阳.TLP风机基础二阶动力响应研究［J］.海洋工程，2017，35（3）：52-58 Li Ying，Qian Lijia，Cheng Yang.Investigation of the secondorder hydrodynamic response of TLP wind turbine system［J］.The Ocean Engineering，2017，35（3）：52-58

［11］闫发锁，刘浩，苏威，等.不同结构形式张力腿平台水动力参数比较分析［J］.海岸工程，2017，36（2）：1-8 Yan Fasuo，Liu Hao，Su Wei，et al.A Comparative Study on the Hydrodynamic Parameters of Different Tension Leg Platforms（TLP）［J］.Coastal Engineering，2017，36（2）：1-8

［12］程阳.南海TLP风机基础水动力响应研究［D］.天津大学，2016 Cheng Yang.Investigation of Foundation Hydrodynamic Response of TLPWind Turbine in the South China Sea［D］.Tianjin University，2016

［13］朱婧迪.基于NSGA-Ⅱ的海星浮筒壳体结构优化［D］.大连理工大学，2016 Zhu Jingdi.Structure Optimization of the Seastar Pontoon Shell Based on NSGA-Ⅱ［D］.Dalian University of Technology，2016

［14］李润培，王志农.海洋平台强度分析［M］.上海交通大学出版社，1992 Li Runpei，Wang Zhinong.Strength Analysis of Offshore Platform［M］.Shanghai Jiaotong University Press，1992