斜交箱梁桥最不利地震波输入方向研究

顾红飞

（中设设计集团股份有限公司 南京210014）

引言

对桥梁的抗震设计来讲，地震波输入方向至关重要。关于桥梁的地震波输入方向，我国《公路桥梁抗震设计细则》［1］（2008版）第5.1.1条中规定，一般情况下可只考虑水平向地震作用，即分别按顺桥向和横桥向单独输入地震波后再分别计算桥梁在两个方向的地震力。对直桥而言，采用该种方法计算所得结果能较好地指导设计。但对于斜桥来讲，由于采用不同的地震波输入方向，其计算结果对结构的内力影响较大，若仍按常规方法计算，并不能得到最不利响应量，对设计而言是偏于不安全的。因此寻找一种简单又有效的方法来确定某一响应量的最不利地震波输入方向是很有意义的。

1 最不利地震波输入方向的理论解

A.M.Athanatopoulou在各方向相应量能够线性叠加的前提下，推导了采用时程计算时结构的最不利地震波输入方向的理论公式［3］，推导过程较繁琐，笔者也在文献［1］中对其做了详细推导，其基本思路如下：假设地震波输入方向的坐标系用Opwz表示，整体坐标系用Oxyz表示，两者z坐标轴相同。地震波输入方向与整体坐标系的夹角用θ（p轴绕x轴逆时针旋转）表示，如图1所示。

图1 坐标系与地震波输入方向Fig.1 Coordinate system and seismic input direction

地震波沿p、w和w、-p方向输入后，计算得到某一个响应量R的最大值包络图，从包络图中找到最大值发生的时刻tcr。然后分别沿p、w和w、-p两个方向单独输入双向地震波，得到tcr时刻对应的响应量R，p（tcr）、R，w（tcr），那么对于响应量R的最不利地震动输入方向θcr可按下式计算［3］：

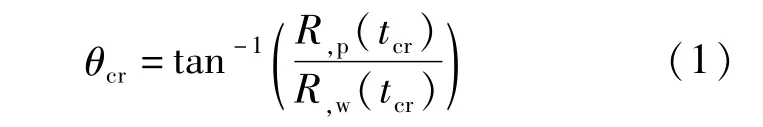
式中：tcr为响应量R达到最大值时对应的时刻；θcr为地震波最不利输入方向与整体坐标系X的夹角；R，w（tcr）为在时刻tcr时，地震波沿w、-p方向输入时响应量R的最大值；R，p（tcr）为在时刻tcr时，地震波沿p、w方向输入时响应量R的最大值。

2 斜交箱梁桥计算分析

从震害统计结果来看，桥墩主要有受弯破坏和剪切破坏两种典型震害。因此，本文主要以桥墩墩底内力为分析对象。选取1#墩墩底截面为计算截面，桥墩编号如图2所示。

图2 桥墩编号Fig.2 Pier number

2.1 建立模型

选取两跨20m的斜交箱梁桥（斜度φ为0°到60°）为计算模型，其中桥墩为圆柱形，直径1.2m，墩高6.4m。墩底按固结处理，支座则采用板式橡胶支座。桥墩单元坐标系中的z、y、x轴分别表示顺桥向、横桥向和轴向。地震波则采用较为典型的两条水平向的El Centro地震波，其时程曲线见图3。

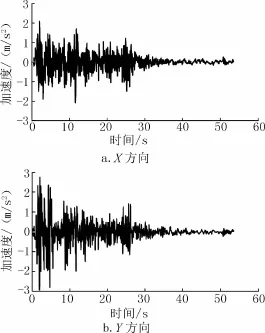
图3 水平地震动Fig.3 The horizontal vibration

2.2 计算结果分析

以斜度45°、墩底弯矩My为例，沿与整体坐标系XOY成0°和90°夹角输入地震波，计算得到M，0和M，90的时程数据，绘制、的包络曲线，其结果如图4所示（斜度45°），从图中可以看出，墩底My最大弯矩值Mmax＝2998kN·m，最小弯矩值Mmin＝-2998kN·m，对应时刻tcr为2.36s。同时在tcr＝2.36s时，双向地震波分别沿0°和90°单独输入时，墩底最大弯矩为M，0＝-2287kN，M，90＝-1938kN，计算可得θcr＝40.3°。同样，当地震波沿θcr＝-139.7°输入地震波时，理论上可以得到My的最小值。沿40.3°和-139.7°输入双向地震波，计算得到My的包络图。为便于比较，将理论计算结果和有限元模型计算结果放入同一图中，如图5所示。

图5中+M对应图4中Mmax，-M对应图4中Mmin，均为理论计算结果。从图5中可以看出，当地震波沿θcr方向输入时的理论计算结果与有限元计算结果基本一致。

图4 横桥向弯矩My（斜度45°）Fig.4 Transversal bendingmoment My（Slope 45°）

图5 横桥向弯矩MyFig.5 Transversal bendingmoment My

其他斜度对应的墩底内力最大值和地震波输入方向的计算结果列于表1中。

表1中各参数含义如下：Vx、Vy、Vz为桥墩轴力、横桥向和顺桥向剪力值；Mx、My、Mz为桥墩扭矩、横桥向和顺桥向弯矩值；Rθ为地震波沿最不利方向输入时墩底各内力的响应值。θcr为地震波沿最不利输入方向与整体坐标系X的夹角；Rθ＝0表示地震波沿X方向输入时墩底各内力的响应值；δR为地震波沿最不利方向输入与沿X方向输入时，墩底各内力的差值百分比。

从表1中数据可以看出：

（1）斜度不同时，墩底弯矩和剪力的最大值及对应的最不利地震波的输入角度各不相同，但最大值出现的时间基本相同（2.7s），该时刻为对应地震波峰值加速度达到最大时。

（2）基于本文所建模型，按常规方向输入地震波计算所得墩底内力的最大值与按理论公式计算所得墩底内力的最大值相差较大。

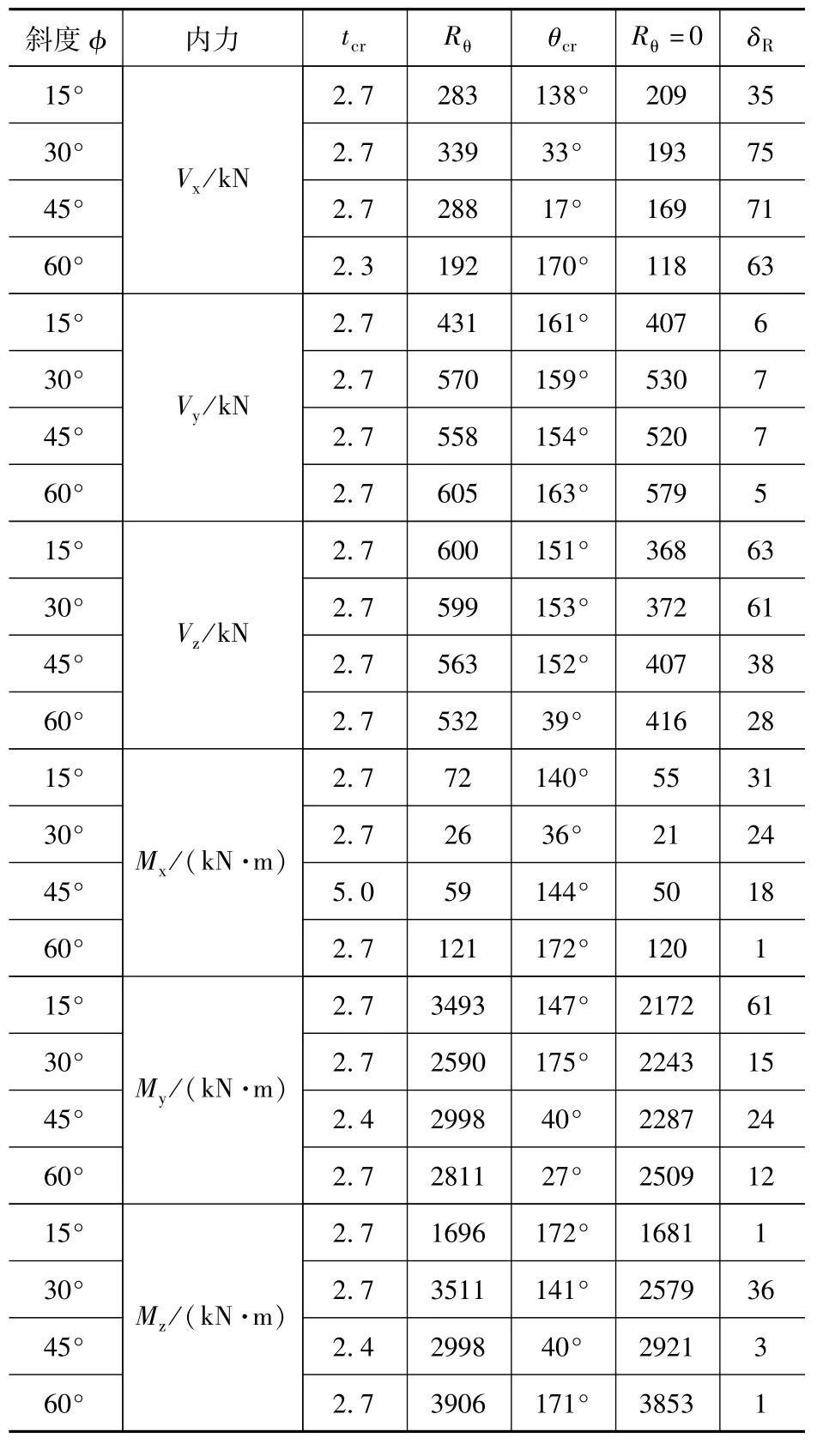
表1 各斜度对应的计算结果汇总Tab.1 The Summary of the calculation result of each slope

3 地震波输入方向的评价曲线

在实际工程中，桥梁种类繁多，假如每座桥的每个内力值都要去寻找最不利地震波输入方向，工作量将非常巨大。因此，本文以斜度为主要变化参数，对斜交箱梁桥墩底内力进行系统的计算分析，以期能为同类桥梁的设计提供部分有价值的参考［2］。

以沿横桥向和纵桥向同时输入时计算所得的结构某一响应量的最大值作为分母，按最不利地震波输入方向时计算所得的结构某一响应量的最大值作为分子，定义一个影响系数r（θi），公式如下：

式中：θi从0°到180°变化。图6a～e分别给出了两跨20m的斜交箱梁桥（斜度分别为0°、15°、30°、45°、60°）桥墩墩底内力的r曲线图，θ为地震波输入方向。

图6 斜度为0°～60°时的r曲线Fig.6 rcurve when the slope is 0°～60°

从图6a中可以看出，斜度为0°时，Vz和My的r曲线基本一致；当θ在0°到140°时呈抛物线形状，大约在80°左右时到达最大值，当 θ在140°到180°时r值基本接近1；Vx和Vy的r曲线完全一致，且最大值在1左右，最小值在0.5左右；而Mx的r曲线基本在1附近。

从以上计算结果可以看出，斜度为0°时，Mx对地震波输入方向不敏感，按常规方法输入时，Vz和My的计算结果偏于不安全，Vx和Vy的计算结果偏于安全。

对比图6a～e可以看出，斜度不同时，不同墩底内力的r曲线也不一致。

r曲线虽然可以用来评估某个响应量按常规方法进行抗震设计时的安全性，但其仅能反映一个响应量对地震波输入方向的敏感程度。如果存在多个响应量的话，那么对于每一个响应量，均需要求出其有可能的最大值，而每个响应量取得最大值时，地震波输入的方向也是不一样的，这样在评估结构的安全性上变得毫无规律。

以按最不利方向θcr输入地震波时的结构某一响应量的最大值作为分母，按任意方向θ输入地震波时的结构某一响应量的最大值作为分子，引入另一个参数 β（θi），定义如下［2］：β（θi）＝。当地震波是唯一时，对结构响应量而言，是固定不变的，可以通过θ＝0°和 θ＝90°计算得到。由此可以得到，其中aj（t）＝tan-1，下标j表示不同的响应量。对于仅一个控制参数，其β曲线可以表示为余弦函数，对于多个控制参数，只是移动的角度不一样。因此，当有两个控制参数时，可以采用绝对值相加的方法进行组合，即：

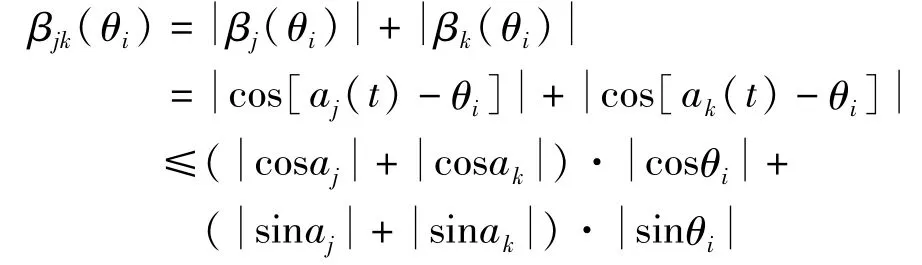
θi不影响以上公式右边的最大值，只影响到取得最大值对应的角度，故［2］：

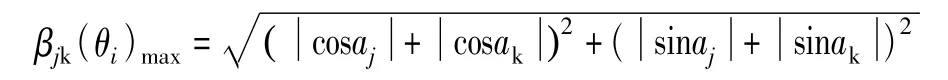
通过计算可以得到以Vy和Vz作为响应量的β曲线（见图7）。当斜度从0°到45°变化时，曲线走势和最大值都比较接近，最大为1.6，对应的地震波输入方向为30°；当斜度为60°时，β最大值为1.8，对应的地震波输入方向为10°。

图7 以Vy和Vz作为控制参数的β曲线［2］Fig.7 βcurve with Vy and Vz as control parameters［2］

5 结论

本文介绍了利用时程分析法求解最不利地震波输入方向的理论计算公式，并以斜交箱梁桥墩底内力为响应量，将理论计算结果与有限元模型计算结果进行对比。同时针对不同斜度的斜交箱梁桥，按常规方法输入地震波时，给出了评价墩底内力是否安全的r曲线和β曲线，得到如下结论：

1.利用时程分析法按理论公式计算所得的最不利输入方向与按有限元模型计算的结果较为吻合。

2.按常规方向输入地震波所得响应量的最大值与按最不利地震波方向输入计算值相差较大，且对不同的响应量，其影响程度各异；若地震波按常规方向输入，对于某些响应量的计算结果是偏于不安全的，在设计计算时应引起重视。

3.r曲线能较好地反映某一响应量对地震波输入方向的敏感程度，较容易判断墩底内力按常规方向输入时计算结果是否偏于安全。

4.β曲线能较好地反映多个响应量对地震波输入方向的敏感程度。对不同斜度的斜交箱梁桥，β曲线走势和最大值都比较接近。

［1］JTJ／T B02-01-2008公路桥梁抗震设计细则［S］JTG／TB02-01-2008 Guidelines for Seismic Design of Highway Bridges［S］

［2］顾红飞.斜交箱梁桥地震响应特性分析［D］.成都：西南交通大学，2011 Gu Hongfei.Analysis on seismic response characteristics of skewed box-girder bridge［D］.Chengdu：Southwest Jiaotong University，2011

［3］A.M.Athanatopoulou.Critical orientation of three correlated seismic components［J］.Engineering Structures，2005（27），301-312

［4］桌秋林.公路简支梁桥地震响应分析［D］.福州：福州大学，2004 Zhuo Qiulin.Seismic Response Analysis of Highway Simple Beam Bridge［D］.Fuzhou：Fuzhou University，2004

［5］范立础，聂利英，李建中.复杂结构地震波输入最不利方向标准问题［J］.同济大学学报，2003，31（6）：631-636 Fan Lichu，NIE Jianying，LI Jianzhong Discussion on Standard of Critical Angle of Seismic Wave in Seismic Analysis of Complicated Structures［J］.Journal of Tongji University，2003，31（6）：631-636