弹性地基上矩形板弯矩计算表编制探讨

周晨

（南京市市政设计研究院有限责任公司 210008）

引言

水池的底板一般是放置于地基上的，大型水池底板厚度相对于其平面尺寸较小，在计算内力时有必要考虑底板与土的共同作用，工程计算时常采用Winkler模型考虑地基与底板的共同作用。

在矩形水池分块简化计算时，采用普通的弹性板计算表［1］是不能考虑底板与地基共同作用的。本文试图编制Winkler地基上矩形板内力计算表，以便在水池简化计算时考虑Winkler地基模型。

1 表格适用条件设定

与弹性地基上板的弯矩相关的因素较多，包括支座条件、地基参数、板的平面尺寸、板厚、板的荷载、板的弹性模量、板的泊松比等。对于Winkler地基模型，地基参数是基床系数。弹性地基上的有限长的板的内力是外荷载和地基反力共同作用的结果。支座约束不是必须的，但不同的边界条件有不同的内力。

一定边界条件下的、有限边长的、Winkler地基上的矩形板弹性力学解是比较复杂的，采取有限元法计算是比较简便的一种方法。

本文设定的边界条件为：板周边有着均匀竖向变形，而转动方向包括了是否允许自由转动两种情况，板面总反力等于边缘力的总和，如图1所示。以上假定条件在通用的有限元软件中没有对应的功能，本文提出了采用基于有限元迭代法的计算方法，避免了文献［2］中采用的在板周边人为添加大刚度竖向弹簧边界单元的方法。本文采用的计算方法符合实际需求，同时还可以拓展用于其他多种地基模型上板的计算。

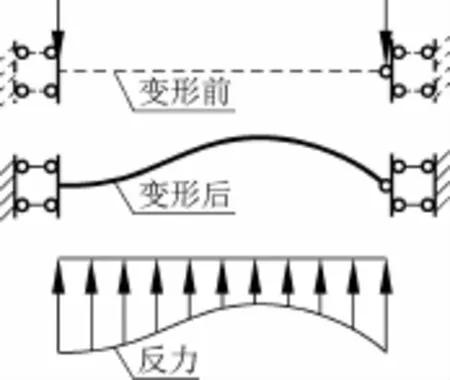
图1 基本设定示意Fig.1 Basic assumptions

2 内力计算

2.1 基本假定

1.板的计算模型

本文板采用的是弹性薄板，板放置于弹性地基上，板边受到一定约束，板长、宽方向为X轴、Y轴，板厚度方向为Z轴，板受到的边缘力与地基反力方向都平行于Z轴。

2.地基反力

地基反力分布服从Winkler模型如下：

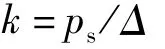
其中：k为基床系数（kN／m3）；ps为地基上任一点所受压力强度，与地基反力大小相等、方向相反（kN／m2）；Δ为对应点的沉降（m）。

3.边界条件

本文设定板放置于地基上，在竖向压力作用下板四边有着相同的竖向变形，没有水平位移。板的四边分为允许沿边线为轴转动，以及不允许沿边线为轴转动两种情况，这两种边界条件类似于弹性板的简支和固定边界，在本文中也把其分别叫做简支和固定。该边界条件不限制结构整体竖向变形，符合弹性地基理论要求。本文设定的这种边界条件，适用于周边有较高的壁板，且整体变形比较平均的水池底板分块简化计算。当壁板相对于底板较薄时可以近似认为底板边缘是简支的，当底板是跨度相近的连续板时可以近似认为板的边缘是固定的。

4.荷载

板的荷载是沿周边施加到板的法向上的，板面受法向的地基反力，与周边的荷载保持平衡。

在板面反力分布服从Winkler假定，边界变形服从等位移假定时，板周边荷载不一定均匀分布。表格编制时把周边的总荷载作为已知条件，考虑使用习惯，将这个总荷载除以板的面积作为弯矩计算参数。这个参数也可以理解为板面的平均地基反力，或名义均布反力。

2.2 计算方法

内力计算采用有限元法如下：把板分成n个结构单元，其中第i个单元的面积是Ai，地基反力压力强度为pi，地基反力在第i个结构单元引起的相对于板边的竖向变形为si，si也叫作板的局部变形，板的四边有均匀的变形s（见图4）。

定义p是名义均布反力，L是板的长度，W是板的宽度，根据p的定义及力的平衡条件有：

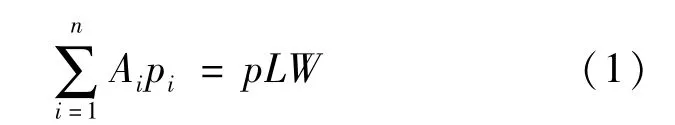
取地基上第i个单元竖向位移为Δi有：

按照Winkler地基模型且反力向上为正时有：变

换式（2）、式（3）后得到：

取：

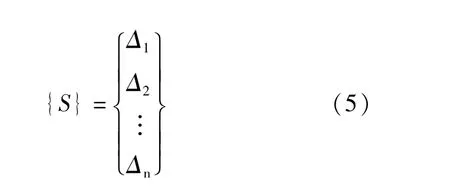
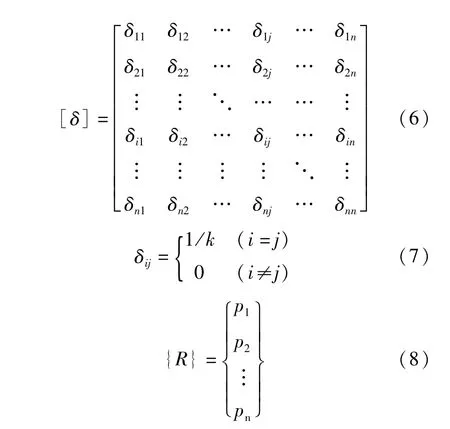
其中：［δ］为柔度矩阵；δij为沉降系数。

式（3）改写为向量形式得：

式（1）、式（2）、式（9）联立方程，方程以矩阵形式表达如式（10）所示：

其中，基床系数k、总反力pLW是已知量，局部变形si在初次计算时需假定一组初始值，在后续迭代计算时是已知量。边界的均匀变形s和各单元的反力pi是未知量。该方程组是线性方程组，方程个数与未知数相同，一般情况下，方程组有唯一解。解方程可求得各单元的反力pi。已知反力后，采用弹性有限元法可以求出新一轮变形和关键点的弯矩，继续迭代，一般情况下弯矩趋于收敛。

图2为板的局部变形示意，图3为地基反力示意，反力方向向上。

板相对于边缘的变形和相应的内力采用通用有限元软件计算，采用具有弯曲及薄膜特性的四边形弹性壳单元［3］，单元每个顶点有三个方向的旋转和位移共六个自由度，考虑分析简化，把板单元上的分布力折算到单元节点上，该点的集中力fi＝Aipi，取这一点的法向变形作为这个单元的变形si。单元长度、宽度均为板的长度的1／100。主要流程控制及线性方程组求解采用通用数学软件MATLAB［4］。初始变形采用名义均布反力作用下不允许周边竖向变形的相应边界条件下板的弹性变形。弯矩收敛的条件是前后两次迭代计算所得的弯矩差小于0.01%。

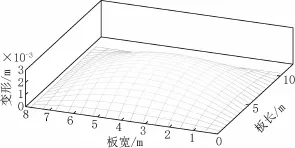
图2 板变形Fig.2 Deformation of the plate

2.3 计算过程

计算过程如下：

（1）步骤1：计算周边受常规约束的板在均布荷载条件下的变形作为变形的初值（图4a）；

（2）步骤2：根据地基变形（图4b）与反力（图4c）关系的假定，考虑荷载平衡条件以及边界条件解方程确定荷载的分布；

（3）步骤3：采用新的荷载分布按照周边约束的板进行计算，得到新的变形（图4d）；

（4）步骤4：比较每次计算得到的变形对应的弯矩与前次的差值，如果差值足够小，可以认为结果满足要求；若不满足，重复步骤2、3，最终所得的弯矩（图4e）作为计算结果。

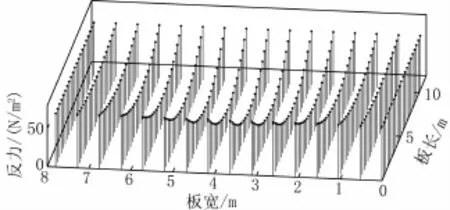
图3 地基反力Fig.3 Subgrade reaction

2.4 关于其他地基模型的讨论

上述计算方法也适用于其他地基模型上板的计算。改变地基柔度矩阵［δ］，就可以计算相应地基条件上的板的内力。式（11）是弹性半空间地基模型的地基柔度矩阵沉降系数δij的表达式［5］。

图4 迭代过程关键简图Fig.4 Key diagram of iterative process

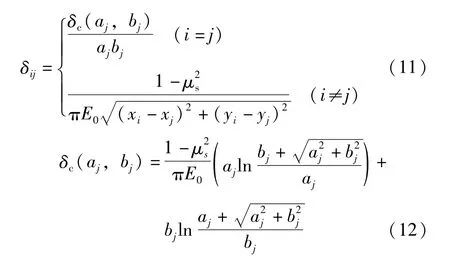
其中：E0为土的弹性模量；μs为土的泊松比；xi、yi为单元中心点的坐标；ai、bi为单元的边长。

同时，式（8）中pi的定义需要改为单元上的力，式（1）也要相应调整。

3 表格的组织

3.1 支座条件

对于不同支座条件需要采用不同的表格。常用的支座条件有四边简支、一边固定三边简支、邻边固定邻边简支、对边固定对边简支、三边固定一边简支、四边固定。

3.2 弹性特征值

定义板的弹性特征值［6］：

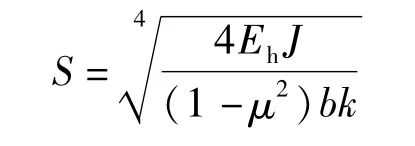
其中：Eh为板的弹性模量（kPa）；J为截面惯性矩（m4）；b为板的宽度，取1m；μ为板的泊松比，取0.2。

理论［6］和试算均显示，在其他条件不变的前提下，对于每种板厚、板的弹性模量及基床系数的组合，如果弹性特征值S相同，本文讨论的板的内力就相同。因此把弹性特征值S作为表格中的一个项目，在表格制作时对于每个S值选择一种组合进行计算。

3.3 荷载

Winkler模型的地基反力和变形满足线性条件，根据叠加原理，在适用范围内，荷载和弯矩具有线性关系，因此荷载不需要作为表格项目，只需要在计算公式中考虑。

3.4 板的长宽比

表格中还需要考虑矩形板不同的长宽比，因此板的长宽比应作为表格的一项。

3.5 板的尺寸

按照量纲分析，单位宽度弯矩M的量纲应该与单位面积的荷载q与边长L的平方的乘积相同。一般弹性板计算表采用式M＝mqL2计算板的弯矩，在长宽比确定的条件下，这里的m是一个与板的长度无关的常数。然而，对于Winkler地基上的板，在支座条件、弹性特征值、板的长宽比确定的条件下，参数m和边长的关系比较复杂。

图5为邻边固定邻边简支，弹性特征值为3m，长宽比为0.75的矩形板的跨中X方向单位荷载作用下的弯矩系数（mx）与边长（Lx）的关系。图5有两个反弯点，显然不是二次曲线关系。因此在表格其他项目确定的条件下，表中还必须列出不同边长与弯矩的关系。

在确定表格样式时，比较了两个方案。方案一是试图找到弯矩与边长之间的经验公式。形如mx＝aebLxLcx的表达式，当系数a＝-0.01207、b＝-0.1039、c＝2.507时，可以很好地拟合图5的曲线。但表格的不同位置有着不同的三个系数，表格比较复杂，量纲混乱，物理意义不明确。方案二是把不同长度下的弯矩系数都罗列出，使用时通过内插计算出相应的系数。方案一比较适于软件表达，方案二比较直观，本文给出的表格示列是按照方案二编制的。

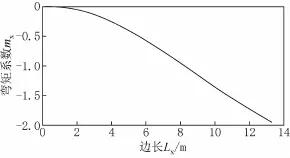
图5 边长与弯矩系数的关系Fig.5 The relationship between the length and themoment coefficient

周边加载条件下弹性地基上的板，当板的尺寸达到一定长度时，在板中部会出现0反力区，本表编制时，对每一种条件下板的尺寸上限进行了搜索，搜索条件是在迭代过程中板反力不出现0或改变方向的情况。另外迭代100次不收敛也认为超出了表的编制范围。本文所列表格中板长度的最大值，就是在对应条件下搜索得到的该方向最大边长尺寸。

4 表格编制和示例

4.1 表格形式

按照上述讨论，编制出了Winkler地基模型四边均匀沉降矩形板弯矩计算表。表格按不同边界条件共分为6张表格。每张表包含弹性特征值S从1m到6m共6种情况；按板的长宽比从0.25到3列出长宽比（对于对称性的支座条件只需要列出长宽比0.25到1的情况）；每种长宽比列出等差递减的5种长度的板的弯矩系数。

表格局部示列如表1、表2，相应的简图如图6、图7。表中参数：Lx、Ly为板尺寸（m）。

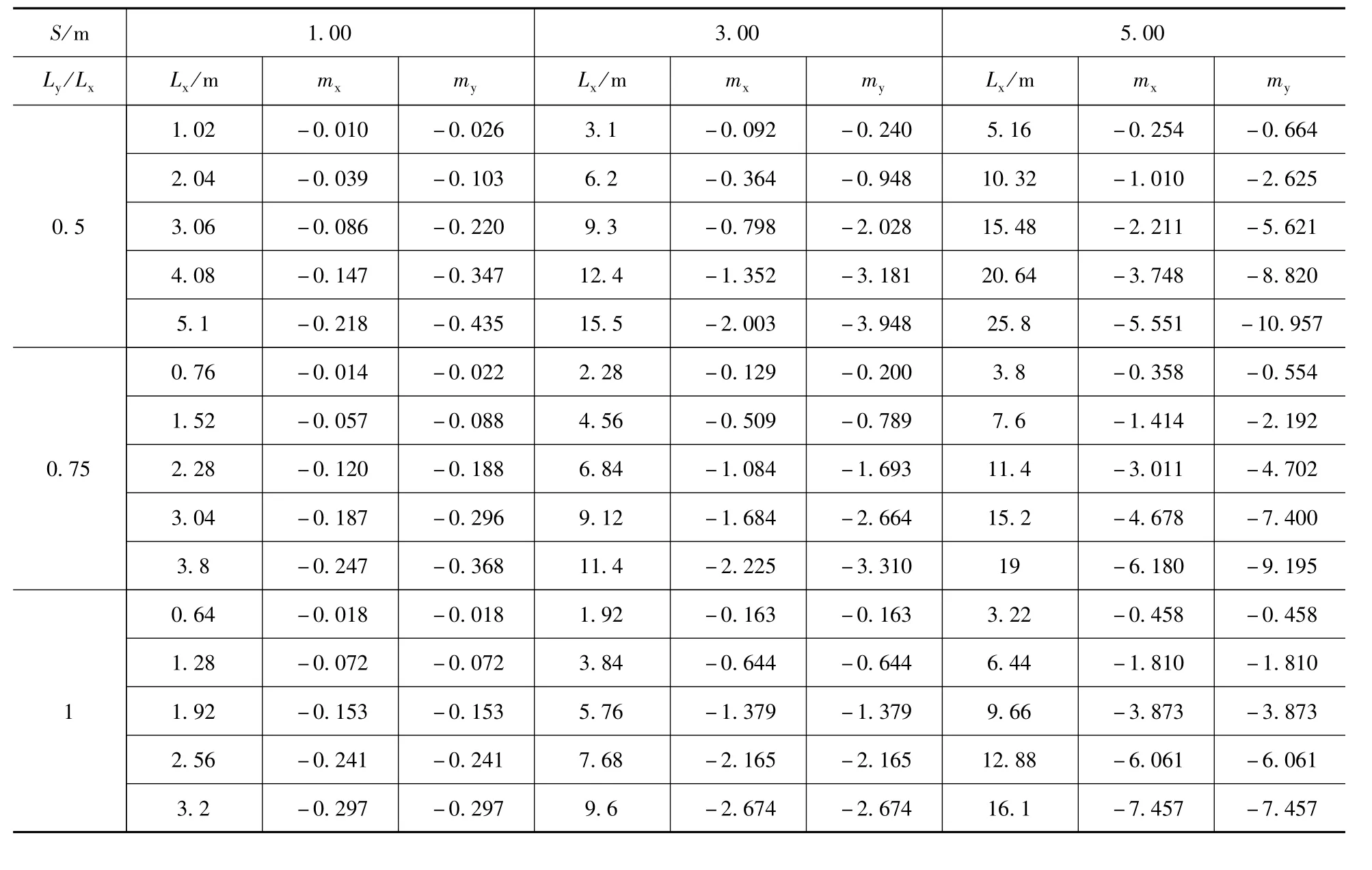
表1 W inkler地基模型四边均匀沉降矩形板弯矩计算表（四边简支）Tab.1 Table of bendingmoment of four-side uniform settlement rectangular plate of winklermodel（four sides simple supported）

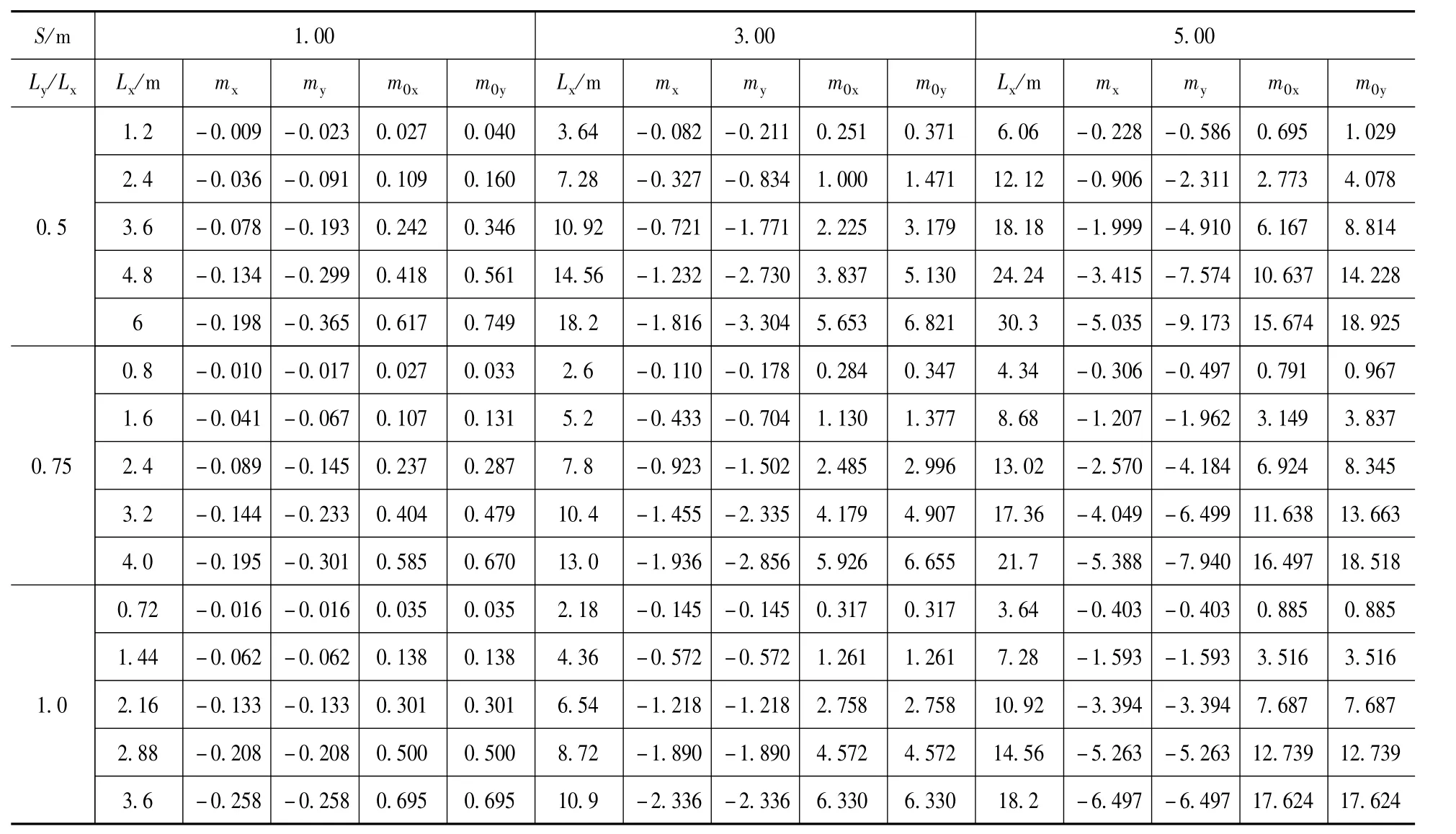
表2 W inkler地基模型四边均匀沉降矩形板弯矩计算表（邻边简支邻边固定）Tab.2 Table of bendingmoment of four-side uniform settlement rectangular plate of winklermodel（two adjacent sides simple supported and other two fixed）

图6 四边简支板简图Fig.6 Plate with four sides

图7 邻边简支邻边固定板简图Fig.7 Plates with two adjacent sides simple supported and other two fixed

板弯矩计算公式：Mx＝mxq式中：Mx为板Lx方向跨中计算弯矩最大值（kN·m／m，弯矩方向为纤维受拉、受压方向，下边受拉为正）；q为平均反力（kN／m2）。

其他位置弯矩My、M0x、M0y，以此类推，下标对应即可。

4.2 算例

已知条件如下：支撑条件：邻边简支邻边固定；混凝土板的弹性模量：3.0×107kPa；混凝土泊松比：0.2；板厚：538mm；基床系数：20000kN／m3；板长：10.4m；板宽：7.8m；平均净反力50kN／m2。计算简图如图8所示。

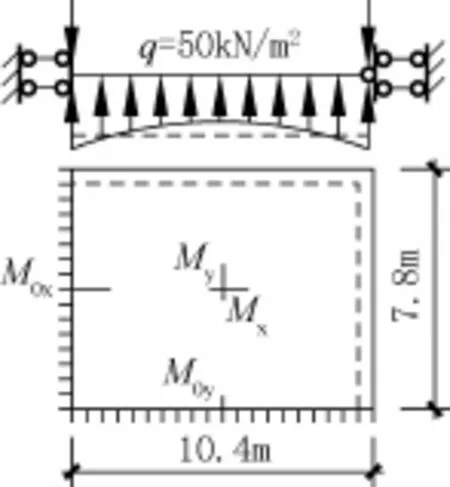
图8 算例计算简图Fig.8 Calculation diagram of examples

参数计算如下：

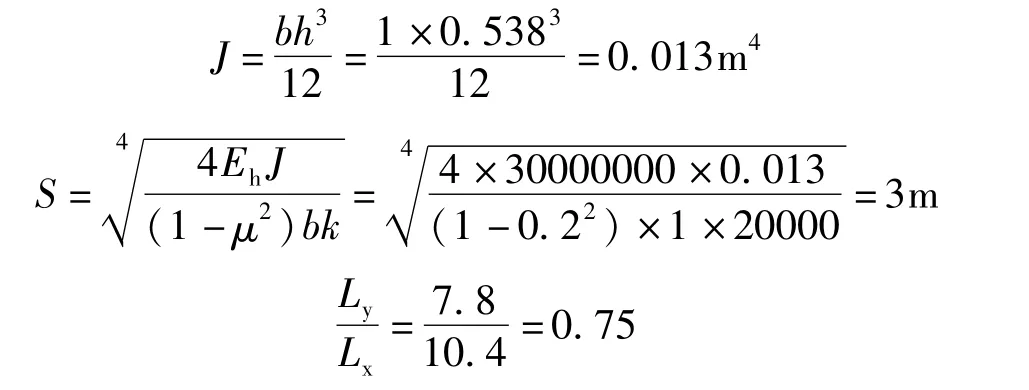
查表2得系数如下：mx＝-1.455、my＝-2.335、m0x＝4.179、m0y＝4.907。

计算得Winkler地基模型上板相应位置最大弯矩如下：

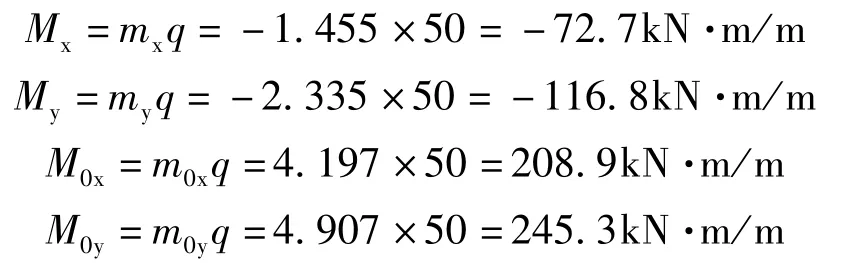
按照手册［3］普通弹性板表2.2.3-4计算，得相同支座条件均布荷载下板的相应位置最大弯矩如下：

按照式（11）的沉降系数表达式，取土的弹性模量为10.0MPa，土的泊松比为0.4，其余条件同本例，计算得半空间地基模型相应位置结果如下：

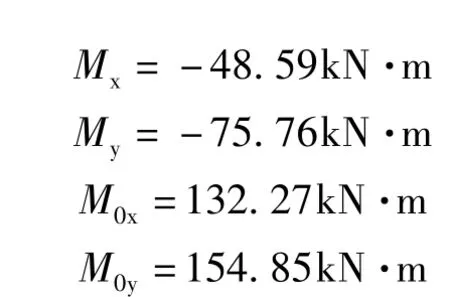
显然，底板考虑地基与土共同作用后，弯矩相对于按普通弹性理论计算的结果有所衰减。

5 结语

1.Winkler模型对土的假定以及对板刚度的假定与实际情况都有一定的误差，基床系数的取值也有很大的经验成分。但如果地基的可压缩土层较薄，与基础的最大水平尺寸相比为一个很薄的垫层，那就可以按Winkler假定来进行计算。在工程实际中，即使地基的可压缩土层较厚，也常常采用W inkler假定，因为计算比较简便，且相对刚性底板假定更符合实际情况。

2.本文的基本假定与实际水池底板受力状况具有近似性，计算过程中把分布力简化到节点上也有一定的系统误差，然而表格反应出的板与地基共同作用对底板弯矩的衰减规律是正确的。在基床系数合理取值，且扣除地下水影响的前提下，是能满足一般工程需要的。

3.在本文的假定条件下，边缘竖向力在板中引起的内力是否可以与边缘弯矩在板中引起的内力线性叠加，有待进一步研究。实际应用中，当水池矩形底板同时承受边缘竖向力和弯矩时，采用普通弹性板边缘弯矩在板中产生的弯矩与按本文计算表格得出的底板相应弯矩叠加，对于一般水池底板而言是偏安全的。

4.本文采用的基于通用有限元程序的迭代法具有概念清楚、使用方便等优点，通过调整柔度矩阵，可以适用于多种地基模型的计算。

5.本文讨论了在计算目标内力与边长之间相关性不明确的情况下，采用经验公式法及罗列法组织计算用表。在表格组织形式方面还有改进的余地，比如可以用其他的经验公式或用神经网路技术模拟内力与边长的关系。

［1］沈世杰，等.给水排水工程结构设计手册［M］.第2版.北京：中国建筑工业出版社，2007

［2］苏小卒，戴北山.弹性地基上矩形水池的计算及用表 ［J］.北京：特种结构，2003，20（4）：25-29 Su Xiaozu，Dai Beishan.Calculation and tables of rectangular pool on elastic foundations［J］.Beijing：Special Structures，2003，20（4）：25-29

［3］陈精一，蔡国忠.电脑辅助工程分析ANSYS使用指南［M］.北京：中国铁道出版社，1981

［4］苏金明，阮沈勇.MATLAB实用教程［M］.北京：电子工业出版社，2007

［5］华南工学院，南京工学院等.高等学校试用教程地基及基础［M］.北京：中国建筑工业出版社，2001

［6］中国船舶工业设计总公司第九设计研究院.弹性地基梁及矩形板计算［M］.北京：国防工业出版社，1983