基于一种新混沌电路的彩色图像加密方法
2018-05-11,,玉
, ,玉
(山东科技大学 电气与自动化工程学院,山东 青岛 266590)
随着现代通信技术的快速发展和影像传输要求的日益提高,信息安全尤其是图像信息的安全已成为通信领域的热点问题[1]。由于图像数据具有能量分布不均匀、数据量大、数据二维分布、原始数据存在大量冗余等特点,使得传统加密算法并不适合彩色图像加密[2]。混沌系统因其对初始条件的极度敏感性、伪随机性、遍历性等特点,在图像加密领域具有得天独厚的优越性。
近年来,基于确定混沌系统的彩色图像加密研究取得了一些重要的研究结果,Lang[3]利用颜色混合和分数阶傅里叶变换域中的混沌置换提出了一种加密算法;Wang等[4]基于两个复杂混沌系统,使用不同的置换、异或操作并结合多级加密结构提出了一种加密算法;Zhang等[5]基于Chen系统使用三维位矩阵置换并针对原图像的像素建立随机访问机制提出了一种加密算法;庹朝永等[6]基于二维Logistic映射,使用比特异或与随机重组并结合像素值的RGB重新分割提出了一种加密算法;卢辉斌等[7]基于自治三维混沌系统使用三维混沌序列的其中一维置乱图像RGB分量的像素位置,用另外两维序列设置置乱每个像素比特位的权值和阈值提出了一种加密算法;刘云等[8]基于三维Chen系统,使用行置乱及列置乱并结合折叠处理提出了一种加密算法。何松林[9]基于Logistic混沌序列,使用多个加密矩阵与基色矩阵进行多次异或并结合对RGB分量进行随机化处理提出了一种加密算法。邢丽坤等[10]基于混沌使用RGB分量分别加密并结合分数阶Fourier变换提出了一种加密算法。
密钥空间的大小是衡量加密安全性的一个非常重要的指标。与参数确定的混沌系统相比,具有电子元器件参数摄动的混沌电路,可以在原有的动力学特性中引入伪随机性[11],因此具有更丰富的动力学特性,这使得加密系统具有更大的密钥空间。参数摄动可视为电子元器件的固有属性,电子元器件的参数摄动因其变化过程非常复杂而不能用数学表达式加以描述,如果对确定的混沌电路引入电子元器件的参数摄动,可以在发送方和接收方进行保密通信。切换操作是一种重要的变换方法,在很多领域都有应用[12]。很多复杂的非线性动力学行为源自切换系统,因为通过切换操作可以很容易地获得小范围的参数摄动。而这些系统的动力学行为相较于其单个独立系统产生的动力学行为要复杂的多[13-15]。因此,在混沌加密系统中使用切换操作意义重大。混沌系统中使用切换操作的研究已有很多[16-22]。然而,这些研究主要集中在使用有限次的切换操作上。
本研究设计了新的混沌电路,该电路利用电子元器件的参数摄动和无限次的切换操作,获得更大的密钥空间。首先将一个绝缘栅型场效应管的漏极和源极与蔡氏电路中的线性电阻相串接,即实现将该场效应管的输出电阻与上述线性电阻相串联。通过利用混沌的遍历性来控制该场效应管的栅极和源极,使该场效应管的输出电阻呈现一个复杂的动态变化过程,最终使受驱动的蔡氏电路的等效线性电阻成为时变电阻。为了控制上述等效的线性电阻的变化范围,进而使该混沌电路具有更复杂的吸引子,特意设定一些元器件参数,并使用一些必要的电路来控制该场效应管的输入端电压的变化。仿真结果和安全性分析证实了基于本电路的加密方法的有效性和可行性。
1 新混沌电路的设计
蔡氏电路的动力学方程的表达式:
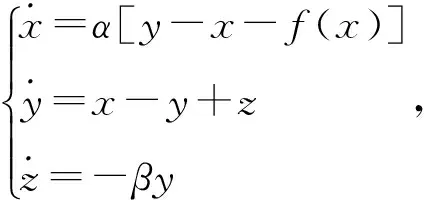
(1)
其中:
f(x)=bx+0.5(a-b)[x+1-x-1]。
(2)
式(1)是蔡式电路的状态方程去量纲后得到的动力学方程;式(2)是蔡式电路里的非线性电阻的伏安特性曲线对应的分段线性函数;式(2)的三段分别代表上述分段线性函数的三个组成部分,且是经过变量替换处理的。式(1)和式(2)中,α、β、a、b为固定不变的常量。
用电子仿真软件Multisim 12.0进行仿真,电路图如图1所示,其中(Ⅰ)部分为受驱动的蔡氏电路(左上角),(Ⅱ)部分为蔡氏激励电路(右下角)。绝缘栅型场效应管(2N6659)及其外围电路用以实现时变电阻的作用,具体为:首先利用混沌的遍历性控制该场效应管的栅极和源极,使得该场效应管的输出电阻呈现一个复杂的动态变化过程,然后将该场效应管的漏极和源极与受驱动的蔡氏电路中的线性电阻相串接,使得受驱动的蔡氏电路中的等效线性电阻变成时变电阻。为控制上述等效的线性电阻的变化,进而使该混沌电路具有更复杂的吸引子,将蔡氏激励电路的变量y选作原始激励变量,借助绝对值电路和同相加法电路来最终控制场效应管的输入回路。电路元器件参数为:R1=R17= 1.7 kΩ,R2=R19= 2.2 kΩ,R3=R4=R18=R20= 0.2 kΩ,R5=R7=R21=R22= 22 kΩ,R6=R23= 3.3 kΩ,R8= 9.981 kΩ,R9= 1 kΩ,R10=R11=R12=R14=R15=R16= 100 kΩ,R13= 25 kΩ,C1=C3= 100 nF,C2=C4= 10 nF,L1=L2= 18 mH,V1= 500 mV,运放是TL082CD,模拟乘法器是AD633。受驱动的蔡氏电路仿真图如图2所示。
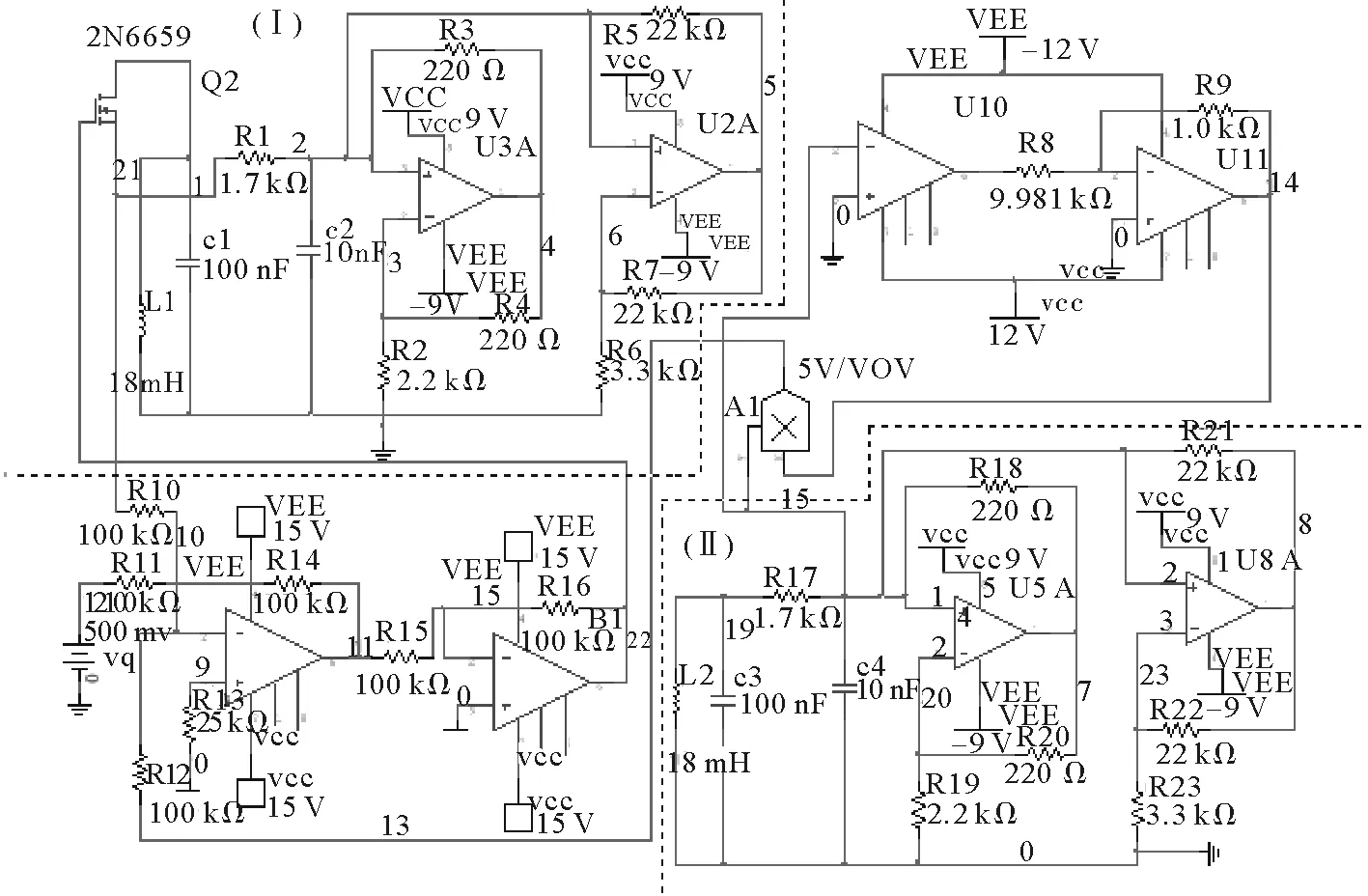
图1 新混沌电路的电路图Fig.1 Circuit diagram of new chaotic circuit
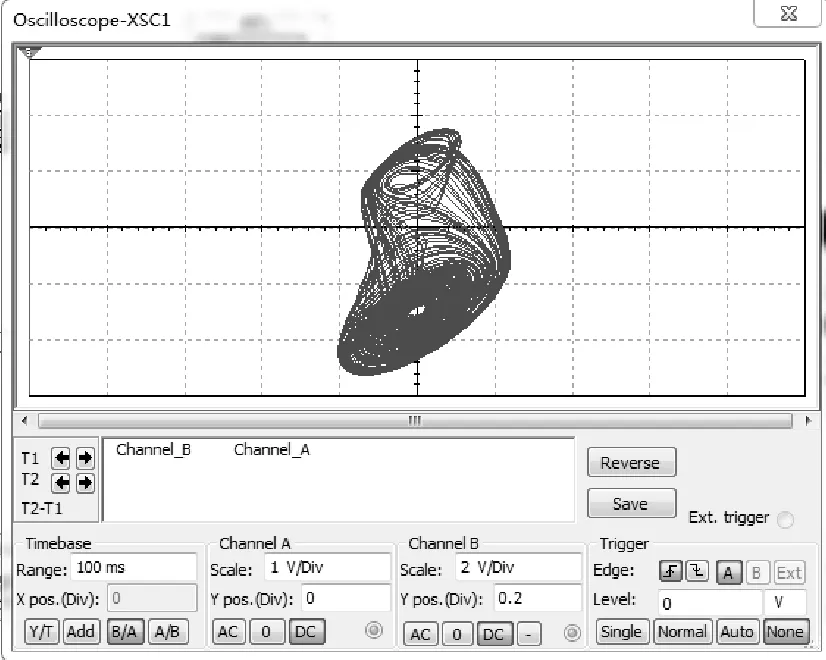
图2 新混沌电路状态变量x和y的相图Fig.2 Phase portraits of state variables x and y
2 加密方案
本加密算法利用新设计的混沌电路产生密钥流,用像素置乱和替代相结合的方法对原始图像进行加密。其中,像素置乱用以扰乱原始图像的像素位置,降低相邻像素间的相关性;像素值替代用于改变置乱后图像的像素灰度,扰乱图像的统计特性。
2.1 混沌加密序列的产生
通过对受驱动的蔡氏电路的状态变量x和y的采样,分别得到两组混沌序列{xn}、{yn}。这两组混沌序列经过处理后将用来完成对彩色图像的R通道的加密。通过改变受驱动的蔡氏电路的线性电阻R1的阻值,得到了用于对彩色图像的G、B通道进行加密的另外四组混沌序列。其中,用于对R通道进行加密所用的阻值是1.70 kΩ,对G、B通道进行加密所用的阻值分别是1.72和1.75 kΩ。本文对R通道的加密过程进行介绍,G、B通道加密过程和R通道的相同。
2.2 加密步骤及仿真结果
Step 1:读入彩色图像的R通道Amn,1≤i≤m,1≤j≤n,m和n分别是图像的高度和宽度,将矩阵A按列拉直并得到序列Ln×m{l1,l2, …,ln×m};
Step 2:对混沌序列{xn}、{yn}进行截取,使之与序列Ln×m等长;
Step 3:对经过截取得到的新的混沌序列{xn}、{yn}进行预处理,将其均变为整数序列,且上述整数序列位于区间 [0, 255] 内。计算公式分别如下:
Xn=abs(Xn/max(|Xn|)×255),
(3)
Yn=mod(abs(fix((Yn-fix(Yn))×103)),256)。
(4)
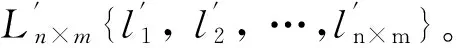
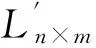
使用大小为200×200的彩色图像“Lena”作为明文图像,利用Matlab R2013b软件进行仿真。仿真结果如图3~4所示。

图3 仿真图像Fig.3 Images used in the simulation

(a)-(c)明文图像R、G、B通道的灰度图;(d)-(f) 密文图像R、G、B通道的灰度图
图4明文图像和密文图像各个通道的灰度图
Fig.4 Gray images of each channel of the plain image and encrypted image
3 安全性分析
3.1 灰度分布直方图对比
直方图通过统计不同像素的个数,可以反映图像像素值的分布规律。直方图分布越均匀,则说明图像像素值分布越无规律可循,从而有效防止攻击者从统计特性方面获取有效信息。原始图像和加密图像各个通道的直方图如图5所示。通过对比可以看出,原始图像的像素值集中分布在某些点,而加密图像的像素值则是均匀分布。即原始图像经过加密处理后,在对抗潜在的统计攻击时具有较高的安全性。
(a)-(c)原始图像R、G、B通道的直方图;(d)-(f)加密图像R、G、B通道的直方图图5 原始图像和加密图像各个通道的灰度分布直方图Fig.5 Histograms of plain image and encrypted image in each channel
3.2 相关性分析
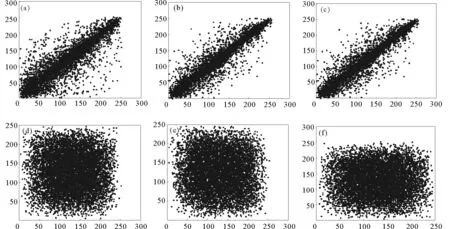
通过每次随机选取10 000对相邻的像素值,分别计算原始图像和加密图像在水平方向、垂直方向和对角线方向的相关系数。计算公式如下:
(5)
(6)
(7)
(8)
其中:x和y分别表示两相邻像素的灰度值,p为图像的总像素个数,pxy为相邻像素的相关系数。
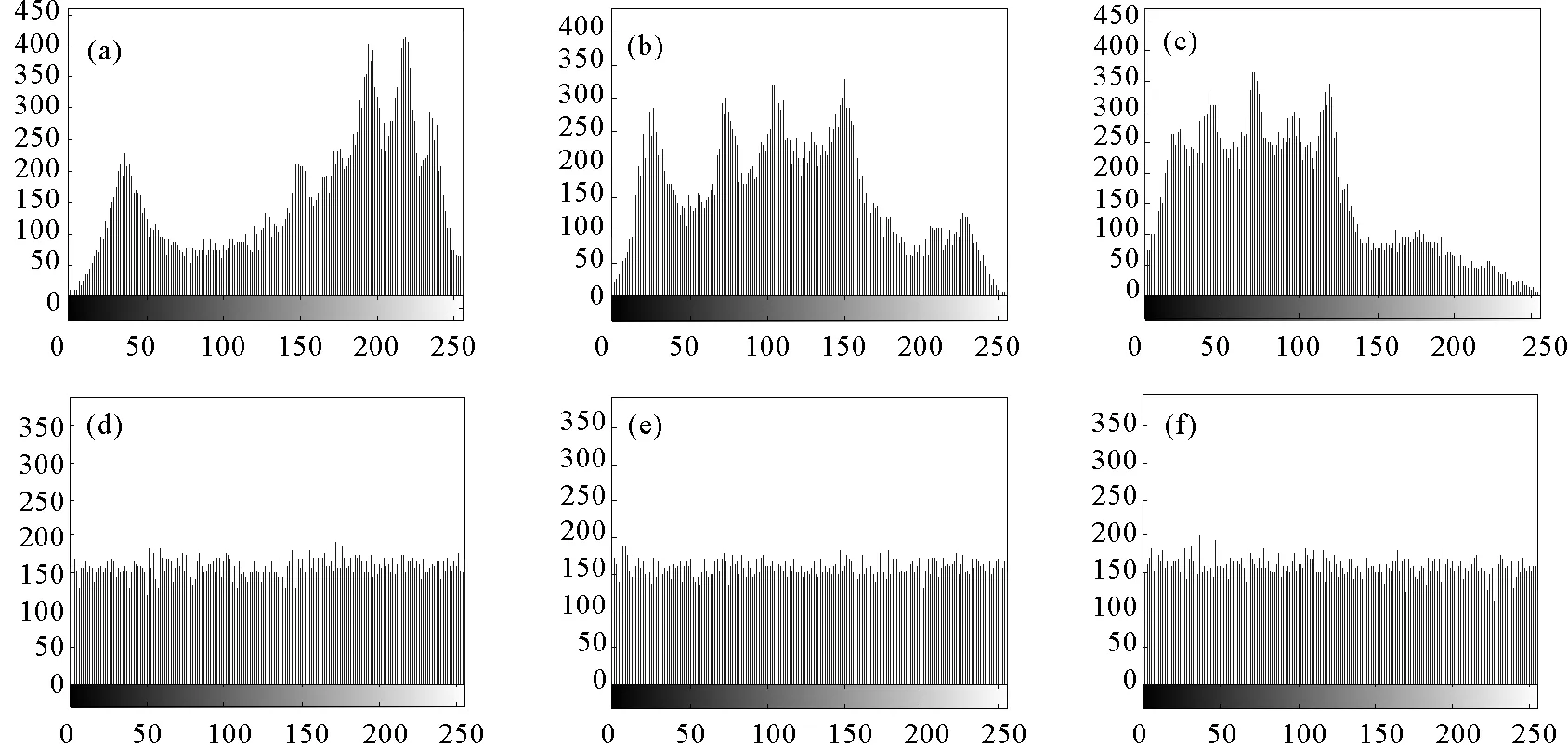
仿真结果如图6和表1所示。通过对比可知,原始图像相邻像素的相关性非常大,而加密图像相邻像素的相关性却非常小,说明原始图像的统计特征已完全被随机分散,即无法检测到原始图像和加密图像之间的相关性。
3.3 信息熵分析
信息熵的计算公式为:
(9)
其中:n表示图像的灰度等级,pi表示灰度值为i的像素出现的概率。
(a)-(c)原始图像水平、垂直、对角线方向相邻像素相关性;(d)-(f)加密图像水平、垂直、对角线方向相邻像素相关性图6 原始图像和加密图像各个方向的相邻像素相关性Fig.6 Correlations of plain image and encrypted image in every directions
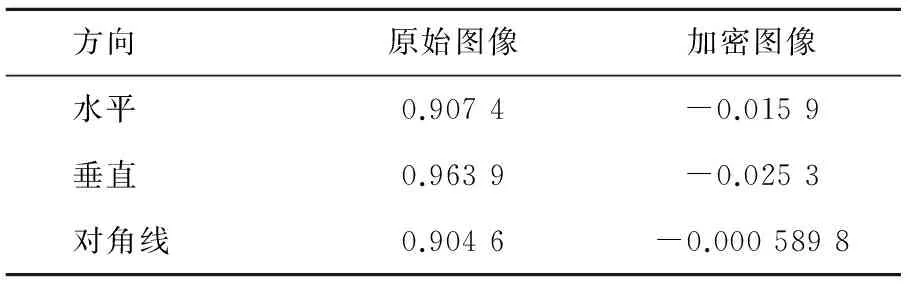
方向原始图像加密图像水平0.9074-0.0159垂直0.9639-0.0253对角线0.9046-0.0005898

表2 加密图像的信息熵Tab.2 Information entropies of encrypted image
由于所用原始图像的灰度等级是256,即信源的符号数是256,那么该信源的理想熵值为8。图像的熵值越接近8,则图像的灰度分布越均匀。仿真结果如表2所示,结果表明:密文图像的各个通道的信息熵均非常接近8,即密文图像的各个通道的灰度分布中可用的明文信息非常少。
3.4 密钥空间和密钥灵敏度分析
提出的新混沌电路的密钥空间理论上可为无穷大。
加密所用的混沌序列的的原理可分为如下几步:
第一步:本方法通过对蔡氏电路的动力学轨道进行采样,得到一有限长时间序列{an}。然后将蔡氏电路的线性电阻由1.70 kΩ 改为1.92 kΩ,并得到另一有限长时间序列{bn}。通过将序列{an}的前t1个项和序列{bn}的第t1+1项到第2t1项组合起来得到序列{cn}。原理图如图7所示。
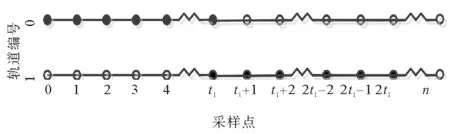
图7 产生组合混沌序列的原理图Fig.7 Schematic diagram of the combination of chaotic sequence
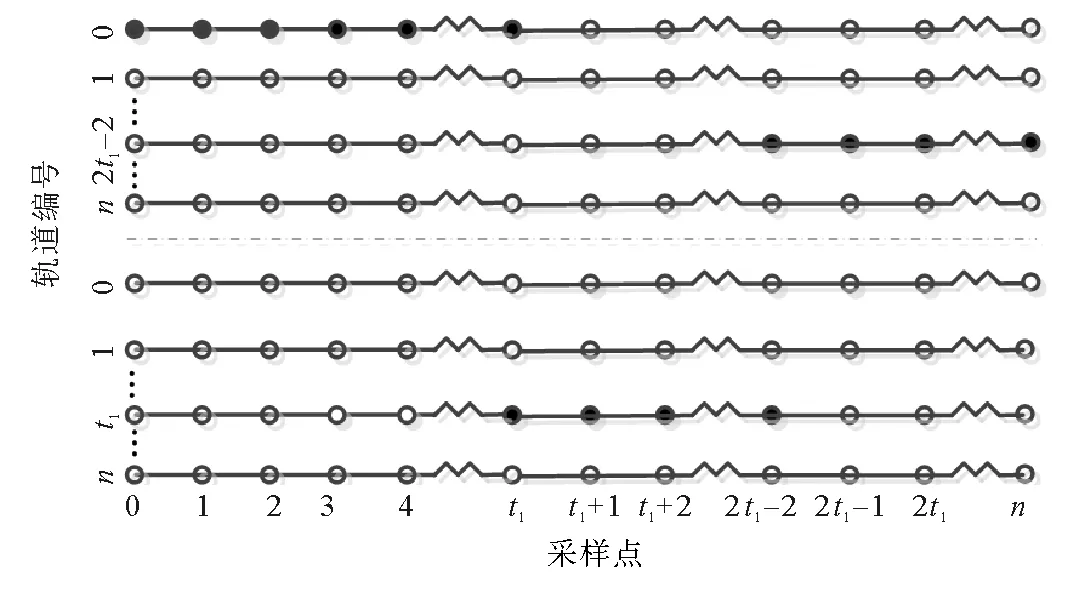
图8 新蔡氏电路产生混沌序列的原理图Fig.8 Schematic diagram of the chaotic sequence for new Chua’s circuit
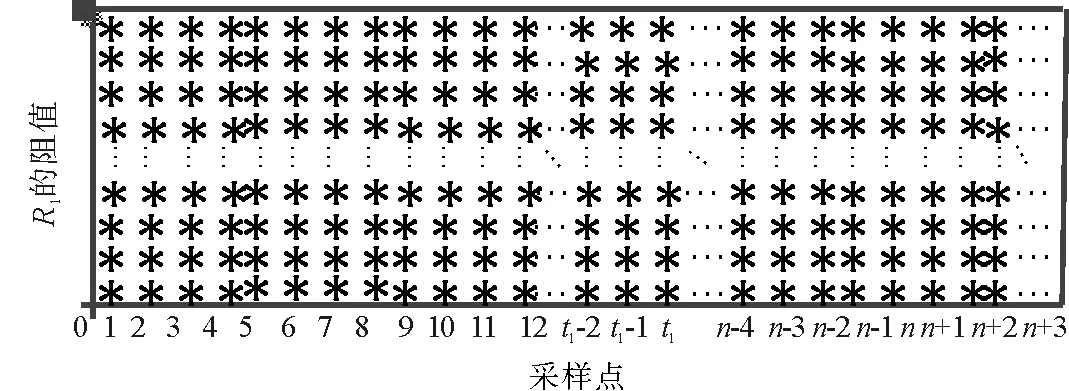
图9 新混沌电路产生混沌序列的原理图Fig.9 Schematic diagram of the chaotic sequence of the new chaotic circuit
图7中轨道编号0:R1=1.70 kΩ,初始状态为(x0,y0);轨道编号1:R1=1.92 kΩ,初始状态为(x0,y0)。
第二步:基于有限次切换操作的新蔡氏电路的混沌序列的原理图,如图8所示。
图8中轨道编号n:初始状态为(xn,yn)的轨道;点划线:R1阻值分界线,线上部分为1.70 kΩ、线下部分为1.92 kΩ。初始时刻,系统在蔡氏电路(其线性电阻R1阻值为1.70 kΩ)处于初始状态为(x0,y0)时的轨道上演化;t1时刻进行切换,R1阻值变为1.92 kΩ,系统开始在蔡氏电路处于线性电阻阻值为1.92 kΩ、初始状态为(xt1,yt1)时的轨道上演化;2t1-2时刻进行第二次切换,R1阻值变为1.70 kΩ,系统开始在蔡氏电路处于线性电阻阻值为1.70 kΩ、初始状态为(x2t1-2,y2t1-2)时的轨道上演化。
第三步:本算法中新混沌电路产生混沌序列的主原理图如图9所示。系统的轨道离开初始状态点后,受驱动蔡氏电路的线性电阻的阻值就开始在有限范围内时刻变动且变化过程复杂,故而接下来的每一时刻,轨道都在进行切换且可能切换到整个轨道范围里的任一轨道之上。考虑初始状态的情况,就是将上述每一轨道按照图8中的方式扩展为n条轨道,即系统轨道离开初始状态点后的每一时刻,轨道都在进行切换且可能切换到对应于蔡氏电路处于线性电阻阻值为有限范围内任一值、初始状态为无数状态中某一特定状态时的轨道。而且,通过设定相关参数使得系统的状态点始终是从一个双涡卷混沌吸引子的轨道跳到另一个双涡卷混沌吸引子的轨道上。
鉴于混沌系统是非线性系统,元器件参数的小范围摄动对混沌系统动力学特性的影响与切换操作对混沌系统动力学特性的影响并非是简单的线性叠加。相反,二者结合在一起,时刻都在共同发挥作用。即此时元器件参数的小范围摄动对系统动力学特性的影响已不可忽视。
为了分析密钥灵敏度,仅将图1中受驱动蔡氏电路的虚拟线性电阻R1的阻值由1.700 000 000 0 kΩ变为1.700 000 000 1 kΩ,保持软件Multisim 12.0里相关仿真参数的一致,并按照产生原混沌加密序列的操作过程进行操作,最终得到对应的新的混沌加密序列{Xn2}、{Yn2}。仿真结果如图10所示。
由仿真结果可知,使用错误的密钥进行解密得到的图像完全不同于原始图像,即解密算子即使仅有10-10的偏差,解密将完全失败。可见此加密算法足以对抗枚举攻击。

(a)原始图像;(b)正确密钥解密的图像;(c)错误密钥解密的图像图10 原始图像和解密图像Fig.10 Plain image and decrypted images
4 结论
基于电子元器件的参数摄动和实时切换操作设计了一种新混沌电路,对彩色图像进行加密。通过引入时变电阻使得该混沌电路相较于确定的混沌加密系统拥有更好的伪随机性,大大提高了加密的安全性。此外,基于上述新混沌电路的加密系统,在保证安全性能的前提下,使用更加简单的加密算法且易于编程实现。由于电路通常是基于标准元器件来实现的,因此混沌电路器件定型和必要的外围电路的设计需要综合考虑多方面因素,具备一定的电路方面的先验知识可以很好地解决上述问题。总之,新混沌电路在通信系统保密性方面具有潜在的应用价值。仿真结果说明了新混沌电路的正确性、加密方法的有效性。
参考文献:
[1]朱和贵.信息安全中混沌图像加密算法及其相关问题研究[D].长春:吉林大学,2014.
[2]何希平.基于混沌的图像信息安全算法研究[D].重庆:重庆大学,2006.
[3]LANG J.Color image encryption based on color blend and chaos permutation in the reality-preserving multiple-parameter fractional Fourier transform domain[J].Optics Communications,2015,338:181-192.
[4]WANG L Y,SONG H J,LIU P.A novel hybrid color image encryption algorithm using two complex chaotic systems[J].Optics and Lasers in Engineering,2016,77:118-125.
[5]ZHANG W,YU H,ZHAO Y L,et al.Image encryption based on three-dimensional bit matrix permutation[J].Signal Processing,2016,118:36-50.
[6]庹朝永,秦拯,黎谦.联合二维 Logistic 混沌映射与比特重组的彩色图像加密算法[J].计算机科学,2013,40(8):300-302.
TUO Chaoyong,QIN Zheng,LI Qian.Color image encryption algorithm based on 2D logistic chaotic map and bit rearrange [J].Computer Science,2013,40(8):300-302.
[7]卢辉斌,王丽佳.基于 Hopfield 网络的彩色图像混沌加密算法[J].吉林大学学报(信息科学版),2014,32(2):131-137.
LU Huibin,WANG Lijia.Color image encryption algorithm of chaotic based on the Hopfield network[J].Journal of Jilin University (Information Science Edition),2014,32(2):131-137.
[8]刘云,郑永爱,基于混沌系统的彩色图像加密新方案[J].计算机工程与应用,2011,47(3):90-93.
LIU Yun,ZHENG Yong′ai.Novel encryption scheme for color image based on chaotic system[J].Computer Engineering and Applications,2011,47(3):90-93.
[9]何松林.基于混沌序列的数字彩色图像加密算法[J].计算机工程,2011,37(10):114-116.
HE Songlin.Encryption algorithm for digital color image based on chaotic sequences[J].Computer Engineering,2011,37 (10):114-116.
[10]邢丽坤,华正春,牛秀龄,等.基于混沌和 FRFT 的彩色图像加密算法[J].电脑知识与技术,2016,12(12):201-203.
XING Likun,HUA Zhengchun,NIU Xiuling,et al.Color image encryption algorithm based on chaos and FRFT[J].Computer Knowledge and Technology,2016,12(12):201-203.
[11]VATS V B,PARTHASARATHY H.A perturbation-based model for rectifier circuits[J].International Journal of Differential Equations,2006(3):1-13.
[12]LI Q L,LIU H J,SONG X K,et al.Modeling and stability analysis of three-phase converter based on switching system theory[J].Transactions of China Electronical Society,2009,24:89-95.
[13]ZHANG Z,BI Q.Bifurcation in a piecewise linear circuit with switching boundaries[J].International Journal of Bifurcation and Chaos,2012,22(2):1-18.
[14]GARDINI L,FOU RNIER-PRUNARET D,CHARGE P.Border collision bifurcations in a two-dimensional piecewise smooth map from a simple switching circuit[J].Chaos:An Interdisciplinary Journal of Nonlinear Science,2011,21(2):023106-023118.
[15]BORAH M,SINGH P P,ROY B K.Improved chaotic dynamics of a fractional-order system,its chaos-suppressed synchronization and circuit implementation[J].Circuits,Systems,and Signal Processing,2016,35(6):1871-1907.
[16]WANG B,ZHONG S M,DONG X C.On the novel chaotic secure communication scheme design[J].Communications in Nonlinear Science and Numerical Simulation,2016,39:108-117.
[17]RODRIGUES V P,OLIVEIRA T,CUNHA J P.Globally stable synchronization of chaotic systems based on norm observers connected in cascade[J].IEEE Transactions on Circuits and Systems II:Express Briefs,2016,63(9):883-887.
[18]ZEMLYANYI O V.Keying of the broadband chaotic signal spectrum for data transmission[J].Telecommunications and Radio Engineering,2016,75(5):401-411.
[19]HUANG L L,ZHANG J,SHI S S.Circuit simulation on control and synchronization of fractional order switching chaotic system[J].Mathematics and Computers in Simulation,2015,113:28-39.
[20]MA T.Synchronization of multi-agent stochastic impulsive perturbed chaotic delayed neural networks with switching topology[J].Neurocomputing,2015,151:1392-1406.
[21] GAO X,XIE F,HU H.Enhancing the security of electro-optic delayed chaotic system with intermittent time-delay modulation and digital chaos[J].Optics Communications,2015,352:77-83.
[22] HSU W T,TSAI J S H,GUO F C,et al.From fault-diagnosis and performance recovery of a controlled system to chaotic secure communication[J].International Journal of Bifurcation,2014,24(12):1-30.
