基于插值的非等间距GM(1,1)建模方法
2018-05-11,,
,,
(山东科技大学 测绘科学与工程学院, 山东 青岛 266590)
因灰色系统具有通过“贫信息”就能对未知数据进行挖掘的能力[1-3],其问世的30多年来,灰色预测模型(grey model,GM)已经在各个领域得到了广泛的应用[4]。但是由于均值GM(1,1)模型仅适用于等间距序列,而在实际应用中得到的数据序列往往都是不等间距的。为了解决这个问题,众多学者针对不等间距GM(1,1)模型进行了研究[5-13],并将其应用从单点或单一变量拓展到多点或多个变量[14-16]。李斌等[5]将非等间距序列根据时间间隔构造出等间距序列进行预测,再根据时间间隔还原为原始序列的预测值,验证了GM(1,1)模型用于沉降数据分析的实用性、有效性和正确性。Shen[6]通过梯形公式和中心差商法得到灰导数的白化值,提出一种基于最小误差平方和准则的非等间距序列建模方法,结果表明该模型的拟合与预测精度显著提高。李翠凤等[10]通过插值优化非等间距模型的背景值,增强背景值的适应性,提高非等间距序列的预测精度。尹晖等[14]将彼此关联的多个变形点进行整体建模,采用非等间距等距化处理的改进方法,验证了非等间距多点变形预测模型的可行性和有效性。
对于非等间距GM(1,1)模型的改进,无论是单一序列预测或多个相关序列预测,目的都在于提高模型的预测精度。本文基于非等间距的变形观测序列,建立两个模型,采用插值将其构造成等间距序列,其中一个模型采用文献[10]的方法对新序列背景值进行优化,另一个模型采用均值GM(1,1)模型的背景值选取方式,分别预测出新序列的预测值,最后再进行一次插值还原为原始非等间距序列的预测值。为验证该改进模型的有效性,采用文献[5]中的实例进行对比分析,结果证明本文中的变形预测改进模型的预测精度更高。
1 均值GM(1,1)模型
1.1 均值GM(1,1)模型的建立
设有非负等间距非负序列:
X(0)={x(0)(k)|k=1,2,…,n}。
(1)
作X(0)的1-AGO序列得到:
X(1)={x(1)(k)|k=1,2,…,n},
(2)
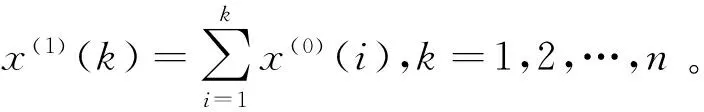
通过X(1)构造该模型的背景值:
Z(1)={z(k)|k=1,2,…,n},
(3)
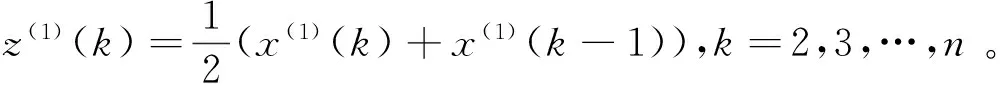
x(0)(k)+az(1)(k)=b,
(4)
称为GM(1,1)模型的均值形式。其白化微分方程为:
(5)
(6)
式中,Y,B分别为:
(7)
借助白化微分方程的解构造均值GM(1,1)的时间响应式:
(8)
再作累减,还原预测值:
x(0)(k)=x(1)(k)-x(0)(k-1),k=2,3,…n。
(9)
1.2 模型检验
通过均值GM(1,1)模型得到预测值序列:
(10)
构成残差序列:
e={e(k)|k=1,2,…n},
(11)
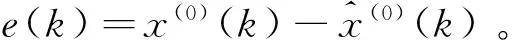
残差表示预测值相对于原始数据的偏离程度,偏离程度越小,说明预测的精度越高,反之预测的精度越低。根据残差序列计算每一期数据预测的相对误差,进而得出预测的平均相对误差:
(12)
(13)
相对误差表示每一期预测的误差大小,相对误差越小,精度越高,反之越低;平均相对误差表示该预测序列的误差大小,平均相对误差越小,预测精度越高,反之越低。
2 非等间距GM(1,1)建模改进
主要采用插值的方式对GM(1,1)模型进行改进,建立两种不同的模型进行对比试验。但插值方法种类繁多,各种插值方法对特定序列的插值准确程度差异显著,故在对某一特定序列进行灰色预测,应先对各个插值模型进行试验对比,选择适合该序列的方法进行预测。
2.1 方法一
均值GM(1,1)适用于等间距序列,但对于非等间距的序列预测精度较差。如图1所示,由于间距ki+1-ki≠ki+2-ki+1,故其不适用于均值GM(1,1)模型。对图中曲线进行插值,便可得到新的等间距序列(14),以满足通过均值GM(1,1)模型进行预测的要求。
X′(0)={x(0)(k′)|k′=1,2,…,n}。
(14)
通过均值GM(1,1)模型对等间距序列(14)进行预测,得到该序列的预测值,进而再对该预测序列值进行插值,还原得到原始非等间距序列的预测序列。
2.2 方法二
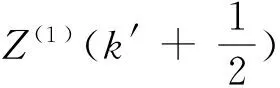
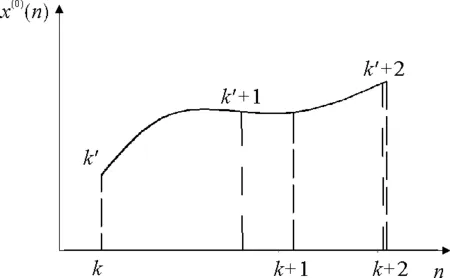
图1 等间距插值Fig.1 Equidistant interpolation
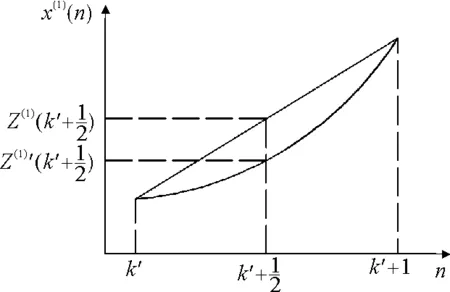
图2 背景值插值Fig.2 Background value interpolation
3 实例分析
为对两个预测模型进行检验,采用文献[5]中的观测数据进行试验对比。观测点的布设如图3所示。
选取南侧地表D15点的沉降值作为时间序列进行预测检验,该点共有10期非等间距的沉降观测数据。选取该观测数据中的前8期为已知数据进行建模,对后两期数据进行预测,分析对比预测精度。D15点的观测资料如表1所示。
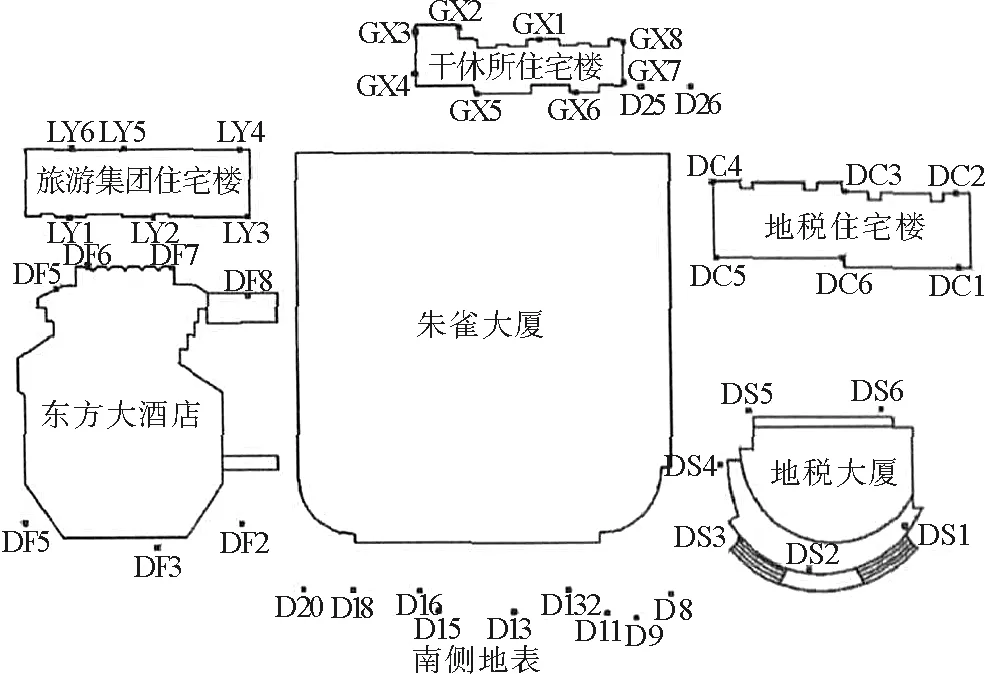
图3 地表沉降点点位布设图Fig.3 Location map of surface subsidence
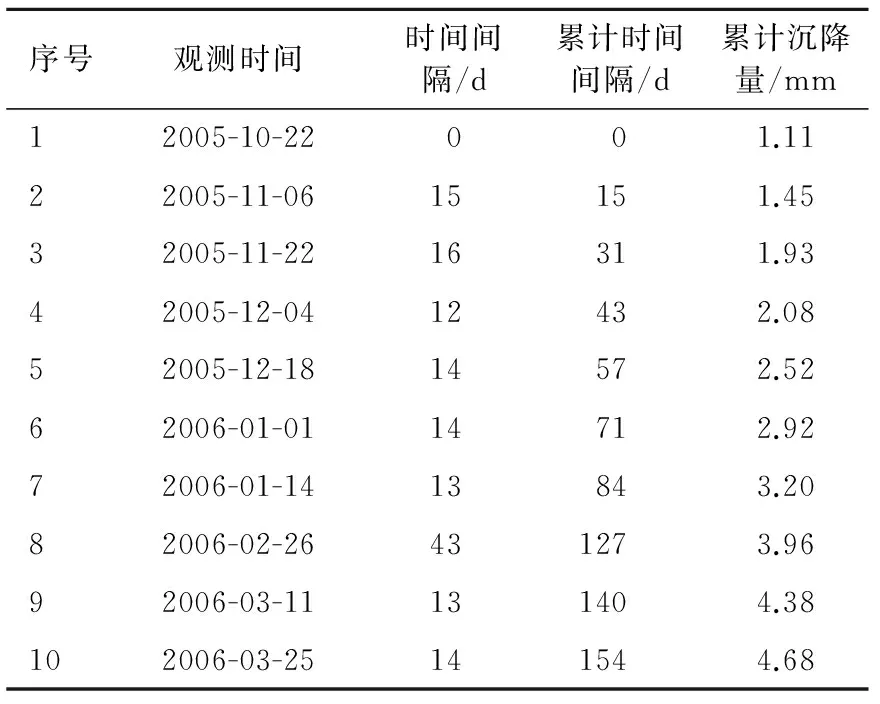
序号观测时间时间间隔/d累计时间间隔/d累计沉降量/mm12005-10-22001.1122005-11-0615151.4532005-11-2216311.9342005-12-0412432.0852005-12-1814572.5262006-01-0114712.9272006-01-1413843.2082006-02-26431273.9692006-03-11131404.38102006-03-25141544.68
首先进行插值方法的选取。分别用分段线性插值、邻近点插值、三次样条插值和三次多项式插值对前8期数据进行插值,插值点间隔为10,插值点区间从0到300。各个插值方法的插值曲线如图4所示。
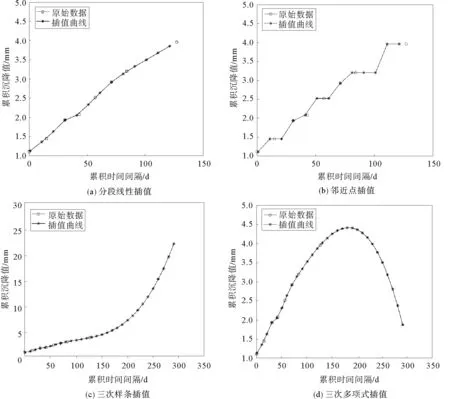
图4 插值曲线图Fig.4 The interpolation curve
从图中可以看出,分段线性插值并不圆滑,但对较为稠密的序列适用,在序列外的点不能得到其函数值;邻近点插值显然并不适用于该序列的插值计算;三次样条插值和三次多项式插值曲线比较圆滑,但对于沉降数据而言,累计沉降值总是在不断增大,显然三次多项式插值对于沉降观测数据而言并不适用,故选取三次样条插值方法。
采用三次样条插值法结合前文两种方法对文献[5]中的前8期观测数据进行拟合并预测出后两期数据,并将其与文献[5]中的预测结果进行对比,如表2所示。计算每种预测方法的相对误差及平均相对误差,如表3所示。并分别绘制预测值对比图与残差值对比图,如图5、图6所示。
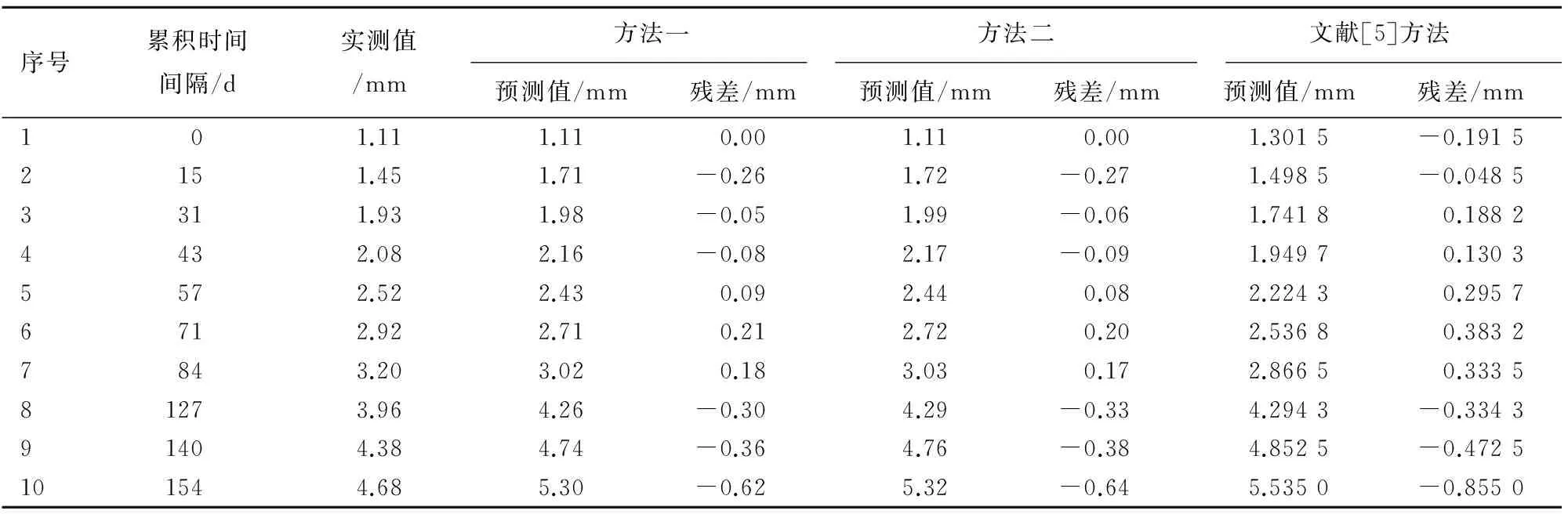
表2 预测结果对比
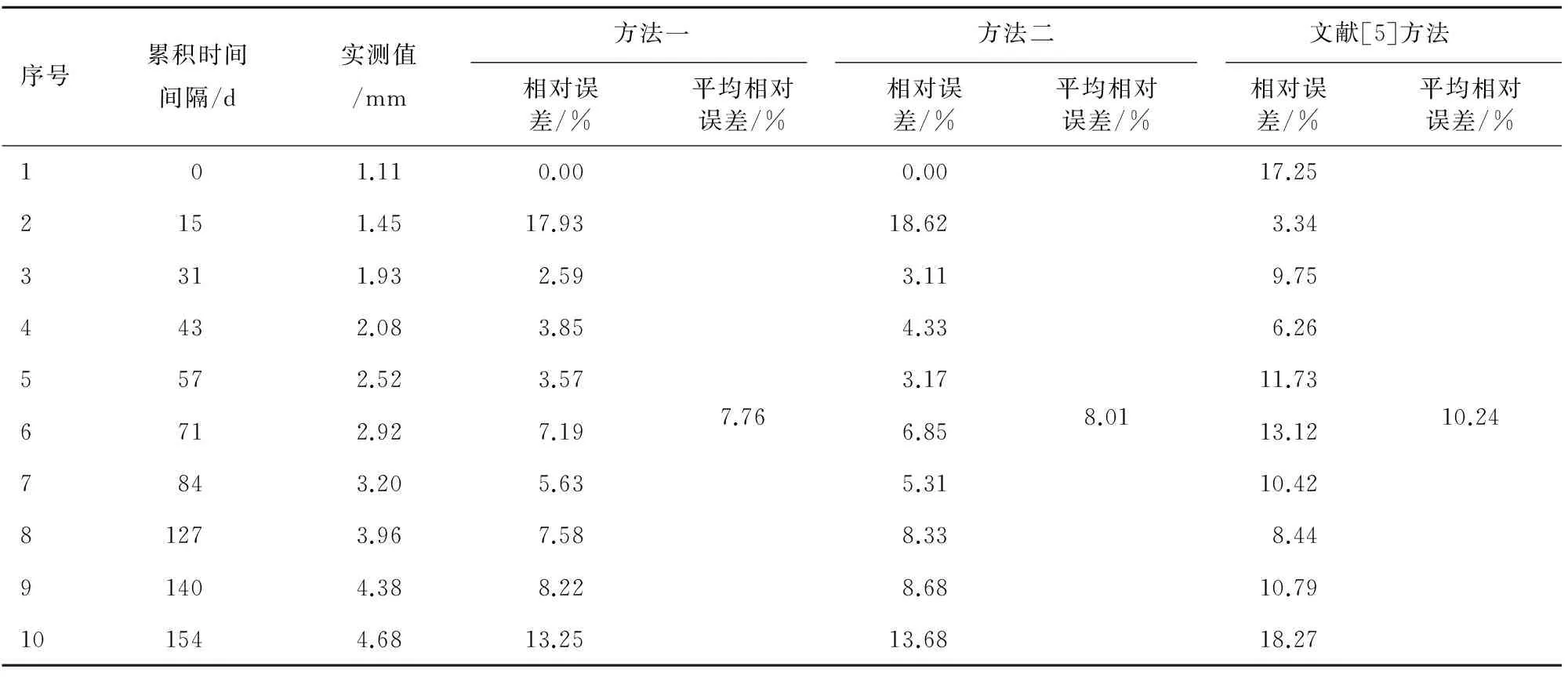
表3 误差对比
从表2和图5中可以看出,相比于文献[5]中的方法,运用本方法一和方法二进行预测,所得的预测值更加接近实测值,并且图6中的残差图以及表3中的平均误差与相对误差也很好地说明了这一点,证明了本文两种预测模型的有效性及实用性。
对比方法一和方法二可以看出,虽然其预测精度非常接近,但不通过插值进行背景值的优化比采用插值进行背景值优化的误差更小,说明了在该观测序列下,多次进行插值处理会在一定程度上降低预测的精度。
另外,图6直观地表明了无论是方法一、方法二还是文献[5]方法,再进行第二期预测时,其偏差程度明显增大。这说明了灰色模型的可预测长度非常短,进行过长的预测将与实际值产生很大的偏差。
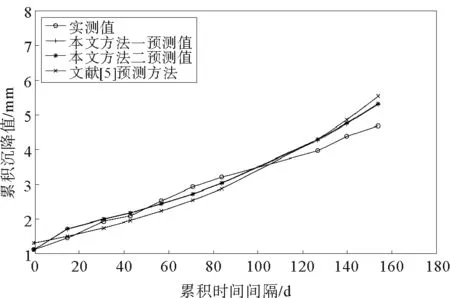
图5 预测值对比图Fig.5 Comparison of predicted values
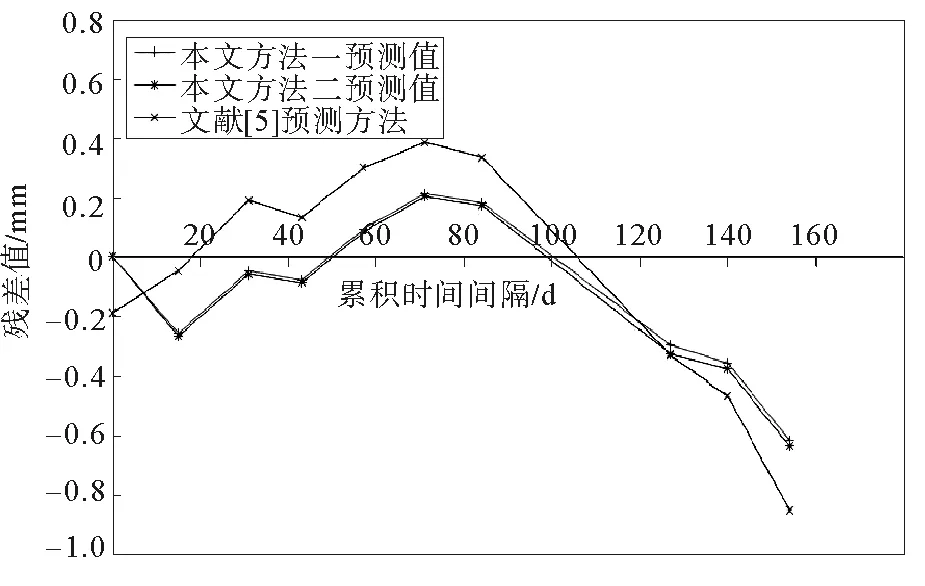
图6 残差值对比图Fig.6 Comparison of residual error
4 结束语
针对非等间距GM(1,1)建模问题,提出了两种基于插值的建模方法:方法一通过插值的方式将非等间距序列构造成等间距序列进行预测;方法二在方法一的基础上运用插值对背景值进行更新构造。因不同的插值方式对不同序列预测的准确程度不一样,提出对非等间距GM(1,1)模型的基于插值的改进需要注重对插值方式的选取。方法一和方法二的不同在于是否采用插值法对背景值进行优化。预测结果显示在对数据进行预测时,方法一比方法二更加准确,原因是多次插值增大了误差。但是当背景值引起的误差大于插值引起的误差时,方法二比方法一更加准确。工程实例证明了两种建模方法可以得到很好的不等间距沉降预测结果,对评判建筑物沉降具有一定参考意义。
参考文献:
[1]DENG J L.Control problems of grey systems[J].Systems & Control Letters,1982,1(5): 288-294.
[2]刘思峰,谢乃明.灰色系统理论及其应用[M].6版.北京:科学出版社,2013:13-14.
[3]党耀国,王正新,钱吴永,等.灰色预测技术方法[M].北京:科学出版社,2015:1-2.
[4]谢乃明,张可.离散灰色预测模型及其应用[M].北京:科学出版社,2016:10-11.
[5]李斌,朱健.非等间隔灰色GM(1,1)模型在沉降数据分析中的应用[J].测绘科学,2007,32(4):52-55.
LI Bin,ZHU Jian.Application of unequal interval grey model in analysis of settlement data[J].Science of Surveying and Mapping,2007,32(4):52-55.
[6]SHEN C G.Grey models for non-equidistant sequence based on trapezoid formula and central difference quotient[J].Journal of Grey System,2010,22(1):17-24.
[7]郑艳琳,刘保东.非等间距GM(1,1)模型的模糊优化[J].山东科技大学学报(自然科学版),2004,23(4):75-77.
ZHENG Yanlin,LIU Baodong.Fuzzy optimization of non-equidistance GM(1,1) model[J].Journal of Shandong University of Science and Technology(Natural Science),2004,23(4):75-77.
[8]尹晖,周晓庆,张晓鸣.非等间距GM(1,1)建模方法对比分析及应用[J].测绘工程,2017,26(2):1-4.
YIN Hui,ZHOU Xiaoqing,ZHANG Xiaoming.Non-equidistant GM(1,1) modeling comparison and application[J].Engineering of Surveying and Mapping,2017,26(2):1-4.
[9]姜峰,郑运虎,梁瑞.改进的非等间距GM(1,1)模型预测腐蚀立管剩余寿命[J].中国安全科学学报,2014,24(6):57-61.
JIANG Feng,ZHENG Yunhu,LIANG Rui.Method for corrosion risers remaining life prediction based on improved non-equidistant GM(1,1) model[J].China Safety Science Journal,2014,24(6):57-61.
[10]李翠凤,戴文战.非等间距GM(1,1)模型背景值构造方法及应用[J].清华大学学报(自然科学版),2007,47(增2):1729-1732.
LI Cuifeng,DAI Wenzhan.Determinator of the background level in the non-equidistant GM(1,1) model[J].Journal of Tsinghua University(Science and Technology),2007,47(S2):1729-1732.
[11]蒋刚,林鲁生,刘祖德,等.边坡变形的灰色预测模型[J].岩土力学,2000,21(3):244-246.
JIANG Gang,LIN Lusheng,LIU Zude,et al.Prediction grey model for slope displacement[J].Rock and Soil Mechanics,2000,21(3):244-246.
[12]姜爱平,张启敏.非等间距近似非齐次指数序列的灰色建模方法及其优化[J].系统工程理论与实践,2014,34(12):3199-3203.
JIANG Aiping,ZHANG Qimin.Methods and optimum of grey modeling for approximation non-homogenous and non-equidistant series[J].Systems Engineering-Theory & Practice,2014,34(12):3199-3203.
[13]沈艳,刘垠,聂龙阳,等.新息累积非等间距GM(1,1)模型研究[J].数学的实践与认识,2016,46(19):228-234.
SHEN Yan,LIU Yin,NIE Longyang,et al.Research of new-information accumulating method for non-equidistant GM(1,1) model[J].Mathematics in Practice and Theory,2016,46(19):228-234.
[14]尹晖,周晓庆,张晓鸣.非等间距多点变形预测模型及其应用[J].测绘学报,2016,45(10):1140-1147.
YIN Hui,ZHOU Xiaoqing,ZHANG Xiaoming.Non-equidistant multi-point deformation prediction model and its application[J].Acta Geodaetica et Cartographica Sinica,2016,45(10):1140-1147.
[15]WANG Q J,WANG C C,XIE A R,et al.An improved SCGM(1,m) model for multi-point deformation analysis[J].Geosciences Journal,2014,18(4):477-484.
[16]GUO X,LIU S F,WU L,et al.A multi-variable grey model with a self-memory component and its application on engineering prediction[J].Engineering Applications of Artificial Intelligence,2015,42(C):82-93.
