基于属性值加权的隐朴素贝叶斯算法

，

(山东科技大学 数学与系统科学学院，山东 青岛 266590)

贝叶斯网络(Bayesian networks, BN)源于概率统计学，作为机器学习的重要方法受到了广泛的关注[1]。在无限制条件下学习最优的BN网络结构是一个NP难问题，所以GREGOR[2]建议在一定的限制条件下寻找最优的BN网络结构，而朴素贝叶斯(Naive Bayes,NB)分类算法是一个很好的解决思路。朴素贝叶斯分类算法是一种以概率密度分析为基础，根据已知事件来预测未知事件发生可能性的分类算法[3]，具有易于实现、计算速度快和分类精确率高的特点，但是当其特征属性条件独立这一假设在一些数据集上被违背时，其分类精确率会降低。因此学者们纷纷通过放松NB算法的假设条件，提出了许多更加优化的改进算法，如树扩展的朴素贝叶斯(tree-augmented Naive Bayes,TAN)算法[4]、平均单一依赖估计(averaged one-dependence estimators, AODE)算法[5]和隐朴素贝叶斯算法[6]等。

其中HNB算法具有分类效率高，计算速度快的特点，且因其给训练集中的每一个特征属性虚构了一个隐藏的父属性，这个隐藏的父属性是由其他所有特征属性共同作用产生的，所以HNB算法极大的放松了朴素贝叶斯分类算法的假设条件，使HNB算法能够在更多的不同种类的数据集上均有较好的分类表现。

但HNB算法提出的构建隐藏父属性的方法太过简单，无法详细地描述训练集中各属性间的相互依赖关系，针对这个问题，许多学者又提出了一些改进的HNB算法。李晶辉[7]提出了双层隐朴素贝叶斯分类(Double-layer Hidden Naive Bayes Classification, DHNBC)算法，该算法在HNB算法的基础上为每个特征属性多引入一个隐藏父属性，表示其他属性与该特征属性相关程度的加权和，其中权值的大小为属性间的条件互信息值。杜婷[8]提出加权隐朴素贝叶斯分类(weighted hidden Naive Bayes classification, WHNBC)算法，该算法利用KL距离和分裂信息的属性权值计算公式来构造相应的加权公式，设计了一个改进的HNB算法。

上述关于HNB的改进算法均是从特征属性出发，而实际上特征属性的不同取值对分类的贡献程度也是不同的[9]。在分类阶段，HNB算法没有考虑测试实例的特征属性不同的取值对分类的贡献程度，这在一定程度上限制了其表现。针对这个问题，本研究提出利用训练集中的相应特征属性值的统计信息来构建加权函数，在分类阶段计算每个测试实例的特征属性在取不同属性值时对分类的贡献程度，并把计算结果作为权重，对HNB算法中用到的条件概率计算公式加权，得到基于属性值加权的隐朴素贝叶斯(attribute value weighting for Hidden Naive Bayes，AVWHNB)算法，然后通过实验验证AVWHNB算法较原始的HNB算法在分类精确率方面有很大的提高。

1 基于属性值加权的隐朴素贝叶斯算法

构建朴素贝叶斯分类器是一个利用给定类标记的训练集构建分类器的过程，其中训练集定义为D={X(1),X(2),…,X(t)}，包含t个训练实例。假设Ai(i=1,2,…,n)是训练集中的n个特征属性，并且假定训练集中有m个类标记，记为C={c1,c2,…,cm}，给定一个具体的测试实例X=(a1,a2,…,an)，这里ai就是特征属性Ai的取值，则可以依据公式(1)来判断测试实例X的类标记。

(1)

HNB算法是结构扩展后的NB改进算法，针对训练集中的每一个特征属性Ai，给其构建一个隐藏的父属性Ahpi，并且Ahpi是由除了特征属性Ai之外的其他所有的特征属性共同作用产生的，ahpi为Ahpi的取值。由此得到HNB算法的分类公式

(2)

本节中将要介绍的AVWHNB算法即是在HNB算法的基础上得到的。

1.1 AVWHNB算法介绍

由公式(2)可以看出，在分类阶段，HNB算法把每个测试实例的特征属性的各个不同取值对分类的贡献看成是一样的，这在一定程度上限制了HNB算法的分类精确度。针对这一问题，构建加权函数wijk对公式(2)中的条件概率计算公式进行加权，得到AVWHNB算法。其中wijk的计算公式如式(3)所示。

(3)

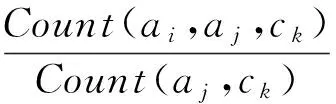
(4)

式(4)中的Wij可由式(5)求得。

(5)

式(5)中的Ip(Ai;AjC)可由式(6)求得。

(6)

公式(6)表示的是训练集中两个特征属性的条件互信息值。

1.2 AVWHNB算法步骤

结合1.1节中的内容，本节给出AVWHNB算法对一个测试实例X=(a1,a2,…,an)的具体分类步骤，如表1所示。

表1 AVWHNB算法步骤Tab.1 Steps of AVWHNB algorithm

在实验时需要计算P(ck)、P(ajck)和P(aiaj,ck)的值。为了避免零概率估计对实验的影响，采用拉普拉斯平滑对上述的概率公式进行估计，其具体的公式[10]为：

(7)

(8)

(9)

在实验前需要对训练集中的数据做如下的预处理：

1) 把训练集中各训练实例的缺失特征属性值补齐，使用的是weka中的无监督过滤器Replace Missing Values；

2) 把训练集中各训练实例的数值型特征属性值离散化，使用的是weka中的无监督过滤器Discretization；

3) 把训练集中无用的特征属性删除，使用的是weka中的无监督过滤器Remove；

4) 把训练集中类标记缺失的训练实例删除，使用的是weka中Instances类下的方法delete with Missing Class。

表1中的第一步为分类器构建过程的训练阶段，第二步和第三步为分类构建过程的分类阶段。第三步中主要是利用公式(4)来判断测试实例X属于哪个类标记，公式(4)得到的结果可以解释为：在设计的公式中，测试实例属于这个类标记的概率最大。

2 实验分析

本节对NB算法、AODE算法、HNB算法和AVWHNB算法进行分类实验，实验采用的数据是UCI标准数据集，数据集的具体描述如表2所示[11]。编程使用Java语言和Weka软件中的core.jar算法包，使用的实验平台为Eclipse，运行程序时的电脑配置为：处理器为AMD Phenom(tm)II P920,内存大小为2 GB。

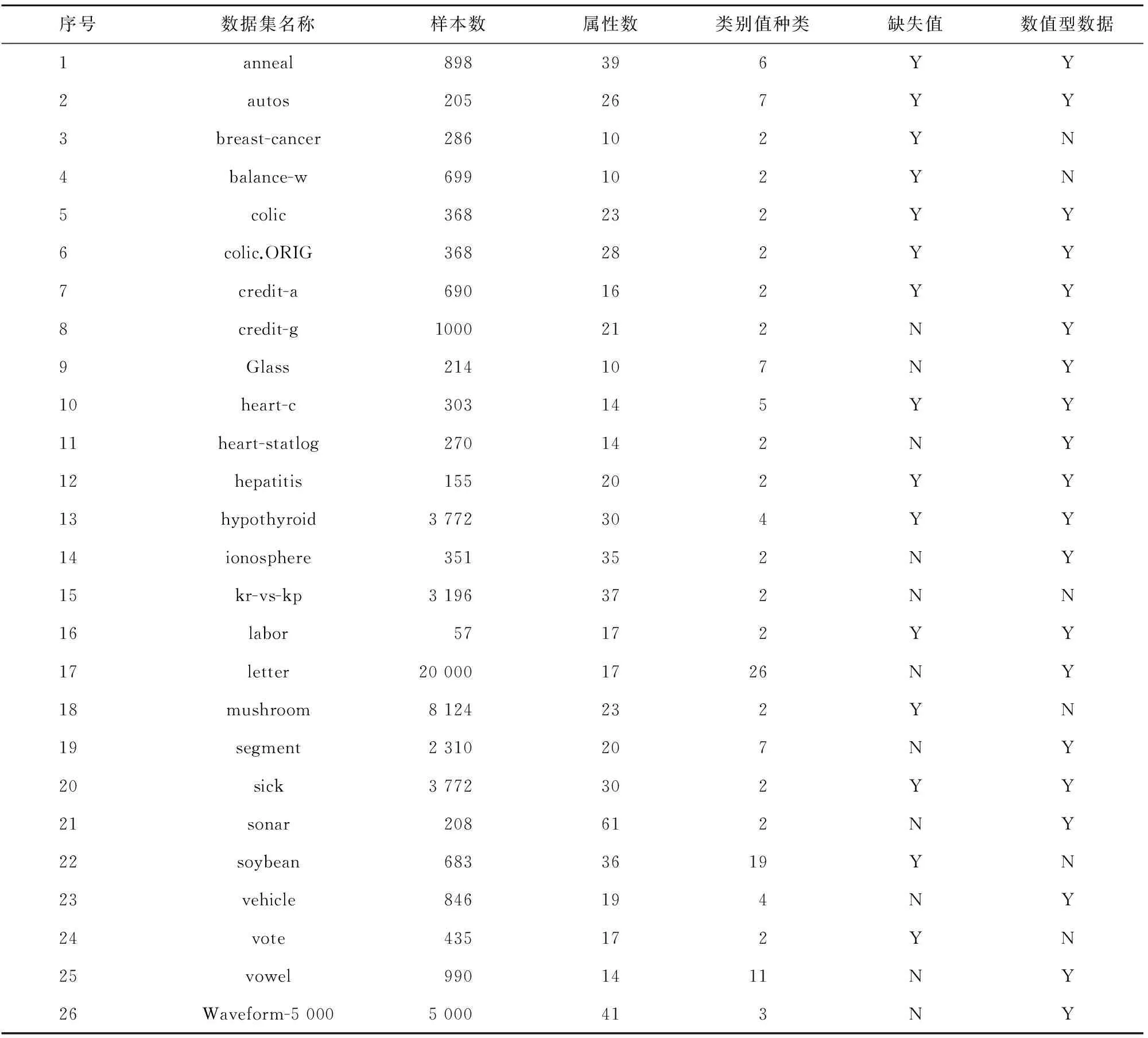
表2 训练集数据描述Tab.2 Training set data description

实验采用的是十折交叉验证的方法。十折交叉验证指的是将一个原始训练数据集平分成10份，进行10次实验，每一次都是将这10份数据中的1份作测试集、9份做训练集，10次实验结果的平均值为最终的结果[12]。在上面的准备工作后，通过数值实验得到了NB、AODE、HNB和AVWHNB算法的分类精确率，如表3所示。

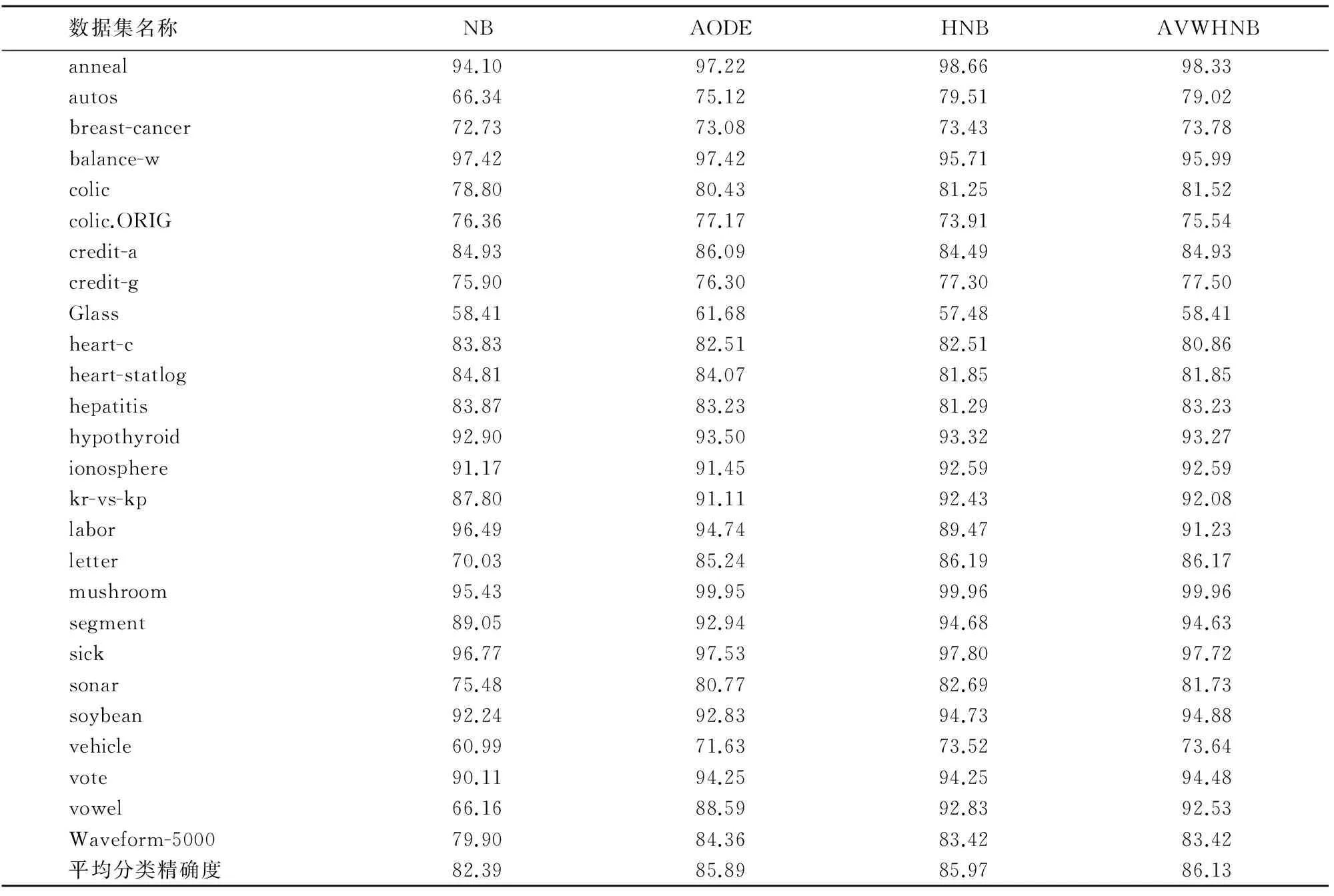
表3 各算法分类精确率对比Tab.3 Classification accuracy comparison of different algorithms %

对比这4个算法在每一个训练集上的表现得到表4。

表4 各算法在每个数据集上的分类精确率对比Tab.4 Classification accuracy comparison of different algorithms at each dataset

对比上述4个算法的时间复杂度得到表5。

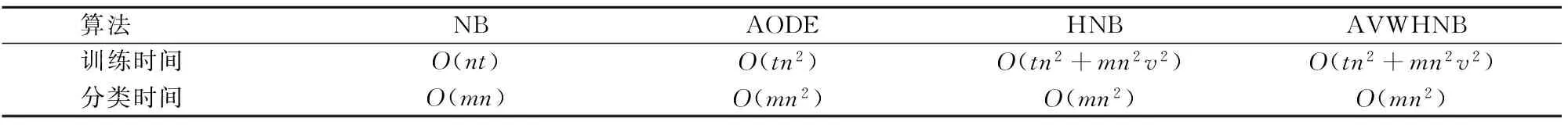
表5 各算法时间复杂度对比Tab.5 Time complexity comparison of different algorithms

在表5中，m是类标记的种类数，n是特征属性的数目，v是一个特征属性的各个属性值的平均数目，t是训练集中训练实例的数目[13]。

由表3可知AVWHNB算法的平均分类精确率大于NB算法、AODE算法和HNB算法。由表4看出AVWHNB算法分类效果好的数据集数目多于NB、AODE和HNB算法。由表5可以看出AVWHNB算法的训练时间、分类时间和HNB算法相同，即AVWHNB算法的时间复杂度和HNB算法相同。综合上面的分析可知，AVWHNB算法在提高分类精确率的同时并未增加算法的时间复杂度，这充分说明了AVWHNB算法的分类效果比HNB算法好。

从表3和表4的数据中可以看出AVWHNB算法也存在着一些不足。首先，当数据集中各特征属性间的关联程度较弱[14]时，其在某些数据集上的表现不如NB算法。其次，在某些数据集上的表现不如原始HNB算法说明AVWHNB算法的稳定性有待提高。针对上述问题，在分类中常用的多分类器思想是一个很好的解决办法，而针对于多个分类器的输出，则可以用投票机制来进行综合以给出最终的分类结果[15-16]。

4 结束语

本研究提出的AVWHNB算法为一种改进的HNB算法，其核心思想是利用构建的加权函数计算各个特征属性值对分类的贡献程度，并将得到的结果对HNB算法中用到的条件概率计算公式加权来改进HNB算法，然后通过实验对比了AVWHNB、HNB、NB和AODE算法的平均分类精确率、在每个数据集上的分类精确率和时间复杂度，结果显示AVWHNB算法的整体分类效果要优于原始的HNB算法。

虽然AVWHNB算法的整体分类效果要优于HNB算法，但在对比每个数据集上的分类效果时，AVWHNB算法分类效果好的数据集的数目只是略高于HNB算法，这说明改进的算法还是不够稳定，所以在以后的研究中，可以将特征属性值加权和特征属性加权相结合，并借鉴AODE算法聚合分类器的思想。具体的思路是：先找到一个合适的方法来判断数据集中各个特征属性的关联程度。然后设置一个阈值，当关联程度低于这个阈值时可以使用NB算法来对数据集进行分类，而当关联程度高于这个阈值时可以采用AVWHNB算法对数据集进行分类。对于这两类分类器，在每一类上均可以设置多个分类器，在具体分类时可采用某种方法将原始数据集分成若干份，每一份数据都由一个分类器来处理。最后用投票机制综合多个分类器的分类结果来确定测试实例的类标记。经过上述处理，理论上可以得到分类效果好且稳定的HNB改进算法。

参考文献：

[1]秦锋，任诗流，程泽凯，等.基于属性加权的朴素贝叶斯分类算法[J].计算机工程与应用，2008,44(6):107-109.

QIN Feng,REN Shiliu,CHENG Zekai,et al.Attribute weighted Naive Bayes classification[J].Computer Engineering and Applications,2008,44(6):107-109.

[2]GREGORY F C.The computational complexity of probabilistic inference using Bayesian belief networks[J].Artificial Intelligence,1990,42(2/3):393-405.

[3]王辉，黄自威，刘淑芬.新型加权粗糙朴素贝叶斯算法及其应用研究[J].计算机应用研究，2015,32(12):3668-3672.

WANG Hui,HUANG Ziwei,LIU Shufen.Novel weighted rough naive Bayes algorithm and its application[J].Application Research of Computers,2015,32(12):3668-3672.

[4]FRIEDMAN N,GEIGER D,GOLDSZMIDT M.Bayesian network classifiers[J].Machine Learning,1997,29:131-163.

[5]GEOFFREY I W,JANICE R B,WANG Z H.Not so Naive Bayes:Aggregating one-dependence estimators[J].Machine Learning,2005,58(1):5-24.

[6]JIANG L X,ZHANG H,CAI Z H.A novel Bayes Model:Hidden Naive Bayes[J].IEEE Transactions on Knowledge and Data Engineering,2009,21(10):1361-1371.

[7]李晶辉.基于互信息的多层隐朴素贝叶斯算法研究[D].长沙:湖南大学,2012.

[8]杜婷.基于属性选择的朴素贝叶斯分类[D].合肥:中国科学技术大学，2016.

[9]CHANG H L.A gradient approach for value weighted classification learning in Naive Bayes[J].Knowledge -Based Systems,2015,85:71-79.

[10]ZHONG L X,XIANG R Y,DAE K K.Experimental analysis of Naive Bayes classifier based on an attribute weighting framework with smooth kernel density estimations[J].Applied Intelligence,2016,44(3):611-620.

[11]MERZ C,MURPHY P,AHA D.UCI repository of machine learning database[DB/OL].[2017-09-08],http://www.ics.uci.edu/mlearn/MLRpository.html.

[12]袁梅宇.数据挖掘与机器学习WEKA应用技术与实践[M].北京：清华大学出版社，2014:330-333.

[13]ZHONG L X,DAE K K.Attribute weighting for averaged one-dependence estimators[J].Applied Intelligence,2017,46(3):616-629.

[14]JUN Y.Correlation coefficient between dynamic single valued neutrosophic multisets and its multiple attribute decision-making method[J].Information,2017,8(2):41.

[15]CAGATAY C,MEHMET N.A sentiment classification model based on multiple classifiers[J].Applied Soft Computing,2017,50:135-141.

[16]ANDRONIKI T,GEORGE E T,ANASTASIOS R,et al.A methodology to carry out voting classification tasks using a particle swarm optimization-based neuro-fuzzy competitive learning network[J].Evolving Systems,2017,8(1):49-69.