新型城镇化与居民消费关系的实证分析

范兆媛，周少甫

（1.南京邮电大学 经济学院，南京 210023；2.华中科技大学 经济学院，武汉 430074）

0 引言

我国经济发展的潜力与动力来自城镇化。但过去我国城镇化“摊大饼”、粗放式的发展模式，对生态环境和居民身体健康造成了很大影响，国家适时提出了更加注重质量的城镇化发展思路。因此，研究新型城镇化的发展与居民消费率两者之间的关系具有现实意义。

空间面板模型包括静态空间面板模型和动态空间面板模型两大类。动态模型更系统地考虑了“时间-空间”的综合交互作用，因此在实证研究中得到了更为广泛的应用。动态空间面板模型主要分为两类，一类是因变量的滞后项以及空间交互效应项都出现在模型中[1-3]；另一类是空间交互项仅出现在扰动项中的模型[4,5]。大部分对动态空间面板模型的研究都考虑了(N，T)都很大的情形。但是，在微观经济学和有关产业组织的实证分析中，情况则有所不同，T有可能比较小。因此，本文在Sarafidis[4]的基础上，研究了时间跨度比较小的情况下的空间动态误差面板模型。本文通过短面板空间动态误差模型，构建新型城镇化综合评价指标，充分考虑城镇化对居民消费影响的“时间-空间”关联，研究了新型城镇化对居民消费水平的影响。

1 研究设计

1.1 新型城镇化综合指标（URBAN）

城镇化率通常使用城市中常住人口的数量跟总人口的比值来衡量，但是在城市中工作和生活的农民工也算作常住人口，他们虽然用来计算城镇化率，但是却没有跟有城市户籍的人口享受到同样的福利待遇，这样计算的城镇化是不完全的。因此，本文在新型城镇化内涵的基础上，利用熵权法选取26个变量建立新的衡量新型城镇化的评价指标体系（见表1），具体步骤如下：

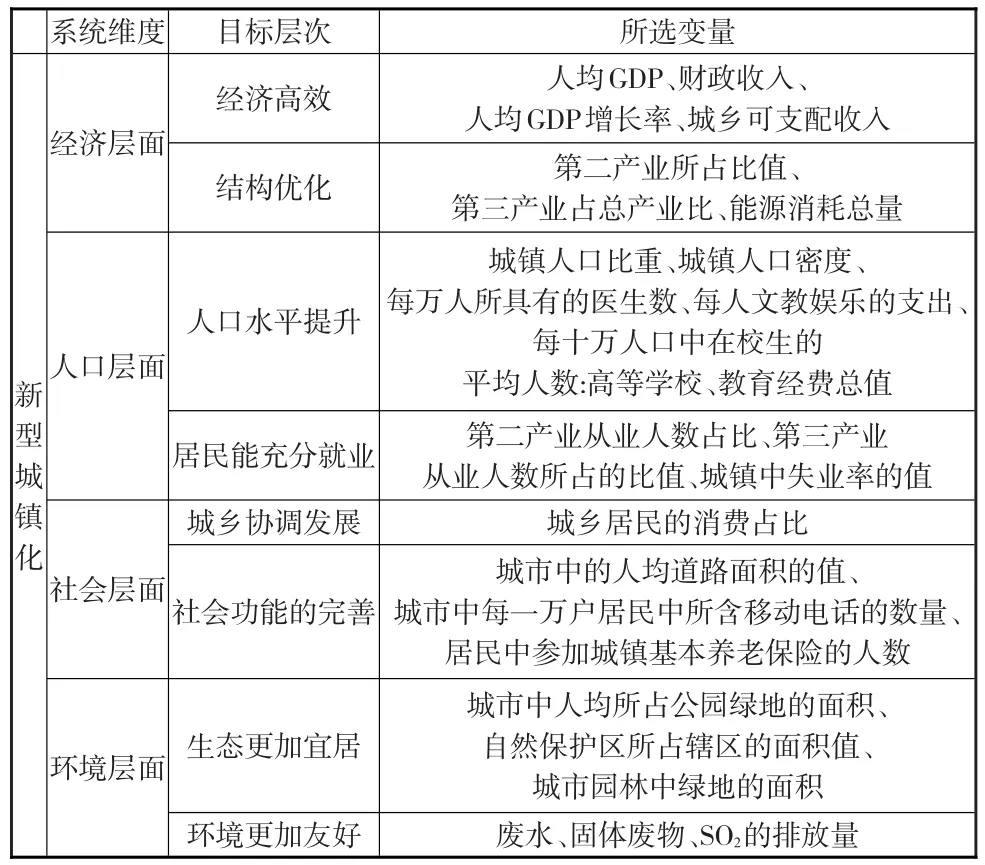
表1 新型城镇化指标

第一步：无量纲化处理，其中式（1）中的Xij衡量第i个省份，第j（j取自于所选的26个变量）个变量对应的新型城镇化评价指标的值：

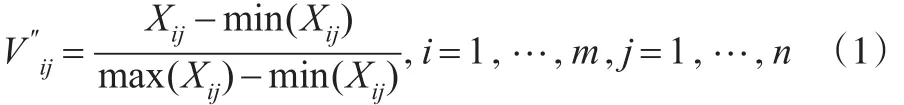
第三步：计算熵值E跟差异系数F：

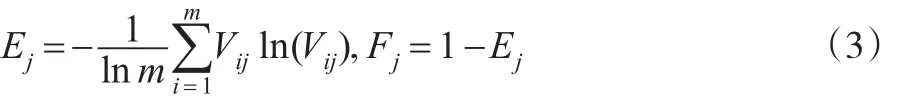
第四步：第j个指标占总指标的比值为：

第五步：确定新型城镇化的综合指标值：

表2给出了2004—2015年30个省域的新型城镇化指标值跟该值在30个省域的排名，为了方便比较，指标值做了扩大10倍处理。由表2得出，新型城镇化排名的前三名是广东、江苏与山东，可以看出建立的综合评价指标值跟中国的经济发展水平是相关的。

表2 2004—2015年新型城镇化指标与排名

1.2 数据来源

除了城镇化以外的指标的衡量：居民的消费水平通过居民消费支出跟GDP的比值进行计算；为了更好地估计消费水平的影响，加入了可能影响消费的一些因素，其中城乡收入差距（GAP）是用城镇居民获得的可支配收入与农民纯收入之比来衡量；老年抚养比（ODR）的值通过年龄不低于65岁的老人人口数量与15～64岁的人口数量的比值进行衡量；利用CPI来衡量通货膨胀率。因为西藏数据不全，本文选取2004—2015年中国30个（不包含西藏）省域的数据，通过wind数据库、统计年鉴获得研究所用的数据。

1.3 模型设定

选取空间动态误差模型进行研究，具体模型如下：

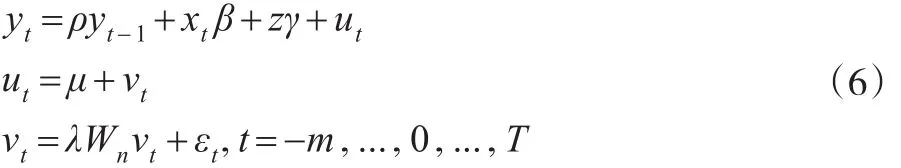
其中，yt代表居民消费率，yt-1代表消费率的滞后一期的值，xt是自变量，代表新型城镇化、老龄化、通货膨胀率以及城乡收入差距的值，z衡量截距项的值，Wn是地理空间距离权重矩阵，其中d为区域i的地理位置中心到区域 j的地理中心的距离。

为了检验结论的一致性，引入空间误差模型（SEM），设定如下：

1.4 计量模型的估计

运用一阶差分消除固定效应：

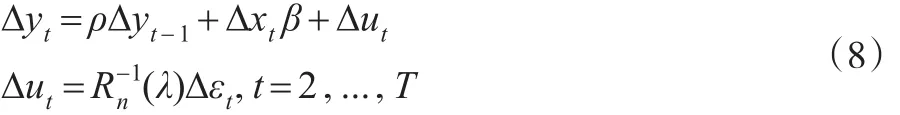
注意到式（8）在t=1处是没有定义的，因为Δy1依赖于Δy0的取值，而Δy0是无法观测的。Su和Yang（2015）[13]把 Δy1分解为内生部分和外生部分，利用ΔxT)′作为Δy1中内生部分的最优预测变量。利用式（9）来构建相应的似然函数：

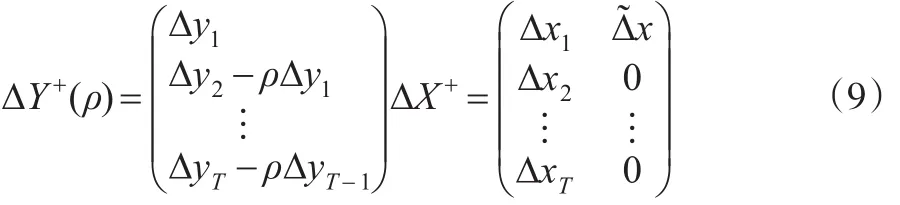
Su和Yang（2015）[5]给出的基于 Δy1的QMLE方法。由于已经得到了关于的QMLE估计，则基于如下的水平值方程：

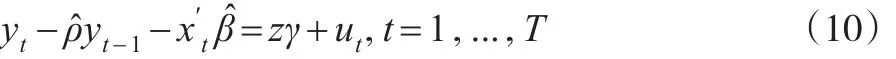
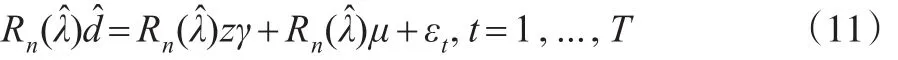
那么基于式（11），就得到了关于γ估计的表达式：

2 实证分析

2.1 消费水平的探索性空间分析

居民消费的Moran’s I检验结果如表3所示。

表3 居民消费的Moran’s I检验结果

从表3的结果得出，除了2015年，莫兰指数I（Moran’s I），其他年份的值都是显著（10%的水平）为正的，这表明居民消费率在空间上存在相关性。

2.2 空间动态误差模型的结果分析

在进行QMLE估计之前，首先要确定起始期m的值。由于城镇化被官方首次采用是在2000年，因此本文选取m的值为5。表4给出了QMLE的估计结果。

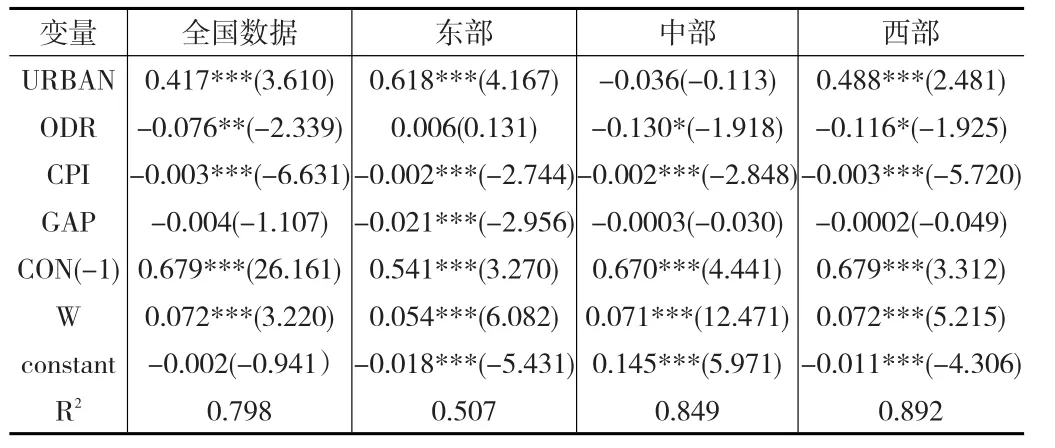
表4 短面板动态SEM模型回归结果

从表4的全国数据中可以得出，R2的值为0.798，表明模型拟合较好。滞后一期居民消费率对当期消费率存在显著的正影响，影响大小为0.68，与1相比仍然较小，说明QMLE方法是可信的。新型城镇化水平的提高对消费水平的提高有显著的促进作用，这充分表明提高我国新型城镇化水平的必要性，要努力打破城乡二元经济结构；随着户籍制度的消除，进一步推进我国的城镇化。老龄化对消费率存在显著的负的影响，这也说明了国家推出二胎政策的必要性，促使人口年龄结构的优化，同时也要致力于提高老年人的社会保障水平。通货膨胀率对消费水平存在显著的负的影响，这说明政府需要控制通货膨胀率在合理的范围内，保证物价稳定。城乡收入差距对消费水平的影响不显著。扰动项中空间关联项的系数估计值是显著的，表明存在显著的空间效应，选用空间模型是合适的。

对于分区域的回归结果可以得出：新型城镇化对东部和西部的影响是显著的正的影响，且对东部地区的影响值达到了0.618，但是对中部地区的影响不显著，这表明应该更多地关注中部地区的城镇化水平，东部地区的新型城镇化的改变对消费率的影响相对西部区域较弱，需要努力提升西部的城镇化水平，改善中部城镇化水平不合理的因素；老龄化对中部和西部都存在显著的负的影响，但是对东部的影响不显著，这可能与东部地区较高的城镇化水平有关，年轻人更多的流入到东部相对发达的地区，中部和西部相对落后，老龄化比较严重，应该更多地关注中部与西部地区的发展，为更多的年轻人创造就业机会，响应国家二胎政策的号召等方式减少老龄化水平，进而提高消费水平；通货膨胀水平的提高显著地抑制了东部、中部以及西部地区的消费水平，应该维持CPI的值在合理的范围内；对东部地区,城乡收入差距的消费水平存在显著的负的影响，收入差距在一定程度上减少了居民的消费率，但是城乡收入差距对西部和中部地区的影响不显著，因此需要进一步地减少东部地区的收入差距水平；对东部、中部以及西部，消费率的滞后一期的值对消费率的当期值存在显著的正的影响，影响值在0.541～0.679之间，这说明居民的消费相对比较稳定。

2.3 稳健性检验

为了检验模型的相对稳定性，表5给出了利用空间误差模型回归的结果。新型城镇化（URBAN）、老年抚养比（ODR）、CPI对全国及东、中、西部居民消费水平的影响与表5是一致的，且空间误差项的系数显著的异于0，存在空间效应；城乡居民差距（GAP）对消费水平的影响与表5的结果存在一定的差异，对全国数据以及中、西部地区，城乡收入差距（GAP）的增加提高了居民消费率的值，这与表5中的结果存在差异，但新型城镇化（URBAN）、老年抚养比（ODR）、CPI对消费率的影响是一致的，利用空间动态面板模型研究新型城镇化对居民消费影响的结论是稳健的。

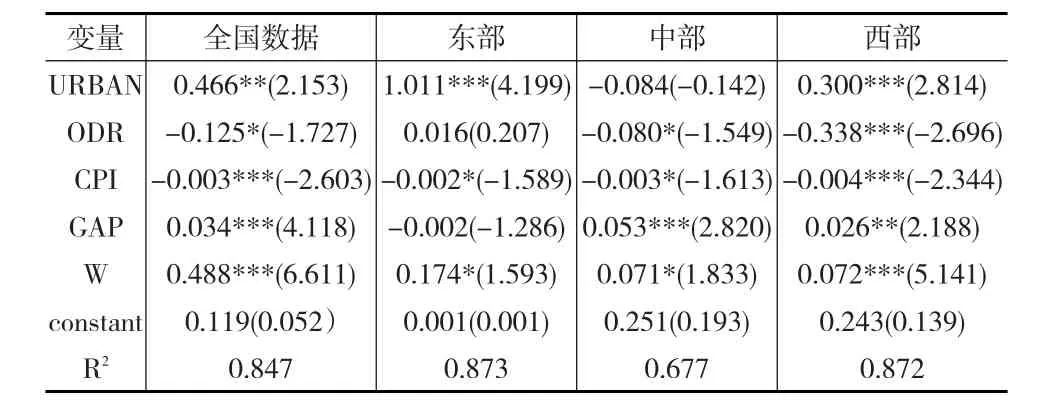
表5 SEM模型估计结果

3 结论

本文通过构建新型城镇化的指标，基于2004—2015年的30个省域数据，利用短动态面板空间误差模型的QMLE估计方法研究了新型城镇化对居民消费率的影响。结论如下：

（1）对总体数据：新型城镇化水平的提高对消费水平的提高有显著的促进作用；通货膨胀率对消费水平存在显著的负影响；老龄化（ODR）对居民消费率的影响是显著的负值；扰动项中空间关联项的系数估计值是显著的，表明存在显著的空间效应，选用空间模型是合适的。

（2）分区域而言：新型城镇化对东部以及西部的影响是显著的正的影响，且对东部地区的影响值更大，但是对中部地区的影响不显著，这表明应该更多地关注中部地区的城镇化水平；老龄化（ODR）对中部及西部都存在显著的负的影响，但是对东部的影响不显著，中部以及西部相对落后，老龄化程度比较严重，应该更多地关注中部与西部地区的发展；通货膨胀水平的提高显著地抑制了东部、中部以及西部地区的消费水平，应该维持CPI的值在合理的范围内；对东部地区而言，城乡收入差距的消费水平存在显著的负的影响，但是城乡收入差距对西部和中部地区的影响不显著；对东部、中部以及西部，消费率的滞后一期的值对消费率的当期值存在显著的正的影响，影响值在0.541～0.679之间，这说明居民的消费相对比较稳定。

参考文献:

[1]Yu J H,Jong De,Lee R,Quasi-Maximum Likelihood Estimators for Spatial Dynamic Panel Data With Fixed Effects When Both N and T Are Large[J].Journal of Econometrics,2008,146(1).

[2]Lee L F,Yu J H.A Spatial Dynamic Panel Data Model With Both Time and Individual Fixed Effects[J].Econometric Theory,2010,26(2).

[3]Yu J,Jong R D,Lee L F.Estimation for Spatial Dynamic Panel Data With Fixed Effects:The Case of Spatial Cointegration[J],Journal of Econometrics,2012,167(1).

[4]Vasilis S.GMM Estimation of Short Dynamic Panel Data Models With Error Cross-Sectional Dependence[C].MPRA Paper,University Library of Munich,Germany,2011.

[5]Su L J,Yang Z L,QML Estimation of Dynamic Panel Data Models With Spatial Errors[J].Journal of Econometrics,2015,185(1).