基于改进人工鱼群算法的模糊时间序列模型

鲜思东，张建锋

（重庆邮电大学a.复杂系统智能分析与决策重点实验室；b.自动化学院,重庆 400065）

0 引言

在过去几十年中，人们提出了许多预测模型来处理各种领域中的预测问题，其中时间序列模型是人们最常用到的预测模型之一，当历史数据为语言值等不确定信息时，经典时间序列模型就无法对历史数据进行有效的预测。1965年，Zadeh[1]首次提出模糊集理论,为处理模糊数据提供了理论依据。Song等[2-4]将模糊集理论融入时间序列建模过程,给出了模糊时间序列预测模型(FTS)。在模糊时间序列的研究初期对论域大多采用均等划分[2，3]，随着研究的不断深入,人们打破等区间划分限制,给出了一些非等分的论域划分方法,如基于蚁群算法(GA)[5]、粒子群优化算法(PSO)[6-8]的论域划分方法、基于比例论域划分方法[9]、基于模糊c均值聚类算法的论域划分方法[10]和其他非等分论域划分方法[11，12]。模糊关系的构建对模糊时间序列的预测具有重要的影响，Song[2-4]先定义一个“乘”运算，用预算结果得到的矩阵表示模糊关系,而Chen[13]提出一种新的构建模糊逻辑关系矩阵的方法,Aladag[14]提出使用人工神经网络来确定模糊逻辑关系。

大量的研究表明，模糊论域区间的划分方式和模糊逻辑关系的构建方法是影响模糊时间序列模型预测精度最重要的两个方面。为此,本文通过改进人工鱼群算法，给出一种新的模糊时间序列论域区间的划分方法，提出一种基于改进人工鱼群算法的模糊时间序列预测模型。新模型使用Chen[15]提出的模糊关系表和模糊逻辑组关系表来确定模糊关系。为了获得较好的预测值，新模型在训练数据集和测试数据集两个阶段分别采用Kuo[7]提出的EBN(estimating based on next state）和 MV(master voting）这两种方法进行预测分析。通过对美国Aalbama大学[2]的注册人数进行预测，实验结果表明了所提出算法的有效性。

1 模糊时间序列

其中，fAi(⋅)为模糊集合 Ai的隶属函数,fAi(⋅):U→[0，1]:fA(ui)为ui在模糊集A上的模糊隶属度函数值,并且 fA(ui)∈[0，1]，1≤i≤n[1]。

定义1：令R中一个子集Y(t)(i=1，2，…)为给定论域,fi(t)(i=1,2,…)为定义在其上的模糊集合，且 F(t)={f1(t)，f2(t)，…},则称 F(t)为定义在Y(t)上的模糊时间序列[2]。

定义2：假设F(t)由 F(t-1)确定，即F（t-1→F(t)），可以表示为 F(t)=F(t-1)◦R(t-1，t),称作 F(t)的一阶模糊时间序列模型,R(t-1，t)为F(t)与F(t-1)之间的模糊关系[2]。

定义 3：F(t-1)=Ai，F(t)=Aj，则称 Ai→Aj为一个模糊逻辑关系（可简称为模糊关系）,其中Ai称为模糊关系的前件,Aj称为模糊关系的后件[2]（若有模糊关系重复出现,则只保留一组）。

定义4：若模糊时间序列F（t）存在一组模糊逻辑关系

设U为论域,将U划分为 n个子区间,即U={u1，u2，…，un},则定义在论域U中的模糊集合A可表示为：，则模糊逻辑关系组可以简记为

2 改进的全局人工鱼群算法（IGAFS）

人工鱼群算法[16]模拟鱼群的群体行为进行随机寻优的搜索，主要包含人工鱼的觅食、聚集、追尾等行为,利用局部最优信息逐步迭代，达到全局寻优的目的。

一条人工鱼代表空间中一个点，可以表示为X=(x1，x2，…xn),其中 xi(i=1，2，…n)为欲寻优的变量；人工鱼个体所在位置的适应度为Y=f(X)，本文的Alabama大学注册人数的预测致力于Y最小化;鱼群规模 fishnum,两条人工鱼之间的距离计算公式为，人工鱼移动（迭代）的最大步长用step表示；人工鱼群的拥挤因子用δ表示;人工鱼的感知范围用νisual表示；移动（迭代）次数用try_number表示，r为区间(0,1)内的随机数。

（1）聚群行为

聚群行为是人工鱼个体在移动程中自然地聚集成群向邻域中心移动的行为。设人工鱼当前位置状态为Xi,探寻其邻域内(即dij＜νisual)伙伴数目nf及中心位置Xcenter，计算该聚群中心的适应度（即食物浓度）。在求极小值问题中，如果Ycenter*nf＜δ*Yi,表明中心位置 Xcenter处有较多食物且伙伴数量不太多,则该人工鱼向中心位置Xcenter前进一步。其计算公式为：

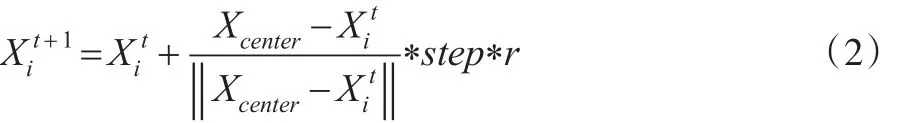
否则，继续执行觅食行为。

（2）追尾行为

追尾行为是一种人工鱼向着附近有着最优适应度移动的行为。设人工鱼当前状态为Xi,搜索当前邻域内（即dij＜νisual）的伙伴中适应度值最小的伙伴Xmin,此时其对应的适应度值为Ymin。在求极小值问题中,如果Ymin*nf＜δ*Yi,表明在Xmin处具有较高的食物浓度并且其伙伴数量不太多,那么朝Xmin前进一步。其计算公式为：

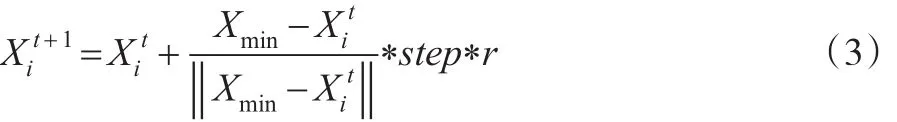
否则，继续执行觅食行为。

（3）觅食行为

觅食行为是人工鱼根据食物浓度趋向较优适应度的基本行为。设人工鱼当前位置状态为Xi,在其感知邻近范围内随机选择一个状态Xj：

式中,Rand()是一个介于-1和1之间的随机数,在求解极值问题中,若Yi＞Yj,则向该位置前进移动一步：

反之,在邻近范围内重新随机选择状态Xj,判断是否满足前进迭代的条件,反复尝试try_number次后，如果仍不满足前进移动条件,则执行下一步的随机行为。

（4）随机行为

随机行为就是在人工鱼的视野中随机选择一个位置状态,然后向该方向移动，其他它是觅食行为的一个缺省行为。计算公式为：

其中，Rand()是一个介于-1和1之间的随机数。

另外，人工鱼群算法通过设置公告牌来记录最优状态和当前迭代的最优人工鱼位置信息。

为了提高人工鱼群算法的全局搜索能力,克服传统人工鱼群算法计算精度低、后期收敛速度慢、复杂度较高等缺点,江铭炎和袁东风[17]在人工鱼的位置更新公式中加入全局最优信息,提出了全局人工鱼群算法(GAFS)。但是该GAFS中各人工鱼在随机行为阶段只能在其视野范围内产生随机状态,这就使得各条人工鱼的搜索范围太小,不利于算法跳出局部最优。

为了扩大每条人工鱼的搜索范围。本文在随机行为阶段,将随机状态的选择范围扩大到整个鱼群搜索区域,从而增强了全局人工鱼群算法跳出局部最优解的能力。AFS算法中鱼的聚群、追尾、觅食和随机行为的公式（2）、公式（3）、公式（5）和公式（6）修改为如下新的公式：

其中，Xbest为全局最优位置,xmin为人工鱼搜索范围的最小边界值,xmax为人工鱼搜索范围的最大边界值。

3IGAFS-FTS预测模型

模糊区间是模糊时间序列模型建立的基石,模糊区间划分是决定模糊时间序列预测精度的关键因素,为了能够更好地提高预测精度,更加真实地反映数据的内部结构,本文将IGAFS算法用于模糊区间的划分中,建立了IGAFS-FTS预测模型,具体实现步骤如下:

步骤1：设置数据集和初始化参数

将数据集中的数据分为训练集和测试集。设置FTS中模糊区间的个数n和模型阶数λ,初始化IGAFS算法相关参数,包括各人工鱼所含参数数目d=n-1、人工鱼的群体规模 fishnum、最大迭代次数MAXGEN等。

步骤2：定义论域

步骤3：初始化人工鱼的位置并计算其对应的适应度值

在人工鱼群算法中,每条人工鱼的位置由d维参数向量 Xid=(xi，1，xi，2，…，xi，d) 来表示,Xid表示论域 U 的一组分隔点。每条人工鱼都从论域U内随机产生d个数据,并将这d个数据按从小到大的顺序排列,作为各条人工鱼所对应的初始化位置向量,计算此时各条人工鱼（即可能解）所对应的适应度值 fitness,适应度值的计算过程如下所示:

步骤3.1：数据模糊化

根据每个人工鱼所对应的位置向量来划分论域U,运用文献[13]中定义的论域及模糊集的方法将数据模糊化,给出相应的模糊时间序列。

步骤3.2：建立模糊逻辑关系和模糊逻辑关系组

经上文的分析可知,不同的论域划分所得到的模糊时间序列是不同的,进而所构成的模糊逻辑关系组也是不同的。根据上一步所确立的各组模糊时间序列数据和预先给定的模糊时间序列的模型阶数,确立相应的模糊关系和模糊关系组表。例如,假设某个具有23个观测值的时间序列,在某种论域划分下，得到表1所示的模糊时间序列,表2给出其所对应的模糊关系组。

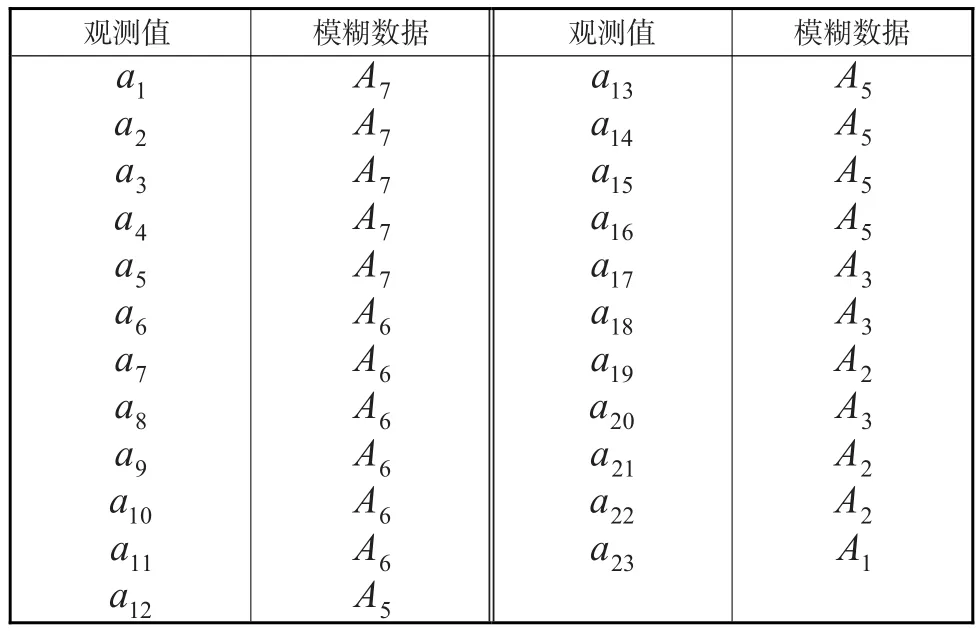
表1 样本模糊时间序列

表2 样本模糊时间序列的模糊逻辑关系组

步骤3.3：去模糊化及求预测值

通过对上面得到的各模糊逻辑关系组进行解模糊运算,进而得到在不同论域划分下所对应的预测值。训练与测试数据集分别采用EBN和MV这两种方法来获得预测值。

在EBN预测方法中:将各个模糊逻辑关系组中,所含的每条模糊逻辑关系右件模糊值(Ai)所对应的区间均分为3块,然后通过公式（11）计算得到预测结果：

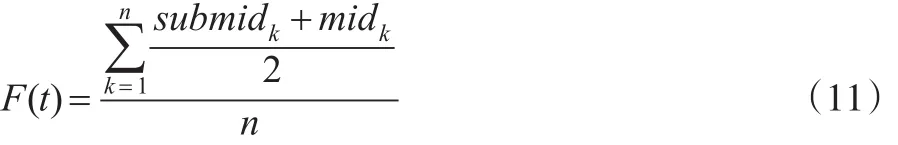
其中，F(t)为预测值,n为同一个模糊逻辑关系组中所含的不同模糊逻辑关系的个数;midk(1≤k≤n)为模糊逻辑关系右件模糊值Ak所对应区间的中点值;submidk为将模糊逻辑关系右件模糊值Ak所对应区间均分为3个区间后,其中某个区间的中点值。例如:表2中所给出的第2个模糊逻辑关系组,它只有一个右件模糊值A6。此时,本文的目标是预测表1中所给出的第6个观测值,假设这个观测值的实际值是76100,A6所对应的模糊区间为 I6=(75000，76500],将其均分为3个子区间，此时,其所对应的3个子区间为。根据上面这些信息,按照EBN预测方法,可知区间 I6的中点值为mid6=75750,实数。因此,得到对应的模糊关系为F(t-2=在子区间 SR6.3中,此时76500)/2=76250,进而,可以得到的预测值为：

本文采用等Kuo等[6]提出的MV预测方法来获得测试数据集的预测值,原文献在建立模糊关系时使用前λ年的数据来做预测,通过MV预测方法来计算测试数据集的预测值,预测值计算公式如下：

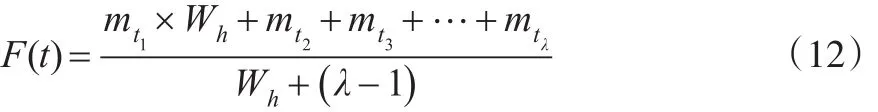
其中，F(t)为第t年的预测值,λ表示预测用到几年的数据,Wh表示前一年的数据对预测下年数据的影响程度,表示之前第i年模糊数据集区间的中点值,不同的Wh值不同的对应预测精度,选取实验过程中使得精度最好的Wh。

步骤3.4：计算适应度值

本文采用预测值与实际值的均方误差(MSE)函数来评价算法的预测性能,MSE公式如下：

其中，Xforecasted（t） 和 Xactual（t）分别为t时刻样本数据的预测值和实际值,N是预测值的个数。

在初始化人工鱼群阶段,比较初始化鱼群中各人工鱼所对应的适应度值,将最小适应度值所对应的位置向量赋给Xbest。用公告牌来记录最优状态和当前迭代的最优人工鱼位置信息。

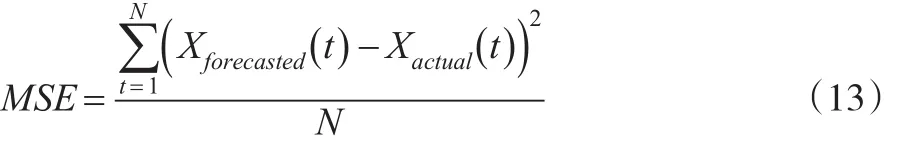
步骤4：人工鱼行为选择

每条人工鱼分别执行IGAFS中的觅食、聚群、追尾和随机行为等步骤,不断更新人工鱼个体的位置状态信息,寻找并保存全局最优值,将最优人工鱼位置向量赋给Xbest。

步骤5：行为终止判断

对是否达到鱼群的最大迭代次数进行判断,若未达到最大迭代次数，则迭代次数加1,跳转至步骤3继续执行;若已达到最大迭代次数，则输出鱼群的最优适应度值和最优值对应的人工鱼位置向量。

4 应用实例

为了验证所提出算法的有效性,本文选取表3中给出的一组Alabama大学1971—1992年的注册人数[2]作为样本数据进行比较研究。

表3 实际注册人数、模糊化数据

4.1 训练数据集的应用结果

步骤1：数据集设置和参数初始化

模糊区间的个数为n=7,各人工鱼所含参数数目为d=6,模型阶数λ=2,人工鱼的群体规模 fishnum=100,最大迭代次数MAXGEN=150,人工鱼的感知距离νisual=500,拥挤因子delta=5,最大移动步长step=600*rand（rand为[0,1]内的随机数）,最大试探次数try_number=30。

步骤2：定义论域

步骤3：初始化人工鱼的位置并计算其对应的适应度值

通过步骤3.1至步骤3.4得到初始化人工鱼群的位置向量,并将最小适应度对应的位置向量赋给Xbest。

步骤4：用IGAFS得到全局最优适应度值

每条人工鱼分别执行IGAFS的觅食、聚群、追尾和随机行为4个步骤，不断更新人工鱼个体的位置状态信息,然后保存全局最优位置向量值，经过150迭代后，得到使MSE结果最优的全局最优参数向量为：

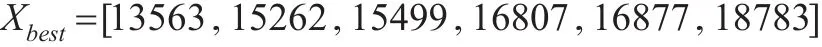
此时，所对应的MSE=48875,结果如表3所示。

在表4中,将本文提出的预测方法与HPSO（使用2阶模糊时间序列）[6],Cheng[12]，CCO6H[18],Egioglu[19]和Chen[20]等模型的预测结果进行比较,结果表明在训练数据集阶段新方法优于其他模型。

表4 不同方法预测结果比较

4.2 测试数据集的应用结果

为了确定所提出方法预测未来数据的能力，将数据集中最后的3个观测值作为测试数据集，并对这3个观测值进行预测。为剩下的19个观测值创建相应的模糊关系,预测得到对应测试集中的数据,通过预测值与实际值的均方误差(MSE)来评估预测未来数据的能力。

本文测试集的分析与其他方法一样，都是通过MV预测方法，得到测试集中的数据。通过大量研究发现2阶模型时可以获得最好的预测精度。

表5给出在相同的区间数目n=7、模型阶数λ=2和Wh=15下,HPSO[6]，AFPSO[21]和本文提出的新方法在测试阶段的预测精度。

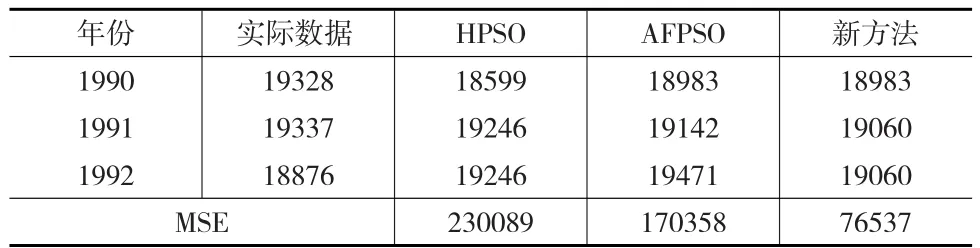
表5 不同方法预测结果比较

由表5可以看出本文所提出的方法MSE最小，这表明对于Alabama大学注册数据来说本文所提出的方法在测试阶段预测精度是比较好的，并且对未来数据的预测性能也是令人满意的。

5 结论

论域划分是影响模糊时间序列模型预测精度的关键因素,本文将改进的全局人工鱼群算法用于模糊时间序列论域的划分,从而提出了一种新的模糊时间序列预测模型,并将提出的方法用来预测Alabama大学注册人数,最后通过与其他模型进行比较，仿真结果表明：本文所提出的基于改进人工鱼群算法的模糊时间序列预测的有效性,它更好地反映了数据的结构,提高了预测精度。

参考文献：

[1]Zadeh L A.Fuzzy Sets[J].Information and Control,1965,8(3).

[2]Song Q,Chissom B S.Fuzzy Time Series and Its Models[J].Fuzzy Sets and Systems,1993,54(1).

[3]Song Q,Chissom B S.Forecasting Enrollments With Fu-Zzy Time Series:Part I[J].Fuzzy Sets and Systems,1993,54(1).

[4]Song Q,Chissom B S.Forecasting Enrollments With Fu-Zzy Time Series:Part II[J].Fuzzy Sets and Systems,1994,62(1).

[5]Sakhuja S,Jain V,Kumar S,et al.Genetic Algorithm Based Fuzzy Time Series Tourism Demand Forecast Model[J].Industrial Manage-ment&Data Systems,2016,116(3).

[6]Kuo I H,Horng S J,Kao T W,et al.An Improved Method for Forecasting Enrollments Based on Fuzzy Time Series and Particle Swarm Optimization[J].Expert Systems With Applications,2009,36(3).

[7]Kuo I H,Horng S J,Chen Y H,et al.Forecasting TAI FEX Based on Fuzzy Time Series and Particle Swarm Optimization[J].Expert Systems With Applications,2010,37(2).

[8]Bas E,Egrioglu E,Aladag C H,et al.Fuzzy Time Series Network Used to Forecast Linear and Nonlinear Time Series[J].Applied Intelligence,2015,43(2).

[9]Huarng K,Yu T H K.Ratio-Based Lengths of Intervals to Improve Fuzzy Time Series Forecasting[J].IEEE Transactions on Systems,Man and Cybernetics,Part B:Cybernetics,2006,36(2).

[10]Cheng S H,Chen S M,Jian W S.Fuzzy Time Series Forecasting Based on Fuzzy Logical Relationships and Similarity Measures[J].Information Sciences,2016,(327).

[11]Chen Y H,Hong W C,Shen W,et al.Electric Load Forecasting Based on a Least Squares Support Vector Machine With Fuzzy Time Series and Global Harmony Search Algorithm[J].Energies,2016,9(2).

[12]Cheng C H,Cheng G W,Wang J W.Multi-Attribute Fuzzy Time Series Method Based on Fuzzy Clustering[J].Expert Systems With Applications,2008,34(2).

[13]Chen S M.Forecasting Enrollments Based on Fuzzy Time Series[J].Fuzzy Sets and Systems,1996,81(3).

[14]Aladag C H,Yolcu U,Egrioglu E.A High Order Fuzzy Time Series Forecasting Model Based on Adaptive Expectation and Artificial Neural Networks[J].Mathematics and Computers in Simulation,2010,81(4).

[15]Chen S M.Forecasting Enrollments Based on High-Order Fuzzy Time Series[J].Cybernetics and Systems,2002,33(1).

[16]李晓磊,邵之江,钱积新.一种基于动物自治体的寻优模式:鱼群算法[J].系统工程理论与实践,2002,22(11).

[17]江铭炎,袁东风.人工鱼群算法及其应用[M].北京：科学出版社,2012.

[18]Chen S M,Chung N Y.Forecasting Enrollments Using High-Order Fuzzy Time Series and Genetic Algorithms[J].International Journal of Intelligent Systems,2006,21(5).

[19]Aladag C H,Basaran M A,Egrioglu E,et al.Forecasting in High Order Fuzzy Times Series by Using Neural Networks to Define Fuzzy Relations[J].Expert Systems With Applications,2009,36(3).

[20]陈刚,曲宏巍.一种新的模糊时间序列模型的预测方法[J].控制与决策,2013,28(1).

[21]Huang Y L,Horng S J,He M,et al.A Hybrid Forecasting Model for Enrollments Based on Aggregated Fuzzy Time Series and Particle Swarm Optimization[J].Expert Systems With Applications,2011,38(7).