波瓣喷嘴射流冲击平面靶板对流换热数值研究

王博滟，张靖周，吕元伟

(南京航空航天大学 能源与动力学院，江苏省航空动力系统重点实验室， 南京 210016)

射流冲击是一种极其有效的局部对流换热强化方法，在众多的工程领域中得到了广泛的应用，特别是在航空发动机热端部件高效冷却和进气道进口部件热气防冰结构设计中已成为主要的技术途径之一[1-3]。

射流冲击强化换热研究一直是国内外研究人员关注的热点问题，为改善射流冲击的传热强化效果，提出了包括形状喷嘴、处理靶面、涡旋激励、脉冲间断等多种被动或主动的技术措施[4]。大量研究表明，喷嘴形状由于改变了射流剪切层结构和卷吸掺混过程而对射流冲击换热形成显著的影响[5-8]，近年来利用喷嘴出口涡激励结构增强射流冲击对流换热更为研究人员所关注[9-12]。

波瓣形喷管是一种具有高效掺混效应的喷管构型，在发动机排气系统中得到了广泛应用[13]。针对波瓣喷管的射流流动机制以及结构参数影响规律已开展了较为系统的研究[14-18]，由于其褶曲的波瓣结构诱导出大尺度流向涡，可以有效地增强同轴射流之间的混合。近年来，研究人员对利用波瓣流向涡特征增强射流的传质和传热也开始有所关注，Nastase等[19]研究了用波瓣射流的涡结构及其卷吸效应，指出波瓣形状对于射流剪切和核心区流动具有重要的影响作用；Herrero等[20]开展了3瓣和4瓣喷嘴的射流冲击换热实验研究，研究结果表明在高射流雷诺数下波瓣喷嘴能有效增强对流换热。

目前，针对波瓣射流冲击换热特性的研究尚十分缺乏，特别是波瓣射流相对于常规射流是否具有显著的增强作用及其影响机制，仍需要进行探究。鉴于此，本文针对一个特定的6波瓣喷嘴，研究在典型的射流雷诺数下冲击间距对波瓣射流冲击换热的影响，并与圆形射流进行对比分析。

1 计算模型

针对单股射流冲击靶面建立相应的物理模型，如图1所示，冲击射流通过喷嘴垂直冲击到平面靶板，形成壁面射流。本文研究了具有相同入口和出口截面积的波瓣喷嘴和圆形喷嘴冲击射流，其中波瓣喷嘴与圆形喷嘴的出口面积相等。喷嘴入口直径d=10 mm，冲击射流雷诺数Re分别取值为10 000、16 000和20 000。喷嘴出口至冲击靶面的间距与喷管直径之比H/d取为2、4、6和8。

射流冲击至靶面形成驻点区并沿靶面径向形成壁面射流区。鉴于射流冲击的局部强化传热特征，主要关注冲击驻点下游5d左右范围内(即r/d≈5)的对流换热特性[1,4]，因此本文在计算域设置上，为了使壁面射流有相应的径向发展空间，选取20倍射流管直径作为冲击靶面直径。

图2所示为波瓣喷嘴结构示意图。波瓣喷嘴的6个波瓣沿周向均匀分布，波瓣全扩张角(α)为30°，波瓣内、外包络线半径分别为Rin=2.55 mm和Rout=7.5 mm，瓣宽b为2 mm，波瓣轴向长度L2为10 mm，射流管长度L1+L2为70 mm。

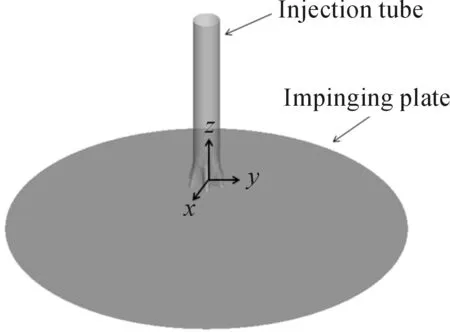
图1 射流冲击靶板示意图

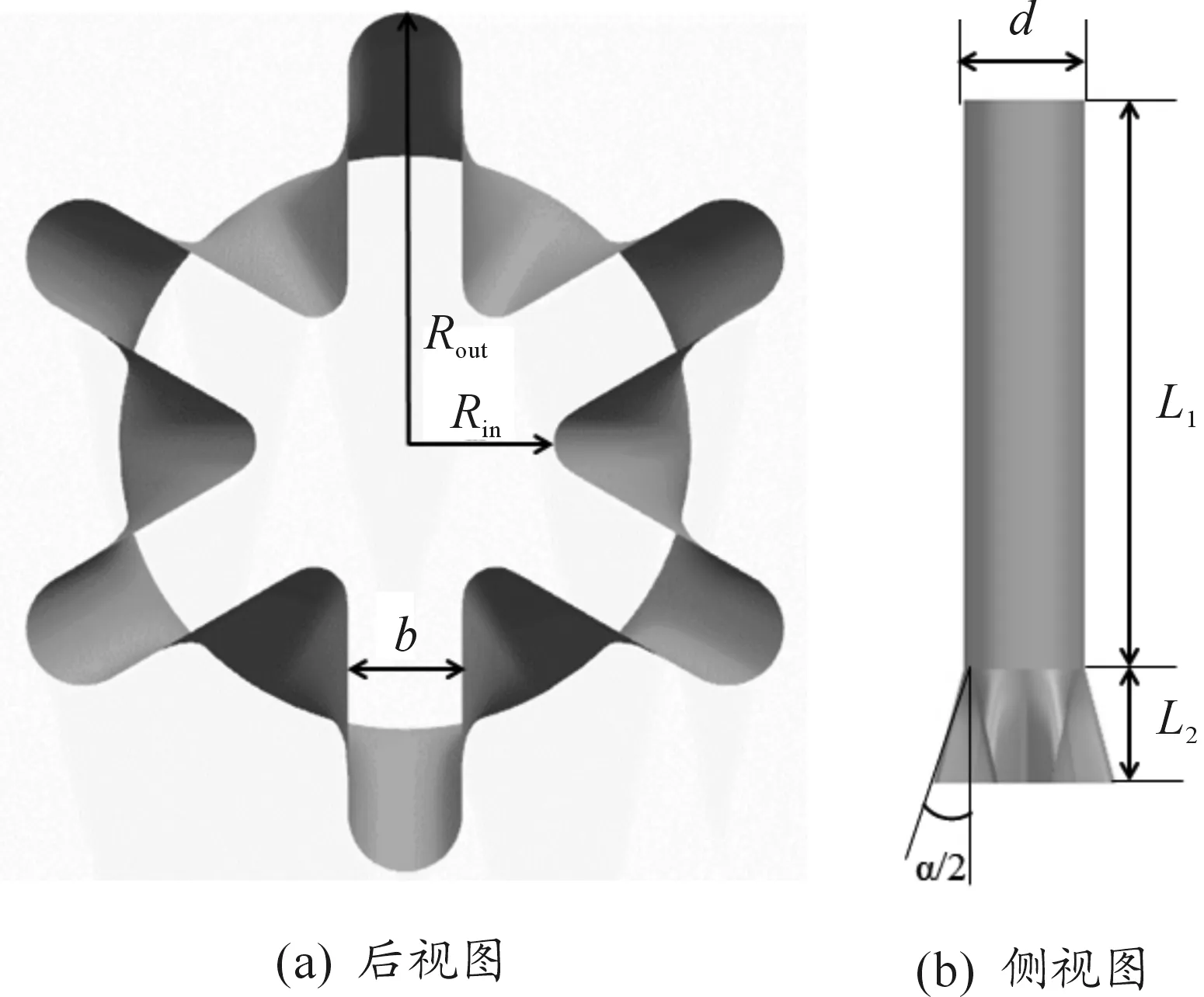
图2 波瓣喷嘴结构示意图

2 计算方法

2.1 网格划分和边界条件

鉴于波瓣的褶曲型面，计算网格划分采用结构化与非结构化混合的网格系统，即在波瓣喷嘴内部和外侧附近采用非结构型网格，而在离开喷嘴外侧一定距离后采用结构化网格进行划分。同时在固体壁面附近采用附面层网格加密。图3为网格示意图。在计算过程中，对计算模型的网格无关性进行了预先分析，以Re=10 000、H/d=2时波瓣射流冲击平板模型的网格独立性测试为例，计算域内网格数分别选取100万、150万、200万、280万和350万，其网格的差异在于壁面附近和波瓣内部的网格加密区。图4为网格数对靶板驻点处Nu数的影响，经网格独立性测试，确定网格数取为200万左右。

在计算过程中，边界条件设置如下：冲击射流介质为空气，进口采用质量流量进口，对应的射流冲击雷诺数分别为10 000、16 000和20 000；冲击靶面为零厚度，采用无滑移壁面边界条件，恒热流密度(q)设为4 000 W/m2；喷嘴壁面采用无滑移绝热边界条件，外流场边界设为压力出口，静压为101 325 Pa。射流温度为300 K，鉴于在本文研究的参数条件下，气流温度变化不大，因此在计算过程中不考虑壁面冷却过程中温度变化导致的空气热物性变化。

应用Fluent软件进行三维雷诺时均控制方程(RANS)的稳态数值计算。采用二阶迎风格式进行数值离散，压力-速度耦合采用SIMPLEC方法，收敛的标准是各项残差精度均小于10-5，残差曲线趋于平直且靶板表面的温度不再变化。

图3 计算网格示意图

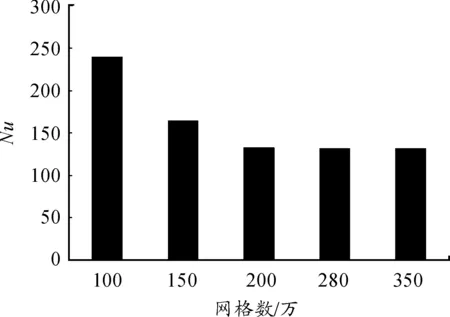
图4 网格独立性验证

2.2 湍流模型和计算方法验证

选择Violato等[10]的圆形射流冲击平板的实验模型进行计算方法验证，实验中的冷却介质为空气。计算中分别选取Realizablek-ε和RNGk-ε湍流模型进行湍流模化。图5为射流雷诺数为5 000、冲击间距比为6时，沿径向的平均Nu数计算结果与实验数据对比，可以看出，2种湍流模型对射流冲击驻点区的对流换热均存在一定的“过-预测”，相形之下，Realizablek-ε模型在射流冲击驻点区的计算结果较接近实验值，与实验值的误差在10%以内。同时，考虑到Realizablek-ε模型已被众多研究者应用于波瓣强迫混合流场和射流冲击换热的数值研究[21-23]，所以，本文采用Realizablek-ε模型，在壁面附近选用增强壁面函数进行数值模拟。

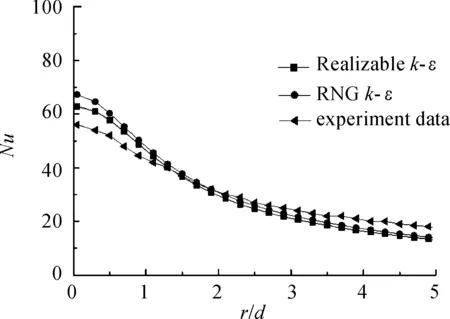
图5 湍流模型验证

3 结果与分析

3.1 流动特征

图6所示为Re=10 000时射流在离开喷口下游0.1d截面上的速度矢量图。对于圆形射流，由于剪切作用周围的流体向射流核心区迁移，如图6(a)所示；而对于波瓣射流，由于波瓣波峰的扩张型面诱导射流形成径向向外的流动，在波瓣波谷对应的区域周围流体形成更为明显的向内卷吸，如图6(b)所示。很显然，波瓣射流与周围流体的掺混卷吸作用显著高于圆形射流，与前人揭示的波瓣射流流动特征一致。

图7为Re=10 000时波瓣喷嘴流向涡在喷口下游发展的计算结果。可以看到，在邻近喷口下游波瓣诱导出很强的流向涡对，随着射流的发展，流向涡强度逐渐衰减、作用范围有所扩大，在喷口下游4倍射流管直径处，流向涡的强度已经很微弱，表明周向掺混已趋于均匀。

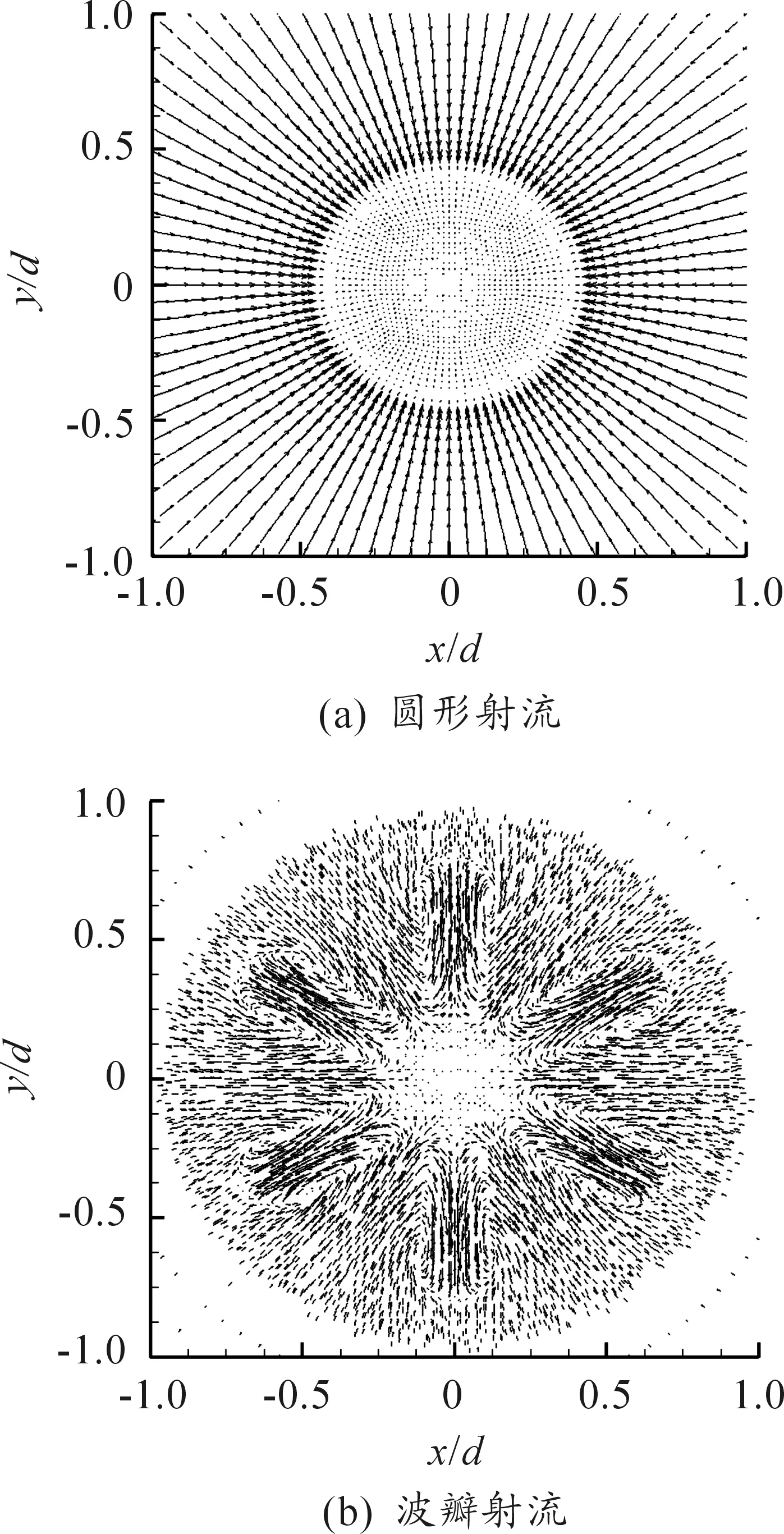
图6 距喷口下游0.1d的x-y平面上速度矢量图

图7 Re=10 000波瓣喷嘴流向涡分布云图

由于波瓣喷嘴在射流出口下游诱导出阵列的流向涡，强化了射流对周围流体的卷吸，因此射流的发展与常规圆形射流具有较大的差异。针对射流冲击问题，波瓣射流的发展及其与圆形射流的差异随射流冲击间距的改变而发生变化。图8和图9分别为Re=10 000时，H/d=2和H/d=6时射流法向速度剖面沿程变化，图中参考速度u0为喷口的射流平均速度。

在紧邻喷口下游法向距离上，H/d=2和H/d=6时的速度剖面具有近乎完全的一致性，如图8(a)和图9(a)所示，相对于圆形射流的速度剖面，波瓣射流在波峰上更为饱满，而在波谷上则相对狭窄。同时，由于波瓣相对圆形具有更长的周长，射流在管内的流动附面层效应更为显著，因而导致射流核心区内的速度略高于圆形射流。然而，射流在趋向冲击靶板时的速度分布则与射流冲击间距不同而形成极大的区别。

对于小冲击间距，波瓣射流在发展中尚不能形成周向的充分混合，如图8(b)所示，速度分布在波瓣波峰和波谷方向上的差异明显；在距离靶面z/d=0.3的截面上，如图8(c)所示，圆形射流的峰值速度略偏于射流中心，这是由于射流与壁面射流相互作用的缘故。此时，波瓣射流在中心区则体现出更高的趋近速度，且在波瓣波峰和波谷方向上的速度分布依然维持着一定的差异。

对于大冲击间距，如图9(b)所示，在喷口下游4倍射流管距离处，波瓣射流在波峰和波谷上的差异已趋于消失。在距离靶面z/d=0.3的截面上，如图9(c)所示，波瓣射流的速度分布更为平缓且中心速度低于圆形射流，体现了大尺度的流向涡加剧周向掺混、缩减射流核心区长度的作用机制[14]。

图8 Re=10 000和H/d=2时沿程射流法向速度剖面

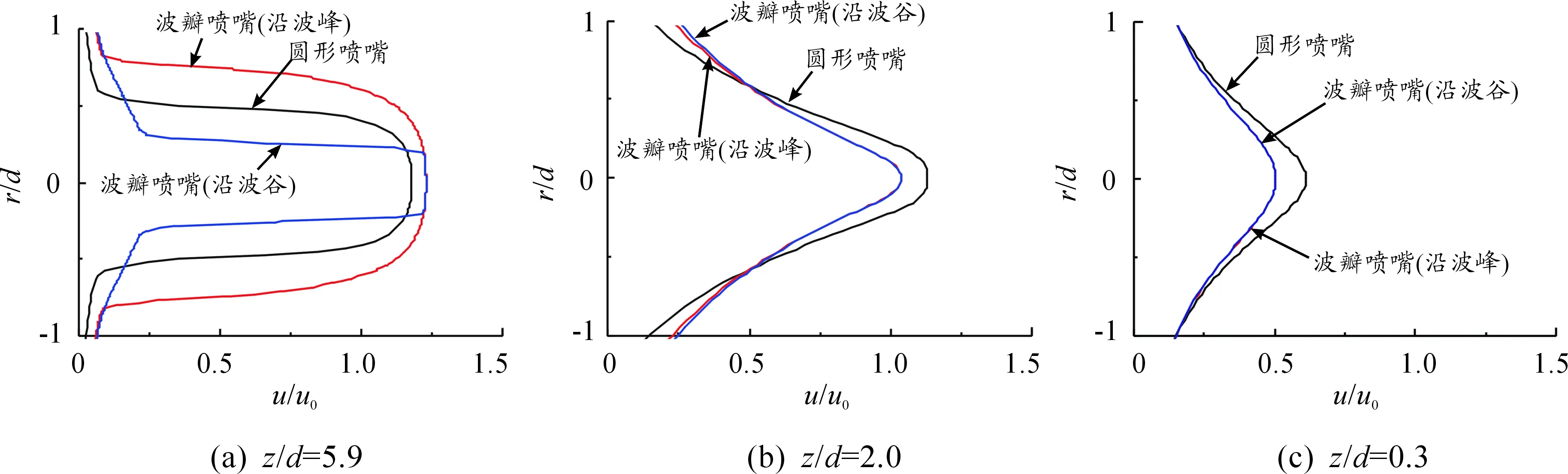
图9 Re=10 000和H/d=6时沿程射流法向速度剖面

3.2 对流换热特性

图10和图11分别为Re=10 000时，H/d=2和H/d=8时冲击靶面局部Nu数的分布。

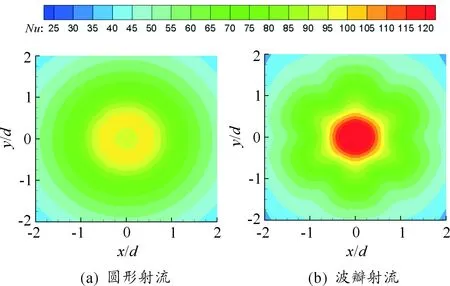
图10 Re=10 000和H/d=2时局部Nu数分布

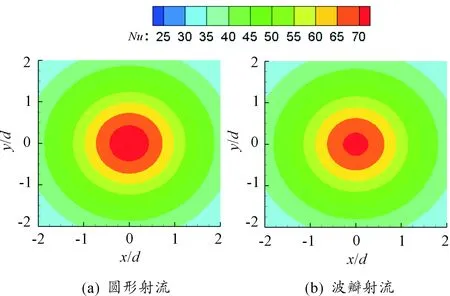
图11 Re=10 000和H/d=8时局部Nu数分布

在小冲击间距下，圆形射流的峰值对流换热系数出现在略偏于射流中心的圆环中，与其射流趋近速度分布相对应，这一现象与前人揭示的小冲击间距下峰值对流换热系数偏移的研究结果相一致[24]。对于波瓣射流冲击，中心的对流换热显著高于圆形射流冲击，且在中心区外缘呈现明显的波瓣形分布。在大冲击间距下，波瓣喷嘴与圆形喷嘴的Nu数分布趋于一致，相对于小冲击间距对流换热有较大的降低，对于波瓣喷嘴而言，相对降低的幅度更为显著。

图12为不同射流冲击间距下波瓣射流和圆形射流冲击下的周向平均Nu沿径向的分布曲线。这里，周向平均Nu定义为：

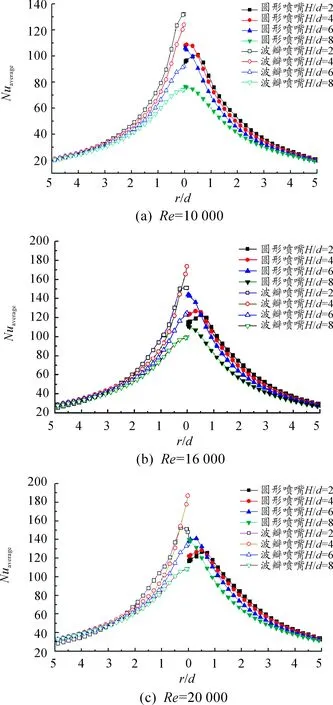
图12 不同射流冲击间距下周向平均Nu数分布

可以看出，波瓣射流冲击相对于圆形射流的对流换热效果与射流冲击间距密切相关。

不同冲击雷诺数下，2种喷嘴射流的冲击换热规律都存在较大差别。当射流Re为10 000时，对于圆形射流冲击，射流驻点区的对流换热在H/d=4～6时最优，与已有的自由射流冲击换热研究结论相符[4]；对于波瓣射流冲击，随着射流冲击间距的增加，射流驻点区的对流换热呈现逐渐降低的趋势；当射流Re达到16 000和20 000时，圆形射流冲击驻点区对流换热的最佳冲击间距比为6，而波瓣射流冲击驻点区对流换热的最佳冲击间距比则为4。

总体而言，在小冲击间距下(H/d=2和4)，波瓣射流冲击的对流换热显著高于圆形射流，随着冲击间距的增加，波瓣射流相对于圆形射流的对流换热强化优势迅速下降；当冲击间距比达到6和8时，波瓣射流在射流驻点区的冲击对流换热则弱于圆形射流冲击。

4 结论

采用数值计算方法，对比研究了波瓣喷嘴和圆形喷嘴在射流雷诺数(Re)为10 000～20 000、冲击间距比(H/d)为2～8范围内的射流冲击平面靶板对流换热。结果表明：

1) 波瓣喷嘴在射流出口下游诱导出阵列的流向涡，强化了射流对周围流体的卷吸，射流的发展与常规圆形射流具有较大的差异，因而导致对流换热的差异，与射流冲击间距密切相关。

2) 在小冲击间距比下(H/d=2和4)，波瓣射流趋向冲击靶面的核心区速度高于圆形射流，且在波瓣波峰和波谷方向上的速度分布维持着一定的差异，因而相对于圆形射流具有更高的驻点对流换热能力，中心区外缘的局部对流换热系数呈现波瓣状分布。

3) 在大冲击间距比下(H/d=6和8)，波瓣射流趋向冲击靶板附近的速度分布更为平缓且中心速度低于圆形射流，小冲击间距比下出现的局部对流换热系数波瓣状分布消失。波瓣射流在驻点区的冲击对流换热弱于圆形射流冲击。

参考文献：

[1] WEIGAND B,SPRING S.Multiple jet impingement—a review [J].Heat Transfer Research,2011,42:101-142.

[2] 刘友宏,李英,杨旭.冲击/发散冷却层板隔热屏冷却性能及对比[J].航空动力学报,2014,29(6):1272-1278.

[3] 关涛,张靖周,单勇,等.楔形凹腔内带前伸槽冲击板射流冲击换热[J].航空动力学报,2017,32(3):592-598.

[4] CARLOMAGNO G M,IANIRO A.Thermo-fluid-dyna-mics of submerged jets impinging at short nozzle-to-plate distance:A review [J].Experimental Thermal and Fluid Science,2014,58:15-35.

[5] COLUCCI D W,VISKANTA R.Effect of nozzle geometry on local convective heat transfer to a confined impinging air jet [J].Experimental Thermal and Fluid Science,1996,13:71-80.

[6] LEE J H,LEE S J.The effect of nozzle configuration on stagnation region heat transfer enhancement of axisymmetric jet impingement [J].International Journal of Heat and Mass Transfer,2000,43:3497-3509.

[7] ROYNE A,DEY C J.Effect of nozzle geometry on pressure drop and heat transfer in submerged jet arrays [J].International Journal of Heat and Mass Transfer,2006,46:800-804.

[8] GULATI P,KATTI V,PRABHU S V.Influence of the shape of the nozzle on the local heat transfer distribution between smooth flat surface and impinging air jet [J].International Journal of Thermal Sciences,2009,48:602- 617.

[9] YANG H Q,KIM T,LU T J,et al.Flow structure,wall pressure and heat transfer characteristics of impinging annular jet with/without steady swirling [J].International Journal of Heat and Mass Transfer,2010,53:4092-4100.

[10] VIOLATO D,IANIRO A,CARDONE G,et al.Three-dimensional vortex dynamics and convective heat transfer in circular and chevron impinging jets [J].International Journal of Heat and Fluid Flow,2012,37:22-36.

[11] YU Y Z,ZHANG J Z,XU H S.Convective heat transfer by a row of confined air jets from round holes equipped with triangular tabs [J].International Journal of Heat and Mass Transfer,2014,72:222-233.

[12] GUAN T,ZHANG J Z,SHAN Y.Convective heat transfer by tab-excited impinging jets on a wedge-shaped concave surface [J].International Journal of Thermal Sciences,2016,100:37-53.

[13] PATERSON R W.Turbofan mixer nozzle flow field-a benchmark experimental study [J].ASME Journal of Engineering Gas Turbines and Power,1984,106:692-698.

[14] MCCORMICK D C,BENNETT J C.Vortical and turbulent structure of a lobed mixer free shear layer [J].AIAA Journal,1994,32:1852-1859.

[15] HU H,SAGA T,KOBAYASHI T,et al.A study on a lobed jet mixing flow by using stereoscopic particle image velocimetry technique [J].Physics of Fluids,2001,13:3425-3441.

[16] 单勇,张靖周.波瓣喷管结构参数对引射混合器性能影响的数值研究[J].航空动力学报,2005,20(6):197-201.

[17] 丁玉林,刘友宏,谢翌,等.尾缘锯齿修形对波瓣强迫混合排气系统性能影响[J].航空动力学报,2012,27(10):2236-2242.

[18] 岳巍,雷志军,苏尚美,等.波瓣混合器涡系结构及射流掺混机理的数值研究[J].航空动力学报,2013,28(2):338-346.

[19] NASTASE I,MESLEM A.Vortex dynamics and mass entrainment in turbulent lobed jets with and without lobe deflection angles [J].Experimental Fluids,2010,48 693-714.

[20] HERRERO M R,BUCHLIN J M.Jet impingement heat transfer from lobed nozzles [J].International Journal of Thermal Sciences,2011,20:1199-1206.

[21] COOPER N J,MERATI P,HU H.Numerical simulation of the vertical structure in a lobed jet mixing flow[R].AIAA Paper 2005-635,2005.

[22] SINGH D,PREMACHANDRAN B,KOHLI S.Experimental and numerical investigation of jet impingement cooling of a circular cylinder [J].International Journal of Heat and Mass Transfer,2013,60:672-688.

[23] GUAN T,ZHANG J Z,SHAN Y,et al.Conjugate heat transfer on leading edge of a conical wall subjected to external cold flow and internal hot jet impingement from chevron nozzle-part 2:numerical analysis[J].Internatio-nal Journal of Heat and Mass Transfer,2017,106:339-355.

[24] VISKANTA R.Heat transfer to impinging isothermal gas and flame jets [J].Experimental Thermal Fluid Science,1993,6:111-134.