用离散化方法证明半定规划的拉格朗日强对偶定理
2018-05-10罗洪林
罗 丹,罗洪林
(重庆师范大学 数学科学学院, 重庆 401331)
1 背景

(P) mincTx
s.t.F(x)≥0
半定规划也称为带有半正定锥约束的线性规划,其退化情形包括线性规划和凸二次规划。半定规划广泛地存在于系统与控制理论[1]、金融工程[2]、量子化学[3]、信号处理[4]等诸多领域。 半定规划的多项式内点算法为求解组合优化领域的某些中小规模的NP难问题(如著名的旅行商问题[5]和最大割问题[6])提供了有效的解决途径。 自20世纪90年代初期至今,半定规划一直是优化领域的一个热门的研究课题。
半定规划的对偶理论在半定规划的理论研究和算法设计中都扮演着十分重要的角色。半定规划的对偶理论研究除了常见的拉格朗日对偶和共轭对偶理论外,具有代表性的包括Ramana等提出的广义拉格朗日slater对偶理论[7]和极小锥对偶理论[8]。 本文主要从算法的角度重新考察半定规划的拉格朗日对偶理论。
原始半定规划问题(P)的拉格朗日对偶模型为:
(D) max -TrF0Z
s.t.TrFiZ=ci,i=1,…,m
Z≥0
记val(D)为(D)的最优目标函数值, 称(D)可行是指其可行域非空,即:存在Z≥0使得TrFiZ=ci,i=1,…,m; 称(D)严格可行是指存在Z>0使得TrFiZ=ci,i=1,…,m成立。
内点算法是求解中小规模的半定规划的十分有效的求解算法。内点算法利用半定规划的原始对偶模型的1阶最优性条件(KKT条件)建立可行或不可行中心路径的方式提出了各种可行内点算法和不可行内点算法。 最近,杨洋等[9]利用不可行中心路径给出了一种宽领域不可行内点算法。 内点算法由于需要储存和分解牛顿矩阵,这将占用大量的内存空间且十分耗时,在2002年,Helmberg[10]指出:在一般的计算机处理系统上通过合理的等待时间,用内点算法能有效计算的半定规划问题,其矩阵变量n≤200,约束的个数m≤3 000。 截至2013年,Huang等[11]指出,目前的内点算法一般可以有效求解的中小规模的半定规划的矩阵变量n≤1 000,约束的个数m≤10 000。
如何为大规模的半定规划问题设计有效的求解算法是一个有待解决的问题。 为了摆脱牛顿矩阵的储存和分解,受Yang[12]的启发,本文将从强对偶定理的一种新的证明方法来阐述半定规划的一种新的求解算法。
本文的第1部分利用离散化方法将半定规划问题近似地转换为一个线性规划问题并给出了2个问题的最优解的近似程度的刻画。本文的第2部分给出了强对偶定理的一个新的证明方法以及半定规划的一种新的离散化求解算法及其收敛性证明。 针对本文提出的半定规划的一种新的理论算法,在第3部分提出了该算法数值实现时可能面临的几个待解决的问题。 附录部分呈现了半定规划的强对偶定理的经典证明过程以方便读者比较它与离散化证明方法之间的异同。
2 半定规划的离散化方法
本节主要介绍对偶半定规划(D)的离散化方法以及(D)的最优解与离散化问题的最优解之间的误差刻画。为了半定规划的离散化方法的描述完整性,首先引入Yang[12]关于原始半定规划问题(P)的离散化过程:
第1步利用{x∈Rm|F(x)≥0}与{x∈Rm|yTF(x)y≥0,∀y∈Rn}的等价性,将(P)等价地转化为如下形式的优化问题:
mincTx
s.t.yTF(x)y≥0
y∈Rn
(1)
第2步将集合{y∈Rn|yTF(x)y≥0}正则化为{y∈Rn|yTF(x)y≥0,yTy=1},则问题(1)可等价地表示为如下的线性半无限规划问题:
mincTx
s.t.aT(y)x+b(y)≥0
y∈Y
(2)
其中Y={y∈Rn|yTy=1},aT(y)=(yTF1y,yTF2y,…,yTFmy),bT(y)=yTF0y
记
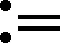
问题(2)关于κ∈R的下水平集定义为:
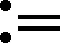
第3步选取有限网格Yd⊂Y离散化问题(2),得到一个线性规划问题:
mincTx
s.t.aT(y)x+b(y)≥0
y∈Yd
(3)
网格Yd与集合Y的Hausdorff距离定义为
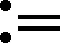
记
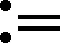
通过上述离散化方法可将(P)近似地转换为一列线性规划问题进行近似求解,求解的精度取决于网格Yd的取法,具体参见文献[12]中的引理2。
众所周知,不论是半定规划还是线性规划,研究其对偶理论的主要目的之一就是化解问题求解的难度,即:相较于原问题,当对偶问题的求解更加容易时,在强对偶定理的理论支撑下,可以通过求解其对偶问题而获得原问题的解。基于此,利用Dattorro[13]中的:
(4)
给出对偶半定规划问题(D)的离散化过程:
第1步利用等式(4)将对偶半定规划问题(D)等价地转化成如下形式的优化问题:
(5)
第2步通过bj≥0,j=1,2,…的适当选取(仍然记为bj≥0,j=1,2,…),将向量zj∈Rn,j=1,2,…单位化,则式(5)可等价地转换为:
(6)
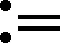
记
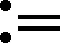
i=1,…,m,zj∈Z′}
问题(6)关于λ∈R的下水平集定义为:
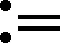
第3步选取有限网格Zk⊂Z′,不妨设Zk含有k个向量z1,z2,…,zk,则与之对应的k个非负实数为b1,b2,…,bk,现通过该网格离散化问题(6)得到一个线性规划问题:
(7)
网格Zk与集合Z的Hausdorff距离定义为:
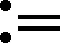
记
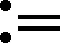
i=1,…,m,z∈Zk}
为了利用离散化方法证明半定规划的强对偶定理,需要建立以下几个结论:
定理1 如果(P)严格可行,(D)可行,那么对任意给定的λ∈R,水平集
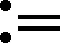
有界。
证明假设存在一个λ0∈R使得水平集
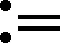
无界,则存在非负数列{bj}⊂L≥(BD(Z),F0,λ0)满足:
(8)
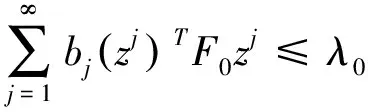
(9)
且
zj∈Z′={z∈Rn|||z||=1}=Y
对任意给定的y∈Y,则存在序列{vj}满足

(10)
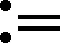
(11)
由级数收敛的必要条件和式(9)可得:
再结合式(10)以及式(11)可推得:
yTF0y=0,∀y∈Y
(12)

(13)

(14)
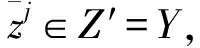
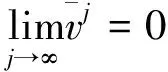
(15)
由级数收敛的必要条件和(ref{eq7})可得:
再结合式(14)与(15)可推得:
yTFiy=0,∀y∈Y,i=1,2,…,m
(16)
故,由式(12)和(16)可得:
∀y∈Y
由于(P)与式(2)等价,不难发现上式与半定规划问题(P)的严格可行性假设矛盾。
由于(D)的严格可行性必蕴含其可行性,则由定理1可得如下推论:
推论1 问题(P)和(D)都严格可行,则对λ∈R,水平集
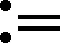
有界。
命题1 若问题(P)和(D)都严格可行,则对κ∈R,水平集
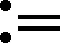
有界。
证明由Yang[12]中的引理1和半定规划(P)严格可行性蕴含问题的可行性得结论成立。
如下2个命题揭示了:用离散化方法可以求得半定规划问题(P)和(D)满足任意精度的近似解。
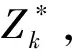
证明因为(P)与式(2)等价,(D)与式(6)等价,由定理1及文献[14]中的定理4.4可以证得。
类似地,可以利用推论2和命题1以及文献[14]中的定理4.4可以证明下面这个命题:
命题3 若问题(P)和(D)都严格可行,那么,
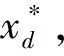
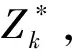
3 强对偶定理的离散化证明方法及其在算法设计中的应用
当半定规划问题(P)和(D)满足一定的条件时,若能推出对偶间隙:
val(P)-val(D)=0
则称为半定规划的强对偶定理。 关于半定规划的强对偶定理的经典证明方法请参见附录。2005年,Yang[12]通过原始半定规划(P)的离散化方法证明了在原始半定规划(P)可行和对偶半定规划(D)严格可行的假设条件下的强对偶定理。 值得指出的是,可以利用Yang[12]关于原始半定规划(P)的离散化方法为(P)的求解设计一种新的求解算法:利用文献[14-15]中关于半无限规划的离散化算法近似地求解(P)。
下面利用对偶半定规划问题(D)的离散化方法重新给出半定规划的另外2个强对偶定理的证明,进而为对偶半定规划问题(D)设计一种新的求解算法。
3.1 强对偶定理的证明
定理2 如果(P)严格可行,(D)可行,则val(P)=val(D),且(D)的最优解Z*最优可达。
证明定理1可知,对任意给定的λ∈R,水平集L≥(BD(Z),F0,λ)是有界闭的,则L≥(BD(Z),F0,λ)是紧集且当λ充分大时非空。 因此,(D)的最优解可以在可行域中取到。
现定义网格Zk={z1,z2,…,zk},则式(7)可以等价地表示成如下形式的线性规划问题:
(17)
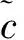
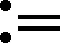
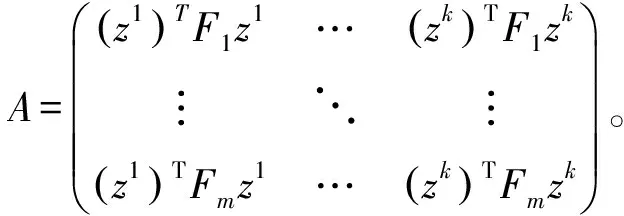
maxcTx
s.t.aT(yj)x+b(yj)≥0
yj∈Yk,j=1,…,k
(18)
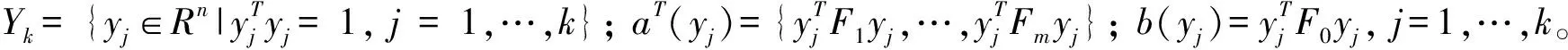
由半定规划的弱对偶定理有:
val(P)≥val(D)
(19)
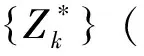
(20)
因此,对于充分小的dZk,val(Zk)有界。故由线性规划的强对偶定理,有
val(Zk)=val(xk)
(21)
由于(P)的可行解包含式(18)的可行解,则有
val(P)≤val(xk)
(22)
结合式(20)、(21)和(22),令dYk→0可得:
val(P)≤val(D)
(23)
综合式(19)和(23)得: val(P)=val(D)
定理3 如果(P)和(D)都严格可行,则 val(P)=val(D),且(P)的最优解x*和(D)的最优解Z*都最优可达。
证明由命题1和推论1可知,对任意给定的λ∈R,水平集L≥(XP(Y),c,κ)和L≥(BD(Z),F0,λ)是有界闭的,则L≥(XP(Y),c,κ),L≥(BD(Z),F0,λ)是紧集且分别当κ、λ充分大时非空。 因此,(P)和(D)的最优解可以在其各自的可行域中取到。
现定义网格Zk={z1,z2,…,zk},则式(7)可以等价地表示成如下形式的线性规划问题:
(24)
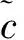
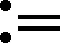

maxcTx
s.t.aT(yj)x+b(yj)≥0
yj∈Yk,j=1,…,k
(25)
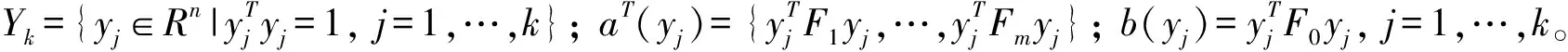
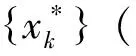
(26)
(27)
因此,对于充分小的dYk, val(xk)有界;对于充分小的dZk, val(Zk)有界。 故由线性规划的强对偶定理,有
val(Zk)=val(xk)
(28)
结合式(26)、(17)和(28),令dYk→0,dZk→0可得:
val(P)=val(D)
(29)
3.2 半定规划的离散化算法
求解一般的中小规模的半定规划问题时可以用CVX[16]中的SDPT3或SeDuMi求得满足任意精度的近似解。 不论是SDPT3还是SeDuMi,其求解原理都是利用原始对偶内点算法,需要储存和分解牛顿矩阵,这将占用大量的内存空间且十分耗时。
根据文献[14]对半无限规划问题的离散化算法的描述,当(P)严格可行,(D)可行,针对对偶半定规划问题(D),设计如下算法:
算法1 首先将半定规划对偶问题(D)转换为等价的线性半无限规划问题(16),然后,给定一个步长向量h∈Rm,其中hj>0,j=1,…,m,并且固定一个z0∈Rm,定义网格
Gh={z|(z-z0)j=αjhj,αj∈N,j=1,…,m}
并且
Zh=Z∩Gh
具体步骤如下:

① 设hi+1=(1/ni)hi,ni∈N,ni≥2。
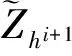
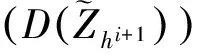
④ 如果i>i0(预先规定步数)则停止,否则继续第(i+1)步。
注:1) 该离散化方法在求解对偶半定规划问题(D)时,无需储存和分解牛顿矩阵;
下面简单地给出该算法的收敛性证明。
4 结论和展望
利用离散化方法,本文给出了强对偶定理的一种新的证明方法,并利用该方法设计了一种半定规划的求解算法。 本文仅从理论上给出了半定规划的求解算法及其收敛性分析,值得指出的是,虽然该算法摆脱了传统的内点算法对于牛顿矩阵的储存和分解,但是在算法步骤中涉及随机变量,这可能会导致数值实验结果的不稳定性。若让算法中的随机变量满足一定的概率分布,对于满足均匀分布或标准正态分布等是否可以使得数值实验结果更加稳定, 如何改进该算法以适用于有效地求解大规模的半定规划问题, 这些是接下来准备研究的问题。
参考文献:
[1] YAO D,ZHANG S Z,ZHOU X Y.Control theory stochastic linear-quadratic control via semidefinite programming [J].Society for Industrial and Applied Mathematics,2001,40:1-23.
[2] DALAKOURAS G V,KWON R H,PARDALOS P M.Semidefinite programming approaches for bounding asian option prices [J].Computational Methods in Financial Engineering,2008,103-116.
[3] DING Y,GE D,WOLKOWICZ H.On equivalence of Semidefinite relaxations for quadratic matrix programming [J].Mathematics of Operations Research,2011,36:8-104.
[4] BISWAS P,TOH K C,YE Y.A distributed Semidefinite approach for large-scale noisy anchor-free graph realization with applications to molecular conformation [J].Society for Industrial and Applied Mathematics,2008:1251-1277.
[5] KLERK E D,PASECHNIK D V,SOTIROV R.On semidefinite programming relaxations of the traveling salesman problem [J].Society for Industrial and Applied Mathematics,2008,19:1559-1573.
[6] GRIPPO L,PALAGI L,PICCIALLI V.An unconstrained minimization method for solving low-rank SDP relaxations of the maxcut problem [J].Mathematical Programming,2011,126:119-146.
[7] RAMANA M V.An exact duality theory for semidefinite programming and its complexity implications [J].Mathematical Programming,1997,77:129-162.
[8] Ramana M V,Tuncxelz L,Wolkowicz H.Strong duality for semidefinite programming [J].Society for Industrial and Applied Mathematics,1997,7(3):641-662.
[9] 杨洋,罗洪林,罗慧林.关于半定规划的一种宽邻域不可行内点算法的注记 [J].运筹学学报,2016,20(2):79-87.
[10] HELMBERG C.Invited Review,Semidefinite programming [J].European Journal of Operational Research,2002,137:461-482.
[11] HUANG A Q,XU C X.A trust region method for solving semidefinite programs [J].Computational Optimization and Applications,2013,55:49-71.
[12] YANG Q Z.A new proof of the strong duality theorem for semidefinite programming [J].it Mathematical analysis and applications,2005,303:622-626.
[13] DATTORRO J.Convex optimization and euclidean distance geometry[Z].Meboo Publishing USA,2005.
[14] HETTICH R,KORTANEK K O.Semi-infinite programming:Theory,methods,and application [J].Society for Industrial and Applied Mathematics,1993,35:380-429.
[15] HETTICH R.An implementation of a discretization method for semi-infinite programming [J].Math Programming,1986,34:354-361.
[16] GRANT M,BOYD S.The CVX Users’ Guide (Release 2.0 (Beta))[EB/OL].[2018-01-01].http://cvxr.com/cvx/(221) March 2013.
[17] ALIZADEH F.Interior point methods in semidefinite programming with applications to combinatorial optimization [J].Society for Industrial and Applied Mathematics,1995,5:13-51.
附录A
定理4[17]令
z1=inf{C·X:Ai·X=bi,X≥0}
z2=sup{bTy:C-∑yiAi≥0}
如果存在一个m维向量y,使得ATy>0,那么z2=z1。
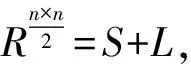
Mat(ATy1)≤0且bTy1>0
意味着对偶问题是无界的。由于任意的对偶可行解y能增加一个任意大的正乘子在y1前,得到另一个可行解有巨大的目标函数值。 因此,z2=z1=+∞。 可以假设z1和z2都是有限的, 假设z2 C·X=z2 AvecX=b X≥0 是不可行的。 因此,通过推广的Farkas引理2.3,存在一个标量y0和m维向量y,使得 且z2y0+bTy<0 (19) 其中vecAi是A的第i行。 对y0,下列之一成立。 1) 若y0=0,式(19)等价于 Mat(ATy)≤0 且bTy>0 通过推广的Farkas引理得AvecX=b且X≥0是不可行的, 因此z1=+∞。 2) 若y0=0,则式(19)除以y0得 C-Mat(AT(-y/y0))≥0且 z2-bT(y/y0)<0 意味着z2不是对偶问题的最优值。 3) 若y0<0,则式(19)除以-y0得 -C+Mat(AT(-y/y0))≥0且 -z2+bT(-y/y0)<0 事实上,由于是严格不等式,则存在ε>0,使得 -C+Mat(AT(-y/y0))≥0且 -z2+bT(-y/y0)<-ε 同样地,通过z2的最优性,存在一个y*,使得 C-Mat(ATy*)≥0且z2-bTy*<ε 最后2个式子相加得 Mat(AT(-y/y0-y*))≥0且 bT(-y/y0-y*)<0 再次通过推广的Farkas引理得原问题不可行且z1=∞,与假设z2
