加速度计标定中静态半径误差项的消除技术

黄钦文，杨少华,2，董显山，王蕴辉

（1. 工业和信息化部电子第五研究所 电子元器件可靠性物理及其应用技术重点实验室，广州 510610；2. 广东工业大学 物理与光电工程学院，广州 510006）

在加速度计的研制、生产和使用中，都需要对加速度计的性能进行校准。加速度计在±1g以内的各项性能指标可利用重力场翻滚试验设备进行测试，但测量范围局限于±1g以内，因此，在重力场1g范围内对加速度计的高阶项系数进行标定时可信度不高。而精密离心机能够持续提供恒定的大于 1g的加速度值，是测试、标定加速度计在高g值条件下性能的重要设备，能够提高高g条件下对加速度计的标定精度[1-8]。

然而，与重力场翻滚测试方法相比，基于离心机的测试标定方法存在新的问题需要解决，其重点和难点之一是确定被测加速度计的真实静态半径。由于加速度计的有效质量中心（effective center of mass, ECM）的位置通常有0.8 mm的盲区[9]，因此，静态半径不可避免会存在误差。同时，其它相关因素也都会带来静态半径误差：加速度计有效质量中心与加速度计参考面的相对位置，测试中所有机械辅助构件的尺寸大小及其与加速度计有效质量中心的相对位置等。

静态半径误差的存在会导致加速度计正向输入和反向输入时，其真实的静态半径存在较大差异，从而引起正向标度因数和负向标度因数存在不对称性，并影响对线性系数的估值。如在高精度测试中，标称为1 m的转台半径，1 μm的误差会导致所施加的加速度产生 1×10-6的误差[9]。

基于离心机对加速度计进行测试标定的相关方法，在文献中都有相关规定[10-11]。目前确定静态真实半径或者补偿静态半径误差的方法是利用重力场翻滚设备测试标定出加速度计的标度因数，然后在离心机上的多种条件下在 0～1g取点（点数＞7）：离心机顺时针、逆时针，加速度计正向输入、反向输入等多种情况，然后利用加速度在不同转速下的输出及已知的标度因数，用平均法或者最小二乘法获取静态半径及其误差的估计值，当静态半径误差超出测试要求时，重新调整加速度计安装定位面的位置，直到误差满足要求。

基于上述方法可以获得静态半径及其误差的估计值，但测试点较多，工作量太大，实际中难以应用。本文针对上述问题，基于双离心机系统，提出一种静态半径的测试修正方法。该方法利用加速度计在双离心机上正向输入和反向输入条件下其安装位置误差的对称性，将安装位置误差项引入加速度计的静态模型方程中，通过方程的求解，可获取安装位置误差值，实现对静态半径的修正，同时在计算获取加速度计标度因数时，消除安装位置误差所带来的影响。

1 双离心机的工作原理

双离心机的机械台体由稳速台、随动台组成，如图1所示。其中，随动台（从离心机）安装在稳速台（主离心机）的转盘或者转臂上，且其回转轴与稳速台回转轴平行，通过稳速台和随动台同时旋转来产生正弦加速度信号。稳速台用来产生加速度信号的幅值，随动台用来实现加速度信号的频率和相位。

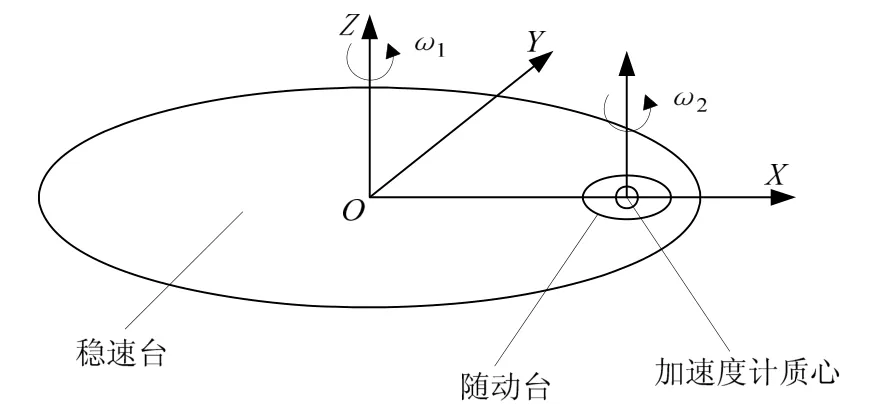
图1 双离心机工作原理示意图Fig.1 Sketch map of working principle for double centrifuge

作用在加速度计输入轴方向的加速度按式(1)计算[10-11]：

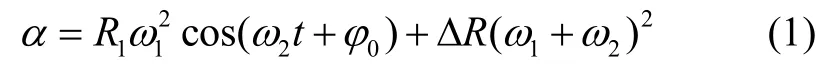
式中：a为被测加速度计输入轴方向的加速度，m/s2；ω1为稳速台角速度，rad/s；ω2为随动台角速度，rad/s；R1为稳速台静态半径，m；ΔR为随动台回转中心到加速度计的有效质量中心的距离，m；t为时间，s；0φ为加速度计的初始位置，rad。

如果不考虑加速度计安装时的位置误差，即ΔR=0，则式(1)可简化为：

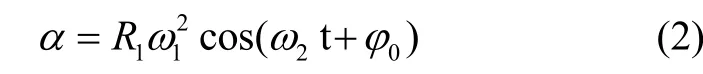
因此，作用在加速度计上的加速度峰值为：

2 静态半径误差项的建模及测试分析流程

为简化分析，结合随动台的定位功能，仅考虑加速度计敏感轴与稳速台的离心加速度同向或者异向的情况。加速度计在随动台上的安装误差示意图如图 2所示，结合图1，可知稳速台旋转中心O1与随动台旋转中心O2之间的距离为R1，稳速台旋转中心O1与加速度计的检测质量质心O3之间的距离为R3，且有ΔR=R1-R3。

在把加速度计安装固定到随动台面的过程中，理想状况下是使O3与O2重合，此时实际的静态半径就与转台系统预设的静态半径相等，因此在这种状况下转台转动时实际施加到加速度计上的离心加速度就与转台系统显示的输出加速度相同。

但在实际安装中，由于加速度计的有效质量中心位置盲区的存在，以及夹具等其它因素的影响，导致O3与O2无法完全重合，也就是说ΔR通常情况下都不会等于零。这就导致了转台系统显示的输出与实际施加在加速度计上的离心加速度并不相等，从而产生标定误差。

从图2还可以看出，ΔR的存在还会导致加速度计正向输入和反向输入时静态半径的不对称，从而引起加速度计正向标度因数和反向标度因数的不对称性，同时也会严重影响加速度计模型方程中偶次项系数的准确性。

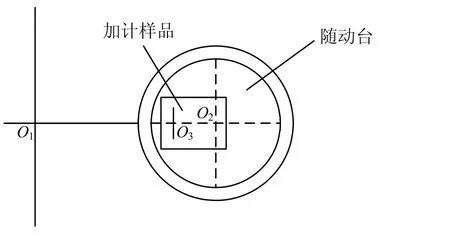
图2 加速度计在随动台上的安装误差示意图Fig.2 Sketch map of location error of accelerometer on sub-turntable

基于前面所述，可以建立静态半径误差项的分析模型，具体如下：

首先将加速度计通过夹具固定到随动台台面的定位固定孔，使随动台定位在0°时，加速度计敏感轴与转台离心加速度的方向相同，随动台定位在180°时，加速度计敏感轴与转台离心加速度方向相反。设稳速台的离心加速度为某一特定值a0，当随动台定位在0°时，对应的加速度计输出为U01，当随动台定位在180°时，对应的加速度计输出为U02。当an= a0+nΔa（n≥1，Δa为设定的离心加速度步进）时，则随动台在零位和180°时，加速度计对应的输出记为Un1和Un2。

由加速度计的一阶模型：

其中，Un为离心加速度为an时加速度计的输出。考虑ΔR的影响时，则当随动台定位在0°时，有：

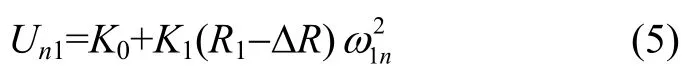
当随动台定位在180°时，有：

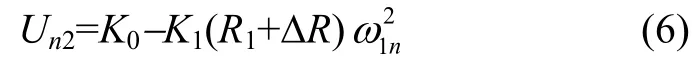
由式(5)(6)可得：

由式(7)可知，对应于任何一个an，由加速度计的两个输出值Un1和Un2，可求解获得一个不含有ΔR项的K1n，也就是说，这种测试计算方法消除了安装位置误差的影响。

当n≥2时，可采用取均值的方法降低测试过程中的偶然误差：

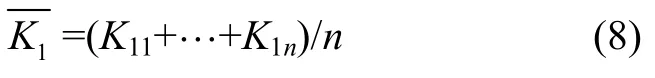
同时，基于式(5)～(8)可得：

或者

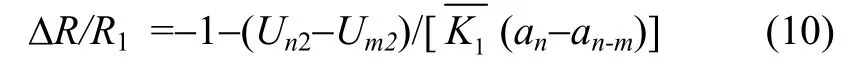
其中，m≠n。由式(9)和(10)，通过计算可获得多组（ΔR/R1）值，可根据实际需要确定所需计算的（ΔR/R1）的组数，最后通过对多组（ΔR/R1）值求均值，可获得关于（ΔR/R1）的一个测量值。该值表征了安装位置的误差，可以利用其对加速度计的性能指标校准值进行修正，从而提高对加速度计校准的精度，也可以利用最小二乘法获取K1及R/ΔR。

由式(7)，令

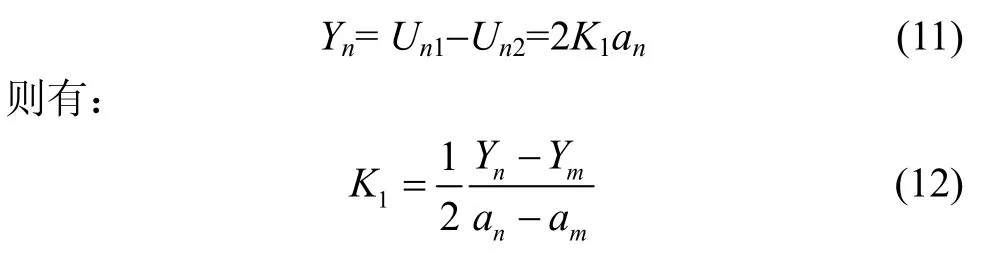
由以上可知，对应于任一输入an，都有一个Yn相对应。因此，采用最小二乘法对所有数据(an,Yn)进行线性拟合，则由拟合直线的斜率乘以0.5可得到K1的计算值。同样，上述过程也消除了ΔR的影响。同时，将式(12)所获得的K1代替式(9)和(10)中的K1均值，也可以获得ΔR/R1的值。

3 测试验证

测试验证中所采用的加速度计是 Silicon Designs公司的产品Model 1221-005，该加速度计的量程是±5g。

图3 加速度计及其测试夹具Fig.3 Accelerometer and mounting fixture

测试流程如下：

①对随动台进行上电、回零，使随动台定位于零位；

②通过安装夹具，将加速度计固定到随动台台面上并使加速度计敏感轴的方向与稳速台旋转时的离心加速度的方向相同；

③完成加速度计测试所需的电连接；

④设定线加速度模拟转台的输出加速度为某一特定值 1g，待输出的加速度稳定后，读取加速度计的输出读数U11；

⑤将线加速度模拟转台的输出加速度设定为2g、3g、4g和 5g，待输出加速度稳定后，分别记录下加速度计的输出读数Un1；

⑥使随动台旋转 180°，重复步骤④和⑤，对应于1g、…、5g，分别记录下加速度计的输出读数Un2；

⑦使用式(11)对测试数据进行处理，然后采用最小二乘法对所有数据进行线性拟合，获得不含安装位置误差的K1，并进一步根据修正后的K1值计算获得ΔR/R值。

上述过程中，通过转台的位置定位来实现正向输入和反向输入的转换，避免人为拆装所带来的安装误差项的变化。

测试验证的方案是，首先按照正常的安装步骤，调整夹具的固定位置，通过目测的方法尽量使加速度计的有效质量中心与随动台的回转中心在垂直方向上重合，也就是使O3与O2尽量靠近，然后按照上述测试流程完成第一次测试。

第二次测试中，利用夹具中的沟槽（如图3中的红色方框所示）重新调整夹具的位置，故意增大加速度计的有效质量中心与随动台的回转中心在垂直方向上的距离，也就是故意增大O3与O2之间的距离，然后按照上述测试流程完成第二次测试。

按照式(11)进行数据处理，然后采用最小二乘法对数据（an,Yn）进行线性拟合，获得K1。对比第一次测试和第二次测试所获得的K1，判断上述消除安装位置误差项的方法的有效性。基于所获得的K1，还可以分别获得两次测试中的安装误差项ΔR/R。

按照上述测试方案分别进行测试，所获得的数据及相关的数据处理结果如表1和表2所示。

对表1和表2的第一列和第四列分别进行线形拟合，可分别获得不含ΔR的K1，结果分别如图4和图5所示。

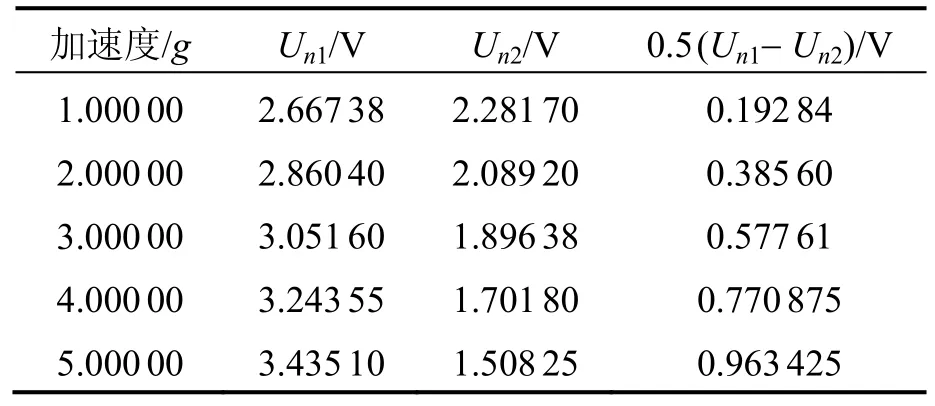
表1 正常安装条件下的加速度计测试数据Tab.1 Data from measurement under normally mounted condition

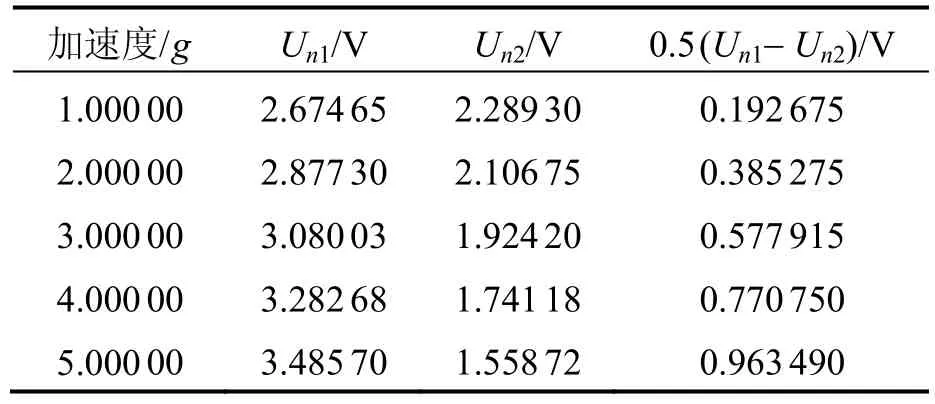
表2 增大安装位置误差后的加速度计测试数据Tab.2 Data from measurement after increasing the locaton error

以两次测试所获得的K1代替式(9)或(10)中的可分别获得两次测试中的安装位置误差：

第一次：︱ΔR/R1︱≈ 0.37%；

第二次：︱ΔR/R1︱≈ 5.22%。

参考图2的示意图，以O2为参考点，当O3比O2更接近稳速台回转中心时，ΔR/R1为正，当O3比O2远离稳速台回转中心时，ΔR/R1为负，此处只用绝对值讨论位置误差值的大小，不考虑其相对方向。同时，当ΔR/R1的绝对值较小时，如第一次测试时的情况，则测试过程中的随机波动对参数的影响较大，选用不同的m、n值时ΔR/R1的相对波动较大，此时常通过计算多个ΔR/R1值并求平均值的方式来处理。

由图4及图5的结果及ΔR/R1的计算结果可知，在两次测试过程中，虽然第二次测试中人为增大了安装位置误差，使两次测试中安装位置误差ΔR/R1相差大于10倍（0.37%和5.22%），但通过本文所提出的处理方法，有效消除了安装位置误差对标度因数的影响。最后所获得的标度因数，其波动小于 0.04%，验证了本方法的有效性。

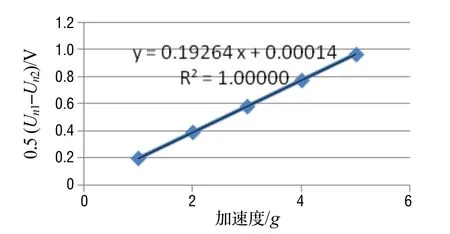
图4 第一次测试所获得的标度因数K1Fig.4 Scale factor from the first measurement

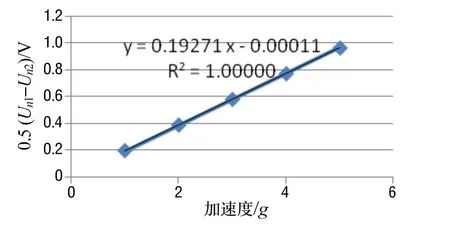
图5 第二次测试所获得的标度因数K1Fig.5 Scale factor from the second measurement

4 结 论

从实际工程应用的需求出发，针对加速度计在精密离心机上进行测试标定时，由于安装位置误差所引起的静态半径误差问题，提出一种消除双离心机静态半径误差的测试方法。该方法基于加速度计在双离心机上测试标定时在正向输入和反向输入条件下其安装位置误差的对称性，将安装位置误差项引入加速度计的静态模型方程中。通过对模型方程的处理，消除了结果数据中的安装误差项，获得了不含安装误差项的加速度计标度因数计算方法，并且基于所获得的标度因数，可以计算获得安装位置误差的估值。

最后，采用 Silicon Designs公司的产品 Model 1221-005对所提出的方法进行测试验证，证明了本方法的有效性。本方法有效简化基于双离心机的加速度计标定方法，大大降低了对加速度计安装的位置对准要求，并提高了测试标定精度。

参考文献（References）：

[1]Sohrabi H, Ebadollahi S. Accuracy enhancement of MEMS accelerometer by determining its nonlinear coefficients using centrifuge test[J]. Measurement, 2017, 112:29-37.

[2]Aydemir G A, Saranll A. Characterization and calibration of MEMS inertial sensors for state and parameter estimation applications[J]. Measurement, 2012, 45(5): 1210-1225.

[3]O’Loughlin C D, Gaudin C, Morton J P, et al. MEMS accelerometers formeasuring dynamic penetration events in geotechnical centrifuge tests[J]. International Journal of Physical Modelling in Geotechnics, 2014, 14(2): 31-39.

[4]Wang S M, Ren S Q. Calibration of cross quadratic term of gyro accelerometer on centrifuge and error analysis[J].Aerospace Science and Technology, 2015, 43: 30-36.

[5]Wang S M, Ren S Q. Calibration accuracy of error model coefficientsK2andK3of gyro accelerometer influenced by errors of centrifuge[J]. Nanotechnology and Precision Engineering, 2013, 11(2): 140-145.

[6]Xiao P, Liu L, Wang X B, et al. Non- linearity analysis of a capacitance detector diodes circuit for closed-loop micro-silicon accelerometer[C]//Proceedings of the 35th Chinese Control Conference. Chengdu, China, 2016.

[7]Guan W, Meng X F, Dong X M. Testing transverse sensitivity of linear single-axis pendulous accelerometer with double turntable centrifuge[J]. MAPAN-Journal of Metrology Society of India, 2016, 31(1): 69-74.

[8] 廖建平, 尹晓丽, 李晓婷. 加速度计的离心加速度场翻滚校准方法[J]. 中国惯性技术学报, 2017, 25(4): 550-560.Liao J P, Yin X L, Li X T. Tumbling calibration method for accelerometer in centrifugal acceleration field[J]. Journal of Chinese Inertial Technology, 2017, 25(4): 550-560.

[9]IEEE Std 836TM-2009. IEEE recommended practice for precision centrifuge testing of linear accelerometers[S].

[10]JJF 1426-2013. 双离心机法线加速度计动态特性校准规范[S]. 北京: 国家质量监督检验检疫总局, 2013.JJF 1426-2013. Calibration specification for dynamic parameters of linear accelerometer used double centrifuge[S].Beijing: China’s General Administration of Quality Supervision, Inspection and Quarantine, 2013.

[11]JJF 1427-2013. 微机电（MEMS）线加速度计校准规范[S]. 北京: 中华人民共和国国家质量监督检验检疫总局, 2013.JJF 1427-2013. Calibration specification for MEMS linear accelerometers[S]. Beijing: China’s General Administration of Quality Supervision, Inspection and Quarantine, 2013.