航天器有限时间自适应容错姿态控制

胡 建，白瑜亮，王小刚，耿云海，崔乃刚

（哈尔滨工业大学 航天学院，哈尔滨 150001）

高精度姿态控制是航天器系统的重要关键技术之一，在对地定向与观测、交会对接、航天器编队飞行等多种空间任务中起到十分重要的作用。近年来，随着航天器技术的发展，出现了多种低成本、模块化、可快速发射的新型航天器，如美国的TacSat系列卫星和ORS Sat-1等；同时，各国正在争相发展结构和功能均比较简单的微小型航天器。这些新型航天器质量轻，结构简单，具有较少的冗余和备份，一旦姿态控制执行器发生故障或部分失效，将会对航天器的姿态控制性能造成很大影响，甚至导致任务失败。此外，这些航天器大多在中低轨道运行，受到气动干扰力矩的影响大，加之由于安装偏差、燃料消耗、帆板展开等造成的系统参数不确定性，造成姿态控制器精度降低。因此，为保证航天器任务的顺利实施，设计具有容错能力并能够克服系统不确定性的高精度姿态控制方法是十分必要的。

针对上述问题，基于自适应控制方法的姿态控制器因其良好的性能受到很多学者的关注。自适应控制根据实际情况自动调整控制参数，能够保证系统存在参数、结构、环境参数等不确定性时仍然能够得到期望的控制效果。文献[1]和文献[2]利用自适应控制理论对存在执行器故障条件下的航天器姿态控制问题进行研究，分别设计了四元数反馈自适应容错姿态控制器[1]和基于输入状态稳定性的自适应姿态控制器[2]。自适应控制还可与滑模控制[3-4]、鲁棒控制[5-6]、自抗扰控制[7]、神经网络[8]、反步控制[9-10]等方法相结合，通过对系统不确定性或不确定性上界进行估计，设计了考虑系统不确定性补偿的新型自适应姿态控制器。在考虑系统外部干扰的基础上，文献[8]和文献[11]利用双曲正切函数设计了考虑执行机构饱和特性的有限时间姿态控制器，而文献[5]则重点考虑了未知的飞轮摩擦力矩的影响。文献[12]和文献[3]对角速度不可测时的航天器姿态控制问题进行研究。文献[12]提出了由修正的Rodrigues参数描述的单航天器输出反馈姿态控制方法和多航天器分布式输出反馈姿态控制器；文献[3]提出一种自适应有限时间状态观测器对姿态四元数时间变化率进行估计，仅需姿态角信息即可进行航天器姿态控制。针对航天器姿态控制中可能存在的执行器故障、外部扰动力矩、系统不确定性等问题，现有方法大多只考虑了其中某一因素的影响，所设计的姿态控制器存在普适性差的缺点。此外，现有方法对执行器的能力约束考虑较少，不少控制方法在初始阶段产生的需求控制力矩远远超出执行器的能力范围，这在实际中是无法实现的。

本文将自适应控制与滑模控制理论相结合，并考虑系统的有限时间稳定性，提出一种新型的有限时间自适应容错姿态控制方法。首先，基于四元数建立了航天器姿态数学模型，考虑执行器故障及饱和特性，以及航天器转动惯量偏差、外部干扰力矩等系统不确定性。然后，设计一种自适应参数更新方法，对系统不确定性上界进行估计，并在利用滑模和有限时间理论进行姿态控制器设计时对其进行补偿，保证系统的容错能力和鲁棒性。该控制方法不仅能保证系统的渐进稳定性，而且是有限时间稳定的，文中利用Lyapunov稳定性理论进行了证明。最后，通过数值仿真验证了所提出控制方法的有效性。

1 航天器姿态数学模型

采用姿态四元数建立航天器姿态运动学模型：

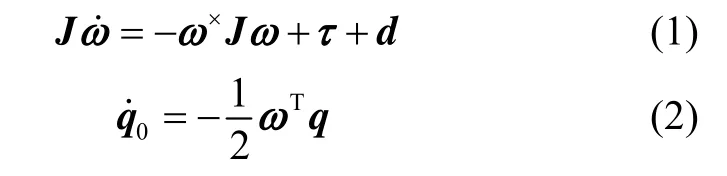
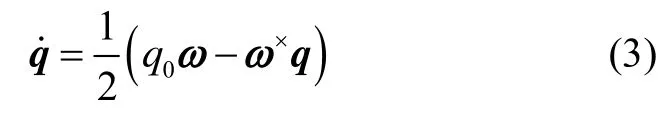
其中：J是航天器转动惯量矩阵；是航天器相对于惯性系的姿态角速度在本体系下的投影；是作用于航天器本体的控制力矩；是航天器受到的干扰力矩；是航天器本体系和惯性系间的姿态四元数，满足

×ω为反对称矩阵，表示为

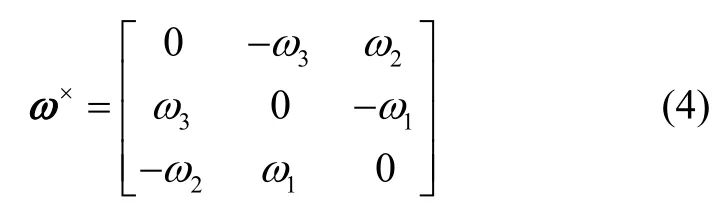
根据上述关系，得到航天器姿态跟踪误差模型为

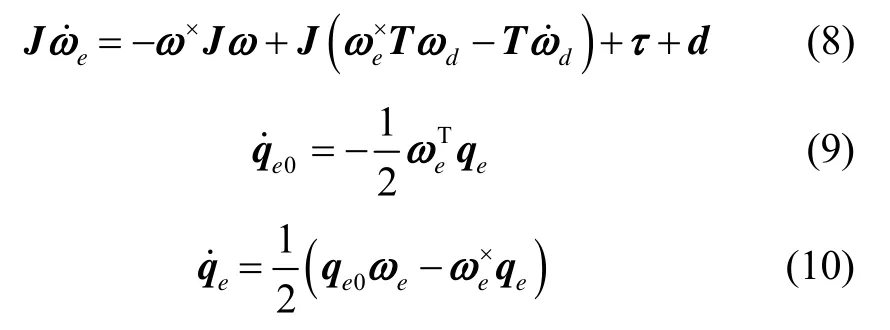
在航天器姿态控制系统实际应用中，由于安装误差等原因，航天器转动惯量矩阵存在不确定性，可写为其中J0为标称值，ΔJ为不确定量。此外，当执行器饱和或产生故障时，无法有效实现控制输入信号，这将严重影响航天器的姿态控制性能。

考虑航天器执行器故障，主要包括乘性故障和加性故障，建立航天器执行器的故障模型：

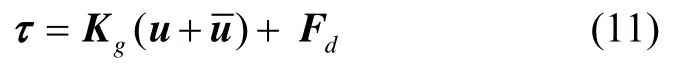
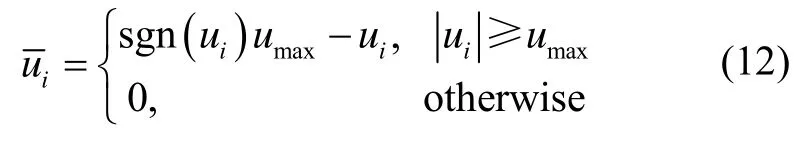
考虑航天器转动惯量矩阵偏差和执行器故障，航天器姿态跟踪误差模型可表示为

本文进行航天器姿态控制系统设计时，在全局范围内进行以下假设。

假设 1 航天器转动惯量矩阵J是正定对称的，且满足

其中，Jmax为正常数，表示向量的2范数。

假设 2 控制过程中，外部干扰d有界，满足执行器参数Fd和有界，满足其中为未知上界且均为正常数。

本文的主要目的可概括为：在考虑执行器故障、航天器转动惯量不确定、干扰力矩等条件下，设计有限时间自适应容错姿态控制器，实现姿态误差系统在有限时间内的全局渐进稳定。

2 有限时间自适应容错控制器设计

（i）V(t)为正定函数；

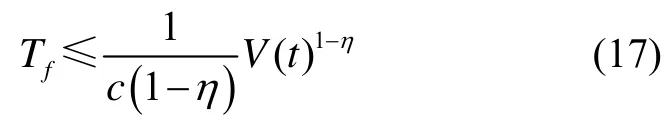
本文将滑模面选取为：

将式(19)中不含不确定项的标称表达式用N(t)表示，将所有不确定项用Δ(t)表示。

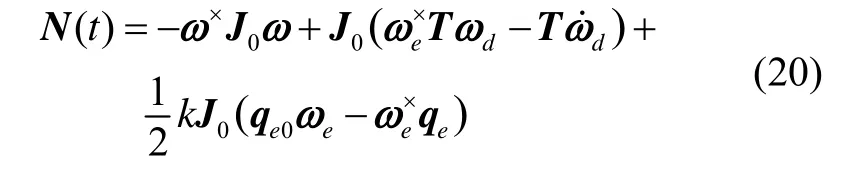
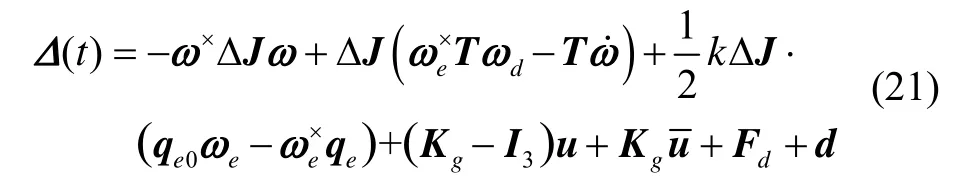
于是，航天器的姿态跟踪系统模型表示为

假设3 根据假设1和假设2，式(21)表示的系统总的不确定性Δ(t)有界，且满足其中为未知上界且均为正常数。

引理 1 考虑式(18)中的滑模面，如果任意s(t)满足则式(10)和(13)满足和

根据上述模型和假设，给出考虑系统不确定性条件下的自适应容错姿态控制律：

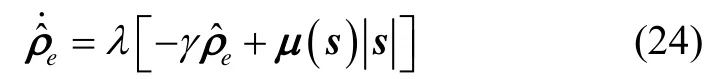
其中，ε为小量正常数。

定理1 考虑式(8)～(10)中的航天器姿态跟踪模型和式(18)中的滑模面，利用式(23)给出的姿态控制器和式(24)中的自适应变量更新，可使误差姿态四元数qe和误差姿态角速度eω在有限时间内收敛至0的小邻域。

证明：定义如下Lyapunov函数：

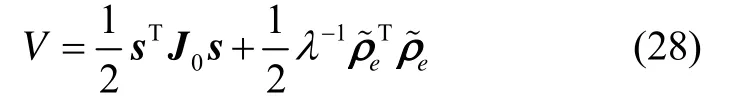
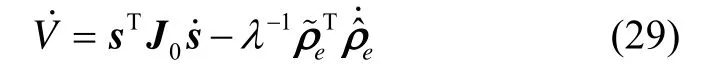
根据式(22)～(24)，式(29)整理成：

根据式(16)，式(30)右边第一项满足：

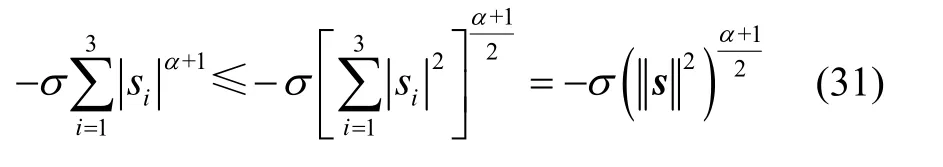
考虑假设1，可得：

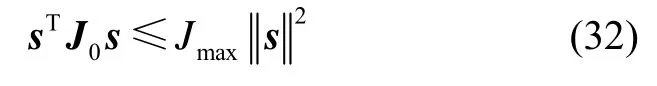
将式(31)(32)代入式(30)得：

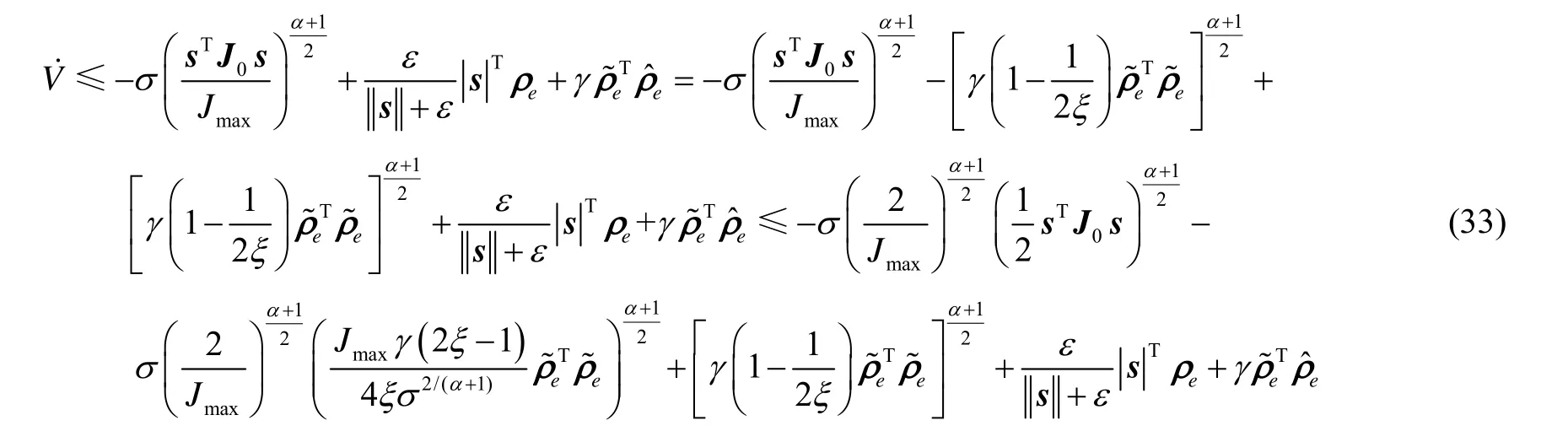
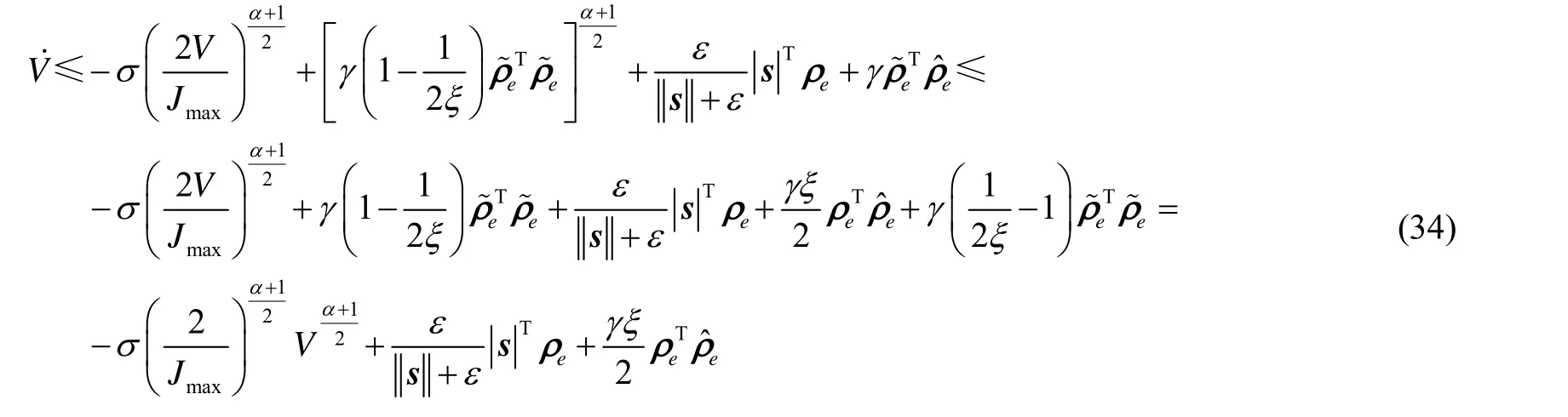
写为

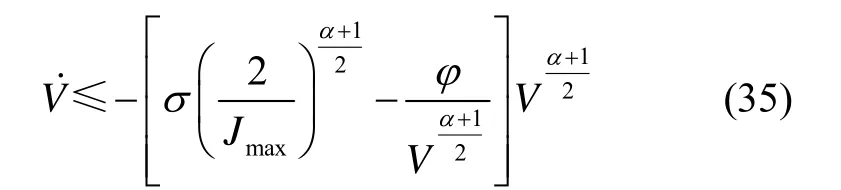
根据有限时间稳定定理，当

成立，则 Lyapunov函数V在有限时间内收敛到零附近，收敛精度满足

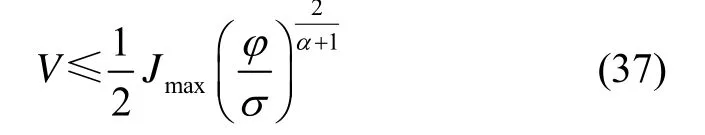
收敛时间满足

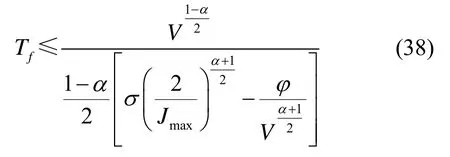
证毕。

本节针对存在系统不确定性和外部扰动的姿态跟踪模型，设计了自适应容错姿态控制器。基于系统不确定性有界条件设计了自适应控制变量，保证系统在有限时间的稳定性。为消除抖振，用饱和函数代替符号函数，即将式(25)中的替换成：

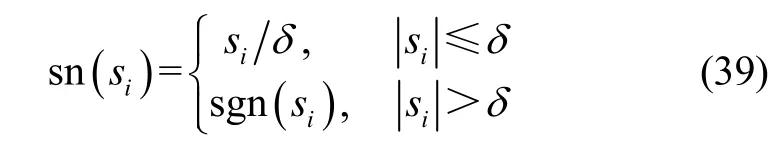
其中，δ是正常值小量。

3 仿真分析

为验证所设计的有限时间自适应容错姿态控制器的有效性，本节进行数值仿真。将所设计的控制器性能与经典PD姿态控制器进行对比，PD姿态控制器如下：

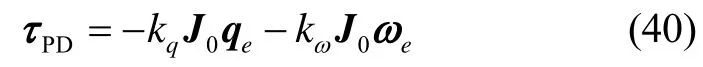
航天器转动惯量标称值J0和偏差值ΔJ分别为：

执行器故障参数如下：

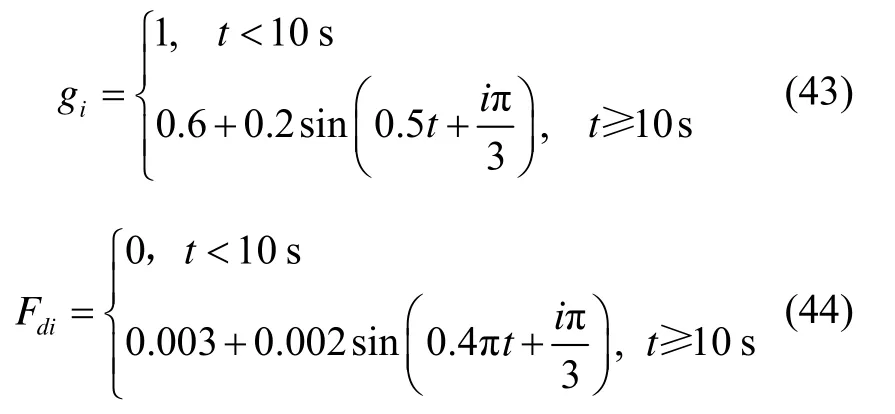
外部干扰力矩如下：

航天器的初始姿态四元数和角速度为：

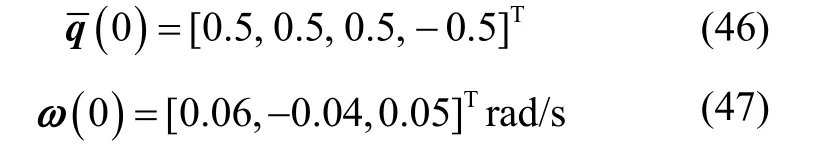
期望姿态为

为了验证控制方法的鲁棒性，采用PD控制律结合无干扰的航天器动力学模型产生期望轨迹。然后，对比分析有限时间自适应容错控制器和PD控制器在存在扰动和执行器故障条件下的姿态跟踪精度。

有限时间自适应容错姿态控制器参数取为：

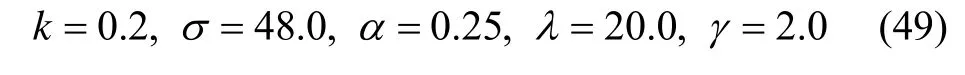
式(40)中PD姿态控制器参数取为：

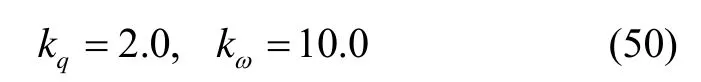
图1 姿态四元数Fig.1 Quaternion

采用式(23)中的有限时间自适应容错姿态控制器得到的姿态控制结果如图1～2所示。图1为航天器姿态四元数曲线，图2为姿态角速度曲线。由图1～2可知，本文提出的有限时间自适应容错姿态控制方法能够实现存在执行器故障和干扰条件下的高精度姿态稳定跟踪控制。图3为航天器姿态控制力矩曲线；图4为滑模面变化曲线，滑模面收敛精度可达10-6量级。图5和图6为有限时间自适应容错姿态控制器作用下的姿态四元数跟踪偏差与经典 PD姿态控制器的对比。利用所提出的有限时间自适应容错姿态控制方法，航天器的姿态跟踪误差可控制在10-4rad量级，满足高精度姿态控制的要求。传统 PD控制器虽然也能实现对期望姿态的稳定跟踪，但姿态跟踪精度远低于本文提出的有限时间自适应容错姿态控制方法。仿真结果充分说明了本文提出的方法具备在存在执行器故障和系统不确定条件下实现高精度姿态控制的良好性能。

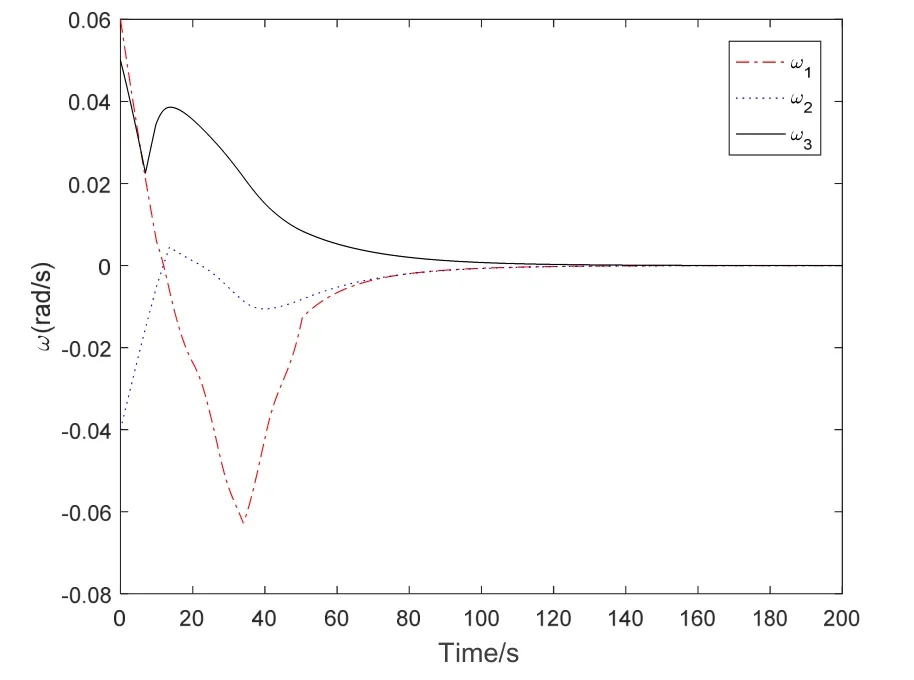
图2 姿态角速度Fig.2 Angular velocity

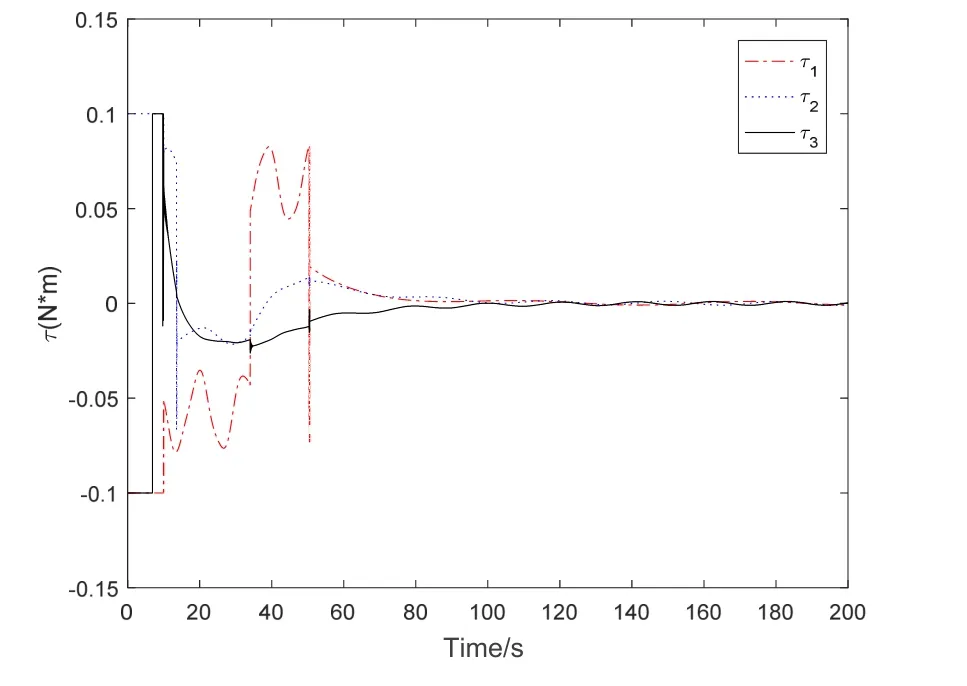
图3 姿态控制力矩Fig.3 Control torque of proposed control

图4 滑模面Fig.4 Sliding mode value

图5 姿态四元数 q 0 、 q1跟踪偏差对比Fig.5 Quaternionq0andq1tracking error comparison

图6 姿态四元数 q 2 、 q3跟踪偏差对比Fig.6 Quaternionq2andq3tracking error comparison

4 结 论

本文针对航天器存在执行器故障、转动惯量偏差及外部扰动等不确定性条件下的姿态跟踪问题，利用滑模控制理论和有限时间控制思想，设计了一种有限时间自适应容错姿态控制器，可以使航天器在有限时间内实现高精度姿态跟踪控制。通过合理地设计自适应变量实现对系统不确定性上界的估计和补偿，确保了控制器在系统不确定条件下仍然具有较高的精度。本文利用 Lyapunov稳定性理论证明了所提出控制方法的收敛性和稳定性。数值仿真进一步验证了该方法的有效性和精度。

参考文献（References）：

[1]Han Y, Biggs J, Cui N G. Adaptive fault-tolerant control of spacecraft attitude dynamics with actuator failures[J].Journal of Guidance, Control, and Dynamics, 2015, 38(10): 2033-2042.

[2]Hu Q L, Xiao B, Wang D W, et al. Attitude control of spacecraft with actuator uncertainty[J]. Journal of Guidance,Control, and Dynamics, 2013, 36(6): 1771-1776.

[3]Shao S K, Zong Q, Tian B L, et al. Finite-time sliding mode attitude control for rigid spacecraft without angular velocity measurement[J]. Journal of the Franklin Institute,2017.

[4]宋申民, 郭永, 李学辉. 航天器姿态跟踪有限时间饱和控制[J]. 控制与决策, 2015, 30(11): 2004-2008.Song S M, Guo Y, Li X H. Finite-time attitude tracking control for spacecraft with input saturation[J]. Control and Decision, 2015, 30(11): 2004-2008.

[5]Cao X B, Wu B L. Indirect adaptive control for attitude tracking of spacecraft with unknown reaction wheel friction[J]. Aerospace Science and Technology, 2015, 47:493-500.

[6]陈海涛, 宋申民, 李学辉. 航天器有限时间饱和姿态跟踪控制[J]. 中国惯性技术学报, 2017, 25(4): 536-543.Chen H T, Song S M, Li X H. Finite-time saturated attitude tracking control for rigid spacecraft[J]. Journal of Chinese Inertial Technology, 2017, 25(4): 536-543.

[7]Bai Y L, Biggs J. A singular adaptive attitude control with active disturbance rejection[J]. European Journal Control,2017, 35: 50-56.

[8]Li M X, Hou M S, Yin C W. Adaptive attitude stability control design for spacecraft under physical limitations[J].Journal of Guidance, Control, and Dynamics, 2016, 39(9):2176-2180.

[9]方星, 吴爱国, 董娜. 阵风干扰下无人直升机轨迹的自适应反步控制[J]. 中国惯性技术学报, 2015, 23(1):59-65.Fang X, Wu A G, Dong N. Adaptive back stepping-base trajectory control of an unmanned helicopter in presence of wind gusts[J]. Journal of Chinese Inertial Technology,2015, 23(1): 59-65.

[10]Huo B Y, Xia Y Q, Yin L J, Fu M Y. Fuzzy adaptive fault-tolerant output feedback attitude-tracking control of rigid spacecraft[J]. IEEE Transactions on Systems, Man,and Cybernetics: Systems, 2017, 47(8): 1898-1908.

[11]李学辉, 宋申民, 陈海涛, 等. 航天器终端接近的有限时间输入饱和避碰控制[J]. 中国惯性技术学报, 2017,25(4): 530-535.Li X H, Song S M, Chen H T, et al. Finite-time and collision avoidance control for spacecraft terminal approach with input saturation[J]. Journal of Chinese Inertial Technology, 2017, 25(4): 530-535.

[12]高岱, 吕建婷, 王本利. 航天器有限时间输出反馈姿态控制[J]. 航空学报, 2012, 33(11): 2074-2081.Gao D, Lv J T, Wang B L. Finite-time output feedback attitude control of spacecraft[J]. Acta Aeronautica et Astronautica Sinica, 2012, 33(11): 2074-2081.