基于扩展卡尔曼滤波的转速补偿滚转角测量算法

王佳伟，祁克玉，杨恺华，梁 轲，闫 杰

（1. 西北工业大学 航天学院，西安 710072；2. 机电动态控制重点实验室，西安 710065）

面对现代战场武器装备高精度和低效费比的双重迫切需求，常规火炮不仅要延续其广阔区域火力压制的优势，还应具备在复杂环境中对小面积、低成本目标的精确打击能力。二维弹道修正引信正是一种实现低成本精确打击的前沿技术，通过更换弹道修正引信即可满足常规无控弹药智能化、灵巧化改造的迫切需求，是目前国际引信装备领域最炙手可热的发展方向。

基于中大口径迫/榴弹应用平台，采用惯性器件/卫星定位组合测量弹体姿态及弹道参数，将修正引信与弹体通过解耦部件连接构成双旋稳定弹（Dual-Spin Stabilized Projectiles），其修正原理如图1所示。

在气动力的作用下，修正引信头部的两对翼面分别产生滚转力矩和修正弹道所需控制力，这是目前国际上二维弹道修正引信技术中最具代表性的总体设计方案[1-2]。修正引信的实时滚转角直接影响修正方向，是弹道控制模块的重要输入信息，其准确测量是二维弹道修正技术有待解决的关键技术。陀螺/卫星定位组合测量方案作为滚转角测量的一种主流方法，最早于1995年由David J. Lucia提出[3]。近年多有文献进行进一步的阐述，其中HeeYoung Park等人继承并改良了David J. Lucia的算法[4-9]，但这些方法都是在修正引信不大于3 r/s的微旋状态且转速恒定的假设条件下提出的。在实际弹道环境中，修正引信转速从起控至修正末段的跨度可达数十转/秒，远远大于文献[4-9]所设定的理想情况，因此需要设计一种能够适应较大转速变化范围的滚转角测量方法以适应实际工程需求。

针对二维弹道修正引信全弹道转速变化范围较大的旋转特点，本文建立了修正引信滚转角与弹载陀螺/卫星定位输出的解析模型，将实测修正引信转速作为补偿引入系统量测方程，提出了一种基于扩展卡尔曼滤波（extended Kalman filter, EKF）的转速补偿滚转角测量算法。

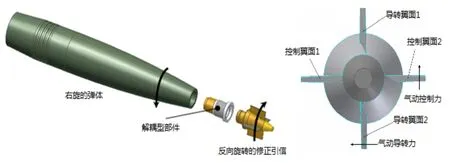
图1 二维弹道修正原理图Fig.1 Schematic of 2-D course correction

1 研究基础

1.1 二维弹道修正原理

二维弹道修正引信通过解耦部件与弹丸主体连接，可以自由旋转。引信头部安装四个斜置固定翼面，其中三个翼面带有左向斜置角，另外一个翼面带有右向斜置角。弹丸在飞行过程中，由于四个翼面均存在斜置角，都会产生一定的升力作用，其中：控制翼面1和2斜置角相反，其受到的气动力方向相同，这两个力对修正引信滚转方向的力矩相互抵消，仅形成向上的气动合力，即为弹道修正所需的控制力；导转翼面1和2斜置角相同，受到的气动力方向相反，力的作用相互抵消，却形成促使修正引信旋转的导转力矩，其方向与弹丸自转方向相反。当弹载控制器发出控制指令驱动滚转执行机构，使得修正翼面滚转角度指向期望方向时，其产生的气动升力即可改变弹丸原飞行轨迹，达到弹道修正的目的[10-11]。其原理如图1所示。

1.2 扩展卡尔曼滤波

卡尔曼滤波器是针对观测状态变量的最优线性滤波器，但对于复杂的非线性系统则需要用到一种非线性滤波方法，而EKF无疑是过去数十年应用最为广泛的非线性状态估计方法。

设k时刻带有离散量测的连续时间系统如下所示：

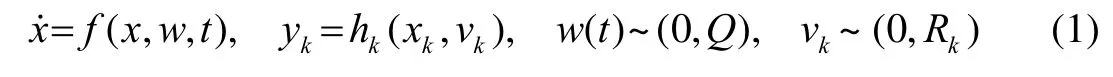
其中，x为被估计的状态变量，w为协方差为Q的系统噪声，v为协方差为Rk的量测噪声。如果记为状态变量的估计值，则可得到系统偏微分矩阵在当前状态估计的值为

此时状态估计误差的协方差Pk和传播协方差表达式如下：

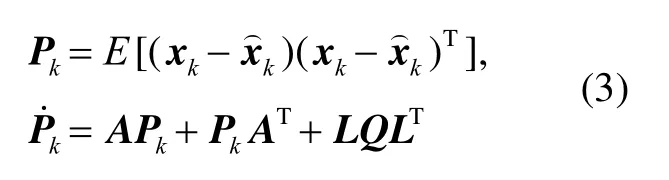
其中，A和L由式(2)给出。式(3)的积分方程将状态变量的估计和估计误差的协方差Pk由k-1时刻的后验估计状态传播到k时刻的先验估计状态，随后在每一个量测时刻按照离散卡尔曼滤波方程更新状态估计和协方差，如式(4)所示：

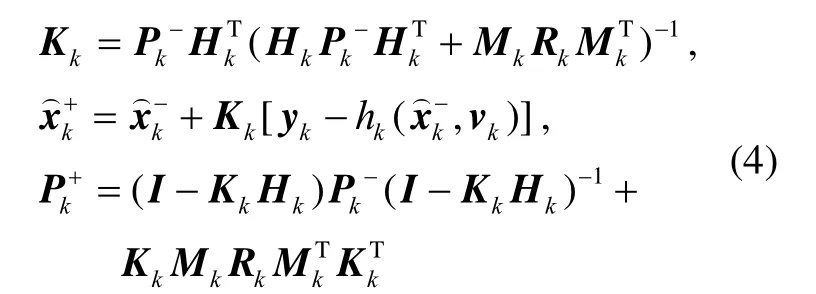
至此得到k时刻的后验状态变量估计，滤波方程的第k步计算结束。

1.3 陀螺/卫星定位组合算法

陀螺/卫星定位组合解算滚转角是利用卫星定位接收机实时测量弹丸在发射坐标系下三个方向的速度分量，考虑到弹丸攻角通常很小可以省略，可以通过速度估算得到准弹体系下修正引信此刻的俯仰角速度˙和偏航角速度˙。结合弹体坐标系下固连于修正引信内部的陀螺三个方向角速率输出根据外弹道学相关理论，利用坐标变换建立弹体坐标系下陀螺角速率输出与准弹体坐标系下俯仰/偏航角速率的物理解析关系，并从中解算得到滚转角γ。算法详见文献[4]，原理框图如图2所示。

遗憾的是，该方法仅局限于不大于 3 r/s的微旋恒定转速条件下的滚转角测量，基于理论解析得到的滚转角又极易受到量测噪声的影响，因此需要设计一种滤波算法以实现转速大范围变化环境下的滚转角准确测量。

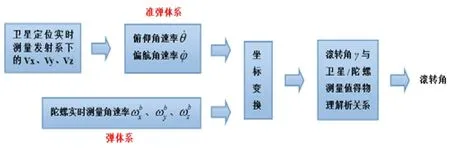
图2 陀螺/卫星定位组合测量滚转角算法原理Fig.2 Principle of roll estimation algorithm

2 滤波算法设计

以高速且时变转速旋转的修正引信会令传统EKF方法中每一次滤波迭代周期内滚转角增量突变，导致状态变量在滤波状态更新过程中发散，最终使滚转角估计误差逐渐增大。与传统的EKF方法不同的是，转速补偿 EKF滚转角测量方法在系统偏微分矩阵中增加了修正引信转速信息，经过积分得到单次迭代周期Δt内的滚转角增量Δγ，使其作为量测预估值kk H x的补偿能够最大限度地保证滤波算法迭代过程中滚转角的预估值收敛。

待估状态向量Xk包括转速p、初始滚转角γ0以及y、z轴陀螺测量误差，则：

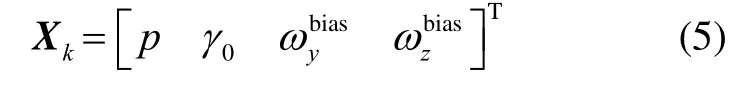
量测向量Zk为：

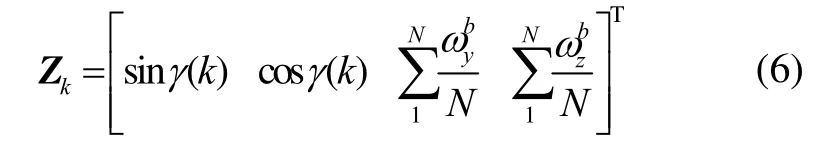
系统偏微分矩阵如式(7)～(10)所示：

3 仿真验证

3.1 仿真条件

某型双旋稳定迫弹射角采用最大射程角，弹丸初速为名义初速，在炮兵标准气象条件下全弹道弹丸稳定飞行，外弹道曲线见图3。

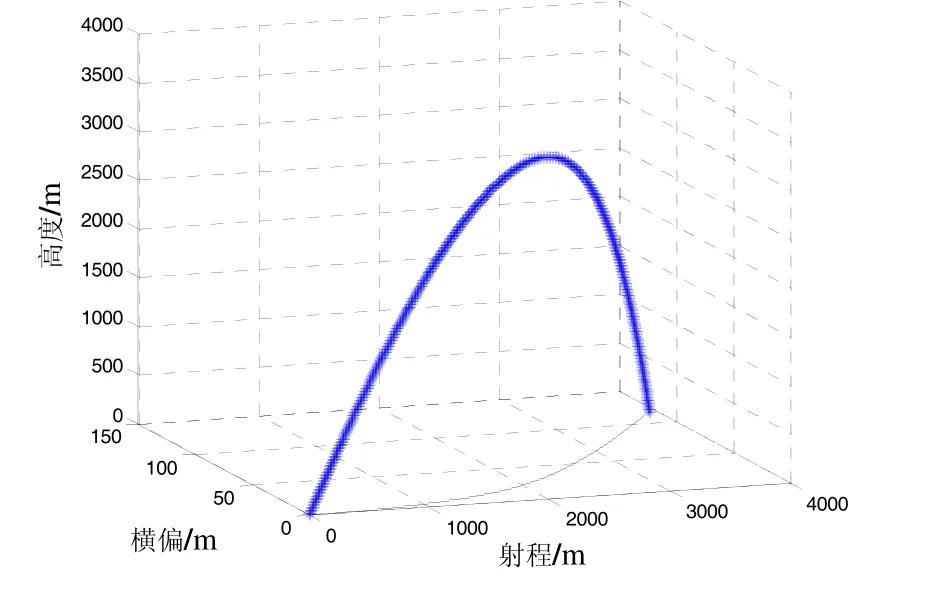
图3 双旋迫弹外弹道曲线Fig.3 Exterior trajectory curve of dual-spin mortar shell

图 4是全弹道范围弹丸和修正引信无控飞行的转速变化曲线。弹丸发射后，迫弹尾翼产生导转力矩使弹丸转速由静止状态迅速提升至11 r/s左右，之后转速随动压变化（由弹丸速度决定）呈倒“U”型变化趋势且全弹道保持右旋（从弹尾向弹头方向看去）。修正引信头部安装了与弹丸尾翼反向的导转翼面，在反向导转力矩作用下转速迅速提升至25 r/s左右，随后在导转力矩、摩擦力矩和滚转阻尼力矩的合作用下自由旋转，使其在全弹道内与弹丸旋转方向相反，即向左旋转。

图4 弹丸和引信全弹道转速变化曲线Fig.4 Rotation speed curves of shell and fuze

假设北斗卫星定位接收机在 10 s内实现重捕定位，由图4可以看到整个修正阶段的引信转速将在15 r/s至25 r/s之间波动，远远超过文献[5-6]算法中微旋且恒定的转速限制，因此需要一种既能满足修正控制初期较高转速条件，又能不失精度地满足起控后微旋状态下的修正引信滚转角测量方法。表1给出了应用于滚转角测量模型中的各测量参数。

表1 测量模型参数Tab.1 Parameters used in simulation

3.2 高转速验证

在3.1节所述仿真条件下，采用理论解析方法解算得到的滚转角误差，如图5所示。可以看到滚转角真值完全湮没在噪声中无法分辨，其误差分布呈现出弹道中段较小而弹道初段及末段较大的趋势，这是因为修正引信的转速恰好在弹道中段最低，其带来的一个仿真步长周期内的滚转角累积误差也最小。这也侧面印证了理论解析方法对于较高转速条件下的滚转角测量是完全失效的。

采用引入转速补偿的 EKF算法对修正引信滚转角进行优化估计，图6为使用滤波算法前后的滚转角解算误差对比，图7为10 s后的解算误差局部放大图。

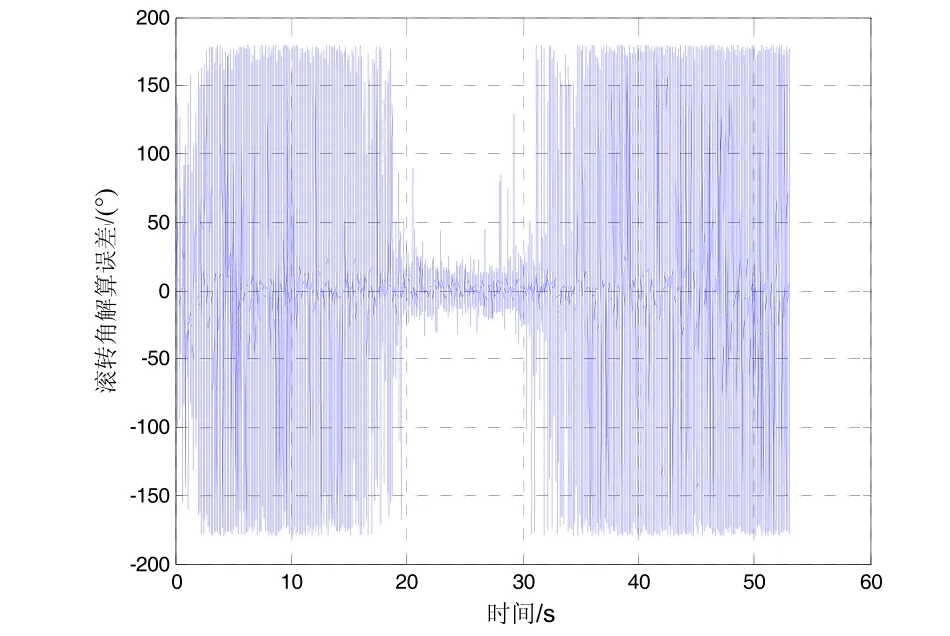
图5 高转速条件下理论解析法滚转角解算误差Fig.5 Roll estimation error by theoretical analytical method in the case of high rotation speed

可以看到采用引入转速补偿 EKF滤波算法的滚转角估计值与真值之间的误差迅速收敛，收敛后全弹道滚转角解算绝对误差不超过5°，经统计误差均值为-1.66°，方差为1.84°。宏观来看，滚转角解算误差在弹道初段及末段有所增大，这是由于该时间段修正引信转速较大而导致每一个仿真步长内滚转角增量过大，预测协方差和滤波器的增益不能随新息同步改变从而失去对突变状态变量的跟踪能力，使估计误差略有增加。以图4为例，修正引信的转速在弹道初段及末段超过了15 r/s，这意味着仅在一个步长周期内预估状态变量的增量就有 5.4°，因此采用转速补偿的 EKF算法对修正引信滚转角的估计效果是令人满意的。

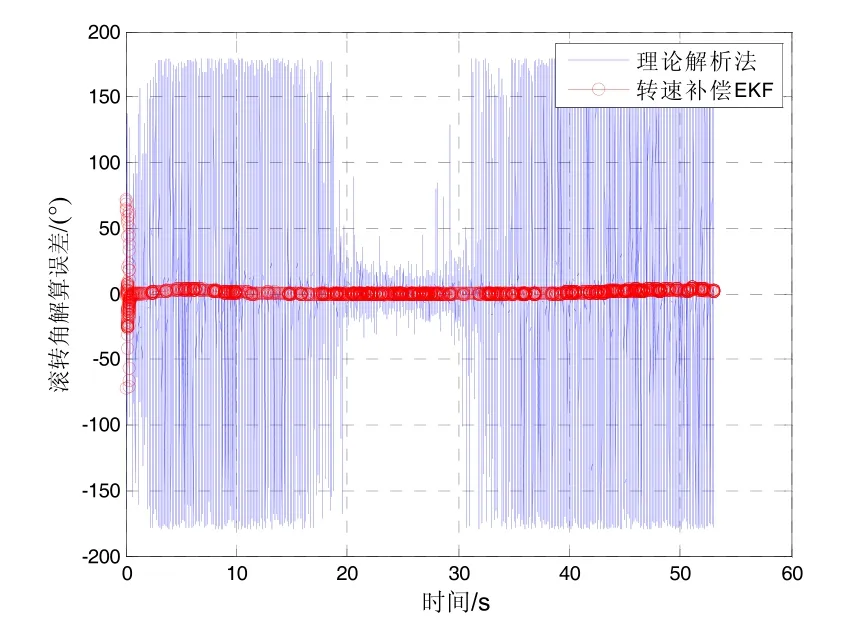
图6 滤波前后的滚转角解算误差对比Fig.6 Comparison of roll estimation error with theoretical analytical method and EKF

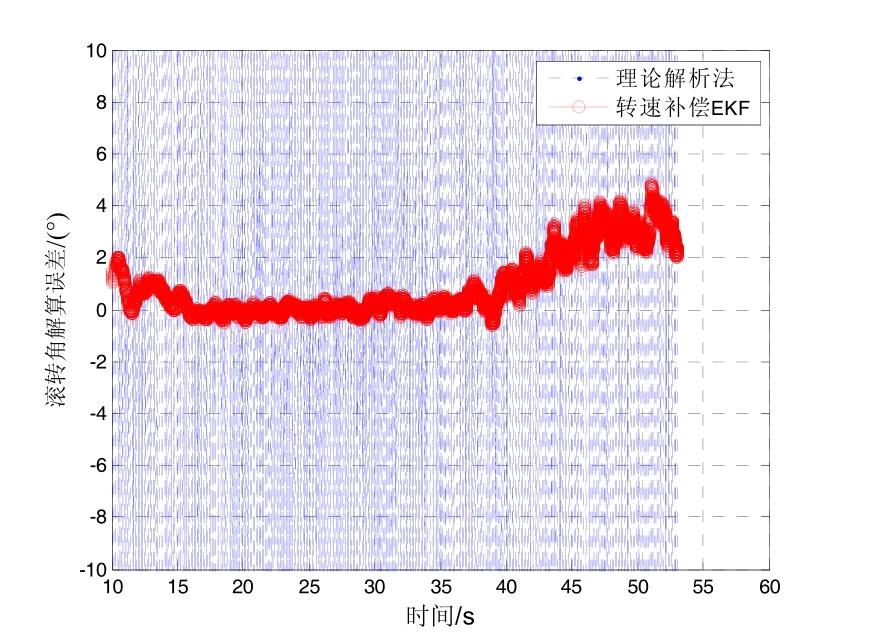
图7 误差对比局部放大图Fig.7 Magnification of roll estimation error

3.3 低转速验证

针对起控后弹道修正阶段的低转速环境，转速补偿的EKF算法同样需要准确测量实时滚转角。为了足够真实地模拟修正引信较低转速环境，而又不改变其在弹道飞行过程中所受升力和阻力等气动条件，仅将弹道模型中修正引信的滚转阻尼力矩系数增大，令其转速降低至1～5 r/s。引入转速补偿的EKF滚转角测量结果如图8所示。

可以看到，引入转速补偿的EKF算法在低转速条件下滚转角测量精度依然表现出色，解算误差迅速收敛且全弹道绝对误差不大于 2.5°，经统计解算误差在收敛后的误差均值为-0.34°，方差为0.35°。由此可见，转速补偿后的 EKF滚转角测量算法有别于传统理论解析方法，对于高速、低速且时变转速条件下的滚转角测量都具有很好的解算效果。

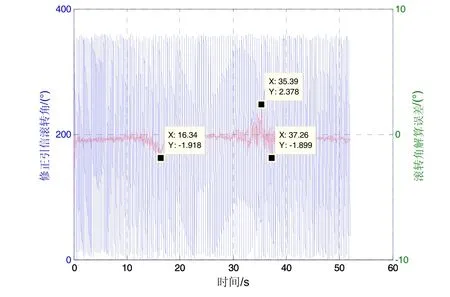
图8 1～5 Hz转速条件下滚转角解算误差Fig.8 Roll estimation error under low spinning rate

4 实验验证

以高精度MEMS传感器三轴转台作为实验平台，验证转速补偿EKF滚转角测量算法，如图9所示。

通过滚转控制单元设置由30 r/s均匀减小至1 r/s的滚转速率，固连在滚转轴上的滚转角测量硬件模块会采集陀螺输出信号，最后将采用转速补偿EKF滚转角测量算法计算出的实时滚转角与理论值进行对比，分析解算误差。三轴转台滚转角速率输出以及对应角速率条件下滚转角解算误差曲线如图10所示。

由图10可以看到，在修正引信转速自30 r/s至1 r/s范围动态变化过程中，除了滤波迭代初期的振荡之外，仅有的滚转角解算失准皆是出现在转速状态突变所对应时刻（其收敛过程都不会超过 200ms），但转速补偿EKF滚转角测量算法始终能够保持较高的测量精度，且滚转角解算绝对误差不超过 4°。由此可见该算法完全能够实现大范围转速变化条件下的滚转角准确测量。

图9 MEMS三轴转台Fig.9 MEMS three-axis turntable

图10 实验室验证滚转角解算误差曲线Fig.10 In-lab testing results with three-axis turntable

5 结 论

本文通过双旋稳定迫弹的外弹道模型分析了修正引信转速在全弹道大范围变化的转动特性，提出了一种基于扩展卡尔曼滤波的转速补偿滚转角测量方法。验证结果为：1）在较高转速仿真条件下，采用该估计方法500 ms内就可以实现滚转角解算快速收敛，全弹道滚转角解算绝对误差不大于5°，误差均值为-1.66°，方差为1.84°；2）在低转速仿真条件下，滚转角解算误差仍可迅速收敛且全弹道绝对误差不大于 2.5°，收敛后的误差均值为-0.34°，方差为0.35°；3）以三轴转台为实验平台进行验证，该算法滚转角解算绝对误差不超过4°。以上验证结果表明该算法完全可以满足二维弹道修正引信系统中滚转角测量精度的指标要求。

参考文献（References）：

[1]Philippe W, Friedrich L, Lutz L, et al. Wind tunnel tests and open-loop trajectory simulations for a 155 mm canards guided spin stabilized projectile[C]//AIAA Atmospheric Flight Mechanics Conference and Exhibit. Honolulu,Hawaii, 2008: 881-898.

[2]Philippe W. Stability analysis for canard guided dual-spin stabilized projectiles[C]//AIAA Atmospheric Flight Mechanics Conference. Chicago, Illinois, 2009: 843-867.

[3]David J L. Estimation of the local vertical state for a guided munition shell with an embedded GPS/Micro-Mechanical inertial navigation system[D]. Cambridge,Massachusetts: MIT, 1995: 33-51.

[4]James M M. Efficient attitude estimation for a spin stabilized projectile[J]. Journal of Guidance, Control, and Dynamics, 2016, 39(2): 339-350.

[5]Park H Y, Kim K J, Lee J C, et al. Roll angle esti- mation for smart munition[C]//IFAC Symposium on Automatic Control in Aerospace. Toulouse, France: Pleiades Publishing. 2007: 6-12.

[6]Lee H S, Kim K J, Park H Y. Roll estimation of a smart munition using a magnetometer based on an unscented kalman filter[C]//AIAA Guidance Navigation and Control Conference and Exhibit. Honolulu, Hawaii: American Institute of Aeronautics and Astronautics. 2008:1-13.

[7]Adam R, Pecheur E, Bernard L, et al. In-flight roll angle estimation for a guided high spin projectile[C]//Sensors Applications Symposium. Catania, Italy, 2016: 308-313.

[8]王佳伟, 史凯, 徐国泰, 等. 基于扩展卡尔曼滤波的高转速修正引信滚转角测量方法[J]. 西北工业大学学报,2016, 34(6): 938-944.Wang J W, Shi K, Xu G T, et al. Roll estimation of high rotation speed correction fuze based on extended Kalman filter[J]. Journal of Northwestern Polytechnical University,2016, 34(6): 938-944.

[9]Thomas C, Stefer M, Bernard L. Roll angle estimation of a spinning object: experimental setup and preliminary results[C]// Proceedings of the International Conference on Microelectronics. Casablanca, Morocco, 2016: 1-4.

[10]Chang S J, Wang Z Y. Analysis of spin-rate property for dual-spin-stabilized projectiles with canards[J]. Journal of Spacecraft and Rockets, 2014, 51(3): 958-966.

[11]Julien S, Spilios T, Phillippe W. Flight control for a class of 155mm spin-stabilized projectile with reciprocating canards[C]//AIAA Guidance, Navigation, and Control Conference. Minneapolis, Minnesota, 2012: 685-694.