一类广义连续-离散系统量测丢失情况下鲁棒滤波算法

梁天添，王 茂

（哈尔滨工业大学 空间控制与惯性技术研究中心，哈尔滨 150001）

广义系统，又称描述系统或奇异系统，首先由著名学者H. H. Rosenbrock于20世纪70年代提出[1]，该系统的显著特征是在系统动态空间方程中可能存在奇异矩阵E。对于一些实际系统，诸如电气网络系统[2]、约束机械系统[3]、飞行器模型系统[4-5]，由于广义系统比空间描述方法具有更好的表述特性，该系统模型已得到越来越多的关注。针对广义系统的状态估计问题，先前的学者研究提出了诸如观测器设计等的有效解决方法[6-11]。但对于实际系统而言，噪声的存在是一个不可避免的挑战性问题。由于众所周知的原因，卡尔曼滤波方法能够有效解决有噪声系统的状态估计问题。但当系统量测发生异常时，卡尔曼滤波误差协方差矩阵可能发生变化，导致状态估计值与动态模型值产生较大偏差。目前，针对量测丢失情况下的广义连续-离散系统状态估计问题，现有解决方法仍然较少，本文正是基于该背景提出了一种研究方法。

基于卡尔曼滤波的有噪声广义系统状态估计问题，已有的研究工作能够保证该方法在广义系统上的可行性[12-17]。对于一般的广义系统模型，文献[12]提出了一种“双重方法”（dual approach），以推导出最优滤波器和相应的Riccati方程的“3块”（3-block）形式。文献[13]进一步提出基于递归重构算法的离散时间广义系统状态估计方法，该方法通过将估计问题转化为未来动态模型不影响当前状态的新的估计问题以实现一般离散时间广义系统的状态估计。文献[14]针对卫星姿态控制模型执行器故障诊断问题，设计了故障诊断广义卡尔曼滤波器，具体做法为：将卫星执行器故障视为增广广义系统中新增状态向量，并设计卡尔曼滤波器观测其状态，其实质仍是广义系统的卡尔曼滤波问题。文献[15]基于H∞滤波，针对含有未知输入的矩形广义系统（rectangular descriptor systems）设计了H∞广义卡尔曼观测器(HDKE)。文献[16]针对含有未知噪声协防差的广义系统设计了自校正全阶卡尔曼滤波器（self-tuning full-order Kalman filter）并推导其相应的广义 Riccati方程。进一步，文献[17]针对含有未知量测噪声协防差的多传感器广义系统设计了自校正全阶加权量测数据融合卡尔曼滤波器（self-tuning full-order weighted measurement fusion Kalman filter）。但是，已有的研究方法均无法避免在 Riccati方程中求解奇异矩阵E，导致后续求解过程非常繁琐。

对于转化得到的非奇异离散系统，当观测量出现异常时，由于量测残差发生变化，将导致卡尔曼滤波估计误差协方差矩阵发生变化，进而影响状态估计效果。文献[17]针对量测丢失情况下的不确定线性离散时间系统，提出了基于最优上界的鲁棒滤波方法，该上界能够确保卡尔曼滤波增益矩阵的收敛。本文在文献[18]已有研究基础上，针对量测丢失情况下的一类非线性广义连续-离散系统状态估计问题，提出了基于最优上界的鲁棒扩展卡尔曼滤波（REKF）方法，提出的最优上界用以保证转换得到的非线性一般离散时间系统动态模型新增不确定性在卡尔曼滤波误差协方差矩阵中有效收敛。

本文内容安排如下：第1节提出一类广义非线性连续-离散系统模型，引入参数并使用欧拉离散方法，将该广义系统转换为非奇异一般系统；第2节针对转换得到的非线性一般系统，当系统惯性测量元件的量测丢失时，提出扩展卡尔曼滤波（EKF）方法以实现非线性系统的线性化；由于第1节中的转换方式，导致在得到的非线性一般离散系统动态模型中存在新增不确定性，为解决该问题，第3节提出基于有限上界的REKF算法，以保证该不确定项不影响卡尔曼滤波增益矩阵收敛性，并能有效实现非线性广义连续-离散系统在惯性测量元件在量测丢失情况下的系统状态估计；第 4节提出仿真算例以验证该方法有效性；第5节得出结论。

1 问题描述

首先考虑正常情况下一类非线性广义连续-离散系统：

本文中，系统状态x假定满足如下关系式：

对于系统(1)，由于在动态模型中可能有奇异矩阵E，在卡尔曼滤波误差协方差计算时处理非常困难。为解决该问题，本文引入参数，将系统(1)转化为非奇异一般矩阵进行处理。

其中，T和N的通解[T N]可由式(4)求解得到：S为任意矩阵，代表设计自由度。

考虑本文提出的连续-离散系统模型，由于系统动态模型为连续变量，量测方程为离散变量，方程(3)不能直接使用。所以首先考虑将广义连续-离散系统转换为非奇异一般离散系统模型。

对于任意x(t)，基于式(3)，存在如下关系：

对式(5)使用欧拉离散化方法，则式(5)可重新表示为：

Ck为量测矩阵C在tk时刻采样值。采样间隔值τ取值充分小，以保证高阶项O(τ2) 忽略不计。

量测方程可表示为：

经以上处理，系统(1)可重新表示为：

式(7)可重新表示为：

考虑式(9)，式(8)可重新表示为：

式中，wk、vk分别为均值为 0且相互独立的高斯白噪声，其误差协方差矩阵分别表示为：

定义：

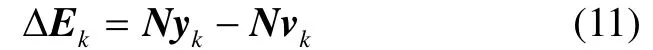
将式(11)代入式(10)中，式(10)可重新表示为：

以下假设用以保证广义系统卡尔曼滤波可行性。

2 观测量丢失时扩展卡尔曼滤波

当系统(1)观测量丢失时，其等价系统(12)可重新表示为：

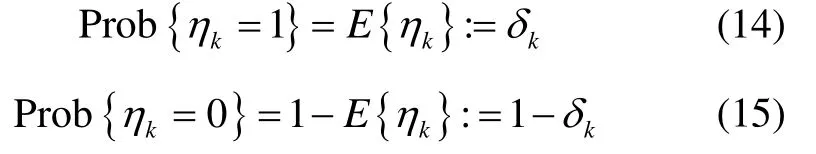
其中，kδ∈R为已知正标量，kη、wk、vk相互独立。

为实现系统(13)的状态估计，本节提出鲁棒扩展卡尔曼滤波（REKF）算法，其中，扩展卡尔曼滤波算法（EKF）的形式同样适用于REKF算法。

系统(13)存在如下形式滤波器：

估计误差和误差协方差矩阵可表示为：

为找到最优上界Pk，使式(20)成立：

预测误差和预测误差协方差可表示为：

将系统(13)中动态模型方程代入(21)可得：

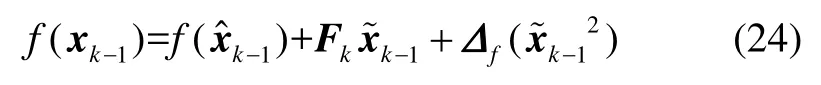
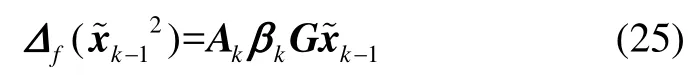
G∈Rn×n用以调节滤波器参数。

考虑式(24)和式(25)，式(23)可重新表示为：

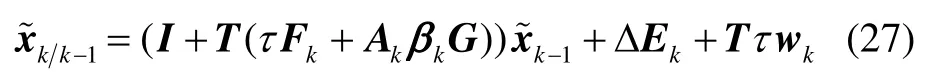
ΔEk可进一步处理为：

其中，kα与kβ类似，假设kα满足如下不等式：

将式(28)代入式(27)可得：

将式(30)代入式(22)可得：

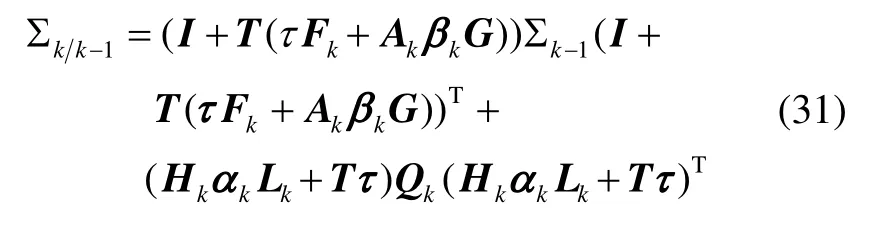
考虑系统(13)中量测方程， 并将式(17)代入式(18)可得：

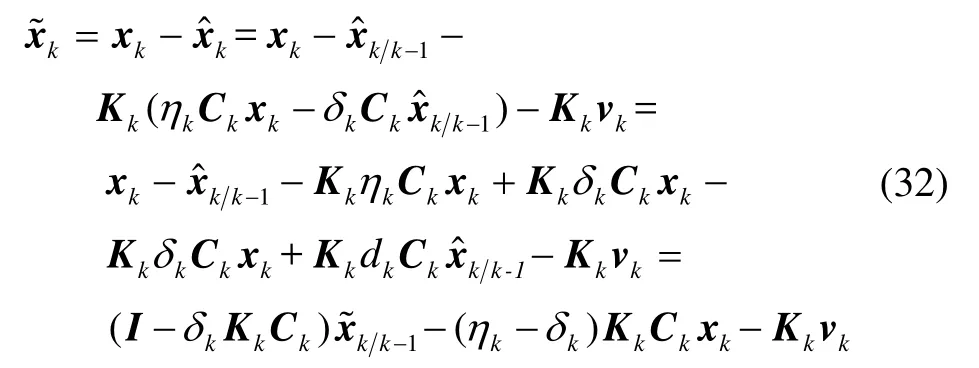
将式(32)代入式(19)可进一步得到：

考虑式(2)，式(33)可进一步表示为：

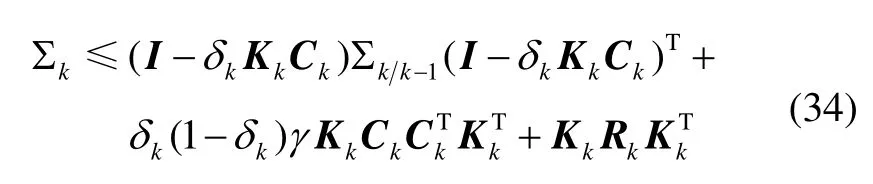
当Kk取得极值时∑k取得最大值，则有：

由式(35)可得：

尽管从推导可以得到卡尔曼滤波误差协方差矩阵，由于式(25)与式(28)存在，kβ、kα未知，很难直接求解∑k。为解决该问题，提出引理1。

引理1[18]：已知矩阵其中TD D≤I，X是正定矩阵，如果存在任意α＞0使得：

成立，则以下不等式成立：

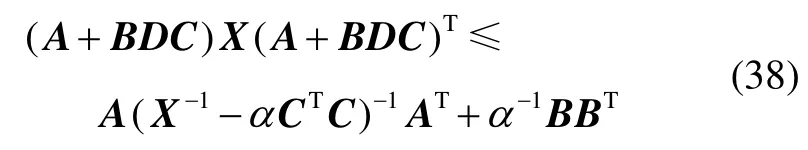
基于引理1，式(31)可重新表示为：

其中，μ和λ为已知的设计参数。

从REKF算法推导过程可知，对于量测丢失情况下的广义连续离散系统(1)，其等价系统(13)的状态估计REKF算法滤波流程如下：

1）一步预测及相应的误差协方差矩阵由式(18)及式(31)得到；2）状态估计值及相应的误差协方差矩阵由式(19)及式(34)得到；3）基于最优上界，卡尔曼滤波增益可由式(40)计算得到。

3 仿真分析

考虑如下广义连续-离散系统模型：

其中，w、v为随机分布白噪声，为保证采样精确，惯性测量元件的采样间隔设为τ=0.1s。

仿真初始条件选择如下：

式(3)的T和N值：

显然，T为非奇异矩阵。

为保证REKF算法鲁棒性，μ、F、G取值如下：

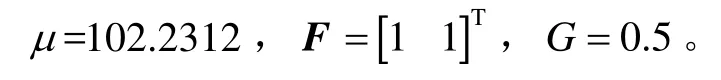
为保证ΔE在鲁棒算法中收敛性，λ、H、L取值如下：

得到的系统状态如图1所示。

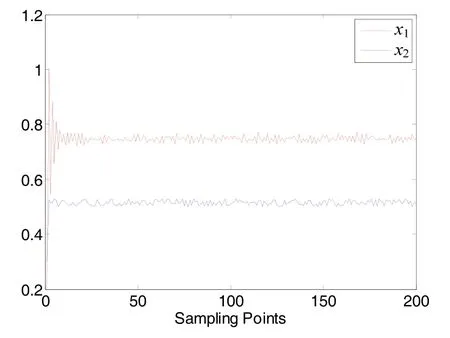
图1 x1及x2状态Fig.1 States ofx1andx2

如上文所述，鲁棒滤波算法优越性在于其能够保证卡尔曼滤波误差协方差矩阵收敛性。本文针对如式(41)所示的系统，通过传统EKF算法与REKF算法得到的状态估计误差进行对比的方法，来验证所提出的REKF算法的优越性。

仿真平台：Intel(R) Core(TM) i5-3210M CPU@2.50 GHz，8 GB 内存IBM计算机；

仿真软件：Matlab软件。

仿真采用Monte Carlo仿真方法，EKF和REKF算法每百次运算时间如表1所示。

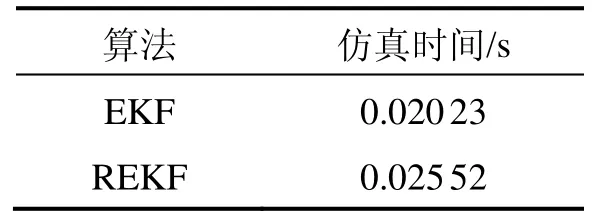
表1 每次运算计算时间Tab.1 Calculation time

针对式(41)所示系统，由EKF及REKF算法得到的状态估计误差如图2及图3所示。

使用 EKF及 REKF算法得到的均方根误差（RMSE）如表2所示。

图2 x1估计误差（EKF与REKF对比图）Fig.2 Estimation error ofx1(EKF versus REKF)

图3 x2估计误差（EKF与REKF对比图）Fig.3 Estimation error ofx2(EKF versus REKF)

表2 EKF及REKF均方根误差Tab.2 Root mean square errors of EKF and REKF

从图2及图3可知，本文提出的REKF算法保证了新增不确定性ΔE在滤波误差协方差矩阵中的收敛性，相较于EKF算法，能够更好地对系统状态进行估计。通过对比可知，相较于EKF算法，REKF算法对范数有界的广义连续-离散系统状态估计更具精确性。分析表1可知，尽管REKF算法在仿真时间上更长，但与EKF算法相比，仿真时间增加量为超过13%，证明REKF算法在提高了仿真精度的同时，对仿真时间影响较小。分析表 2可知，通过 REKF算法得到的RMSE仅为EKF算法得到的RMSE的1/5，进一步证明了REKF算法对所提出的系统状态估计的精确性。

4 结 论

针对惯性测量元件的量测丢失情况下的一类范数有界的有噪声非线性广义连续-离散系统，提出一种基于鲁棒扩展卡尔曼滤波（REKF）算法的状态估计方法。首先引入参数，使用欧拉离散化方法将理想状态下的广义连续-离散系统转化为非线性非奇异一般离散时间系统。其次，当转化的等价系统量测丢失时，提出扩展卡尔曼滤波（EKF）方法以解决非线性问题，针对使用的转化方法所导致的新增不确定性，提出基于EKF算法的REKF算法，以保证新增不确定性不影响滤波误差协方差矩阵收敛性。最后，提出仿真算例。仿真算例验证了对于量测丢失情况下的非线性广义连续-离散系统状态估计问题，提出的REKF算法相较于EKF算法具有更高的精确度。

参考文献（References）：

[1]周振华. 参数不确定广义分段仿射系统的鲁棒控制和滤波[D]. 哈尔滨: 哈尔滨工业大学, 2016: 1-8.Zhou Z H. Robust control and filtering for singular piecewise-affine systems with norm-bounded uncertainties[D]. Harbin: Harbin Institute of Technology, 2016: 1-8.

[2]Wang Z H, Shen Y, Zhang X L, et al. Observer design for discrete-time descriptor systems: an LMI approach[J].Systems & Control Letters, 2012, 61(6): 683-687.

[3]王振华, 描述系统的故障诊断观测器设计[D]. 哈尔滨,哈尔滨工业大学, 2013: 19-23.Wang Z H. Fault diagnosis observer design for descriptor systems[D]. Harbin: Harbin Institute of Technology, 2013:19-23.

[4]Lai Y B, Lu G P. A novel observer for nonlinear des-criptor jumping systems with communication time delay[C]//36th Chinese Control Conference. 2017: 482-487.

[5]陈诚, 王小刚, 秦武韬, 等. 基于鲁棒滤波的无人机着陆相对导航方法[J]. 中国惯性技术学报, 2017, 25(3):415-420.Chen C, Wang X G, Qin W T, et al. Unmanned aerial vehicle landing navigation algorithm based on robust filter[J]. Journal of Chinese Inertial Technology, 2017,25(3): 415-420.

[6]Jia Q X, Li H Y, Zhang Y C, et al. Robust observer-based sensor fault reconstruction for discrete-time systems via a descriptor system approach[J]. International Journal of Control, Automation, and Systems, 2015, 13(2): 274-283.

[7]Aouaouda S, Chadli M, Shi P, et al. Discrete-timeH-/H∞sensor fault detection observer design for nonlinear systems with parameter uncertainty[J]. International Journal of Robust and Nonlinear Control, 2015, 25(3): 339-361.

[8]Kulan Z, Ma S P, Zhu L P, et al. RobustH∞filtering for nonlinear discrete time-delay Markov jump descriptor systems[C]//29th Chinese Control and Decision Conference. 2017: 985-990.

[9]Yan Y Y, Liu Y M, Yang M S, et al. Finite frequency fault detection observer design for uncertain descriptor systems[C]//36th Chinese Control Conference. 2017: 7351-7357.

[10]Wu Y K, Jiang B, Lu N Y. A descriptor system approach for estimation of incipient faults with application to high-speed railway traction devices[J]. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2017,PP(99): 1-11.

[11]Yin S, Gao H J, Qiu J B, et al. Descriptor reduced-order sliding mode observers design for switched systems with sensor and actuator faults. Automatica, 2017, 76: 282-292.

[12]Nikoukhah R, Willsky A S, Levy B C. Kalman filtering and Riccati equations for descriptor systems[J]. IEEE Transactions on Automatic Control, 1992, 37(9): 1325-1342.

[13]Nikoukhah R, Campbell S L, Delebecque F. Kalman filtering for general discrete-time linear systems[J]. IEEE Transactions on Automatic Control, 1999, 44(10): 1548-1552.

[14]Wang Z H, Shen Y, Zhang X L. Attitude sensor fault diagnosis based on Kalman filter of discrete-time descryptor system[J]. Journal of Systems Engineering and Electronics, 2012, 23(6): 914-920.

[15]Hsieh C S. H-infinity Kalman estimation for rectangular descriptor systems with unknown inputs[J]. IEEE Transactions on Automatic Control, 2014, 59(3): 826-832.

[16]Ran C J, Dou Y F, Gao Y. Self-tuning full-order Kalman filter for descriptor system[C]//35th Chinese Control Conference. 2016: 1808-1813.

[17]Dou Y F, Sun S L, Ran C J. Self-tuning full-order WMF Kalman filter for multisensor descriptor systems[J]. IET Control Theory & Applications, 2016, 11(3): 359-368.

[18]Mohamed S M K, Nahavandi S. Robust finite-horizon Kalman filtering for uncertain discrete-time systems[J].IEEE Transactions on Automatic Control, 2012, 57(6):1548-1552.

[19]Kai X, Wei H L, Liu L D. Robust extended Kalman filtering for non-linear systems with stochastic uncertainties[J]. IEEE Transactions on systems, Man, and Cybernetics: Systems and Humans, 2010, 40(2): 399-405.