例析用导数求切线方程的几种类型

马涵坤

(河北省衡水第一中学 053000)

用导数求曲线的切线方程的方法为：设P(x0,y0)是曲线y=f(x)上的一点，则以P为切点的切线方程为y-y0=f′(x0)(x-x0)．当曲线y=f(x)在点P(x0,f(x0))的切线平行于y轴(即导数不存在)时，由切线定义知，切线方程为x=x0．下面例析几种常见的类型及解法.

类型一：已知切点，求曲线的切线方程

题目中点明切点，只需求出切线的斜率,并代入点斜式方程即可．

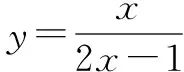
A.x-y-2=0 B.x+y-2=0

C.x+4y-5=0 D.x-4y-5=0

分析求出导数，求得切线的斜率，由点斜式方程可得切线的方程．

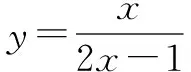
可得在点(1，1)处的切线斜率为-1.

则所求切线的方程为y-1=-(x-1)，

即为x+y-2=0．

故选B．

点评正确求导和运用点斜式方程是求切线方程的关键．

类型二：已知斜率，求曲线的切线方程

题目中未明确切点，需要利用题中条件求出切点，再确定切线的斜率，最后用点斜式方程加以求解．

例2 与直线2x-y+4=0平行的抛物线y=x2的切线方程是____．

分析根据导数的几何意义求出函数f(x)在x处的导数等于切线的斜率，建立等式，求出x的值，从而求出切点坐标，最后将切线方程写出一般式即可．

由此得到切点(1，1).

故切线方程为y-1=2(x-1)，即2x-y-1=0．

点评本题主要考查了利用导数研究曲线上某点处的切线方程，同时考查化归与转化思想.另外此题所给的曲线是抛物线，故也可利用Δ法加以解决．

类型三：已知过曲线上一点，求切线方程

题目中给出了曲线上的任一点，但该点未必是切点，故要先求出切点，再利用斜率，就可求出切线的方程了．

例3 求过曲线y=x3-2x上的点(1，-1)的切线方程．

分析求导数，设切点坐标，利用导数的几何意义求切线方程即可．

解设P(x0,y0)为切点，

所以切线方程为：y-y0=(3x02-2)(x-x0)，

即y-(x03-2x0)=(3x02-2)(x-x0).

又知切线过点(1，-1)，

将其代入上述方程，得

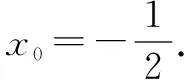
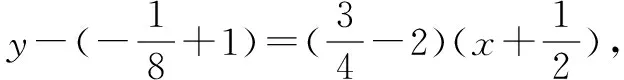
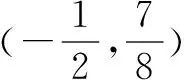
类型四：已知过曲线外一点，求切线方程

当给出的已知点不在曲线上时，需要先求出切点，再用待定切点法来求解．

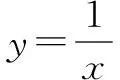
分析设出切点(m,n)，求得导数，可得切线的斜率，由点斜式表示出切线方程，代入已知点，就可求出切点，从而求出切线方程．

解设P(x0,y0)为切点，

又已知切线过点(2，0)，

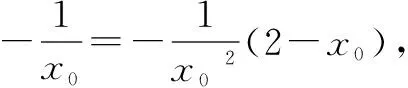
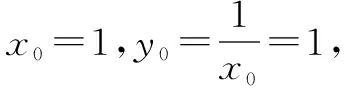
点评点(2，0)实际上是曲线外的一点，但在解题过程中却无需判断它的确切位置，只需区分“过点”与“在点”即可，这充分反映出待定切点法的高效性．

通过以上分析，希望同学们能够掌握利用导数求切线方程的各种类型.在不同的条件下，利用不同的思路完美地解决问题.

参考文献：

[1]桑观赏.用导数求切线方程的四种类型[J].中学生数理化(高二版)， 2012(Z1).