含参不等式的恒成立、恰成立与能成立

杨奇华

(浙江省宁波市北仑区柴桥中学 315000)

含参不等式成立条件下，求参数取值范围问题一直是高考及模拟考试中的热点题型.但不等式成立的形式却有不同，如果理解不透极易导致误解.本文通过例子解析不等式成立的几种不同形式，以识别题型、理清思路，正确求解.

一、f(x)≥a的恒成立与恰成立

例1 已知f(x)=x2+(m+1)x+1,x∈[0,+∞).

(1)若f(x)≥0恒成立，求m的取值范围；

(2)若f(x)≥0恰成立，求m的取值范围.

解(1)f(x)≥0恒成立，即x2+(m+1)x+1≥0在x∈[0,+∞)时恒成立.

①当x=0时，上述不等式显然成立，所以m可为任意实数.

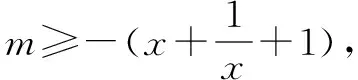
综上①和②，要使x∈[0,+∞)时不等式都成立，则m的取值范围是m≥-3.

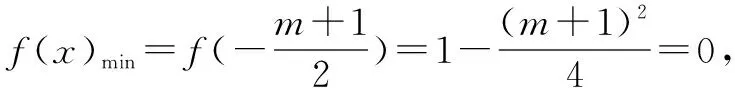
注意到题设f(x)的定义域是[0,+∞),

①当m=1时，f(x)=x2+2x+1=(x+1)2，可知x=0时，f(x)min=f(0)=1，这题设的f(x)≥0恰成立不符，故m=1不合题意，应舍去.

②当m=-3时，f(x)=x2-2x+1=(x-1)2，可见x=1时，f(x)取得最小值是f(1)=0，即f(x)≥0恰成立，符合题意.

综上①和②，得m=-3.

点评若f(x)≥a恰成立，则要求f(x)的最小值恰好是a;而f(x)≥a恒成立，要求f(x)的最小值大于或等于a.本例在解答时，要注意定义域的作用，应检验m的取值是否满足定义域的要求.

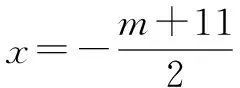
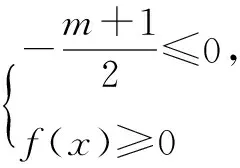
解得m≥-1或-3≤m<-1，从而得m≥-3.

二、不等式的恒成立与能成立

例2 已知f(x)=8x2+16x-k,g(x)=2x3+5x2+4x.

(1)若对任意x∈[-3,3]都有f(x)≤g(x)成立，求k的取值范围；

(2)若对x1∈[-3,3],x2∈[-3,3]都有f(x1)≤g(x2)成立，求k的取值范围；

(3)若存在x∈[-3,3]，使f(x)≤g(x)成立，求k的取值范围；

(4)若存在x1∈[-3,3],x2∈[-3,3]，使f(x1)≤g(x2)成立，求k的取值范围.

解(1)题设条件f(x)≤g(x)成立，即h(x)=g(x)-f(x)=2x3-3x2-12x+k≥0对x∈[-3,3]恒成立，故只要h(x)min≥0.不难求得h(x)在[-3,3]上的最小值h(x)min=h(-3)=k-45.由k-45≥0，得k≥45.

(2)本小题中的x1与x2并无关联，因此f(x1)≤g(x2)恒成立⟺当x∈[-3,3]时，f(x)max≤g(x)min.当x∈[-3,3]时，不难求得f(x)max=f(3)=120-k,g(x)min=g(-3)=-21.那么由120-k≤-21,得k≥141.

(3)存在x∈[-3,3]使f(x)≤g(x)能成立，即不等式h(x)=g(x)-f(x)≥0在[-3,3]上有解，故只要h(x)max≥0即可.不难求得h(x)max=h(-1)=k+7.由k+7≥0，得k≥-7.

(4)注意到x1与x2彼此无关，要使不等式f(x1)≤g(x2)能成立，只要有f(x)min≤g(x)max.不难求得当x∈[-3,3]时，f(x)min=f(-1)=-8-k,g(x)max=g(3)=111.由-8-k≤111,得k≥-119.

点评要仔细辩别本例中4个小题的区别与联系，才能准确理解题意，避免误解错答.

(1)小题属于“任意型恒成立”问题，要求不等式永远成立，因此只要有h(x)min≥0即可.

(3)小题属于“存在型能成立”问题，要求不等式有解即可，因此只要有h(x)max≥0.

(2)、(4)小题中的x1与x2是彼此独立的，并不要求x1与x2是同一个值，因此不能用构造函数h(x)=g(x)-f(x)来解答，而应分别考虑f(x)、g(x)的最大最小值.

参考文献：

[1]刘鹏.参数取值范围问题的求解方法[J].高中数学教与学，2014(1)：19～21.

[2]滕仲华，章才良.例析“分离参数法”在含参不等式中的应用[J].福建中学数学，2014(4)：42-44.

[3]吴佐慧，林军，刘合国.高考全国卷含参不等式恒成立问题的探究[J].中学数学，2014(2)：85～87.