一道导数试题的解法探究

冀柯维

(河北省衡水第一中学 053000)

函数与导数是高中数学中极为重要的内容，是高考考查的重点内容.由于函数与导数可以与三角函数、不等式、数列等知识融合考查，所以其解题方法也多种多样.下面通过一道典型试题探究一下这类问题的解法.

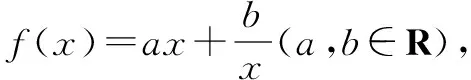
(1)用a表示b；

1.试题分析

这是一道“高研值”的好题，其注重知识方法的基础性又兼顾问题的综合性，充分展现了问题的检测与选拔功能.第(1)问考查导数的几何意义，属于常规问题；第(2)问的(ⅰ)问涉及恒成立问题，求解过程相对复杂，有一定的难度；第(2)问的(ⅱ)问考查不等式的证明，它将三角函数、不等式、导数等知识融于一题，入手虽较易，但思维含量较高，不易得证.

2.解法探究

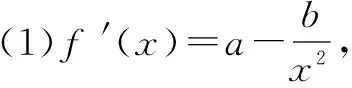
(2)(ⅰ)解法一：导数方法求最值，分类讨论有标准

处理不等式的恒成立问题时，通常情况下可转化为函在给定区间上的最值问题去分析，即若f(x)≥a恒成立⟺f(x)min≥a；若f(x)≤a恒成立⟺f(x)max≤a.利用导数求函数的最值，一般按以下步骤进行：先求导数，并求得导数的零点，再以导数的零点为界划分定义域为若干区间，并判断导数在每一区间上的符号，进而得到函数的单调区间与极值、最值.在求导数的零点时，在划分定义域时，在判断导数符号时，在确定最值时，往往需结合参数的取值范围分类讨论.把握好分类讨论的标准，是正确求解的关键所在.

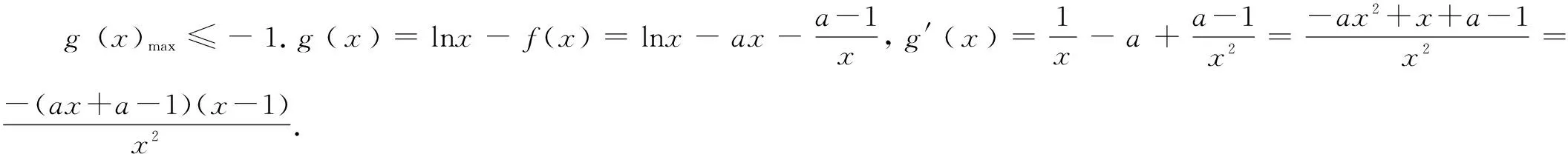
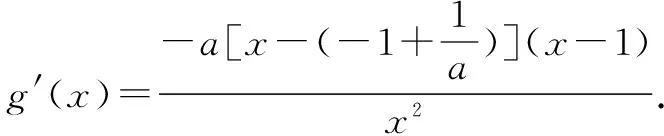
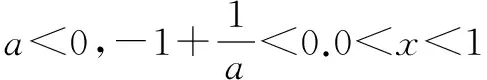
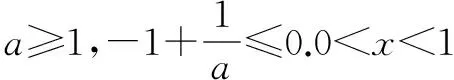
综上，实数a的取值范围为[1,+).

解法二：参变分离构函数，分拆放缩求范围

处理不等式的恒成立问题时，应优先考虑参变分离法.这样做的优点是：把含参的函数问题转化为不含参数的函数问题，避免了分类讨论.实施参变分离后出现新函数，习惯思维定式是直接对函数求导找最值，经演算发现导数的零点不可求，此时“再次求导”为问题的破解提供有力的支撑，尝试后仍然不可解，陷入惯性思维的“怪圈”不能自拔，似乎到了“山穷水尽”的境地，此时，分拆函数放缩往往能打开“绝处逢生”的神奇通道.放缩是导数问题中转化的有效方法，可以避免不必要的繁琐过程，又可快速解决问题而不失严谨性.关键在于对式子结构的分析和对常用不等式的熟悉，如：lnx≤x-1，ex≥x+1等等，不再赘述.不过应用不等式时，要注意变量的范围和不等式的方向，所以要拆分变形出合适的形式，方便进行合理的放缩以及后续的运算.

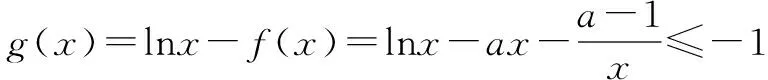
综上，实数a的取值范围为[1,+).

解法三：联想特殊与一般，先验再证破疑难

特殊化与一般化思维贯穿于整个解题过程之中，就一般化而言，应努力去引出一般的结论，揭示其内在的依据，并作出可能的推广.而特殊化思想则可用于解决一些抽象、概括性极高的问题，若直接发现或论证感到困难时，可以先试探它的特殊、局部情况的特性，找到解题的突破口，从中发现规律并顺利解题.由解法一可以看出由于参数a范围的不确定性，使得解题过程冗长.解题的关键是按照题目设计的问题步步深入，通过特例赋值分析，悟出由特殊到一般的思维方法，探索出参数a的大致范围，避免了繁琐的分类讨论，问题也就迎刃而解了.

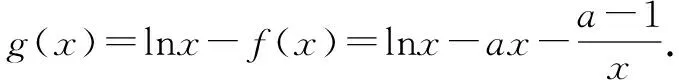
g(x)≤-1恒成立，即g(1)=-a-(a-1)≤-1⟹a≥1.

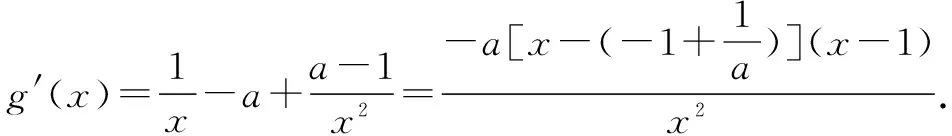
则g(x)max=g(1)=1-2a≤-1，符合题意.

综上，实数a的取值范围为[1,+).

不等式的证明是高中数学的重要内容，也是高中数学的一个难点，加之题型广泛，涉及面广，证法灵活，备受命题者青睐.比较法是不等式证明的最基本方法，包括作差法和作商法，综合法与分析法的应用反映了对已知条件和所学知识的驾驭能力.

由(ⅰ)知a≥1，令sinθ=t∈[0,1).

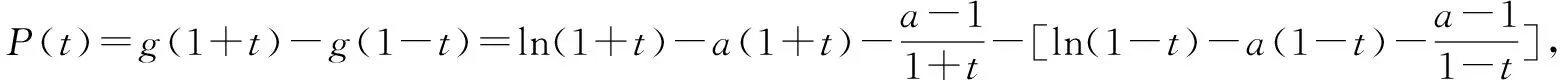
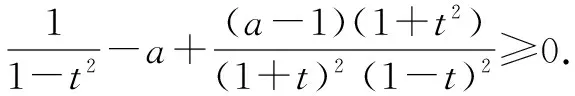
参考文献：

[1]周丽娟.一道导数试题的解法探究[J].中学数学研究,2014(21).