高中物理解题中“微元法”的运用实践分析
2018-05-09赵烨程
赵烨程
(山东省章丘市第四中学 250200)
所谓微元法,即学生面对物理问题进行解决时,将物理解题过程进行分解,使其能够成为多个微小的元对象,或是元过程,因为不同的元对象以及元过程在解题时都要遵循固定的规律,因此,实际分析时只需要针对其中某个元对象或者元过程进行即可,随后再将其通过物理或者是数学思想进行解决,便可得到最终答案.微元法的应用,更多是对物理问题的分析与解决,是多种解题方法中最为有效的一种,解题过程体现了由部分到整体的规律,也是学生需要掌握的重要方法.
一、微元法
在物理解题中应用微元法,是一种非常有效的解题方法,其中微元法中的“微”,指的是一个非常短暂的过程,“元”既体现了独立性,同时也可以对物理解题的过程进行反映.换而言之即在整体中划分细微的局部,按照一些内在联系以及规律通过局部对物理习题进行了解,进而完成解题.当然这是从物理角度进行了解,在数学角度分析,微元法其实是积分与极限近似的一个过程,通过微元的叠加获得结果.
二、微元法解题流程
1.取元
运用微元法的过程中,最为重要的便是“元”,所以取元也是所有解题过程中最为重要的一个步骤,若取元效果不好,便会对最终结果造成影响,并且也会在原来的基础上加大解题难度.基于此,需要注意以下几点:① 取元时务必要明确所要取的“元”在计算时具有简单性,若“元”在求解上具有一定难度,便从根本上丧失了微元法应用的意义.② 保证取元可以在叠加下获得结果.这里提到的叠加主要包含了两个方面的含义.其一是指加权叠加,即对各个“元”进行计算的过程中务必要对其自身的权重进行考虑;其二,进行取元主要是为了能够获得物理习题的最终结论,所以取的“元”经过叠加之后需要代表整体,不能重复也不能遗漏.③ 取“元”需要有特定的规律,可以利用这一规律完成加权叠加.对微元进行理解时,其本身是一个极限的概念,也就是可以将其理解为无限小.运用于物理解题中,选取的“元”也不受限,可以是一个线段,也可以是一段弧,通过Δ这一符号对其进行表示,如时间元即Δt.
2.模型化
取完“元”之后,便要将取的“元”利用近似过程转变为可以简单求解的过程.其实模型化也就是利用近似相等或极限相等的方式将复杂问题降低难度,以更加简单的方式建立一个正确的模型,进而得到最终结论.
3.求和
完成各个“元”的计算之后,便要将其进行叠加求和,从而计算出最终结果.这一叠加计算的过程中属于数学范畴,即对数学求和公式进行应用.对每个“元”进行求和时,需要注意的是要将所有“元”都进行计算,在求和公式中进行数学变形,可以降低计算的难度.
三、高中物理解题中“微元法”的运用
1.质量元△m
若在解题中出现质量元,且规律相同,那么便要遵循所体现的解题方法,将这一习题分解成为多个质量元,选择计算最为简单的元最为研究对象进行计算,随后根据上文介绍的流程获得表达式,计算最终结果.
例1 在一辆加速启动状态的火车中放置了一桶水,测量发现水面和汽车所行驶的水平路面形成夹角为θ,如图1所示,那么求解汽车在加速度行驶的那一段期间的加速度大小?
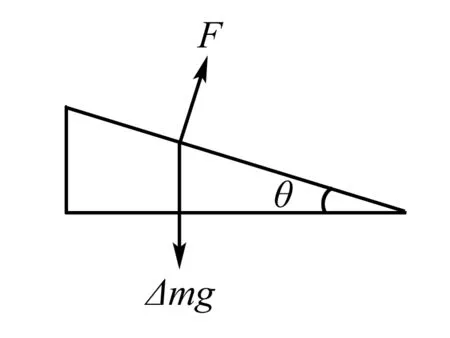
图1
解析:在对这一问题进行求解时,可以从水面中着手获取解题所需的水“质量元”,将水的质量设为△m,车厢内部水受力情况如图1所示,若F合=△mgtanθ,根据牛顿第三定律便可以求得以下结论,由于F合=△ma.所以a=gtanθ,并且方向与汽车的启动方向保持一致.
2.时间元△t
在物理解题过程中“时间”十分常见,也是物理习题中最普遍的条件之一,通过实际解题发现,除了时间以外,其余相关变量若脱离了微元法,那么便会提高解题难度,常规的解题方法不仅运算过程繁琐,并且十分容易出错,因此对于△t而言,采用微元法进行解决是学生必须要掌握的方法之一.
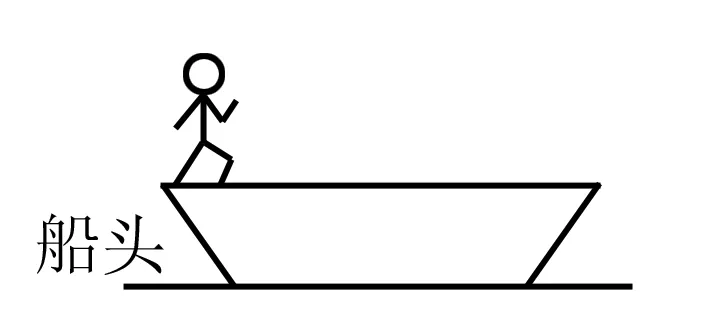
图2
例2 如图2所示,一艘长度为L的船静止于平静的水面,有一人立于船头,且该人的质量是m,船质量则是M,如果不计水阻力,那么 人由船头走至船尾的这一阶段,求解船位移距离?
解析将人与船这一整体视为研究系统,人处于走动的状态下,系统受合外力是零,由此可知系统动量守恒.假设人处于走动状态下的△t时间内是匀速运动,由此便可以计算出船位移.
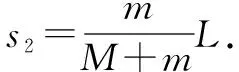
3.张力
例3 根据图3求绳子的张力.
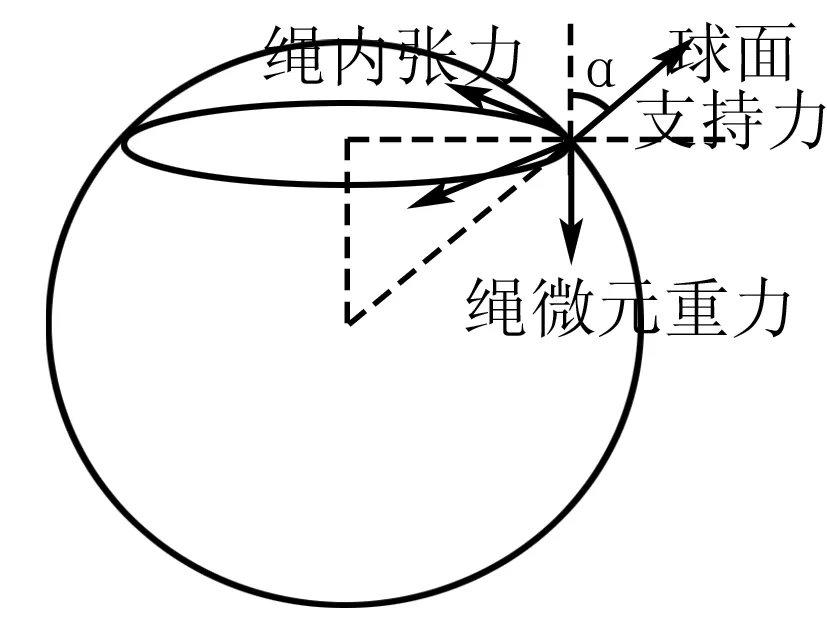
图3
解析将最右边一小段的绳子作为微元,根据图3分析受力.若想求弹力常数K,又已经知道绳子的伸长,因此必须知道弹力大小.弹力的大小可由空间力平衡来求,在弹力这个平面上,也就是顶端圆面上,只有支持力N的分力,而大小位置,因此需要先求出N的大小,N的大小可以通过重力方向上的力学平衡得出,重力已知,因此可以求解.
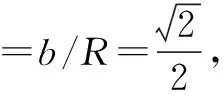
在圆截面方向列力的平衡:设绳微元的张力为F,从顶端俯瞰截面圆,如图4:
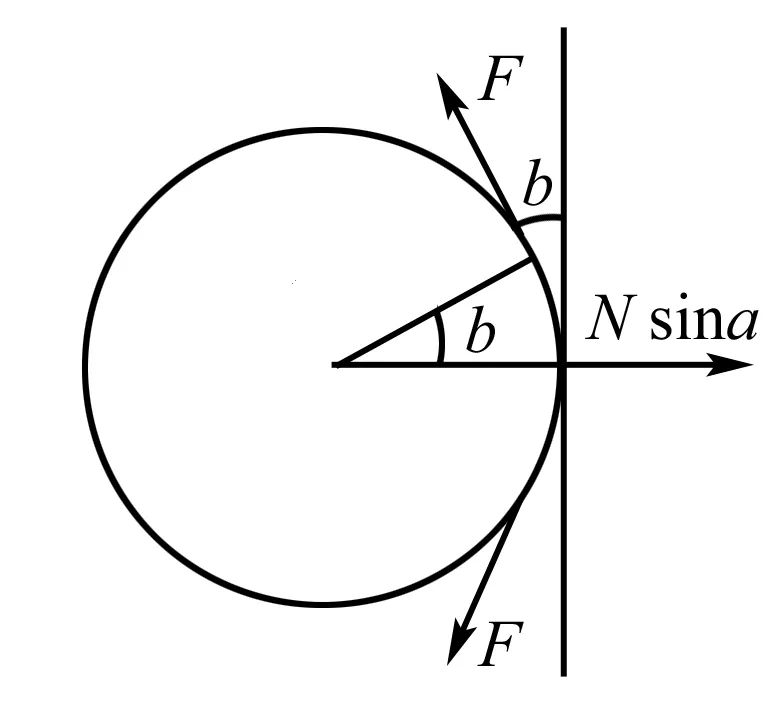
图4
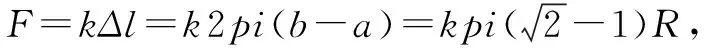
综上所述,在高中物理解题中运用微元法,一方面可以降低题目难度,另一方面可以锻炼学生思维能力,通过微元法的运用真正提高自身物理解题水平,进而培养物理综合素质.
参考文献:
[1]周笑春. 高中物理教材中微元法的体现和应用[J]. 求知导刊,2015(07):137.
[2]李从明. 微元法在高中物理中的应用[J]. 教育教学论坛,2010(17):42-43.
[3]高越. 微元法在高中物理解题中的应用[J]. 佳木斯教育学院学报,1999(01):54-57.
[4]邱建忠. 微元集合法在物理解题中的应用[J]. 湖南科技学院学报,2012(04):57-59.
