函数多元问题的解法探究

张笑晗

(河北省辛集中学 052360)

题目已知函数f(x)=axlnx(a≠0)，

(1)求函数f(x)的单调区间和最值；

(2)若m>0,n>0,a>0,证明：f(m)+f(n)≥f(m+n)-a(m+n)ln2.

分析本题是一道导数的练习题，数量关系看似简单，实质上不尽然.第(1)问考查利用导数确定含参函数的单调性和最值，属常规题型；第(2)问考查含有多个参变量的不等式的证明，初读题目往往会感到无从下手或陷入繁琐的运算之中.解题的关键有两个转化难点：一是参数a如何分类讨论，二是三个参数m、n、a向哪个方向转化.笔者从不同的角度去思考问题，探究多种解法.

解法探究(1)求函数f(x)的单调区间和最值

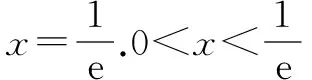
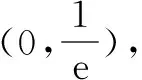
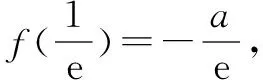
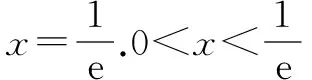
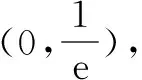
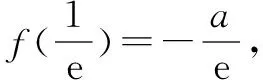
(2)若m>0,n>0,a>0.证明：f(m)+f(n)≥f(m+n)-a(m+n)ln2.

解法一：直接赋值构造函数

对于证明与函数有关的含多个参变量的不等式时，常常需要构造辅助函数，通过求导研究其单调性或寻求其几何意义来解题.题目本身特点不同，所构造的函数可有多种形式，解题的繁简程度也因此而不同.正确分析函数不等式的结构，恰当构造函数成为解题的突破口.

通过分析题目条件，发现涉及的三个函数f(m)、f(n)、f(m+n)中都含有参变量a，提取公因式结合a的取值范围进而定号，只剩两个参变量m和n，可以考虑将其中一个参变量赋值x，另一个看成常数，构造出新函数，问题就迎刃而解了.

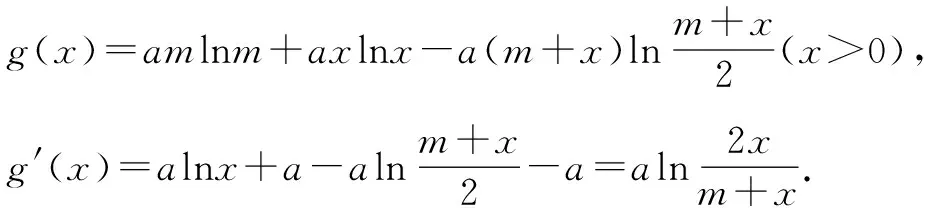
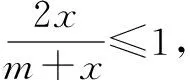
∴g′(x)≤0，g(x)单调递减.

∵m≥x>0，∴g(x)≥g(m)=0，

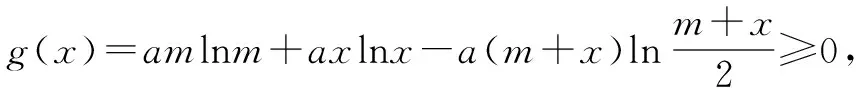
即f(m)+f(n)≥f(m+n)-a(m+n)ln2.

解法二：统一变量构造函数

在数学解题过程中，如果我们总是能尝试以不同的视角分析并解决同一个问题，会帮助我们理解知识之间的关联，对学习产生积极的作用.消元构造函数是解决含多变量函数的一种有效方法，通过消元这一方法的实施，求解问题的思路也就逐渐明朗起来，从而使问题得以顺畅解决.实际上，我们可以通过确定两个参变量m和n之间的比例关系，统一成一个变量代入求解，构造出新函数，讨论也就有了方向.

不妨设m≥n>0,则m=kn(k≥1).

左边-右边=a[mlnm+nlnn+(m+n)ln2-(m+n)ln(m+n)]

∴g(k)在k∈[1,+)上单调递增，∴g(x)≥g(1)=0.

又∵n>0,a>0,∴左边-右边≥0，

即f(m)+f(n)≥f(m+n)-a(m+n)ln2.

解法三：借琴生不等式构造函数

琴生不等式(也称为詹森不等式)：

(1)设f(x)为凸函数，对于其定义域上的n个数x1,x2,…,xn，都有

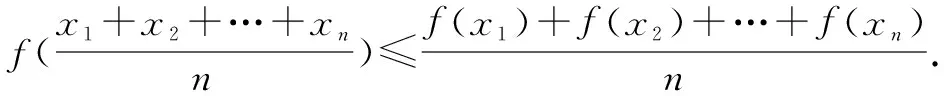
(2)设f(x)为凹函数，对于其定义域上的n个数x1,x2,…,xn，都有

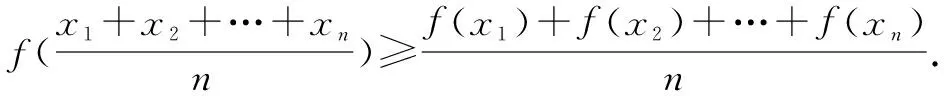
通常情况下用初等方法判断函数的凹凸性比较麻烦，不过如果利用数学分析我们可以有个非常方便的结论：

如果f(x)二阶可导,且f″(x)≥0,那么是下凸函数(凸函数);

如果f(x)二阶可导,且f″(x)≤0,那么是上凸函数(凹函数).

有了这个结论以后,使用琴生不等式就非常方便了.解题关键是对不等式形式的结构特征有严格要求，识别是前提，转化靠联想.

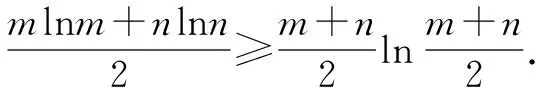
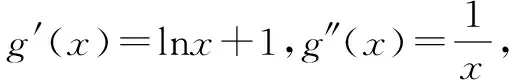
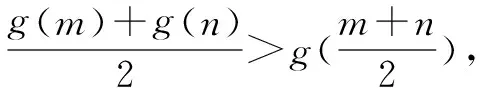
参考文献：

[1]赵优良.例析多元参数的函数综合问题解法[J].中学生数学，2017(03).