关于层状岩体抗拉强度测定方法的讨论

刘 伟，曾亚武，陈 曦，任树林

(武汉大学 土木建筑工程学院， 湖北 武汉 430072)

抗拉强度是岩体的基本力学参数之一，对于了解岩体力学性能非常重要。在实际工程中岩体受拉的情况也随处可见，因为岩石的抗拉强度一般都远低于其抗压强度，因此，岩体受拉破坏也是常见的破坏类型。地下洞室和巷道的开挖会引起周围地应力的重新分布，在拱顶或者边墙部位容易出现拉应力[1]；人工边坡表面附近，由于自由面的存在，拉应力也经常存在[2]；在煤矿开采或者巷道掘进过程中，冒顶、冲击地压和煤与瓦斯突出等动力灾害事故时有发生，这些往往也与煤岩层受拉破坏相关[3]。因此，准确的测定工程相关岩体的抗拉强度，对工程和人员安全均有重要意义。

岩体抗拉强度的测定方法有多种[4]：巴西劈裂法、直接拉伸法、正方形板对轴压裂法、对轴压膜拉伸法、圆盘弯曲拉伸法和条状岩梁弯曲拉伸法等，但常用的是巴西劈裂法和直接拉伸法。在《铁路工程岩石试验规程》[5](TB 10115—2014)、《公路岩石试验规程》[6](JTG E41—2005)和《水电水利工程岩石试验规程》[7](SL 264—2001)中岩石抗拉强度试验都是推荐采用巴西圆盘劈裂法(Brazilian test)，且所给出的适用条件均为“能制成规则试件的各类岩石”。直接拉伸法对试样精度要求更高，且拉伸试验过程难度较大；巴西劈裂法相对来说试样制备和试验过程均较为简单，从而得到了广泛的应用。巴西劈裂法的理论依据[6]是在弹性力学中，半无限体上作用着一集中荷载的布辛奈斯克解。但在实际使用过程中，人们往往忽略了巴西劈裂法的理论依据，盲目扩大其适用范围，从而造成测定的岩体“抗拉强度”并非正确，并且很少有人怀疑其结果的可靠性。本文结合前人的理论、试验成果，分析了巴西圆盘劈裂法的适用条件，并且根据直接拉伸法的理论分析，提出了改进性建议。

1 巴西劈裂法的分析

1.1 巴西劈裂法理论依据

巴西圆盘劈裂法所计算的是圆盘在对称、压缩的线荷载作用下的应力解析解[8]。在二十世纪早期，前苏联学者Н.И.Мусхелишьил[9]基于平面应力问题的弹性力学假定，采用复变函数的方法推导出圆盘内任意一点的应力解析解：

(1)

式中：P为巴西圆盘的径向荷载；L是圆盘的厚度；D为圆盘的直径；θ1和θ2规定如图1所示。

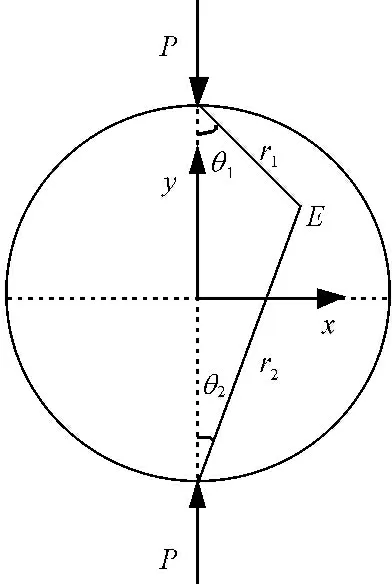
图1巴西圆盘劈裂试验受力分析图

理论上圆盘是从中心处开始破坏，因此一般也是将圆盘中心处破坏时的拉应力视为试样的抗拉强度。在圆盘中心处有r1=r2=0.5D，θ1=θ2=0，因此将其代入式(1)可得圆盘中心处的应力为：

(2)

由式(2)可知，圆盘中心处的压应力仅有拉应力的3倍，而一般岩石的抗压强度约为抗拉强度的10倍，所以认为试样的破坏为受拉破坏。在各向同性、均质岩石的劈裂试验中，试样一般也是沿着加载中心线破坏的，和理论上的破坏基本一致，这种情况下该计算方式的误差在可接受范围内。但是对于各向异性的岩石，这种传统的劈裂强度计算方法就有失准确性了。

为了解决在巴西劈裂试验中，各向异性岩石的抗拉强度计算问题，Claesson J等[10]基于横观各向同性假设，以应力平衡方程、本构方程、胡克定律、力边界条件和变形协调方程为基础，采用复变函数的方式计算出圆盘中心点的应力解析解(见图2)。

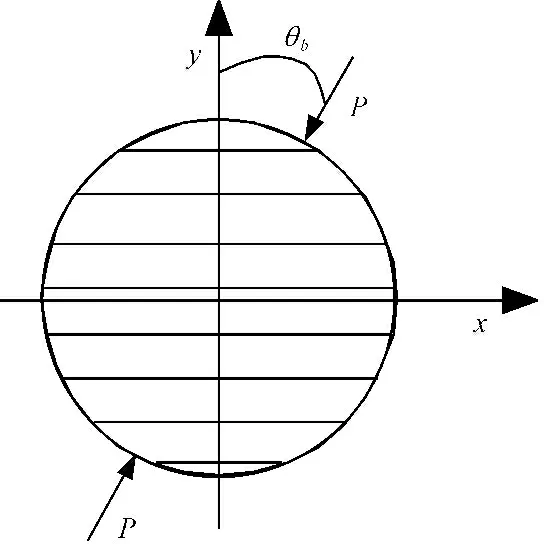
图2横观各向同性材料的巴西劈裂受力分析图

圆盘中心点(0，0)处的拉应力为：

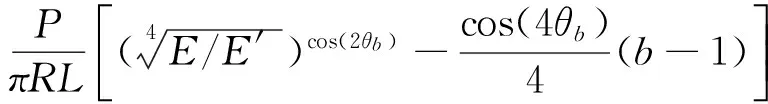
(3)

圆盘中心点(0，0)处的压应力为：

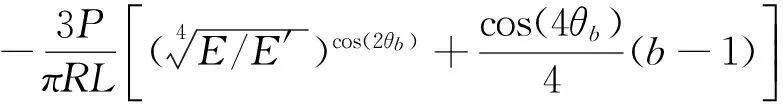
(4)

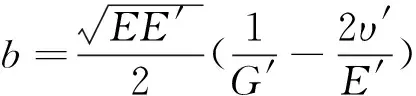
式中：P为巴西圆盘的径向荷载；L是圆盘的厚度；R为圆盘的半径；E、υ分别为x方向(和z方向)的弹性模量和泊松比；E′、υ′分别为y方向的弹性模量和泊松比；G′为xy平面(和yz平面)的剪切模量；θb(0≤θb≤π/2)为荷载施加的方向与横观各向同性面的法向之间的夹角。

1.2 层状岩体的巴西劈裂试验

在试验规程[5-7]中建议的岩石抗拉强度测定方法均为巴西圆盘劈裂试验，适用范围是能制成规则试件的各类岩石。对试件的要求均为圆柱体，直径为(50±2) mm、高径比为0.5～1.0，试件断面平面度公差小于0.5 mm，断面对于试件轴线垂直度偏差不超过0.25°。

国内外大量学者[11-17]曾对层状岩体做过巴西劈裂试验，试图测定岩体的抗拉强度。

由图3可知，只有当层理倾角和荷载方向夹角为0°和90°时，劈裂破坏面才是沿着加载直径方向穿过圆盘中心点；而其余角度下的试样并没有从圆盘中心起裂，而且劈裂破坏面也均未通过圆盘中心点，甚至严重偏离加载直径方向。因为Claesson J等[10]建立的横观各向同性岩石抗拉强度解析解，也仅仅给出了圆盘中心点具体的应力计算公式，其余位置并未具体给出，因此，采用式(3)也只能计算出层理倾角为0°和90°时(荷载施加方向与层理面法向之间的夹角)层状岩体的抗拉强度；如果其余角度下的层状岩体抗拉强度也采用该方法计算，显然不具有可信度。

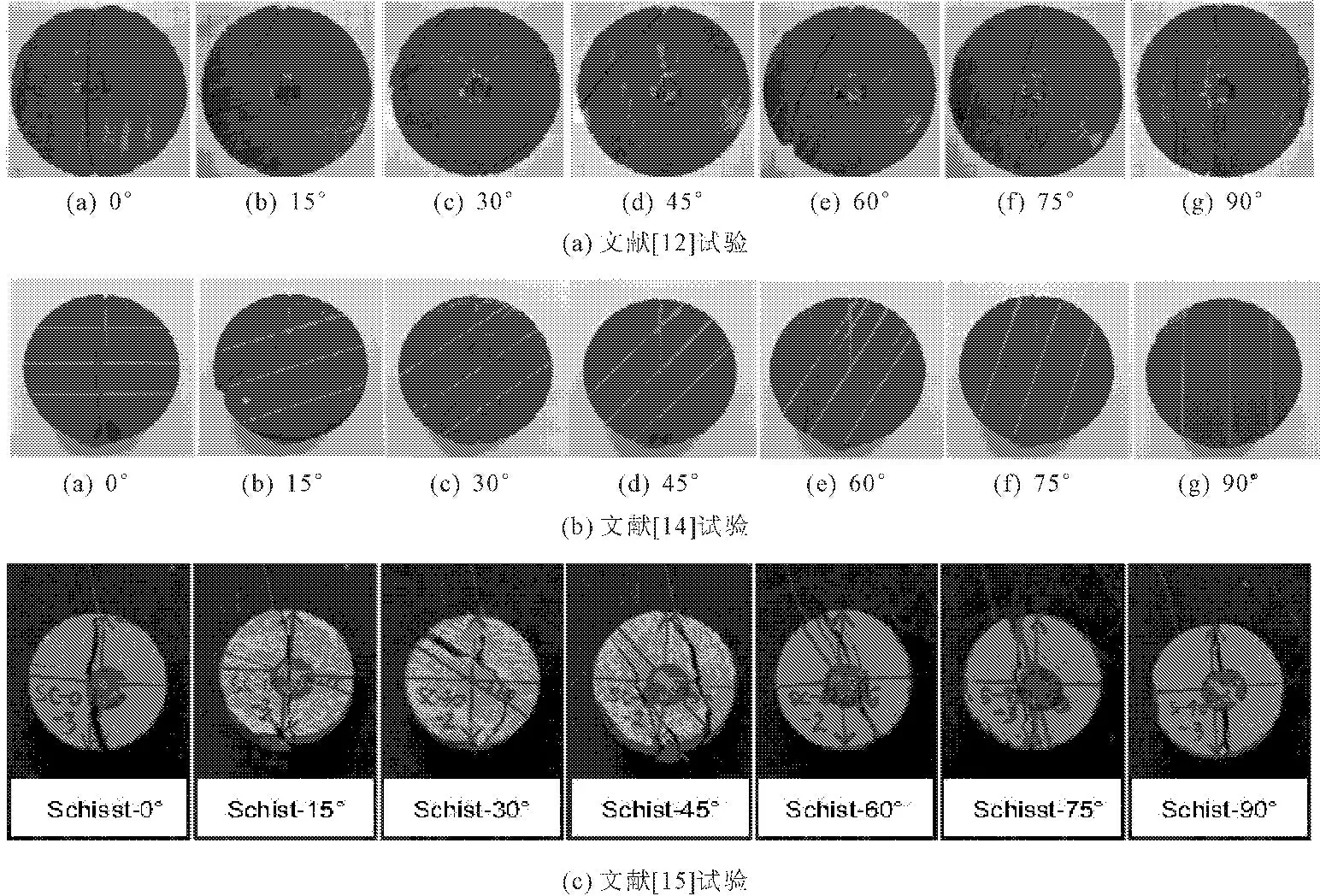
图3不同层理倾角岩体巴西劈裂试验破坏形态

通过以上分析可知，巴西圆盘劈裂试验测定岩石抗拉强度的适用范围并非试验规程上所说的“能制成规则试件的各类岩石”。采用巴西圆盘劈裂试验的结果，计算岩石抗拉强度，现有的计算理论式(2)和式(3)均有一定的适用条件，对试样的要求是：在加载直径线两侧的层理构造和岩石材料均对称分布，只有这样，圆盘试样在线性荷载作用下，内部应力才能对称分布，劈裂破坏面才能沿着加载直径方向穿过圆盘中心点。

2 直接拉伸法的分析

在理论上，直接拉伸法测定岩体抗拉强度非常简单。但由于实际操作过程中，试样严格的轴心拉伸不容易做到，在实际试验中较少使用。随着试验水平和计算机技术的提高，直接拉伸法测定岩体的抗拉强度也逐渐被重新重视起来。国内外学者也设计了很多实验方法和设备[18-23]，以使试样满足轴心受拉，并且也取得了不错的效果。

直接拉伸法常用的方式有3种：内埋式、外夹式和粘贴式，如图4所示。黄俊等[24]通过有限元数值分析，发现两端粘贴式的加载方式能够使试样内部各点应力分布比较均匀，应力集中程度也比较低。因此，本文就采用试样两端粘贴式的直接拉伸方法进行分析计算。

对层状岩体进行直接拉伸时，由于层理面的存在，导致试样内部应力并非均匀分布的。但对于试样内任意一点的应力，均可分解为沿层理方向和垂直于层理方向，如图5所示。

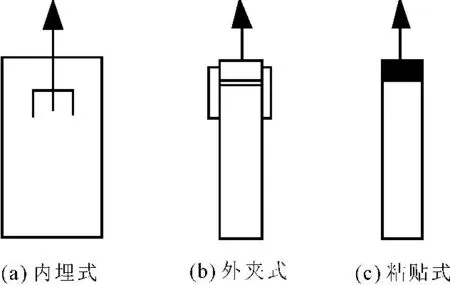
图4 直接拉伸试验简图

图5拉应力分解示意图

根据图5可知，层理面上的应力pt为：

pt=σt·cosα

(5)

可将层理面上的应力pt分解为垂直于层理面的正应力σα和沿层理面的剪应力τα：

σα=pt·cosα

(6)

τα=pt·sinα

(7)

结合式(5)、式(6)和式(7)可化简为：

(8)

(9)

因此，层状岩体试样轴向受拉破坏的条件为：

(10)

式中：σi为层理面的抗拉强度；σ0为基质的抗拉强度；ci层理面上的黏聚力；φi为层理面的内摩擦角。

层状岩体试样只要达到式(10)中的任何一个条件，就会发生相应的破坏。例如：试样仅满足σα≥σi时，为层理面上的正应力超过其抗拉强度，发生沿层理面的张拉破坏；仅满足τα≥ci+σαtanφi时，为层理面上的剪应力超过其抗剪强度，发生沿层理面的剪切破坏；仅满足σt≥σ0时，为拉应力超过基质的抗拉强度，基质发生张拉破坏。因此，试样抗拉强度和破坏位置均受岩石基质强度、层理面强度和试样内部应力分布的影响。每种破坏均有对应的试样抗拉强度(拉伸外荷载)σt，将式(8)、式(9)代入式(10)可得，与式(10)对应的试样抗拉强度为：

(11)

因此，只要事先测出层状岩体基本力学参数：σi、σ0、ci和φi，任何层理倾角下的层状岩体抗拉强度就可以根据试样的破坏形态，结合式(11)计算出来。其中，层理面的黏聚力ci和内摩擦角φi可以通过直剪试验测定，层理面的抗拉强度σi和基质的抗拉强度σ0可通过对层理倾角为0°和90°试样的巴西圆盘劈裂试验或者直接拉伸试验测定。

同时，式(11)中层状岩体试样的抗拉强度σt均可由外荷载直接计算：

(12)

式中：F为试样两端的外荷载；A为试样横截面的面积。

通过以上的理论对比分析，发现层状岩体采用直接拉伸法测定其抗拉强度会有更好的效果，结果更接近其真实的抗拉强度，同时理论解释也更加清晰明确。

3 结 论

本文通过对前人理论和试验的归纳总结，并结合直接拉伸法的理论分析，得出以下结论：

(1) 巴西圆盘劈裂试验测定岩石抗拉强度的适用范围并非试验规程上所说的“能制成规则试件的各类岩石”。巴西圆盘劈裂试验对试样的要求是：在加载直径线两侧的层理构造和岩石材料均对称分布。只有这样，圆盘试样在线性荷载作用下，内部应力才能对称分布，劈裂破坏面才会沿着加载直径方向穿过圆盘中心点，从而巴西劈裂的理论计算公式才能得到满足。

(2) 在直接拉伸试验中，当试样仅满足σα≥σi时，层理面上的正应力超过其抗拉强度，发生沿层理面的张拉破坏；仅满足τα≥ci+σαtanφi时，层理面上的剪应力超过其抗剪强度，发生沿层理面的剪切破坏；仅满足σt≥σ0时，拉应力超过基质的抗拉强度，基质发生张拉破坏；且试样的抗拉强度均为σt=F/A。

(3) 巴西圆盘劈裂试验的适用范围不能盲目地扩大，对于层状岩体的抗拉强度测定方法，建议选用直接拉伸法。

参考文献：

[1] 柳赋铮.拉伸和拉剪状态下岩石力学性质的研究[J].长江科学院院报,1996,13(3):38-42.

[2] 余贤斌,谢 强,李心一,等.直接拉伸、劈裂及单轴压缩试验下岩石的声发射特性[J].岩石力学与工程学报,2007,26(1):137-142.

[3] 张泽天,刘建锋,王 璐,等.煤的直接拉伸力学特性及声发射特征试验研究[J].煤炭学报,2013,38(6):960-965.

[4] 叶明亮,续建科,牟 宏,等.岩石抗拉强度试验方法的探讨[J].贵州工业大学学报(自然科学版),2001,30(6):19-25.

[5] 单位中铁第一勘察设计院集团有限公司.铁路工程岩石试验规程:TB 10115—2014[S].北京：中国铁道出版社,2014:54-56.

[6] 单位中交第二公路勘察设计研究院.公路工程岩石试验规程:JTG E41—2005[M].北京：人民交通出版社,2005:34-36.

[7] 中国水电顾问集团成都勘测设计研究院起草.水电水利工程岩石试验规程:SL 264—2001[M].北京：中国电力出版社,2001:28-29.

[8] 叶剑红,杨 洋,常中华,等.巴西劈裂试验应力场解析解应力函数解法[J].工程地质学报,2009,17(4):528-532.

[9] Н.И.Мусхелишьил.数学弹性力学的几个基本问题[M].赵惠元译.北京:科学出版社,1958：249-251.

[10] Claesson J, Bohloli B. Brazilian test: stress field and tensile strength of anisotropic rocks using an analytical solution[J]. International Journal of Rock Mechanics and Mining Sciences, 2002,39(8):991-1004.

[11] 刘运思,傅鹤林,饶军应,等.不同层理方位影响下板岩各向异性巴西圆盘劈裂试验研究[J].岩石力学与工程学报,2012,31(4):785-791.

[12] 叶海旺,宁卫星,雷 涛,等.层理板岩巴西劈裂破坏模式的方向效应研究[J].武汉理工大学学报,2016,38(9):91-97.

[13] 侯 鹏,高 峰,杨玉贵,等.黑色页岩巴西劈裂破坏的层理效应研究及能量分析[J].岩土工程学报,2016,38(5):930-937.

[14] 杨志鹏,何 柏,谢凌志,等.基于巴西劈裂试验的页岩强度与破坏模式研究[J].岩土力学,2015,36(12):3447-3455，3464.

[15] Cho J W, Kim H, Jeon S, et al. Deformation and strength anisotropy of Asan gneiss, Boryeong shale, and Yeoncheon schist[J]. International Journal of Rock Mechanics & Mining Sciences, 2012,50(2):158-169.

[16] 侯 鹏,高 峰,杨玉贵,等.考虑层理影响页岩巴西劈裂及声发射试验研究[J].岩土力学,2016,37(6):1603-1612.

[17] 刘胜利,陈善雄,余 飞,等.绿泥石片岩各向异性特性研究[J].岩土力学,2012,33(12):3616-3623.

[18] 袁瑞甫,侯志强.岩石试样直接拉伸力学性能及声发射活动分析[J].河南理工大学学报(自然科学版),2017,36(1):122-128.

[19] Liu J, Xu J, Xie H. Spring supported lower clamper for direct tensile test: US7624647[P]. 2009.

[20] 赵宝云,刘东燕,薛凯喜.重庆红砂岩单轴直接拉伸特性试验研究[J].工程勘察,2011,39(4):9-12.

[21] 梁正召,唐春安,张永彬,等.岩石直接拉伸破坏过程及其分形特征的三维数值模拟研究[J].岩石力学与工程学报,2008,27(7):1402-1410.

[22] 陶纪南.岩石轴向拉伸与劈裂法试验结果的比较分析[J].金属矿山,1995(3):28-31.

[23] 曾召田,徐云山,唐双慧,等.武鸣红黏土轴向压裂与单轴拉伸抗拉强度试验对比研究[J].水利与建筑工程学报,2016,14(2):25-29.

[24] 黄 俊,姜弘道.混凝土单轴直接拉伸受力分析[J].河海大学学报(自然科学版),2006,34(3):306-310.