平面钢闸门流固耦合分析与优化设计

常 富，纪 伟

(1.水利部 长春机械研究所， 吉林 长春 130012； 2.吉林省中部城市供水股份有限公司， 吉林 长春 130000)

某引水工程取水口工作闸门，设计引水流量为38.0 m3/s，孔口尺寸为7.0 m×7.0 m(高×宽)，设计水头为36.9 m，底坎高程为231.6 m，检修平台高程272.0 m。闸门为潜孔式平板滚动钢闸门，操作方式为动水启闭。由于该闸门设计泄流量较大、隧洞充水时间长并且有局部开启控制泄流的要求，致使闸门下部水位变化大，水流运动形态复杂。为防止闸门局部开启时产生强烈振动，甚至诱发共振[1]，有必要对闸门进行物理模型试验研究与数值模拟计算预测，保证闸门在运行中的安全可靠性。鉴此，本文首先运用有限元软件对闸门进行流固耦合分析，求出闸门的湿模态[2]。通过闸门水动力模型测得闸门相应部位的脉动压力值，得到作用在闸门门体上脉动压力的主频，预测出闸门有产生共振的风险[3-4]。对闸门进行优化设计，使优化后闸门的自振频率远离脉动水流高能区，达到优化设计的目的。

1 平面钢闸门流固耦合分析

1.1 流固耦合理论

考虑流体质量对闸门的影响，在结构坐标系中离散化后的结构动力平衡方程为[5-7]

(1)

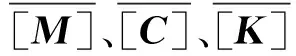
(2)

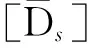
(3)

记作：

{Fs}=-[Mg]{D}

(4)

代入移项后得到：

(5)

当考虑结构的自由振动时，荷载向量为0。同时大量的实例证明，结构的阻尼对结构的自振频率和振型影响很小，加之不考虑结构阻尼，使结构自振特性计算的工作量大为减少。因此，可以略去阻尼的影响来确定系统的自振频率和振型[8]。则式(5)变为：

(6)

1.2 平面钢闸门自振特性分析

1.2.1 计算模型

该平面钢闸门包括八根工字形主梁、一根底梁和两边两根箱梁组成。闸门的主梁布置见图1和图2。闸门高7 570 mm，宽8 400 mm，面板厚20 mm。平板闸门属于空间薄壁结构体系[9-10]，文中采用实体单元Solid 45模拟该工作闸门的结构体系。无限水域的长度模拟取闸门高度的10倍，水体单元采用Fluid 30单元。控制闸门门体结构划分单元长度为50 mm，水体结构单元长度为300 mm，采用空间四面体网格，最终离散总单元2 400 579个，节点553 398个。其中，门体结构Solid 45单元共1 063 216个；水体单元1 337 363个单元。闸门与水体数值模型见图3所示。其中，垂直水流方向为X轴，顺水流方向为Z轴，闸门高度方向为Y轴[11-12]。

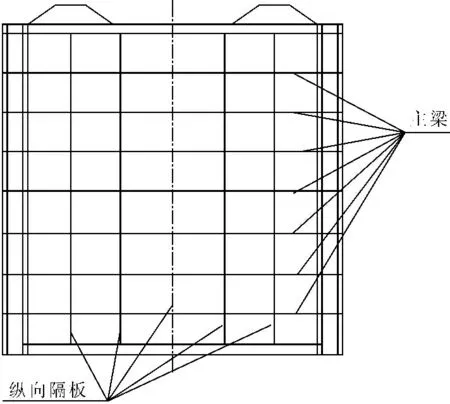
图1 平面闸门简图

图2 平面闸门主梁布置图

图3闸门、水体有限元模型

1.2.2 相关参数

闸门结构材质Q345，闸门总重104.00 t，其中闸门体自重60.42 t，闸门配重块43.58 t。弹性模量E=2.1×105MPa；泊松比μ=0.3；质量密度ρ=7 800 kg/m3；重力加速度g=9.8 N/kg；水体密度1 000 kg/m3，声音在水中传播速度V=1 460 m/s。

1.2.3 边界条件

采用连杆约束限制闸门的位移。即在闸门主轮与闸门槽相交处施加Z轴方向的约束，在闸门顶端吊耳处施加沿Y轴方向约束。闸门门体与水体交界面设置为耦合面[13]。

完成以上各步骤后采用直接耦合的方法对闸门进行模态求解计算。在ANSYS中，采用非对称(Unsysmmetric)法来提取模态结果。

1.2.4 计算结果分析

由于闸门随着开度的增大，闸门与水体接触面积逐渐减小，所受水体附加质量效应的影响也逐渐减小，闸门的自振频率会随之逐渐增大。故本文只对闸门在关闭状态下，分析闸门的干、湿模态[14-15]。闸门在关闭状态下，前10阶干模态和湿模态见表1。

从表1中数据可以看出，闸门的低阶干模态为14.9 Hz，低阶湿模态为9.5 Hz。

表1 闸门前10阶模态

2 平面钢闸门水动力模型试验

该试验中，闸门的水动力模型采用有机玻璃制作，模型比尺Lr=12，闸门原型尺寸及模型尺寸见表2，主要测量闸门底缘上的脉动压力荷载值。闸门模型见图4。

表2 闸门原型和模型尺寸对比表

图4闸门模型

本文主要分析闸门底缘脉动压力值对闸门振动的影响，故脉动压力测点均集中在闸门底缘。闸门底缘脉动压力测点布置见图5，其中闸门面板布置3个测点，分别为测点P1、测点P3、测点P4；闸门底缘布置1个测点P2，在闸门底部两根主梁的腹板和后翼缘布置4个测点，在闸门底梁斜翼缘布置1个测点。

从闸门的水力学模型试验中得到了闸门底缘在不同开度下脉动压力时程曲线及功率谱密度曲线，如图6～图10所示。

从功率谱密度曲线中得出该闸门在不同开度下的存在四个主要频率点：分别为0.90 Hz、4.86 Hz、10.74 Hz和17.60 Hz。和闸门的自振频率对比发现，闸门的低阶模态与水流脉动主频相近，有产生共振的风险，需要对闸门进行优化设计，提高闸门的低阶振动频率。

3 闸门的优化设计

3.1 优化基本原则

在保证闸门整体质量不变的情况下，提高闸门的刚度。具体做法为取消闸门的配重块，将配重块的重量分配到闸门门体各构件上；闸门主梁改为变截面式工字型主梁，提高闸门面板的厚度以及主梁腹板高度、厚度，以达到提高刚度的目的。

3.2 优化后闸门的数值模型

依据优化基本原则，闸门面板厚度最终变为30 mm，主梁腹板厚度最终变为40 mm，横隔板厚度最终变为40 mm，主梁形式改为变截面式工字形主梁，具体尺寸见图11。为进一步提高闸门刚度，增加水平次梁，水平次梁为40 a型号槽钢。将主梁间后翼缘进行连接封闭变成面板。运用该方法、措施进行优化后的闸门自重为104.52 t，与原设计重量基本相同。相关尺寸及结构布置如图12、图13所示。

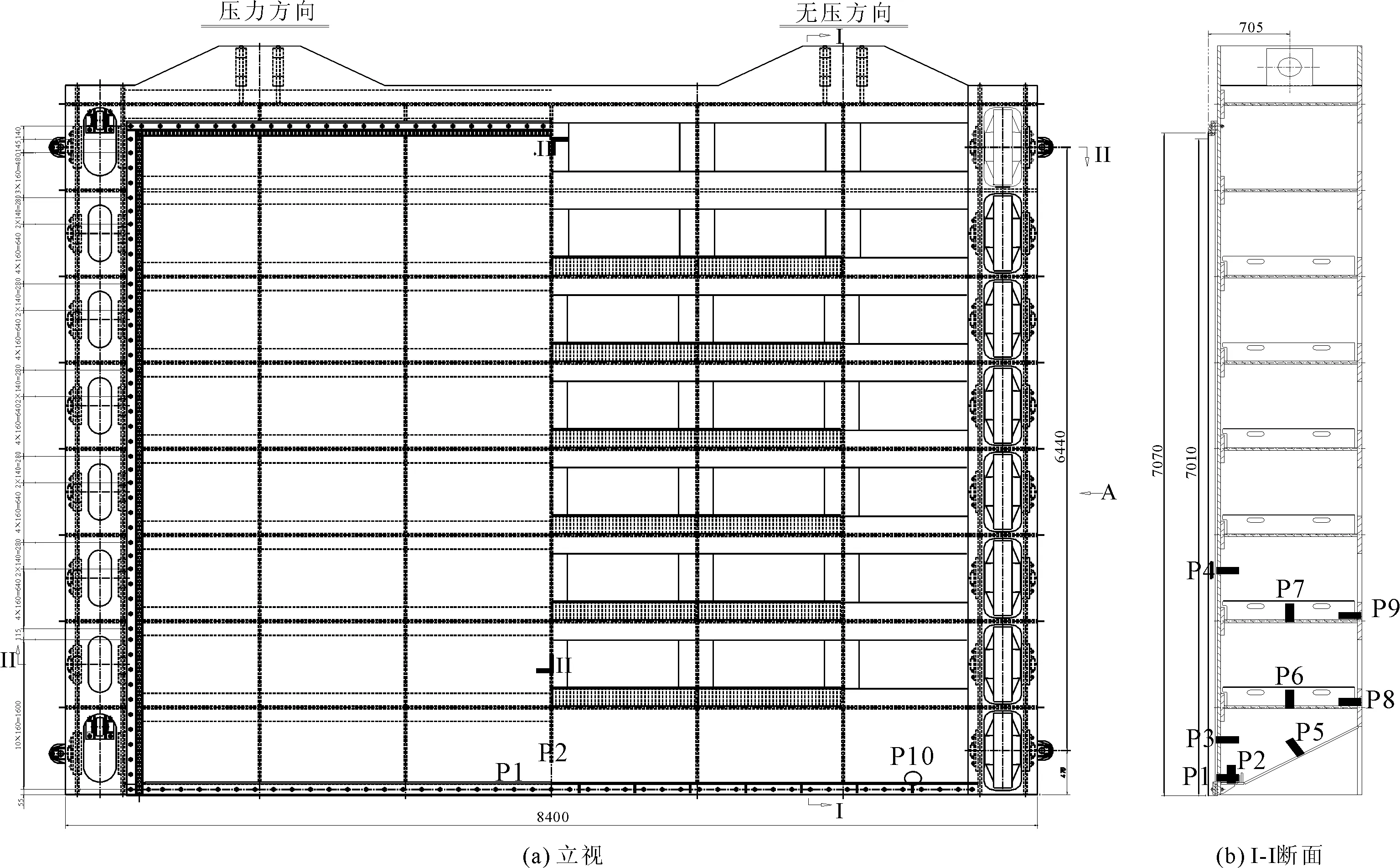
图5闸门脉动压力测点布置图

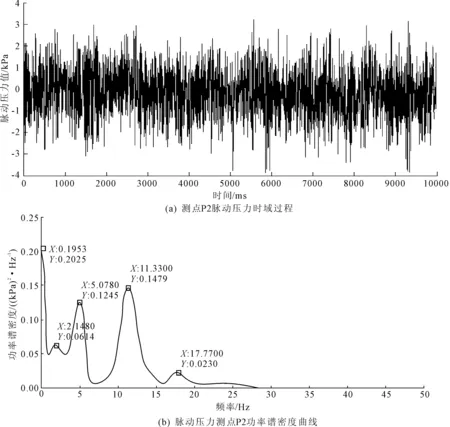
图6 闸门在0.1开度时底缘脉动压力时域和频域过程曲线

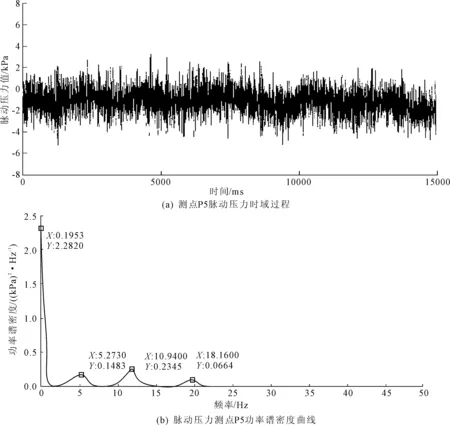
图7 闸门在0.2开度时底缘脉动压力时域和频域过程曲线

3.3 优化后计算结果

分析优化后闸门前10阶干湿模态如表3所示。

从表3中数据可以看出，闸门的低阶干湿模态均有所提高，并已经基本远离水流脉动的高能区，达到优化设计的目的。

表3 优化后闸门前10阶干湿模态

4 结 论

(1) 通过对该工程工作门进行自振特性分析，得到该闸门的低阶干模态为14.90 Hz，湿模态9.50Hz。由闸门的水力学试验可知，闸门在不同开度下运行主要存在四个主要频率点：分别为0.90 Hz、4.86 Hz、10.74 Hz和17.60 Hz。闸门的自振动频率与水流脉动主频相近，有产生共振的风险。

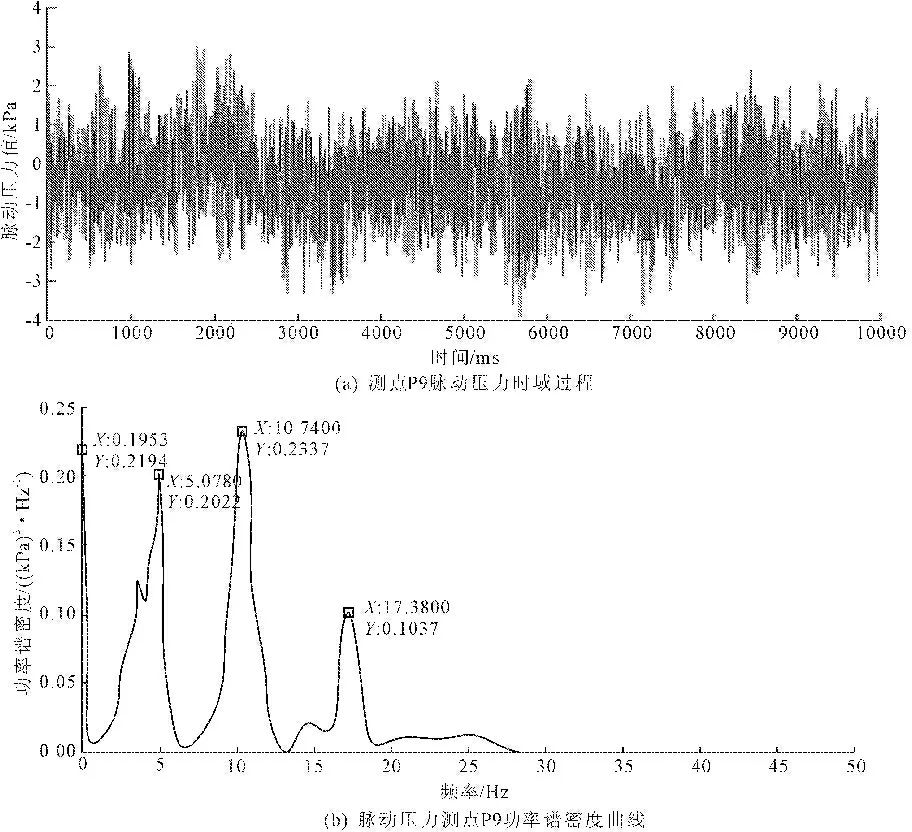
图8闸门在0.3开度时底缘脉动压力时域和频域过程曲线

图9闸门在0.4开度时底缘脉动压力时域和频域过程曲线

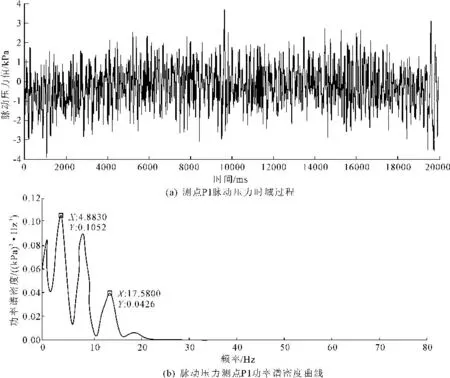
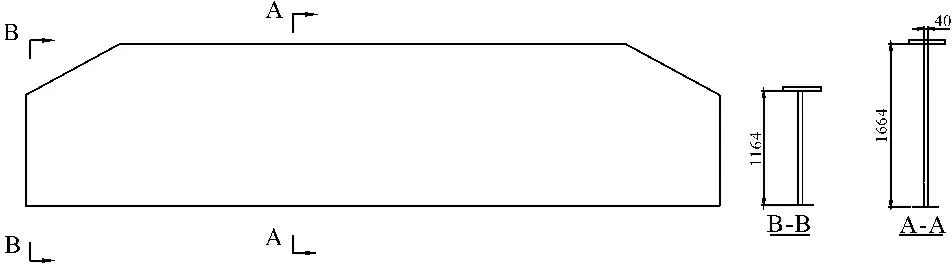
图10 闸门0.5开度时底缘脉动压力时域和频域过程曲线

图11闸门优化后主梁平面图

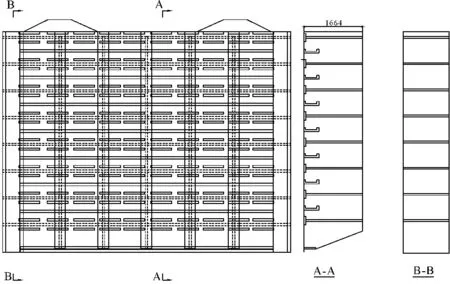
图12 闸门优化后整体模型

图13闸门优化后立体模型

(2) 通过对闸门进行优化设计，使得优化后闸门的低阶干模态为27.00 Hz，湿模态为19.50 Hz，已基本远离水流脉动高能区，达到优化目的。

参考文献：

[1] 祝智卿,朱召泉.中高水头船闸三角门流固耦合动力特性分析[J].水运工程,2013(6):119-122.

[2] 杨明镜.露顶式钢闸门地震动水压力研究[D].杨凌：西北农林科技大学,2013.

[3] 赵兰浩,骆 鹏.大型水工弧形钢闸门流激振动物理模型—数值模型计算分析[J].水电能源科学,2017,35(12):173-177.

[4] 李 昊.水力自动滚筒闸门振动特性的试验研究及数值模拟[D].呼和浩特：内蒙古农业大学,2013.

[5] 胡剑杰,胡友安,王 煦.基于ANSYS的弧面三角闸门自振特性研究[J].三峡大学学报(自然科学版),2014,36(6):24-27.

[6] 赵 营.双悬臂钢叠梁闸门静动力学有限元分析[D].邯郸：河北工程大学,2017.

[7] 杨婷婷.淹没条件下平面直升闸门流固耦合振动研究[D].昆明：昆明理工大学,2016.

[8] 鲍秋慧,胡兆荣,孙蓬勃.升卧式卧倒闸门的自振特性[J].人民黄河,2013,35(2):114-115，119.

[9] 赵春龙,王正中,王明疆,等.深孔平面钢闸门挡水布置形式的受力特性比较[J].水力发电学报,2018,37(1):11-20.

[10] 张 凡,巫世晶,孟凡刚,等.基于CEL理论的弧形闸门流固耦合的数值模拟[J].水电能源科学,2016,34(3):189-191，27.

[11] 朱剑军.基于点源(汇)附加质量法的平面闸门流固耦合振动特性研究[D].昆明：昆明理工大学,2014.

[12] 杨 超.底横轴翻转闸门静力学与动力学特性分析[D].合肥：安徽建筑大学,2017.

[13] 刘鹏鹏,郑圣义.某箱型结构弧形闸门自振特性的有限元分析[J].机械制造与自动化,2013,42(4):172-174.

[14] 连子怡.三支臂弧形钢闸门静动力特性研究[D].武汉：武汉大学,2017.

[15] 王嘉宝.考虑流激振动的水工弧形钢闸门数值模型研究[D].郑州：华北水利水电大学,2017.