基于面状几何基元的特征自动提取技术
2018-05-09甄宗坤蔡东健
甄宗坤,蔡东健
(苏州工业园区测绘地理信息有限公司, 江苏 苏州 215027)
三维激光点云中噪声、外点和数据缺失的存在,使得寻找一种高效、鲁棒的点云数据处理方法成为当前学术界和工业界共同关注的热点之一[1]。另外,除了根据局部分布特点对点云进行处理之外,例如点云特征保持和鲁棒的法向量估计与重定向方法,如何从点云中提取出能够反映其全局特征或结构性特征的信息,再借助这些信息对点云进行处理,是另外一种提高特征提取鲁棒性的思路。随着点云快速模型化技术的发展,传统的由点到线,再到面和模型的解决方案被彻底打破,全新的面片检测技术[2],快速的面片生长、融合方法,为点云快速模型化提供了便利,这也为由模型到轮廓的逆向解决方案提供了技术基础。
基于面状几何基元的特征自动提取技术,首先需要对点云进行初始法向量估计,并对所得到法向量进行重新定向,然后使用主元分析法[3],寻找单体建筑点云的主成分法向量,每个主成分法向量代表单体的一个面或一组平行面,对于平行面可通过位置属性进一步筛选,以获取建筑每个特征面的主成分法向量和归属点云,进而根据主成分法向量和点云,建立特征面片集,面片之间采用双向索引连接法建立几何拓扑,实现建筑立面几何重建,最后,通过平面裁切建筑立面的几何模型,获取的切痕即是建筑物的平面特征线。这种全新的点云平面轮廓线生成算法从根本上解决了点云空洞和特征线局部锯齿化的问题,实验表明,该算法提取平面特征线准确、完整,且自动化程度高[4]。
1 算法描述
1.1 法向量估计
(1) 基于核密度估计的局部切平面法向量。对于点云中的每个点p,搜索与其最近的k邻域,邻域范围足够大,在此邻域内,随机选择三个不共线的点初始化一个平面,对每一个候选平面θ,计算邻域中的点到它的距离ri,θ,然后选择出核函数K及其宽带h,此时残差μ对应的核密度fθ可以定义为[5]:
(1)
式中:ω为一个归一化因子,其值为邻域中所有点在θ上的投影所占的面积。
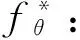
(2)
法向量局部平面拟合法,具有低通的特性,使得尖锐特征的法向量估计并不明显。而且这种方法计算出的法向量具有二义性,即只是得到了法向量所在的直线,却没有明确的方向,故仍须对法向量进行重定向[6]。
(2) 法向量重定向。假定点云足够稠密且表面光滑的前提下,相邻两数据点的法向量是接近平行的,即nj·ni≈±1。若nj·ni≈1,则法向量同向;若nj·ni≈-1,则法向量异向,须将其中一个反转过来。为此,以点云中的每个点为节点,点之间的相邻关系为边,相邻点法向量的内积为边的代价构造一个无向图。采用改进的最小生成树的方法对法向量进行重定向。
图1中实心箭头表示原始的法向量估计,空心箭头表示部分反向法向量估计重定向后的方向。初始法向量估计与重定向的目的主要是要获得与物体表面具有一致性的外向法向量。
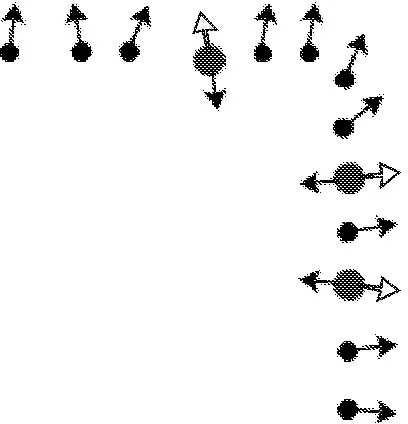
图1法向量重定向
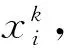
(3)
1.2 主元分析构建面状几何基元
对于单体化的建筑,每个立面的法向量方向具有高度的一致性,通过主元分析法获取该立面几何中一致性的法向量,此法向量代表着一个特征面或一组平行面的主成分方向[9](如图2所示),主成分方向1-1和4-1代表着一个独立的特征面,而主成分方向2-1、2-2和3-1、3-2代表着一组平行的特征面。对于平行面的分离问题可利用某一主成分法向量方向和建筑物内部中心点构建的局部坐标系,通过计算平行面距坐标原点的距离可实现平行面的自动分离。平行面分离之后,对于单体建筑的每一个立面的点云和对应的主成分法向量均一一确定,结合采样一致性算法RANSAC和最小二乘平面拟合即可建立单体建筑的面状几何基元[10]。
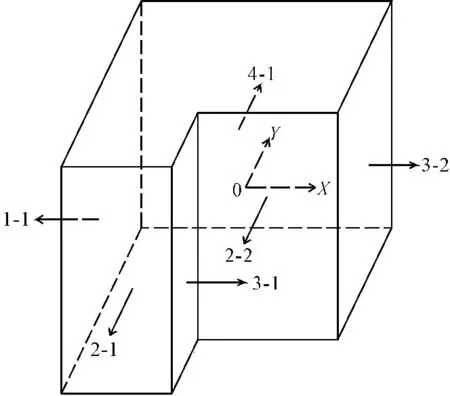
图2主成分法向量
1.3 面状几何基元双向索引连通
对确定的具有实际代表性的面状几何基元,只需要确定相互的几何拓扑,即可完成建筑立面的几何重建。面状几何基元的拓扑关系采用双向索引连通法建立,特征面基元向左、右两个方向索引相邻特征面,再通过法矢变化和几何拓扑约束,寻找最优的相邻特征面片,建立特征面片的空间索引,进而生成具有索引机制的建筑物立面模型。图3是按面片双向索引建立特征线的的原理图,通过主元分析法识别出的,且具有实际代表性的特征面基元A、B沿左向、右向索引,构造出立面模型的特征线L1[11-12]。
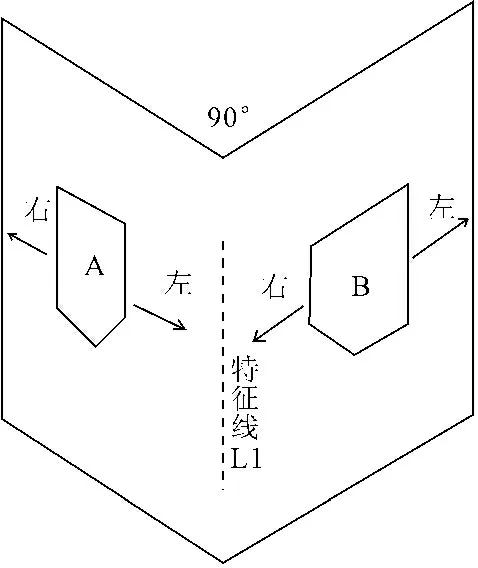
图3面基元双向索引连通
1.4 平面裁切
利用平面裁切技术构建平面轮廓线需满足两个基本条件:(1) 特征面基元建立了正确的空间索引关系,几何拓扑与实际相吻合;(2) 立面模型的特征线集索引无误。平面裁切线与特征面片和特征线集相交形成裁切点,裁切点按照索引规则连接成线段,线段集按最小面积规则分别构建成切痕特征线[13-14]。图4是按照面状基元检测技术构建平面特征线的示意图;图4(a)是三维点云和特征面片;图4(b)是平面裁切面与特征面片的切痕。
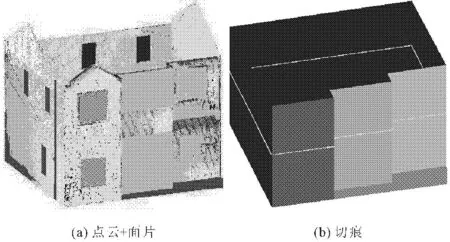
图4面状几何基元检测构建特征线示意图
2 实例验证
对于常见的直角单体建筑,其立面的主成分法向量为4个,但多数情况下会包含一个或多个平行面。如图5所示,主方向1和主方向2含有一个立面,而主方向3和主方向4则包含多个平行面,利用同一立面或平行面具有相同或相似法向量信息的特征,通过主元分析法统计出4个主成分法向量,然后在单体建筑中心设立以主方向3为X轴、以主方向2为Y轴的局部坐标系,在局部坐标系中,具有相同主方向的平行面在位置上有着明显的差异,使用该特征将平行面快速分离。利用主元分析法获取单体建筑的主成分法向量,并进一步分离平行面的结果如图6和表1所示。

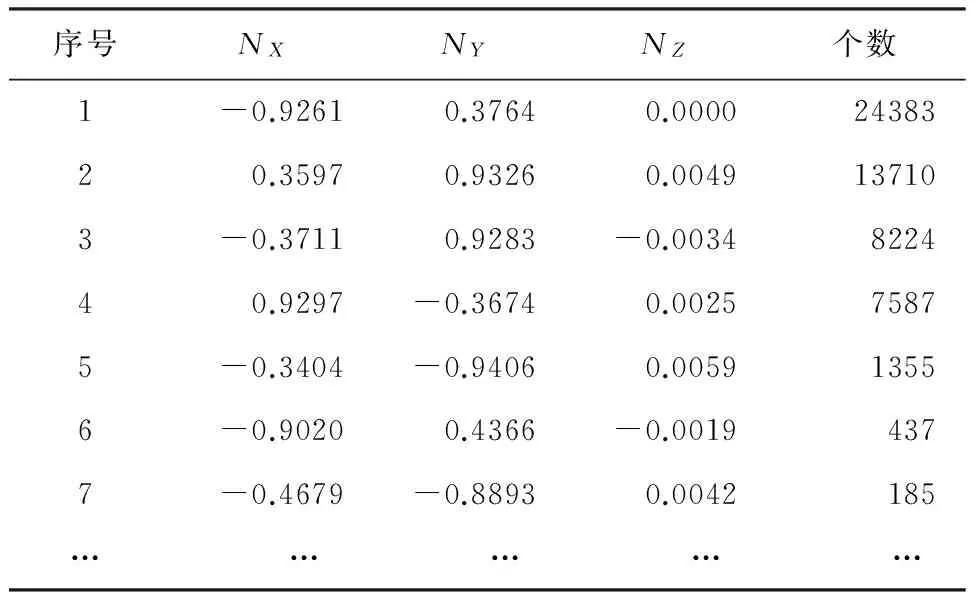
图5 单体建筑立面的四个主成分方向
图6(a)和表1为利用主元分析法获取的单体建筑主成分法向量的示意图和分析表。从图6(a)和表1中,可以明显识别出此单体建筑的4个主成分法向量,主成分法向量之间表现出以下特征:(1) 主方向1和主方向3、主方向2和主方向4是相互平行,且方向相反;(2) 主方向1、主方向3与主方向2、主方向4之间互相垂直。这一法向量特征与该单体建筑的实际情况十分吻合。图6(b)为分离平行面而重新定义的局部坐标系示意图,从图6(b)中可以看出,在重新定义的局部坐标系中,可以非常简单地将具有相同主成分方向(主方向3)的平行面通过位置属性进行快速分离。至此,单体建筑的每一个立面的点云和对应的主成分法向量均一一确定,再结合RANSAC和最小二乘平面拟合即可建立单体建筑的面状几何基元。
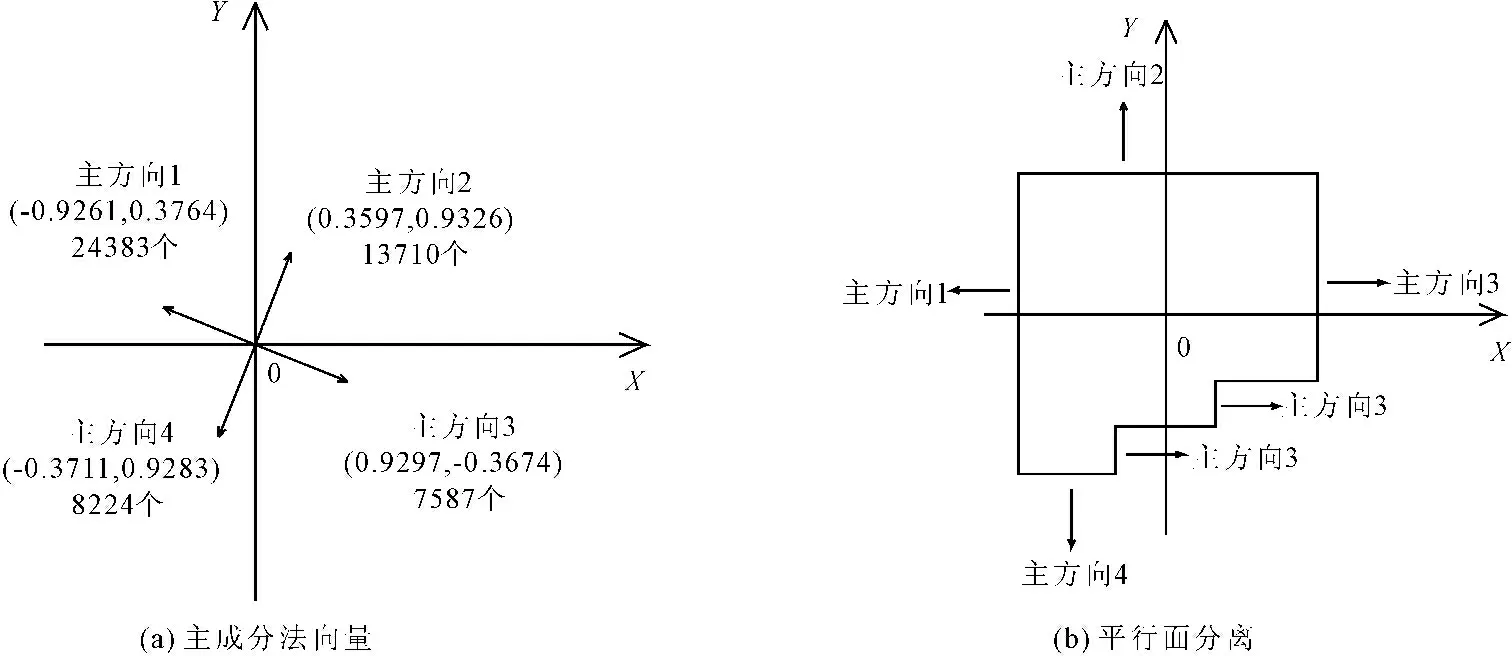
图6单体建筑的主元分析
为了进一步测试算法的有效性、正确性和可靠性,测试选择了公司在某农村建设用地的实际项目,采用Leica Pegsus Backpag背包式三维激光扫描仪设备获取的建筑点云数据,测区包含宗地约83户,共约200个房屋,房屋以两层建筑为主,建筑多有柱廊、阳台,主房门窗个数一般多于5个,且部分有异形结构。点云采集过程中,没有刻意对局部进行扫描,具有一般性,包含大量的非目标点,同时局部点云缺失和噪点情况也较为普遍。测试中使用传统测量方式采集了该区域80个特征点,将采集的特征点坐标与本文方法绘制的平面特征线角点进行精度对比,对比的情况和结果如图7和表2、表3所示。
图7(a)为该区域的三维激光点云,点云已作初步的预处理,图7(b)为本文算法生成的平面特征线,图7(c)为平面轮廓线符号化后的成果图。表2为点云平面轮廓线特征点的精度情况表,表3为点云平面轮廓线特征点的精度统计表,经计算,X方向的中误差为±2.3 cm,Y方向中误差为±1.8 cm,平面位置中误差为±2.9 cm。经过对比,本文所提出的新的点云平面特征线生成算法在精度、准确度、适用性和可靠性上均有着良好的表现。
3 结 论
在针对具有大数据特征的点云处理算法中,基于点云几何特征的表面重建算法是近年来研究的热点,然而其在处理包含不规则噪点、点云空洞和几何缺失等问题点云时,往往呈现出局部的锯齿和表面中断现象,更为严重的是在处理具有实际意义的尖锐特征点云时,会绘制成连续的折线,出现不同程度的失真,精度和准确度更是难以保障[15]。
基于面状几何基元的特征自动提取技术,不依赖于点云的密度、几何特征和离散情况,彻底改变了传统的由点到线、由线到面和模型的点云处理模式。对于单体化建筑点云采用法向量主元分析和几何结构筛选很好地解决了面状几何基元检测和平行面自动分离的问题,保证了由点到面、由面裁切成线的方案实施,从根本上解决了因点云质量引起的表面局部锯齿和中断的难题。面状基元的双向索引连通和平面特征线裁切技术,可以快速、准确地实现点云特征线线的自动生成,可以很好地复原具有实际意义的平面特征,同时具有一定的抑噪能力。
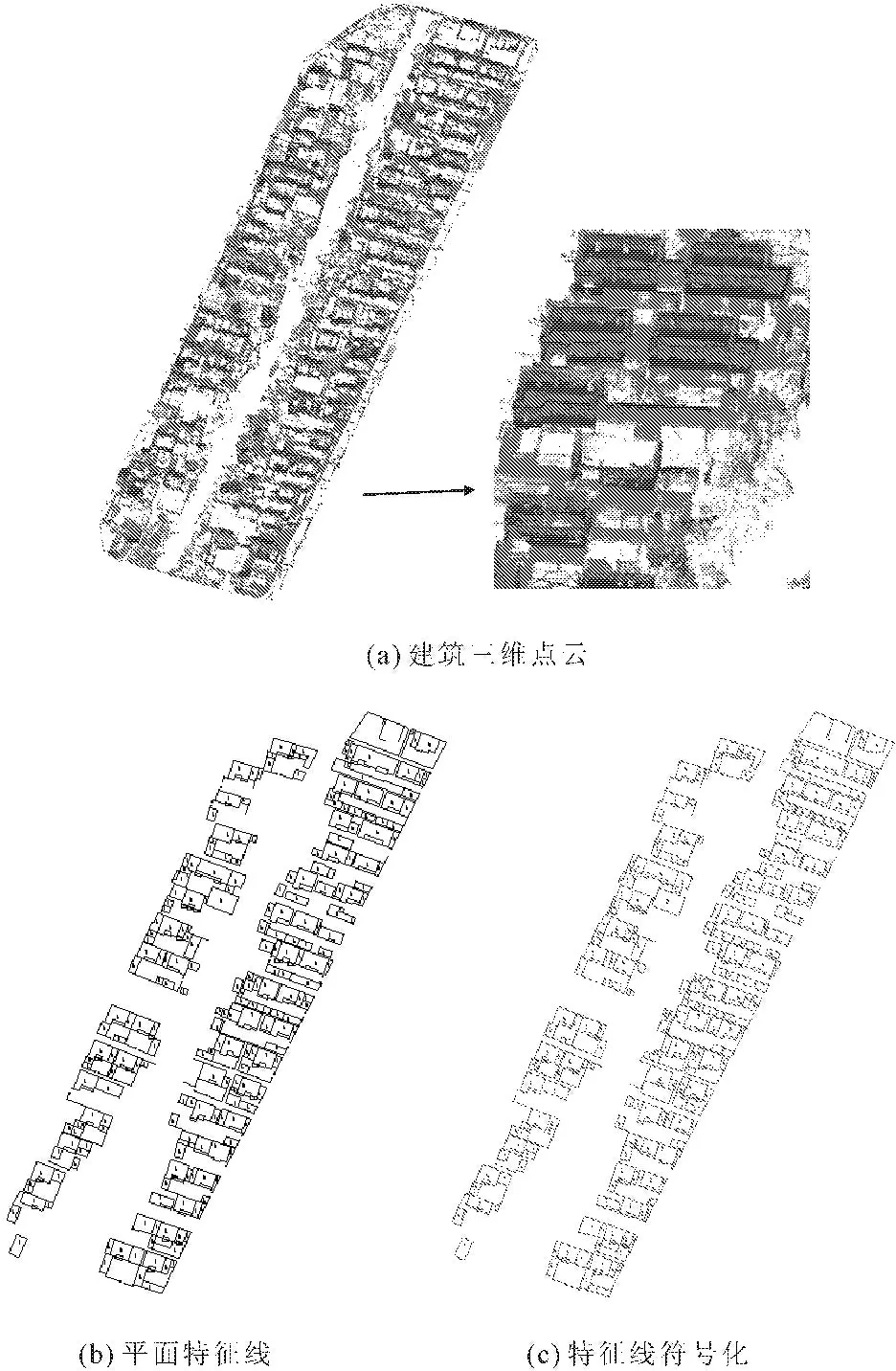
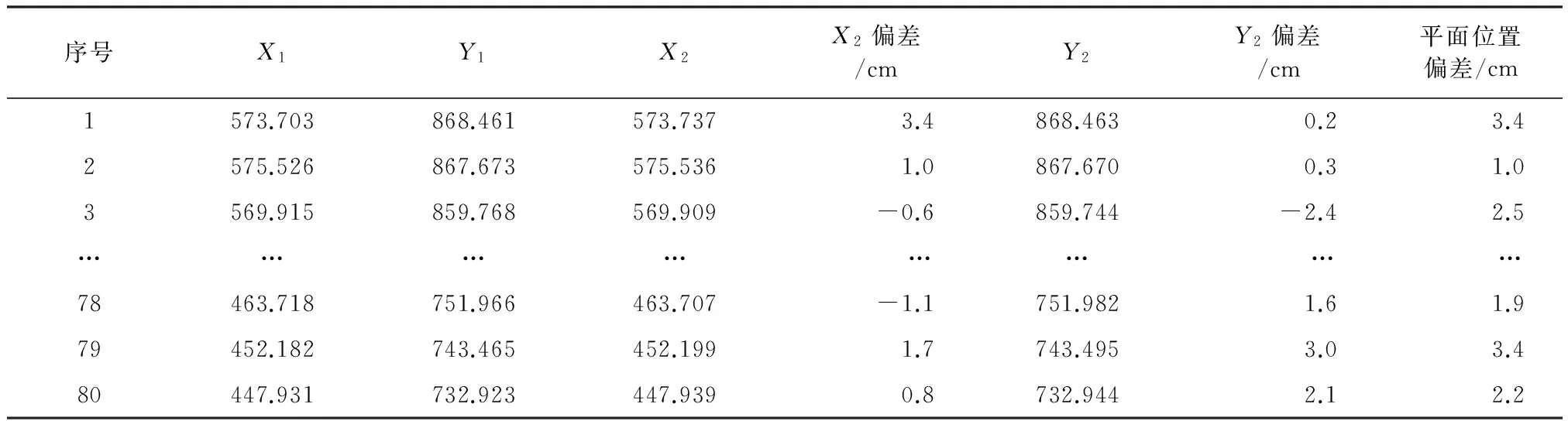
图7 基于面状几何基元的平面特征线
注:1代表平面特征点;2代表基于面状几何基元的平面特征点。

表3 平面特征线检查精度统计表
注:M=5 cm。
参考文献:
[1] 刘尚蔚,朱小超,张永光,等.多片点云数据拼接处理技术的研究[J].水利与建筑工程学报,2014,12(1):121-124.
[2] 钱鹏鹏,郑德华.一种新的扫描点云自动配准方法[J].水利与建筑工程学报,2013,11(3):162-164,172.
[3] 严剑锋,邓喀中.基于PCA和Delaunay剖分点云配准算法研究[J].现代测绘,2016,39(1):29-32.
[4] 吴杭彬,刘 春.激光扫描数据的等值线分层提取和多细节表达[J].同济大学学报(自然科学版),2009,37(2):267-271.
[5] Oztireli C, Guennebaud G, Gross M. Feature preserving point set surfaces based on non-linear kernel regression[C]//Computer Graphics Forum, 2009:493-501.
[6] 康志忠,王微微,李 珍.多源数据融合的三维点云特征面分割和拟合一体化方法[J].武汉大学学报(信息科学版),2013,38(11):1317-1321.
[7] Cheng F, Fan F, Lai S, et al. Progressive interpolation using loop subdivision surfaces[C]//Proc of the 5th Int Conf on Advances in Geometric Modeling and Processing. Berlin:Springer, 2008:526-533.
[8] 李 宝.三维点云的鲁棒处理技术研究[D].长沙:国防科学技术大学研究生院,2011:83-87.
[9] 张 坤.基于三维激光扫描的点云数据逆向重建算法研究[D].秦皇岛:燕山大学,2016.
[10] 秦家鑫,万幼川,何培培,等.一种建筑物点云轮廓线的自动提取算法[J].遥感信息,2015,30(4):03-07,13.
[11] 程效军,贾东峰,刘燕萍.海量点云数据轮廓线的快速生成算法[J].同济大学学报(自然科学版),2012,40(10):1559-1563.
[12] 崔婷婷.结合车载点云和全景影像的建筑物立面重建[D].武汉:武汉大学,2015.
[13] 闫吉星.建筑物LiDAR点云三维重建的全局优化方法[D].武汉:武汉大学,2015.
[14] 周保兴.基于三维激光扫描技术的建筑物变形监测方法研究[D].南京:河海大学,2013:93-114.
[15] 沈超慧,黄石生,胡事民.城市建筑点云的自适应分割方法[J].计算机辅助设计与图形学学报,2012,24(2):149-151.
