基于空间组合式单元模型的表面求交算法

汪基伟，付 宇，王亚奖



基于空间组合式单元模型的表面求交算法

汪基伟1，付 宇1，王亚奖2

(1. 河海大学土木与交通学院，江苏 南京 210098；2. 泉州市审计局，福建 泉州 362000)

在空间埋置组合式单元模型中，钢筋单元可埋置于混凝土单元任何位置，混凝土单元网格剖分不受钢筋位置的限制，方便实用，但需确定钢筋单元两端在混凝土单元表面的位置坐标。因此，求解钢筋线与混凝土单元表面的交点坐标是应用该单元模型的前提，现有的求解方法只适用于混凝土单元表面是平面的情况。为此，提出了牛顿迭代法和分块解析法两种处理方法，能求解钢筋线与混凝土单元表面为任何形状时的交点坐标，增强了该模型的适用性。通过算例验证了这两种方法的正确性。从适用性而言，分块解析法要优于牛顿迭代法。

钢筋混凝土有限元；单元模型；前处理；曲面表面

现有钢筋混凝土结构有限元模型[1]中，分离式单元模型采用块体单元模拟混凝土，杆单元模拟钢筋[2-3]，杆单元必须在混凝土单元边界上，结构配筋复杂时网格剖分困难，有时甚至难以实现。整体式单元模型[4]将钢筋弥散于整个单元中，利用单元参数(如配筋率)求得考虑钢筋作用后的单元折算弹性模量，再以折算弹性模量求单元刚度矩阵，以考虑钢筋对单元刚度矩阵的贡献，该模型无法考虑钢筋的具体位置，也不能求出钢筋应力分布。埋置式单元模型[5-6]将钢筋埋置于混凝土单元内部，网格剖分方便且能求得钢筋应力，单元刚度为混凝土单元刚度与钢筋单元刚度之和，其中混凝土单元刚度矩阵仍采用等参单元的刚度矩阵，而钢筋单元刚度矩阵则利用混凝土与钢筋应变相同的原则得到。文献[7]和[8]分别推导出了二维和三维埋置式单元模型，钢筋单元刚度矩阵s和应力矩阵s表达式为

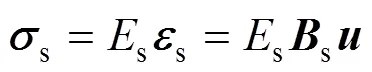
其中，s为钢筋单元应变矩阵；s为钢筋弹性模量；s为钢筋截面面积；d为杆单元任意点所在的微分段；为单元结点位移列阵。

由式(1)、(2)可知，埋置式单元模型必须得到钢筋线与混凝土单元表面的交点坐标。文献[8]虽给出了求解方法，但该方法假定单元表面为平面，不适用于单元表面为曲面的情况。在钢筋混凝土有限元网格剖分中，希望形成表面为平面的规则单元，但结构形状复杂时难以做到，剖分后必然会出现表面为曲面的单元，现有方法无法应用。曲面网格一般是由圆柱、圆锥、球面等规则曲面以及Bézier、NURBS等自由曲面组合而成[9]，在钢筋混凝土结构中单元表面较为规则，采用高次单元能够较好地逼近结构的曲线和曲面边界[10-11]，提高计算精度。为此，本文提出了两种钢筋线与混凝土单元表面求交方法，能有效得到钢筋结点坐标，适用于任意单元表面，扩大了埋置组合单元模型的适用范围。

1 钢筋线与混凝土单元表面求交方法

在本文提出的两种方法中，第1种是依据有限元中整体坐标与局部坐标的对应关系，利用钢筋线与混凝土单元表面交点对应的局部坐标中必有一项绝对值为1的条件，采用修正的牛顿法，建立求解交点坐标的迭代公式，称为牛顿迭代法。第2种称为分块解析法，可直接采用整体坐标建立混凝土单元表面方程，然后与钢筋直线方程联立求解出交点的整体坐标，再由交点整体坐标求解其局部坐标。依据局部坐标中必有一项绝对值为1的条件，判断交点求解精度，若精度不能满足要求则分块建立曲面方程求解。

1.1 牛顿迭代法

1.1.1 迭代法方程的建立

混凝土单元采用如图1(a)所示的8~20结点等参单元，其中9~20结点为中间结点，可以删除。

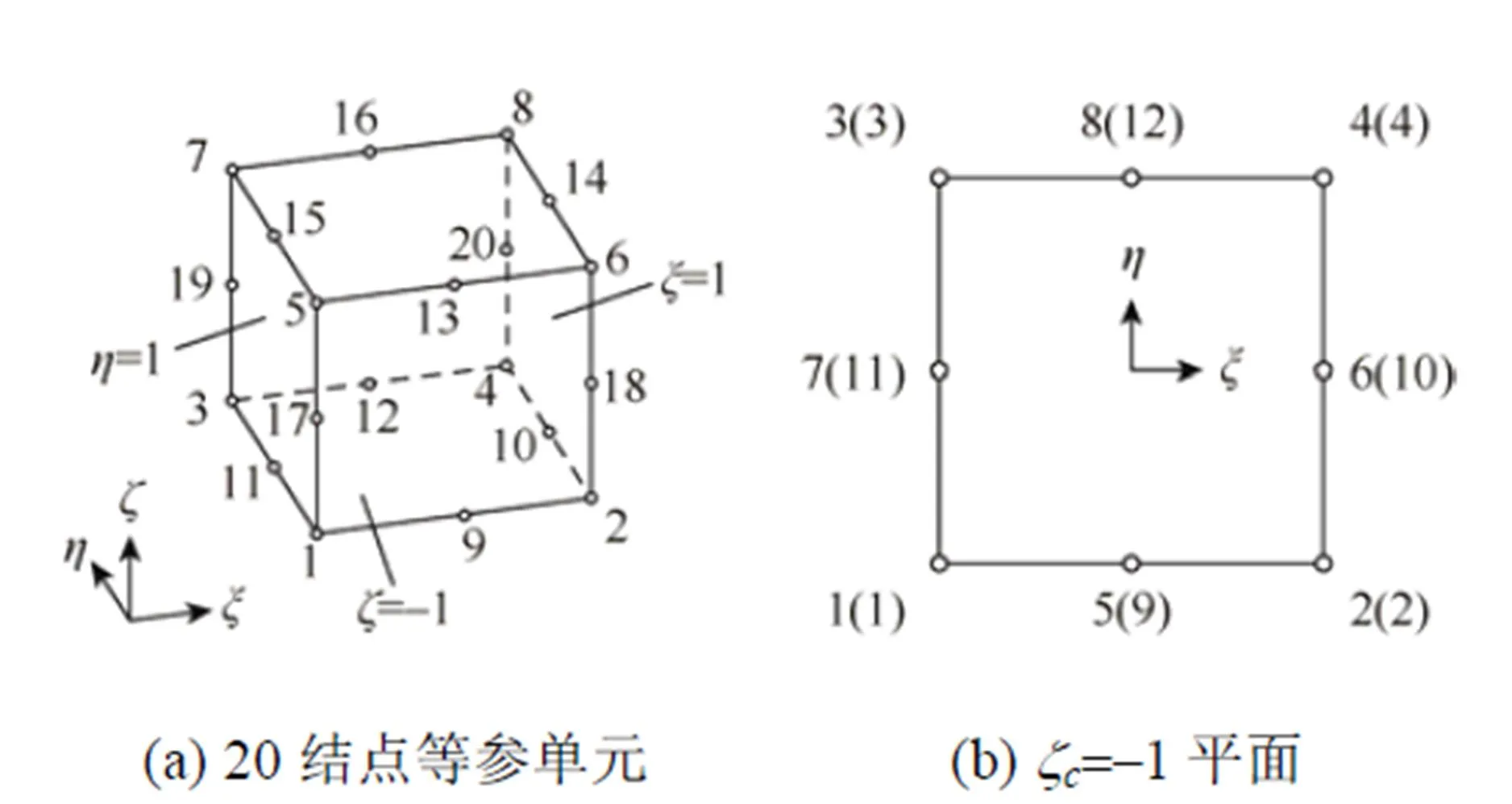
图1 结点编号图

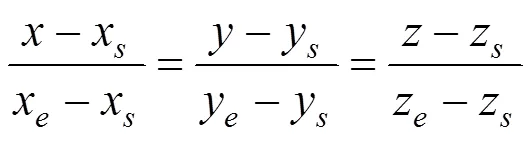
由于钢筋上任意一点均在混凝土单元内，对任意表面形状的混凝土等参单元，必然满足

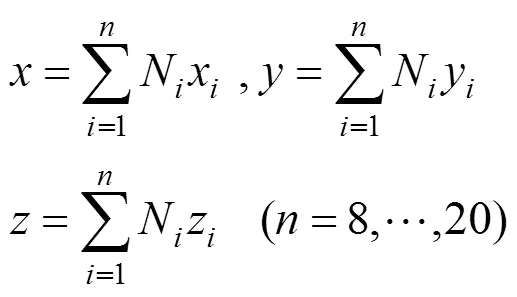
其中，N为有限元形函数；x、y和z为单元结点坐标。

将式(4)代入式(3)，有

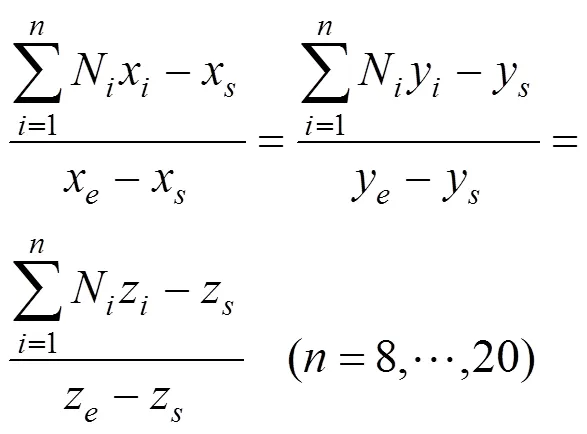
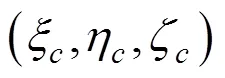
=–1表面对应的形函数N表达式为

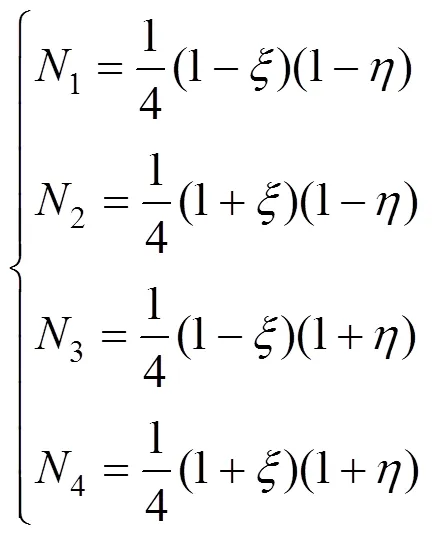
当该面存在中间结点时，中间结点的形函数为

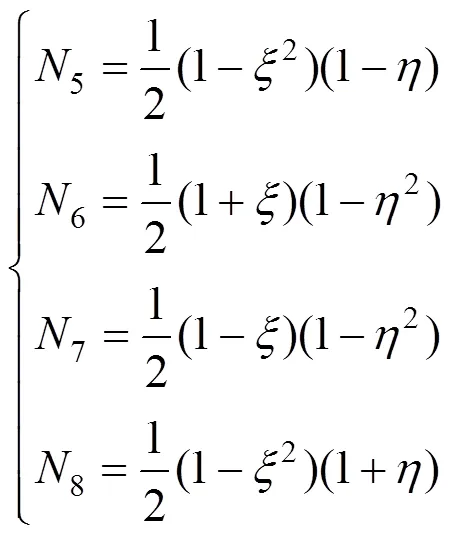
同时对中间结点相邻的两个角结点的形函数进行修改，各减该中间结点形函数的一半。

将式(5)改写成与、有关的方程，即

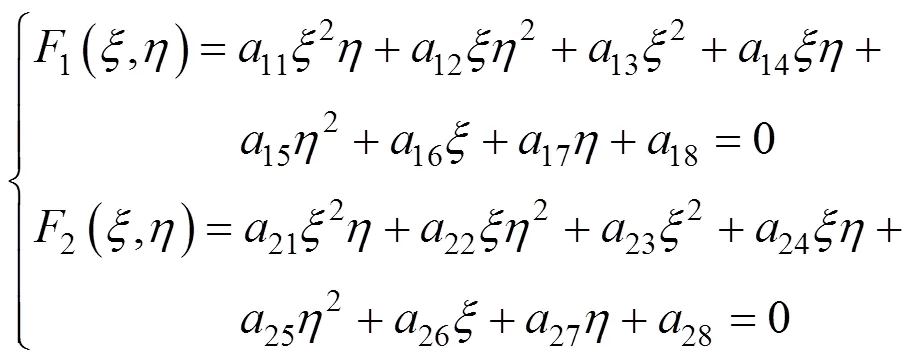
其中，16个待定系数由该平面的结点坐标决定，若没有中间结点，可将式(6)代入，有8个系数不为0，其中4个系数14、16、17、18为

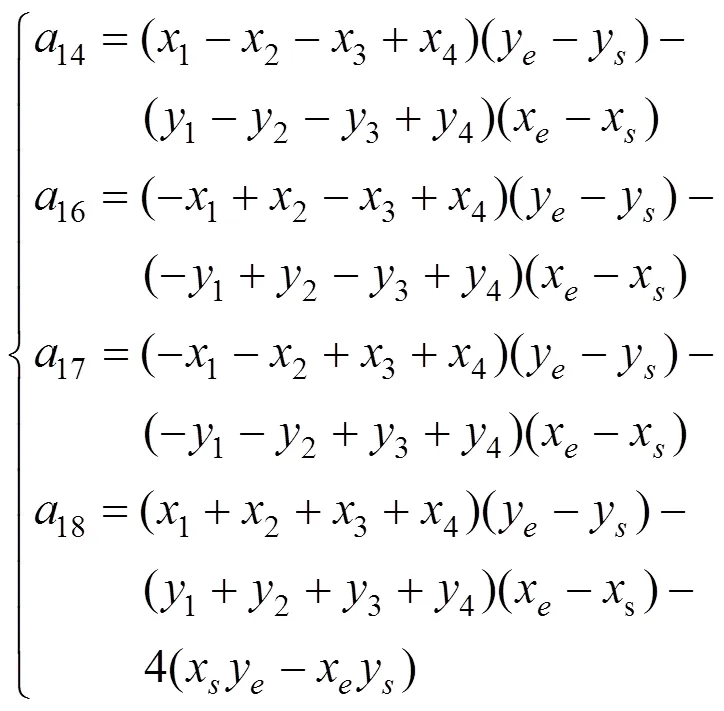
另外4个系数24、26、27、28的表达式可由14、16、17、18表达式中的替换成得到，即

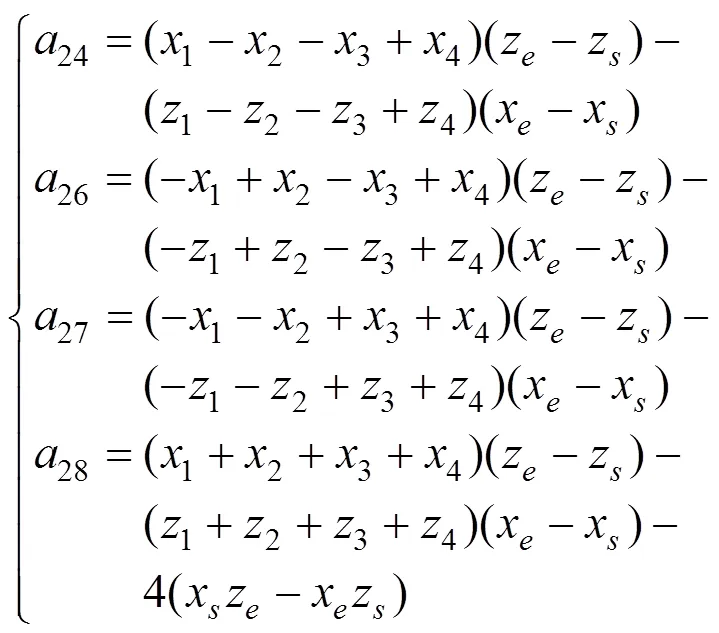
当有中间结点5时，因中间结点5对角结点1和2有影响，式(8)中的系数11、13、21、23不再为0，同时式(9)中的系数17、18、27、28也需修正。式(10)给出11、13、17、18表达式，同样将11、13、17、18表达式中的替换成可得到21、23、27、28表达式。当有其他中间结点时，按照上述思路就可写出相应的表达式，即

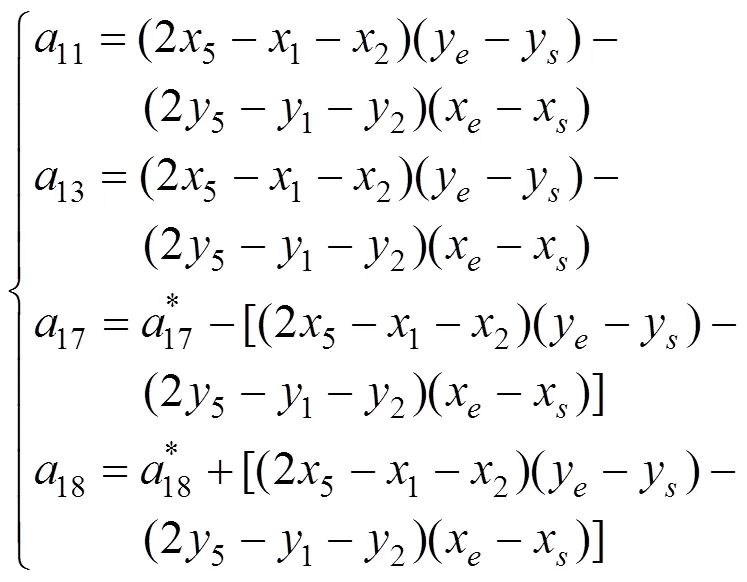
采用Newton法建立迭代式求解非线性方程组式(8)，迭代式为

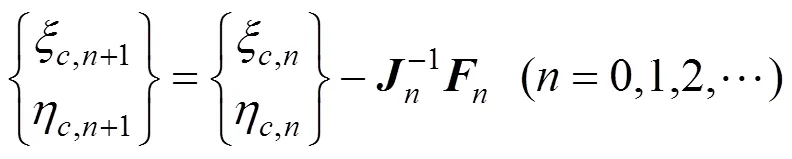
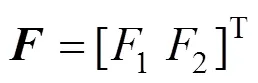
雅可比矩阵表达式及相应系数为

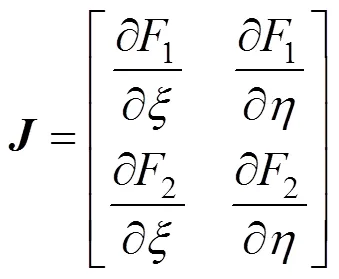
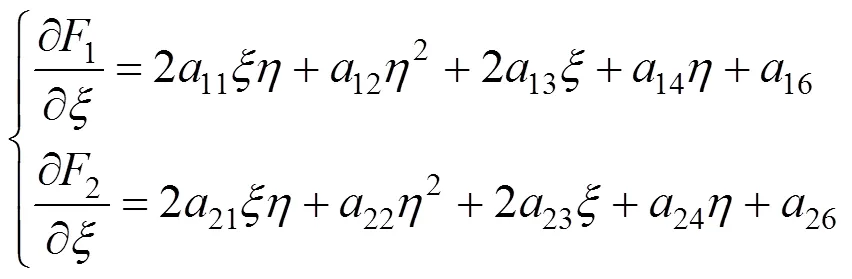
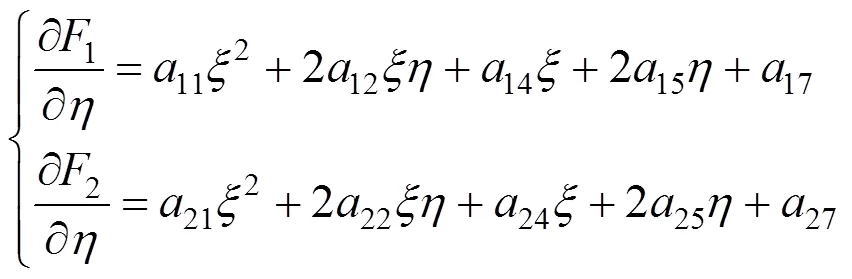
1.1.2 迭代法方程的求解

求解时，首先要判断钢筋线与块体单元表面方程有无交点，可将该面沿对角拆分构成两个平面，若钢筋线与两个平面的夹角都小于一定的限值(可取1°)，则认为钢筋与该表面平行，无交点。另外，还有两种情况需特殊处理：

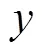
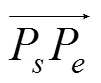
迭代初值的选择直接影响到迭代法的收敛速度。钢筋线与单元表面交点为一个或两个，首先讨论钢筋与表面只有一个交点的情况，图2给出了3种迭代初值的选择方案，分别为：

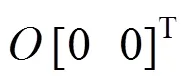
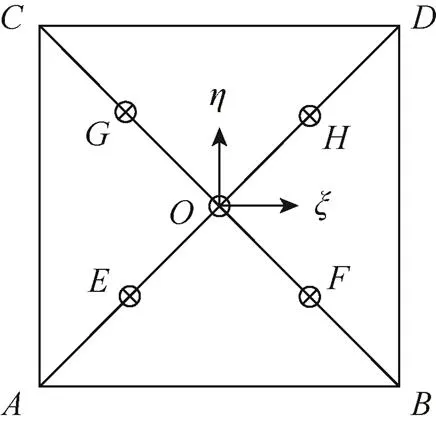
图2 迭代初值点分布图

图3是尺寸为50 mm×200 mm×50 mm的混凝土块体，块体表面规则，单元内表面为曲面。块体内布置了3根钢筋，其起点和终点的整体坐标分别为1号钢筋(25,0,25)®(35,200,25)、2号钢筋(10,0,12)®(40,200,45)和3号钢筋(10,0,10)®(12,200,16)。表1给出上述3种迭代初值方案的计算结果。

图3 钢筋分布图

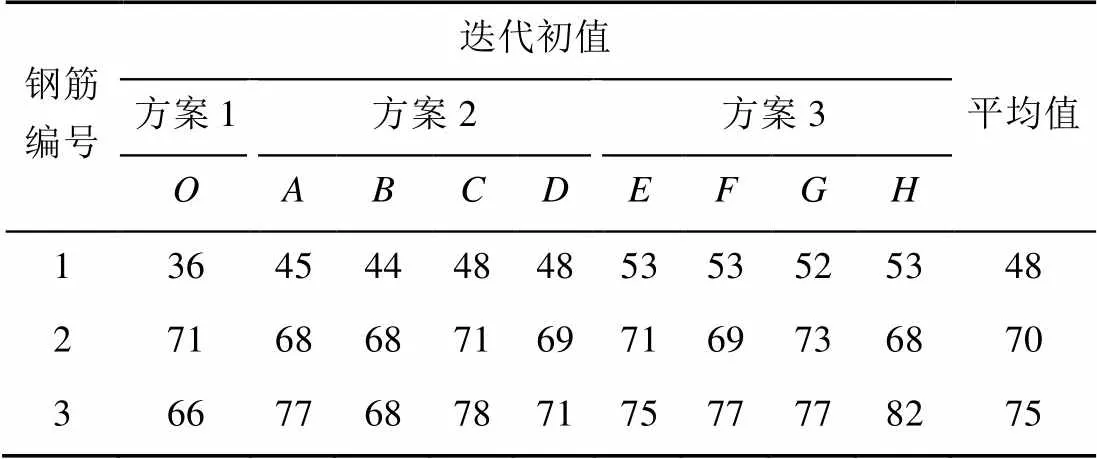
表1 迭代次数

由表1可知，3种方案都能求到真实解，采用方案1时，1、3号钢筋的迭代次数明显少于其余两种方案，2号钢筋的迭代次数与两种方案较为接近。方案1的迭代次数整体偏小，即迭代初值点取等参单元表面的中心点时收敛速度最好。

当表面交点为两个时，给出了2种迭代初值选择方案：

方案1. 以中心点作为迭代初值点，求得第一个交点后，将局部坐标取负号再次进行迭代。

方案2. 分别以4个角点作为迭代初值进行循环，求得两个交点后跳出循环。

下面采用给定结点坐标构造单元表面，考虑两个交点位置的所有可能情况来讨论上述两种方案的可行性。依据等参单元表面中心点将表面划分成4个象限，第1个交点在第3象限，第2个交点分别位于第1、2、3及4象限，如图4所示，即两个交点分别位于3-1、3-2、3-3、3-4象限。表2给出了其计算结果。

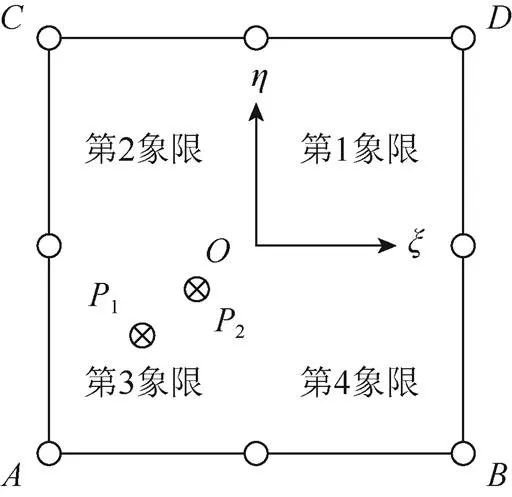
图4 象限划分图

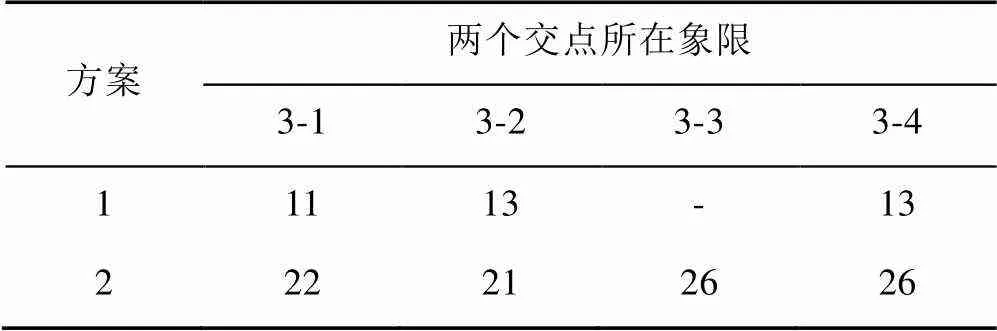
表2 迭代总次数

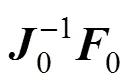
对迭代解还需验证是否为真实的交点，这时先用迭代解局部坐标值,n+1和,n+1是否均在区间[–1,1]内来判断，若成立，再用该交点至钢筋起点P和终点P距离之和是否等于钢筋线总长度来判断，满足则为真实的交点。

1.2 分块解析法

1.2.1 等参单元表面方程建立

先对有中间结点的混凝土单元利用式(4)补全可能缺少的中间结点，使所有混凝土单元为8或20结点等参单元。

建立等参单元表面方程时，先区分是否为平面。在单元表面任取3个结点建立平面方程，若其余结点都满足该平面方程则该表面为平面，该平面方程就是该面的表面方程。

若等参单元表面为曲面，则分8和20结点等参单元两种情况分别建立表面方程。

(1) 8结点等参单元。对于8结点等参单元，其表面的边界线均为直线，当该曲面不经过坐标原点时曲面方程通式为

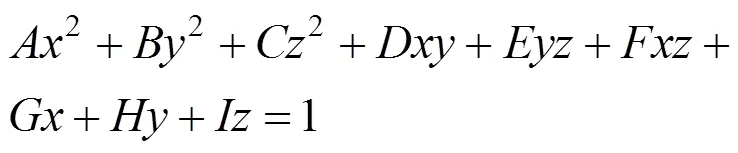
其中，为9个待定系数。

利用已知的4个角点由式(4)插值得到4个中间结点和1个表面中点的结点坐标，组成9个坐标点后代入式(13)，就形成包含9个待定系数的非齐次线性方程组，采用高斯消去法求解就可得这9个待定系数。若该曲面经过原点，可进行平移变换求得交点。

(2) 20结点等参单元。对于20结点等参单元，一般情况下采用与8结点单元相同的方法能求得单元表面方程，但对下列两种情况需特别处理。

①方程通式问题。当式(13)中的某些项不存在时，如母线平行于轴的柱面方程与轴无关，式(13)中待定系数为0，按式(13)求解待定系数时，求解过程中会出现系数矩阵主元为0的情况，这时需将主元为0所在的行与列以及对应行的常数项取为0，同时将该主元取1，以保证方程顺利求解。

②计算精度问题。由于20结点单元棱边存在曲线，当求得的交点局部坐标不能满足计算精度的要求时，可利用中间结点将该面分成4个子块(图5)，分别建立表面方程求解，即分块求交。当计算精度还不满足时，可再次分块求交，如图6所示。

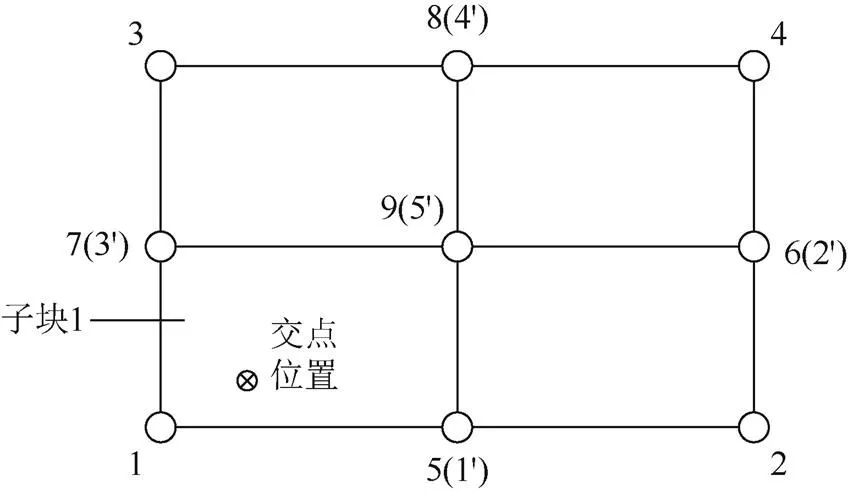
图5 分块结点图

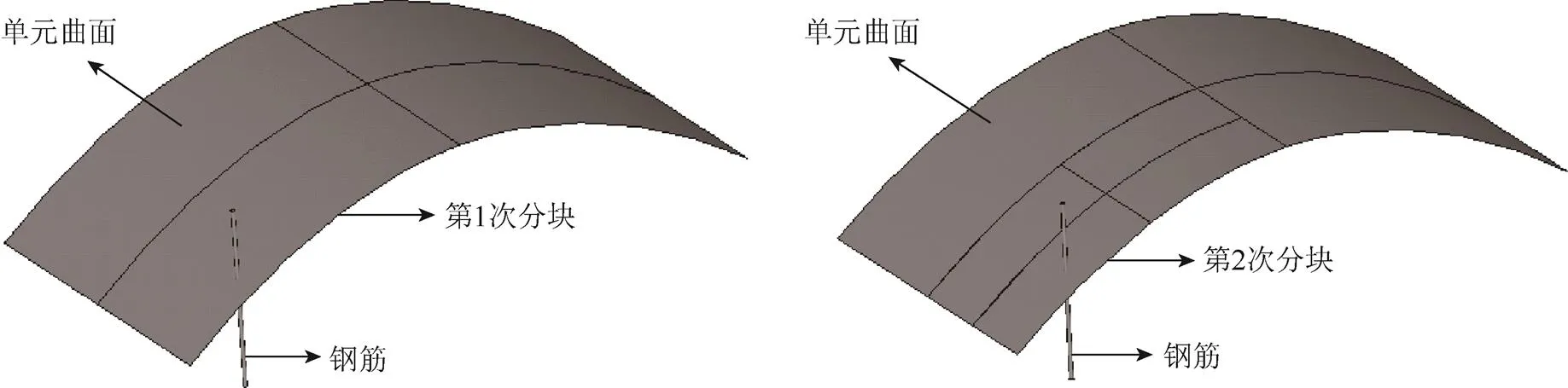
图6 逐次分块示意图

1.2.2 钢筋直线方程与交点真伪判别

钢筋线直线方程可利用其起点坐标(x,y,z)和终点坐标(x,y,z)写成以为变量的参数方程

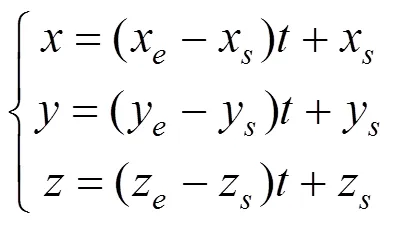
联立式(13)~(14)即可求得交点，交点可能是一个或两个，本文依次采用下述3个步骤确定真实交点：

步骤1.先根据交点与单元边界的位置关系进行判别，交点坐标值必定在单元结点坐标最大值和最小值之间。

步骤2. 再依据交点的局部坐标值进行判别。求交点整体坐标(,,)所对应的局部坐标(,,)可采用下列迭代格式

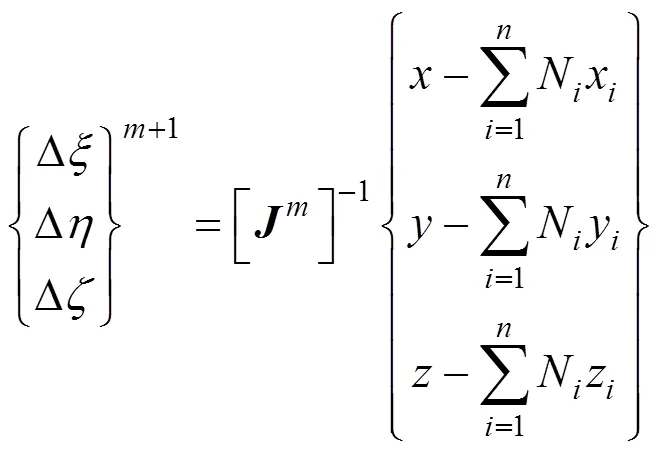
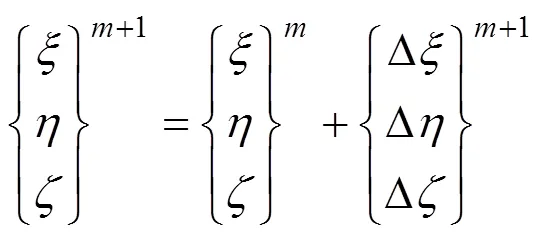
若该交点为实际交点，则局部坐标中必有一项绝对值为1，同时其余两项在[–1,1]区间内。若求得的局部坐标有两项在[–1,1]区间内，另一项绝对值接近1但不满足计算精度要求，则分块求解。

步骤3. 最后用该交点至钢筋起点P和终点P距离之和是否等于钢筋线总长度来判断，若成立则该迭代解为真实的交点。

2 钢筋线与混凝土单元求交过程

钢筋线与混凝土单元表面具体求交过程：

(1) 对所有混凝土单元循环，利用钢筋线起点和终点与单元边界的位置关系确定出钢筋起点P和终点P所在的单元号(该点坐标值必定在所在单元的结点坐标最大值和最小值之间)，记为N和N。

(2) 利用上节所述方法对单元N所有表面求交，找到钢筋线与单元N的交点，并记下交点所在表面S，然后对除N外所有单元循环，找到与S共面的相邻单元N，N即钢筋要进入的下一单元。

(3) 令N=N，对第2步循环，但需注意这时对S面不再求交，直至N=N。

3 算例及处理方法的比较

以一个承台算例来验证本文方法，并对两种方法进行比较。承台截面尺寸为800 mm×800 mm，高700 mm，承台内布置直径12 mm、间距200 mm的分布钢筋。桩沿交界位置向下截取长800 mm的一段，桩身直径为400 mm。采用空间埋置组合式单元模型，剖分混凝土单元时不必考虑钢筋位置，剖分后共有2 176个单元，如图7所示。由于模型中承台网格剖分时受限于桩体网格，沿桩竖直方向的承台网格与桩体网格保持一致，此时会出现钢筋穿过混凝土单元曲面表面的情况。

通过运算发现，两种处理方法得到的结果相同，但由于牛顿迭代法需分别取表面4个角点作为迭代初值，当仅有一个交点时多迭代了3次；相比而言，分块解析法计算简便。由于分布钢筋较多，本文只取靠近桩体两个方向上有代表性的4根分布钢筋，并将模型倒置，最终结果如图8所示。

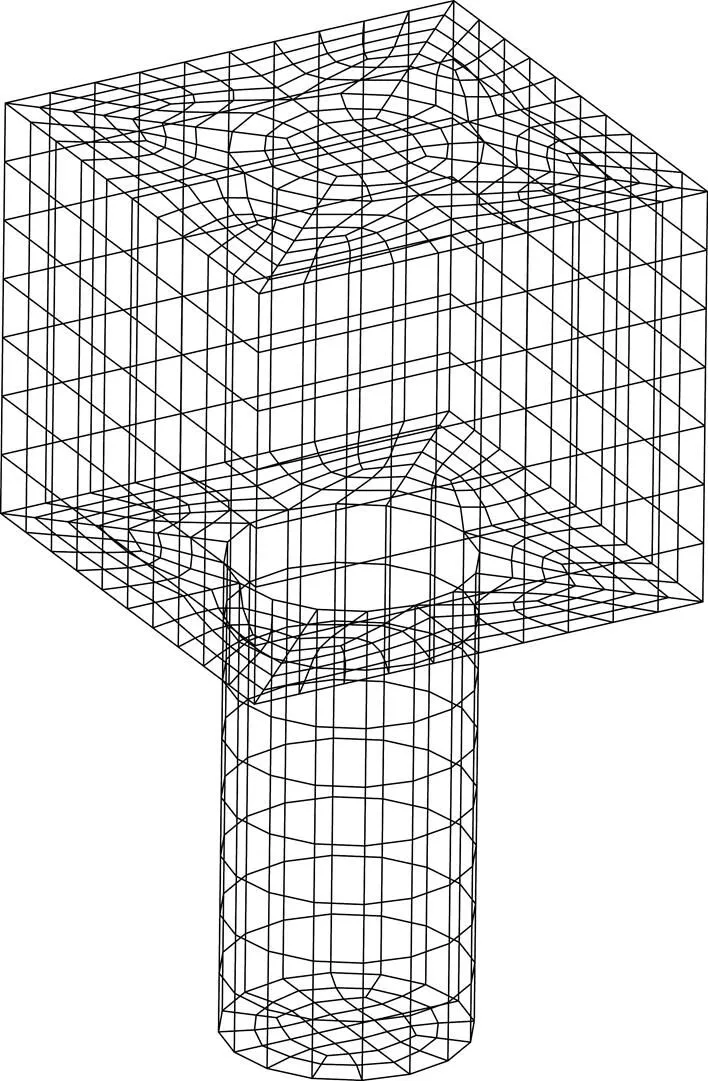
图7 结构有限元网格模型

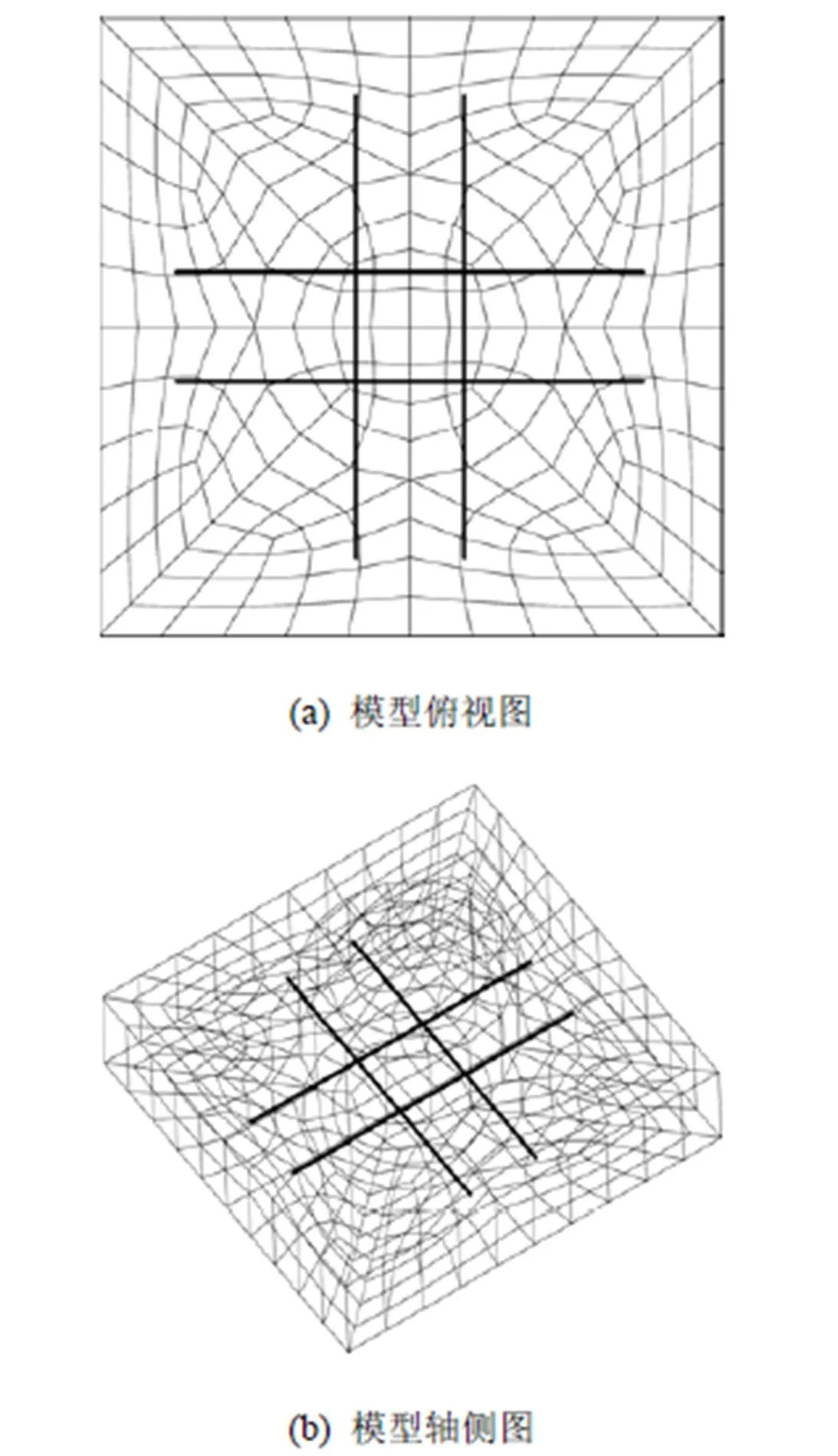
图8 钢筋布置图

4 结束语

(1) 对表面为任意形状的单元，提出了两种钢筋线与混凝土单元表面求交方法，并给出其计算过程。利用这两种方法能有效得到直钢筋穿过混凝土单元表面的钢筋结点坐标信息，增强了空间埋置组合单元模型的适用性。

(2) 两种求交方法均能得到正确解。牛顿迭代法需分别取表面4个角点作为迭代初值进行迭代，当仅有一个交点时多迭代了3次；分块解析法利用方程直接求出表面交点，计算简便。从适用性而言，分块解析法要优于牛顿迭代法。

[1] 江见鲸, 陆新征. 混凝土结构有限元分析[M]. 2版. 北京: 清华大学出版社, 2013: 129-133.

[2] NGO D, SCORDELIS A C. Finite element analysis of reinforced concrete beams [J]. Journal of American Concrete Institute, 1967, 64(3): 152-163.

[3] GOODMAN R E, TALYOR R L, BREKKE T L. Closure on a model for the mechanics of jointed rock [J]. Journal of the Soil Mechanics and Foundations Division, 1970, 94(3): 637-660.

[4] SUIDAN M, SCHNOBRICH W C. Finite element analysis of reinforced concrete [J]. Journal of the Structural Division, 1973, 99: 2109-2122.

[5] CHANG T Y, TANIGUCHI H, CHEN W F. Nonlinear finite element analysis of reinforced concrete panels [J]. Journal of Structural Engineering, 1987, 113(1): 122-140.

[6] ZIENKIEWICZ O C, OWEN D R J, PHILLIPS D V, et al. Finite element methods in the analysis of reactor vessels [J]. Nuclear Engineering & Design, 1972, 20(2): 507-541.

[7] 汪基伟, 张雄文, 林新志. 考虑粘结滑移的平面组合式单元模型研究与应用[J]. 工程力学, 2008, 25(1): 97-102.

[8] 巫昌海, 汪基伟. 混凝土三维钢筋埋置组合式有限单元模型及其网格自动生成[J]. 计算机辅助设计与图形学学报, 2000, 12(10): 761-764.

[9] 关振群, 宋超, 顾元宪, 等. 有限元网格生成方法研究的新进展[J]. 计算机辅助设计与图形学学报, 2003, 15(1): 1-14.

[10] 古成中, 吴新跃. 有限元网格划分及发展趋势[J]. 计算机科学与探索, 2008, 2(3): 248-259.

[11] 王明强, 朱永梅, 刘文欣. 有限元网格划分方法应用研究[J]. 机械设计与制造, 2004(1): 22-24.

Surface Intersection Algorithm Based on Spatial Embedded Finite Element Model

WANG Jiwei1, FU Yu1, WANG Yajiang2

(1. College of Civil and Transportation Engineering, Hohai University, Nanjing Jiangsu 210098, China; 2. Quanzhou Audit Bureau, Quanzhou Fujian 362000, China)

In the spatial embedded finite element model, the bar element can be embedded at any position in the concrete element. The element model is convenient because the mesh of the concrete element is not limited by the reinforcement. In the application of the element model, it is necessary to obtain the coordinates where the both ends of the steel element lie at the surface of the concrete element. Therefore, it is the premise of application of the model to solve the intersection of the reinforcement line and the concrete element surface. The existing method is only suit for the concrete element with plane surface. In this paper, the Newton iterative method and the divided block analytic method are proposed which can solve the intersection of the reinforcement line and the surface of concrete element with any shape. The method in the paper can enhance the applicability of the spatial embedded finite element model. The correctness of the two methods is verified by an example. In terms of applicability, the divided block analytic method is superior to the Newton iterative method.

reinforced concrete finite element method; element model; pre-processing of finite element method; curved surface

TP 391；TU 375

10.11996/JG.j.2095-302X.2018020221

A

2095-302X(2018)02-0221-07

2017-08-04；

2017-09-14

国家重点研发计划项目(2016YFC0402002)

汪基伟(1962–)，男，浙江安吉人，教授，博士，博士生导师。主要研究方向为钢筋混凝土。E-mail：wjw2903918@126.com