基于各向异性全变分的迭代滤波算法

芦碧波，王乐蓉，郑艳梅，王永茂，李晓莹，秦钰翔



基于各向异性全变分的迭代滤波算法

芦碧波1,2，王乐蓉1，郑艳梅1，王永茂1，李晓莹1，秦钰翔1

(1. 河南理工大学计算机科学与技术学院，河南 焦作 454000；2. 广东省数据科学工程技术研究中心，广东 广州 510631)

空间邻近度和像素值相似度的双边滤波(BF)器在滤波时，由于其值域滤波核系数的计算易受到噪声的干扰，在噪声水平较大时，直接使用噪声图像来指导核函数权值计算的方案不可行。为此，提出一种结合各向异性全变分和BF的图像去噪算法，将各向异性全变分算法与BF算法相结合，首先利用各向异性全变分算法对噪声图像进行处理，得到一幅边缘结构信息较为丰富的结果图像，接着将该结果图像作为BF算法的引导图像来指导值域滤波核系数的计算，为保证算法的稳定性，对上述过程进行迭代处理。此外，为提高各向异性全变分算法的计算效率，引入了Split Bregman迭代算法进行加速处理。实验表明，该算法能在较好去噪的同时，保留较多的边缘结构信息。

图像去噪；双边滤波；各向异性全变分算法；Split Bregman迭代方法；结构保持能力

图像中噪声的存在导致了图像质量的下降，图像降质不仅给用户带来了不便，也阻碍了图像后续处理任务的进行，因此，图像去噪往往是图像处理任务中的第一步。滤波是图像去噪的重要手段之一，根据降噪处理空间的不同，滤波主要可以分为频率域滤波和空间域滤波两大类。常见的频率域滤波方法有小波变换、傅里叶变换等，其基本原理是将图像从空间域转换到频率域中进行处理，之后再通过反变换到空间域；常见的空间域滤波方法有均值滤波、中值滤波和高斯滤波等，其基本原理是借助模板对图像中的每个点与其相邻的像素点作邻域运算。对于实际生活中常见的加性高斯噪声，高斯滤波有着较好的处理效果。但由于该方法只考虑了空间上的邻近关系，导致其在平滑图像的同时也退化了边缘[1]。为了克服这一缺点，1998年TOMASI和MANDUCHI[2]提出了双边滤波(bilateral filtering，BF)方法。

BF算法是基于高斯滤波的一种改进算法，其不仅考虑了像素空间上的邻近关系，也考虑了像素值间的相似性。通过对两者的非线性组合，能够在滤除噪声的同时保留更多的边缘信息。因为BF算法简单且较容易实现，被广泛应用于图像去雾[3]、图像增强[4]等领域中。然而，由于BF算法是使用噪声图像来指导加权系数的计算，在噪声水平较小的情况下，该方案可行，但当噪声水平较高时，噪声图像的结构信息被噪声破坏，严重影响了值域核加权系数的准确计算，导致其去噪效果变差。

文献[5]指出，若直接使用清晰图像来引导值域核加权系数的计算会极大改善去噪效果。虽然在去噪问题中使用清晰图像引导BF进行去噪是一种无法实现的悖论，但寻找一幅优于噪声图像的引导图像是可行的。基于此，出现了很多BF的改进算法，例如2005年XU和PATTANAIK[5]提出了用高斯滤波计算后的结果图像来引导BF去噪的模型；2009年ZHOU等[6]提出了二次迭代双边滤波(doubly bilateral filtering，DBF)，即用第一次双边滤波的结果来指导第二次双边滤波；2015年CHAUDHURY和RITHWIK[7]提出了加权双边滤波(weigthted bilateral filtering，WBF)，该方法是使用BF和鲁棒的BF进行加权，其中鲁棒的BF是先使用均值滤波对噪声图像进行预处理，而后用预处理后的结果图像来引导BF去噪。但由于以上方法均存在滤波结果图像结构丢失的情况，其效果仍不能令人满意。

考虑到各向异性全变分算法[8-9]能够较好的保持图像边缘结构信息，基于此，本文充分结合各向异性全变分算法和BF算法的优势，提出了各向异性全变分引导BF去噪的方法，并利用了Split Bregman迭代算法[10-11]对该模型进行快速求解。实验表明，本文算法在较好去噪的同时保留了更多的纹理结构信息，明显改善了图像质量。

1 基于各向异性全变分的双边滤波算法

1.1 双边滤波

图像去噪的目标是从噪声图像中获得最近于原始图像的估计值，本文使用零均值加性高斯噪声作为噪声模型，即

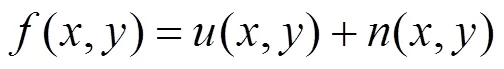
其中，为无噪声图像；是均值为0、标准差为的高斯白噪声；为噪声图像；Ω为图像的定义域，像素点(,)ÎΩ。

为了尽可能地滤除噪声图像中的噪声，还原无噪声图像，BF利用局部加权平均的思想来计算复原图像的像素值，其模型公式为

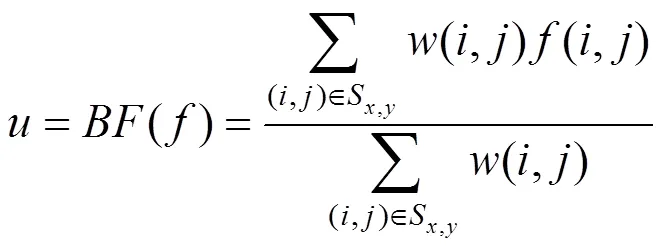
其中，S,y表示中心点为(,)的(21)(2+1)大小的邻域，对该邻域内的每一像素点(,)，其加权系数(,)均由两部分因子的乘积组成，即

其中空域核函数和值域核函数的计算公式分别为

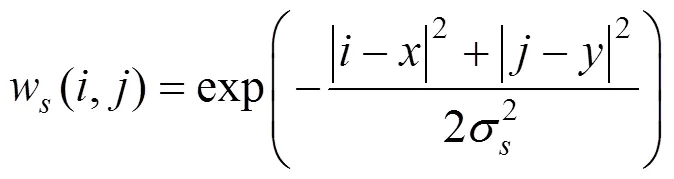
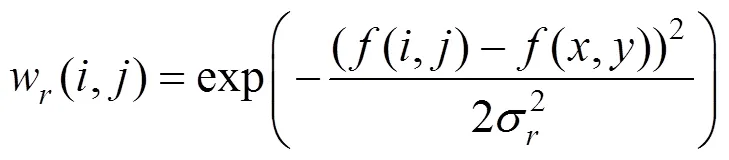
从式(3)可看出，BF器的加权系数由两个高斯核函数组成，一个是空域核函数，由图像的几何空间距离决定，距离越小，权值越大；另一个是值域核函数，由图像的像素差值决定，像素值越接近，权值越大；通过将这两个核函数进行乘积，可以实现图像的自适应滤波。在图像变化平缓的区域，值域滤波核函数接近1，此时空域滤波起主要作用，BF器退化为传统的高斯滤波器，对图像进行平滑操作。而在图像边缘部分，由于像素间的差异较大，此时值域滤波起到了保护边缘信息不被模糊的作用。

1.2 引导图像的分析与选择

从式(5)可看出，BF器使用的是噪声图像来引导值域核函数的计算，的结构信息与吻合程度越高，值域核函数的计算就越准确。但是，当噪声较多时，引导图像的结构信息被湮没，无法为值域核函数的计算提供有效的引导信息，影响加权系数的准确性从而进一步影响了BF的去噪效果。为此，需要寻找更为合理的引导图像构造加权函数。在文献[7]中，研究人员使用均值函数处理噪声图像，并将其结果用来构造加权函数，取得了一定的效果。均值函数虽然可以减少噪声的影响，但也不可避免模糊边界等重要特征。

为了利用噪声图像构造清晰的引导图像、改善去噪效果，本文选用了基于L1范数的各向异性全变分算法(anisotropic TV，ATV)来构造引导图像，即

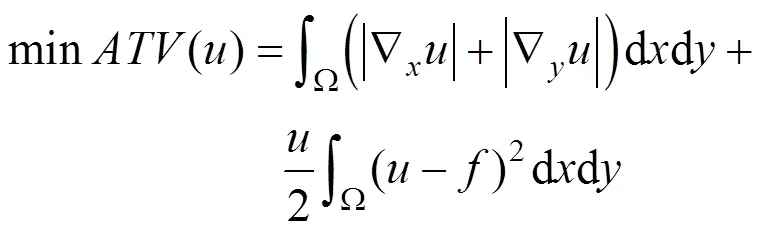
其中，第一项是正则项，要求输出的结果图像具有良好的结构信息且光滑；第二项是拟合项，要求输入和输出图像间具有一定的相似性，能够保留原图像的特征；参数为规整参数，其依赖于噪声水平。

由模型定义可知，该模型利用图像内在的正则性进行去噪，易于从噪声图像中得到包含清晰图像结构的解，输出一个包含较为丰富的边缘等重要结构信息结果图像。

1.3 各向异性全变分引导双边滤波去噪模型

基于各向异性全变分算法可以较好保持图像结构信息的优势，本文考虑将各向异性全变分算法与BF相结合，利用各向异性全变分算法得到的结果图像作为BF的引导图像。同时，为了避免各向异性全变分算法在光滑过渡区域恢复过程中产生的块状效果即阶梯效应，设计了一种相互迭代的策略，使用BF的加权平均机制对阶梯效应进行抑制，以改善最终的滤波效果。具体迭代式为

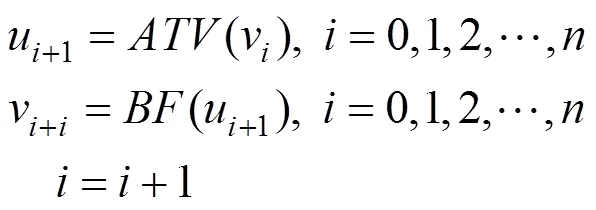
初始条件u0=v0=f，其具体算法流程为：首先输入噪声图像u0=v0=f，接着利用各向异性模型对噪声图像进行计算得到结果图像ui+1；然后将ui+1作为BF的引导图像输入进行BF得到结果图像vi+1，如此循环迭代，直到图像达到良好地去噪效果为止(图1)。

2 各向异性全变分引导双边滤波去噪的快速算法

2.1 各向异性全变分算法的Split Bregman算法

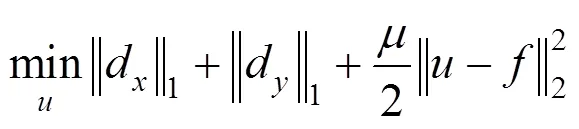
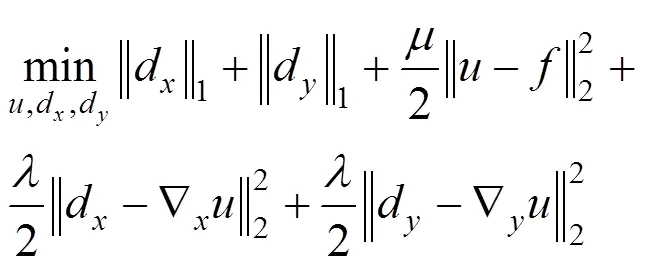
通过Split Bregman算法可以得到迭代式为

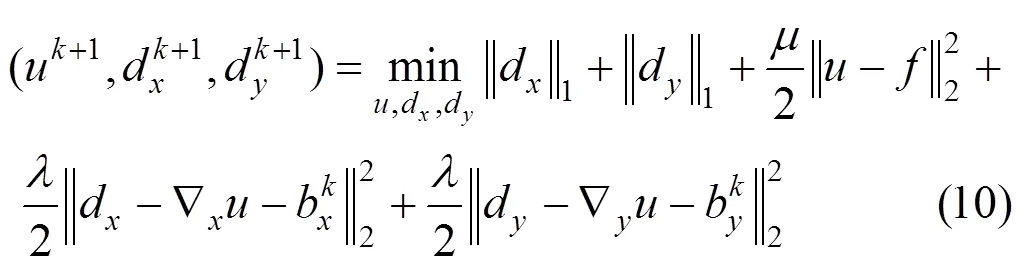
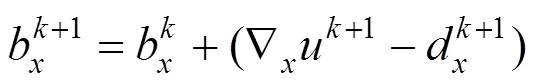
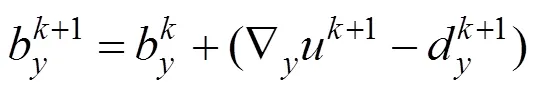
注意到该能量函数的第一项是保证光滑，为了得到，令式(10)关于的导数等于零可得到

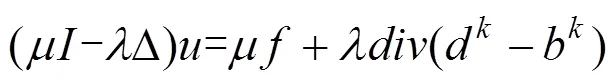
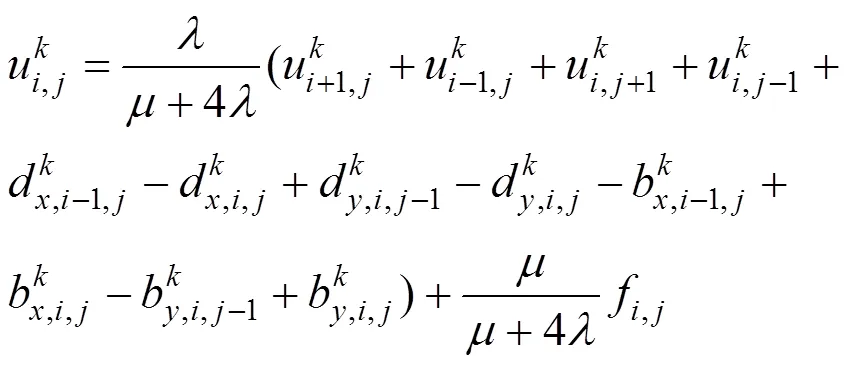
最后利用收缩式(10)计算d和d的迭代式

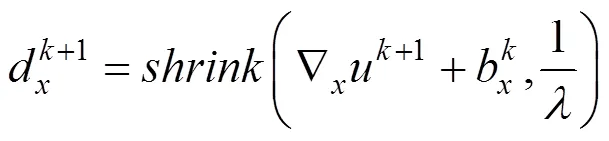
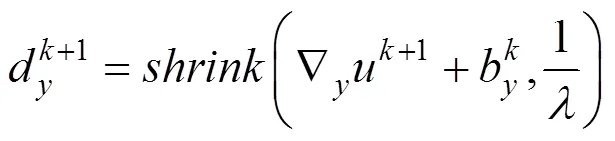
2.2 各向异性全变分引导双边滤波去噪的Split Bregman算法

综上所述，本文算法的计算步骤如下：

3 实验结果

为验证本文算法的有效性，利用Matlab R2015b分别对Cameraman、Lena、Lake和Pepper图像进行了仿真实验，并与BF算法、DBF算法和WBF算法进行了对比。

图2给出了Cameraman图像(256´256)在噪声水平=10的去噪结果，图3给出了Lake图像(512´512)在噪声水平=20的去噪结果。为进一步从主观上体现各个算法的去噪效果，给出了对比算法的局部放大图：其中(a)为原始图像，(b)为添加噪声后的图像，为添加高斯白噪声的方差；(c)为BF结果；(d)为DBF结果；(e)为WBF结果；(f)为本文算法结果；图(g)~(k)分别为图(b)~(f)的局部放大图。

图2 Cameraman图像去噪结果对比

图3 Lake图像去噪结果对比

从图2对Cameraman图像的测试表明，在噪声较小的情况下，各个算法的去噪效果区别不明显，因为少量的噪声没有对图像的结构造成较大的影响，仍保留了原图像较多的结构信息，此时用噪声图像来引导BF算法，可以得到较好的结果。但从局部放大图中看出，本文算法比其他3种算法有着较强的边缘结构保持能力，且较完整地保留了原图像中建筑物的结构信息。

从图3对Lake图像的测试表明，当噪声增大时，BF算法的抑噪能力变差，残留了较多噪声；DBF和WBF算法则出现了不同程度的模糊现象，丢失了部分图像细节信息；而本文算法的优势得以体现，从对白云的放大图来看，由本文算法计算得到的结果图像在视觉上表现的更加自然。

为进一步验证各个算法的纹理保护能力，图4和5分别给出了Lena和Pepper图像在不同噪声水平情况下各算法的对比。从差值图像中可以看出各算法的结构保持能力，若差值图像中出现有用的结构信息越少，证明该算法的纹理保护能力越强。

从图4和5的去噪结果对比得到，在噪声较多情况下，使用BF算法进行去噪的效果较差，因为大量的噪声湮没了原图像中的有用信息，此时的噪声图像不能够为BF算法提供有效的引导信息，丢失了较多的图像细节信息；DBF算法是将BF算法迭代了两次，导致结果图像的部分区域出现了过平滑现象；WBF算法虽较前两者有效地提高了去噪效果，但由于该算法使用了均值滤波进行预处理，其结果图像不可避免地出现了模糊现象；相比之下，本文算法的去噪效果较为明显，能够在噪声较多的情况下保持其良好的去噪性能。此外，从残差图像中看出，BF、DBF和WBF算法的残差图中残留了较多的边缘结构信息，而本文算法的残差图出现的有用的结构信息较少，得益于使用了各向异性全变分算法来进行建模的结果。

为客观评价各个算法的去噪性能，本文选取了峰值信噪比(peak signal to noise ratio，PSNR)来进行图像质量的评价。

图4 Lena图像去噪结果对比

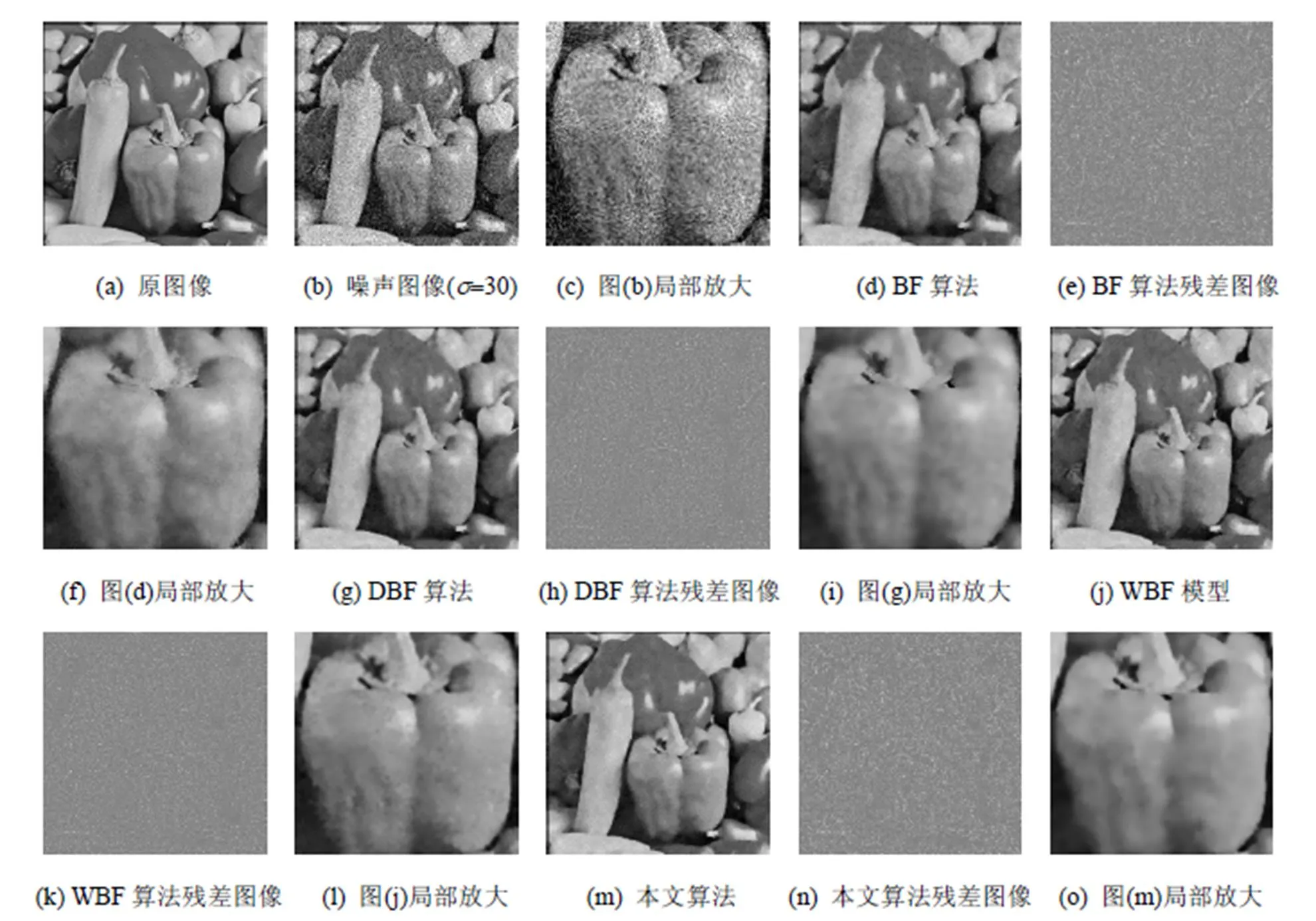
图5 Pepper图像去噪结果对比

通常，PSNR越高，图像的去噪效果越好。其计算式为

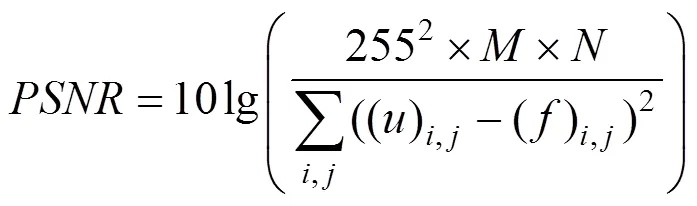
其中，、分别为图像的行列数。

表1给出了4种模型的PSNR值。由实验数据显示，本文算法的PSNR值较BF算法、DBF和WBF有了明显的提高，验证了本文算法其较好的去噪性能。

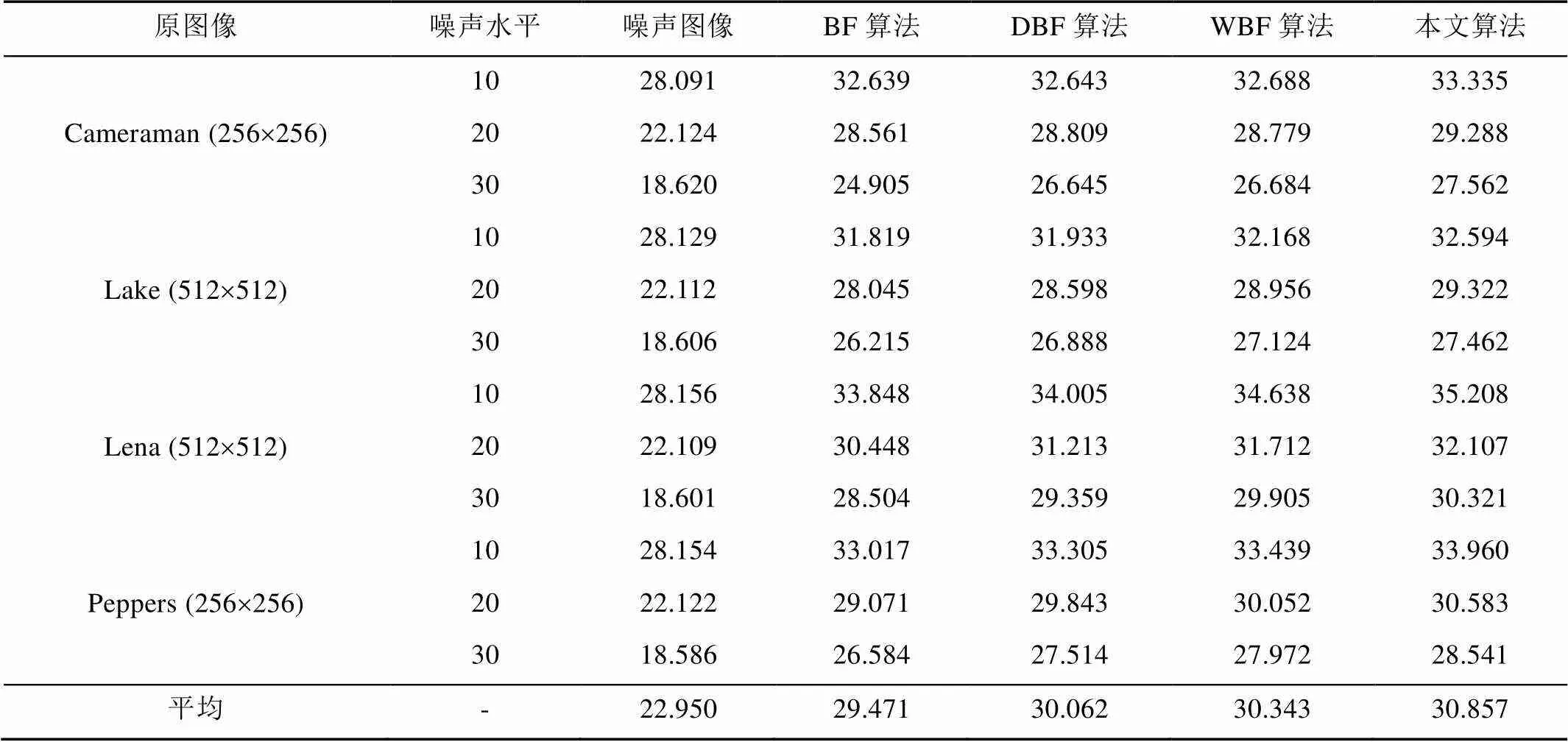
表1 峰值信噪比对比(dB)

4 结 论

本文结合各向异性全变分算法与BF算法，提出了各向异性全变分引导BF去噪的迭代方法，并引入Split Bregman迭代算法对该模型进行加速求解。通过数值实验证明，本文算法可以在较好去除噪声的同时较好的保持边缘结构信息，有效地解决了BF算法在噪声水平变大时，其去噪性能变差这一缺点。

[1] 姒绍辉, 胡伏原, 顾亚军, 等. 一种基于不规则区域的高斯滤波去噪算法[J]. 计算机科学, 2014, 41(11): 313-316.

[2] TOMASI C, MANDUCHI R. Bilateral filtering for gray and color images [M]. New York: IEEE Press, 1998: 839.

[3] 胡韦伟, 汪荣贵, 方帅, 等. 基于双边滤波的Retinex图像增强算法[J]. 图学学报, 2010, 31(2): 110-115.

[4] 王一帆, 尹传历, 黄义明, 等. 基于双边滤波的图像去雾[J]. 中国图象图形学报, 2014, 19(3): 386-392.

[5] XU R, PATTANAIK S N. A novel monte carlo noise reduction operator [J]. Computer Graphics & Applications IEEE, 2005, 25(2): 31-35.

[6] ZHOU Z F, CAO J Z, WANG H, et al. Image denoising algorithm via doubly bilateral filtering [C]//International Conference on Information Engineering and Computer Science. New York: IEEE Press, 2009: 1-4.

[7] CHAUDHURY K N, RITHWIK K. Image denoising using optimally weighted bilateral filters: a sure and fast approach [C]//IEEE International Conference on Image Processing (ICIP). New York: IEEE Press, 2015: 108-112.

[8] GEMECHU D, YUAN H, MA J. Random noise attenuation using an improved anisotropic total variation regularization [J]. Journal of Applied Geophysics, 2017, 144: 173-187.

[9] GRASMAIR M, LENZEN F. Anisotropic total variation filtering [J]. Applied Mathematics & Optimization, 2010, 62(3): 323-339.

[10] GOLDSTEIN T, OSHER S. The split bregman method for L1-regularized problems [J]. Siam Journal on Imaging Sciences, 2009, 2(2): 323-343.

[11] MA W, OSHER S. A TV Bregman iterative model of retinex theory [J]. Inverse Problems & Imaging, 2017, 6(4): 697-708.

[12] VOGEL C R, OMAN M E. Iterative methods for total variation denoising [J]. Siam Journal on Scientific Computing, 1997, 17(1): 227-238.

An Iterative Image Filter Based on Anisotropic Total Variation

LU Bibo1,2, WANG Lerong1, ZHENG Yanmei1, WANG Yongmao1, LI Xiaoying1, QIN Yuxiang1

(1. College of Computer Science and Technology, Henan Polytechnic University, Jiaozuo Henan 454000, China; 2. Guangdong Engineering Research Center for Data Science, Guangzhou Guangdong 510631, China)

Spatial proximity and similarity of the pixel values of bilateral filter in the filter based on the calculation of the range of filter kernel coefficient is susceptible to noise interference. When the noise level is high, the direct use of noise image to guide the kernel weight computation program is not feasible. Therefore, in this paper, the anisotropic total variation and bilateral filtering are combined. Firstly, the image is processed by the anisotropic total variation model, and the result image with rich edge structure information is obtained. Then the calculation results of image as a guide bilateral filtering image to guide the range of filter kernel coefficient. In order to ensure the stability of the algorithm, the above process is iterated. In addition, in order to improve the computational efficiency of the anisotropic total variation model, the Split Bregman iterative algorithm is introduced to accelerate the computation. The experimental results show that the proposed algorithm can preserve more edge information while denoising.

image denoising; bilateral filter; anisotropic total variation; Split Bregman iterative method; structure preserve capability

TP 391

10.11996/JG.j.2095-302X.2018020186

A

2095-302X(2018)02-0186-07

2017-06-19；

2017-08-13

国家自然科学基金项目(U1404103)；河南省教育厅科学技术研究重点项目(14A520029，16A520053)；河南理工大学创新型科研团队项目(T2014-3)；河南理工大学博士基金项目(B2016-40)

芦碧波(1978–)，男，河南焦作人，副教授，博士。主要研究方向为数字图像处理。E-mail：lubibojz@gmail.com