改进的流体模拟固体边界处理算法

朱晓临，殷竞存，汪欢欢



改进的流体模拟固体边界处理算法

朱晓临，殷竞存，汪欢欢

(合肥工业大学数学学院，安徽 合肥 230009)

流体模拟是计算机图形学的一个重要研究分支，流体的固体边界处理一直是流体模拟的研究重点，光滑粒子流体动力学(SPH)方法中的镜像粒子法是处理固体边界的一个重要方法。镜像粒子法通过靠近边界的流体粒子在边界外动态生成对应的镜像粒子来处理固体边界问题，但随着边界复杂程度的提高，传统的镜像粒子法生成镜像粒子的复杂度也随之提高，模拟效率随之降低。为此，文章对镜像粒子法进行改进，提出一种新的镜像粒子场量求值方法，有效地降低了复杂边界情况下生成镜像粒子的复杂度，且使靠近边界的流体粒子场量更加均匀。仿真实验结果表明，随着流体模拟粒子数的增加以及边界复杂程度的提高，该方法比传统镜像粒子法效率高的优势也更加明显。

光滑粒子流体动力学方法；流体模拟；固体边界处理；镜像粒子法；复杂场景

基于物理的流体模拟方法一直是计算机动画领域的一个研究热点，在游戏、广告和影视特效中得到了广泛应用。流体的固体边界处理更是计算机动画中流体模拟技术的重要研究内容。

光滑粒子流体动力学(smoothed particle hydrodynaimics，SPH)方法的流体模拟中存在3类流固耦合方法：惩罚力方法、镜像粒子法和静态粒子法。

惩罚力方法是通过构造一种基于距离和速度的惩罚力函数，对靠近边界的流体粒子施加反作用力以防止流体穿透固体边界。但是，当惩罚力较大时，会导致边界处流体粒子的压强出现明显变化，惩罚力较小时，流体粒子就会非物理性穿透边界。此外，由于边界截断，流固交界面上流体粒子数量会相对不足，流体粒子就会附着在固体边界上。镜像粒子法，即靠近边界的流体粒子在边界外动态生成对应的镜像粒子，一定程度上能够提高流体边界粒子精度以及流固交界面处流体的压强分布均匀，但存在着对于复杂和可变形固体边界难以生成镜像粒子的问题。静态粒子法在边界外分布几层固定的边界粒子，并将其看作位置固定的特殊流体粒子参与流体的物理计算过程。该方法实施简单，但是在运动剧烈时流体粒子容易穿透。

MONAGHAN[1]使用L-J形式的基于粒子距离计算粒子间的相互作用力，但是忽略了边界处流体粒子运动方向与边界平行，易造成流体紊动现象。MONAGHAN和PRICE[2]提出新的构造函数，解决了上述问题。MÜLLER等[3]基于惩罚力方法实现了微可压缩SPH流体与可变形固体之间的交互模拟。使用较大的惩罚力能够保证流体不会穿透固体边界，但同时必须使用较小的时间步以保证模拟的稳定性。BECKER等[4]提出了直接力方法，通过预测-校正技术，对粒子速度和位置进行分布计算。上述方法都存在一个问题，由于流固交界面上流体粒子数量不足而造成流体粒子附着在固体边界上。HARADA等[5]针对这类问题提出了一种边界权重函数，通过计算流体粒子到边界的垂直距离，可以在流体密度计算中加入固体边界的贡献以弥补边界粒子的不足。该方法解决了流体粒子的附着问题，但只适合规则固体边界的情况，且会导致固体边界处流体密度分布不均匀。

HU和ADAMS[6]使用镜像粒子法模拟了规则固体边界条件下流体运动。SOLENTHALER和GROSS[7]重新定义接近自由表面的粒子采样方法。SCHECHTER和BRIDSON[8]提出一种ghost方法用于模拟流体的自由表面和边界条件。BECKER和TESCHNER[9]提出泰特方程去降低不可压缩性，并且介绍利用高阻尼方程初始化粒子使镜像粒子达到稳定的密度。但是，在复杂或可变形固体边界处难以生成镜像粒子是以上镜像粒子法均存在的问题。

SOLENTHALER等[10]基于静态粒子法的思想，对固体边界进行粒子采样，并将这些粒子看作位置固定的特殊流体粒子，参与流体的物理计算过程，以保证流固交界面附近流体粒子压强和速度分布均匀。但是，在流体粒子速度较大时会出现粒子穿透固体边界的现象，因此需要使用较小的时间步长来解决此问题。DALRYMPLE和KNIO[11]通过对边界进行多层静态粒子采样，以避免流体粒子穿透固体边界。IHMSEN等[12]在静态粒子法的基础上，对穿透固体边界的粒子实施位置校正，同时在物理计算过程中加入了固体边界对流体粒子的贡献，有效避免了流固交界面附近流体粒子密度变化过大的问题。邵绪强等[13]提出一种静态粒子与位置-速度校正技术相结合的方法，解决了流体与固体边界交互时流体粒子的穿透与衰减问题；但静态粒子作为特殊的流体粒子，仍然存在边界截断所造成的误差。

在流固耦合模拟中，镜像粒子法由于其本身特性越来越受到广泛应用，但在复杂边界下却存在计算量过大、算法复杂等缺点。针对镜像粒子法的上述缺点，本文提出一种改进方法：改变镜像粒子分布、采用新的镜像粒子场量计算方法。大量实验结果表明，随着模拟粒子数和边界复杂度的提高，本文方法比传统镜像粒子法效率高的优势更加明显。

1 流固耦合算法

1.1 SPH流体

SPH方法是一种无网格拉格朗日型的粒子方法，在1977年分别由LUCY[14]与GINGOLD和MONAGHAN[15]提出，从开始用于解决三维开放空间的天体物理学问题，到目前被广泛应用于流体动力学、固体力学及其他工程学科各种问题的数值仿真。

DESBRUN和GASCUEL[16]首次将SPH方法引进图形学领域，模拟可变形固体；MÜLLER等[17]则采用SPH方法来模拟水，为该方法在模拟水等流体方面奠定了算法基础。

SPH是一种无网格插值方法，通过对离散粒子的物理属性进行插值计算，而得到连续区域内任一点处的对应值

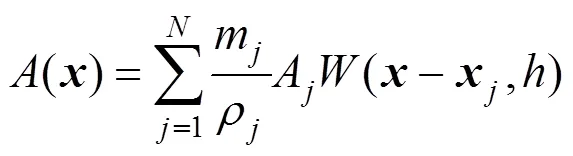
其中，()是位置处的物理属性值；为邻居粒子总数；m、、A、分别为位置处支持域范围内粒子的质量、密度、物理属性值和位置；(–,)为光滑核函数；为光滑核半径。

将式(1)应用于流体密度可得

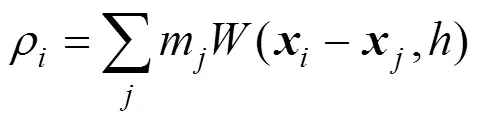
在每个时间步内，流体粒子的速度、位置等信息根据其所受合力进行计算。合力包括压力、粘性力和外力，外力为重力，即

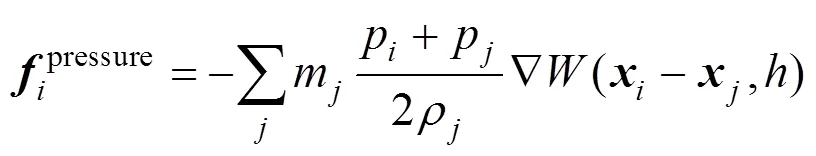
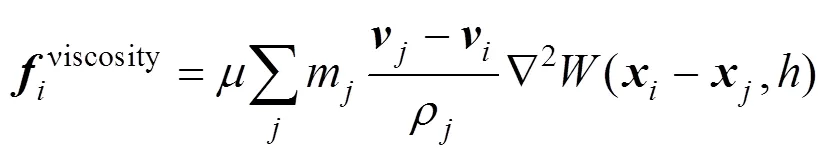
通过式(2)求得粒子密度后，需要对粒子压强进行计算，以求得粒子压力。

文献[14]使用气体状态方程式来计算粒子压强，即

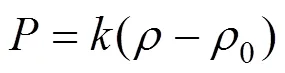
其中，为气体常数；0为常量密度。

1.2 镜像粒子法改进

传统镜像粒子法中，在每一时间步，靠近边界的流体粒子在边界外镜像生成虚拟粒子(图1)，且将靠近边界的流体粒子场量赋给相应的镜像粒子场量，即。

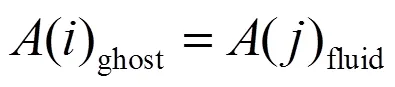
其中，j为靠近边界的流体粒子；i为对应的镜像粒子；A(i)ghost为镜像粒子i的场量；A(j)fluid为流体粒子j的场量。

因此，传统镜像粒子法在每一时间步需动态生成镜像粒子，并重新确定镜像粒子的位置，计算量有所增加。而且在复杂边界情况下，难以确定镜像粒子的位置，使得计算量和算法复杂度大大提高。

与之相反，本文提出一种固定的镜像粒子方法。首先，将提出的镜像粒子固定分布在固体边界表面的外侧，保持位置不变，分布层数与粒子影响域和粒子初始分布有关其次，为计算每个固定镜像粒子的场量，本文引入插值点这一概念，使每个固定镜像粒子都有其对应的插值点，通过计算插值点处的场量而得出固定镜像粒子的场量。每个固定镜像粒子对应插值点的位置与固定镜像粒子的位置关于固体边界相互对称(图2)。

图2 本文方法镜像粒子分布

每个固定插值点的变量由传统的SPH方法通过相邻的流体粒子获得，见式(10)。然后将插值点的场量赋值给相应的ghost粒子，见式(7)。

对于不同要求的滑移条件，对速度可采用式(8)或式(9)。

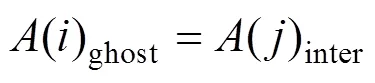
对于非滑移边界，有

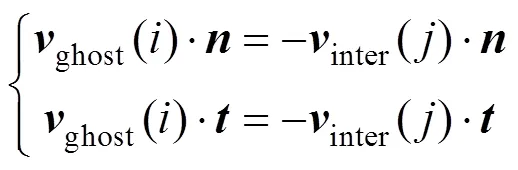
对于滑移边界，有

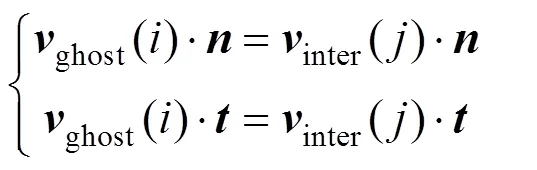
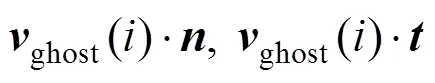
利用传统SPH方法对插值点的场量进行求解，即

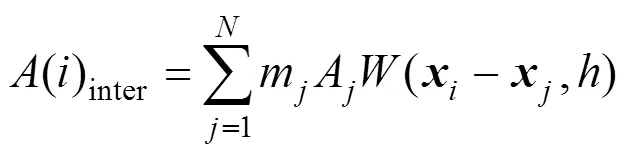
其中，为插值粒子；为领域内的流体粒子。

1.3 算法描述

本文算法如图3所示。

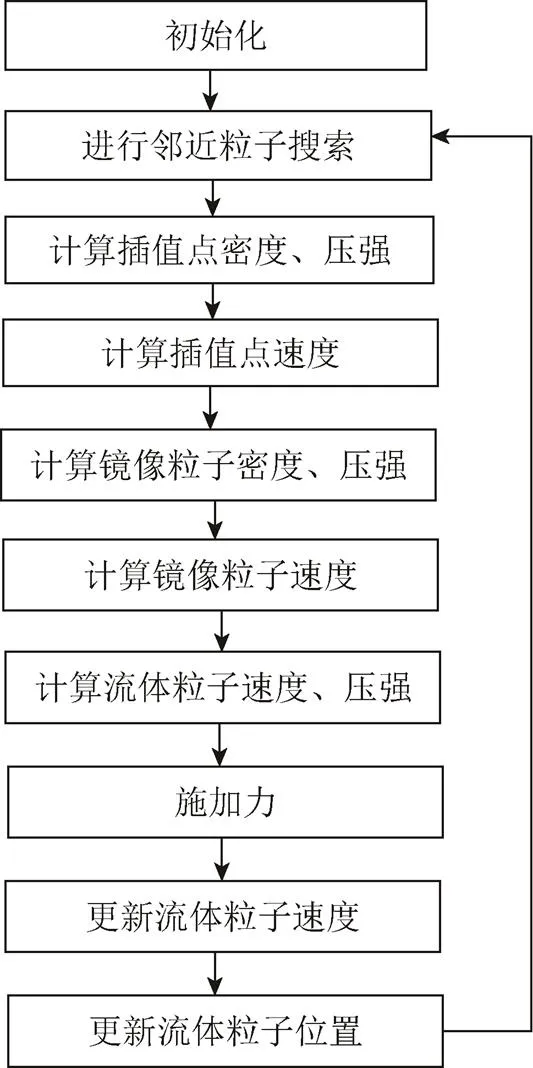
图3 本文算法流程图

仿真算法步骤如下：

步骤1. 初始化流体粒子和镜像粒子。

步骤3. 通过式(2)计算插值点密度inter，式(5)计算压强inter。

步骤4. 通过式(10)计算插值点速度inter。

步骤5. 通过式(7)~(9)得到镜像粒子密度ghost、压强ghost和速度ghost。

步骤6. 通过式(2)计算流体粒子密度，式(5)计算流体粒子压强P。

步骤7.对流体粒子施加力，即=pressure+viscosity+other。

步骤10. 重复步骤3。

2 实验

2.1 二维溃坝

溃坝是经典的自由表面流体运动模型，常用来验证壁面边界施加方法的有效性。

计算参数有：初始密度为1 000 kg/m3，边界粒子数目为292，流体粒子数目1 681，流体粒子初始间距为0.018 m，时间步长为1.0´10–3s，粒子的影响域=0.04 m。

2.1.1 本文方法与不施加边界处理相比较

由图4可知，图4(a)流体粒子不论是在固体边界还是在流体表面，粒子分布都比图4(b)更加均匀。因此，本文方法能够使粒子分布更加均匀，使场量更加稳定。

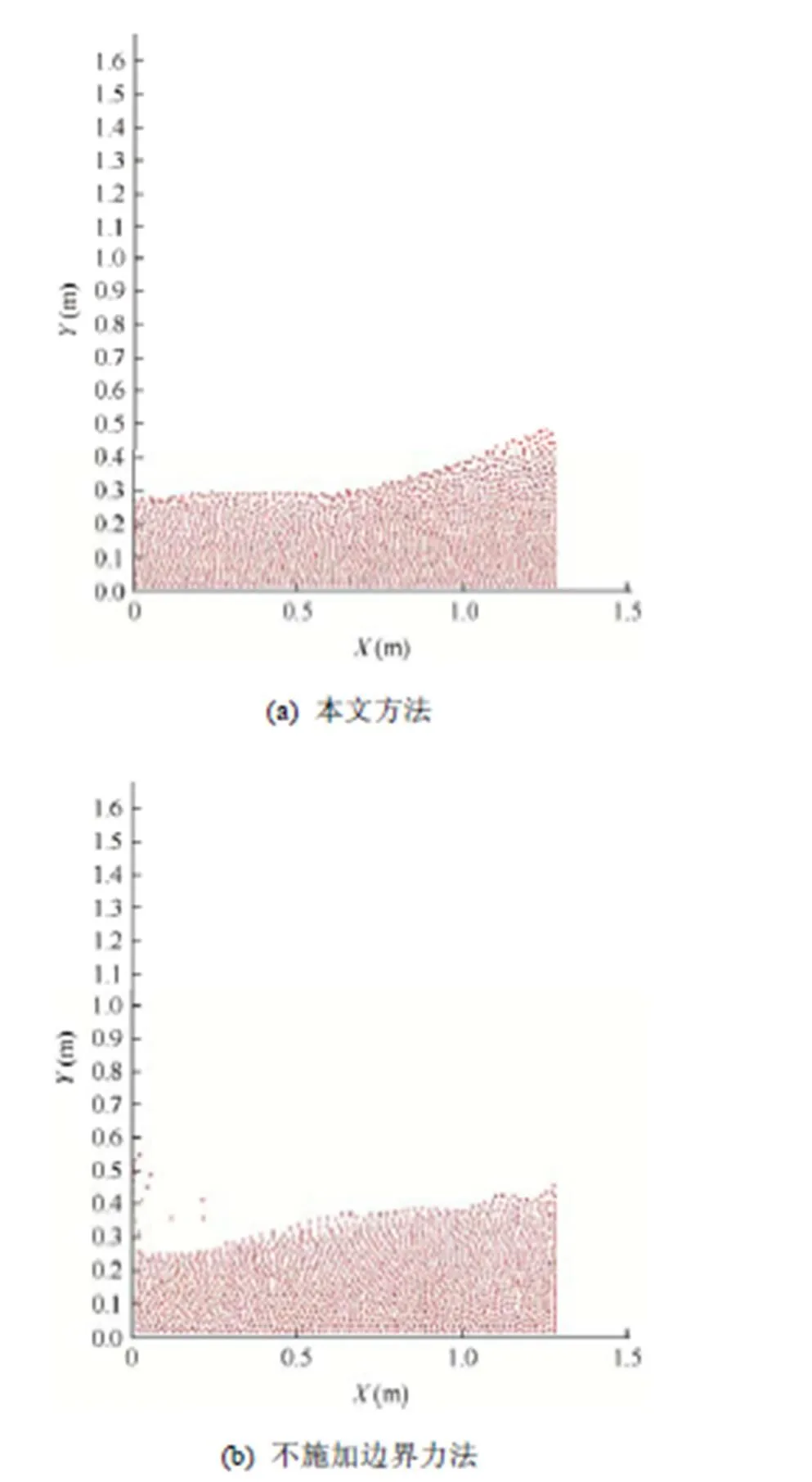
图4 本文方法与不施加边界力法比较

2.1.2 本文方法与静态粒子法相比较

由图5可知，图5(a)流体粒子在边界处没有穿透现象；图5(b)流体粒子在边界处有穿透现象。因此，本文方法比静态粒子法更有效的防止粒子渗透。

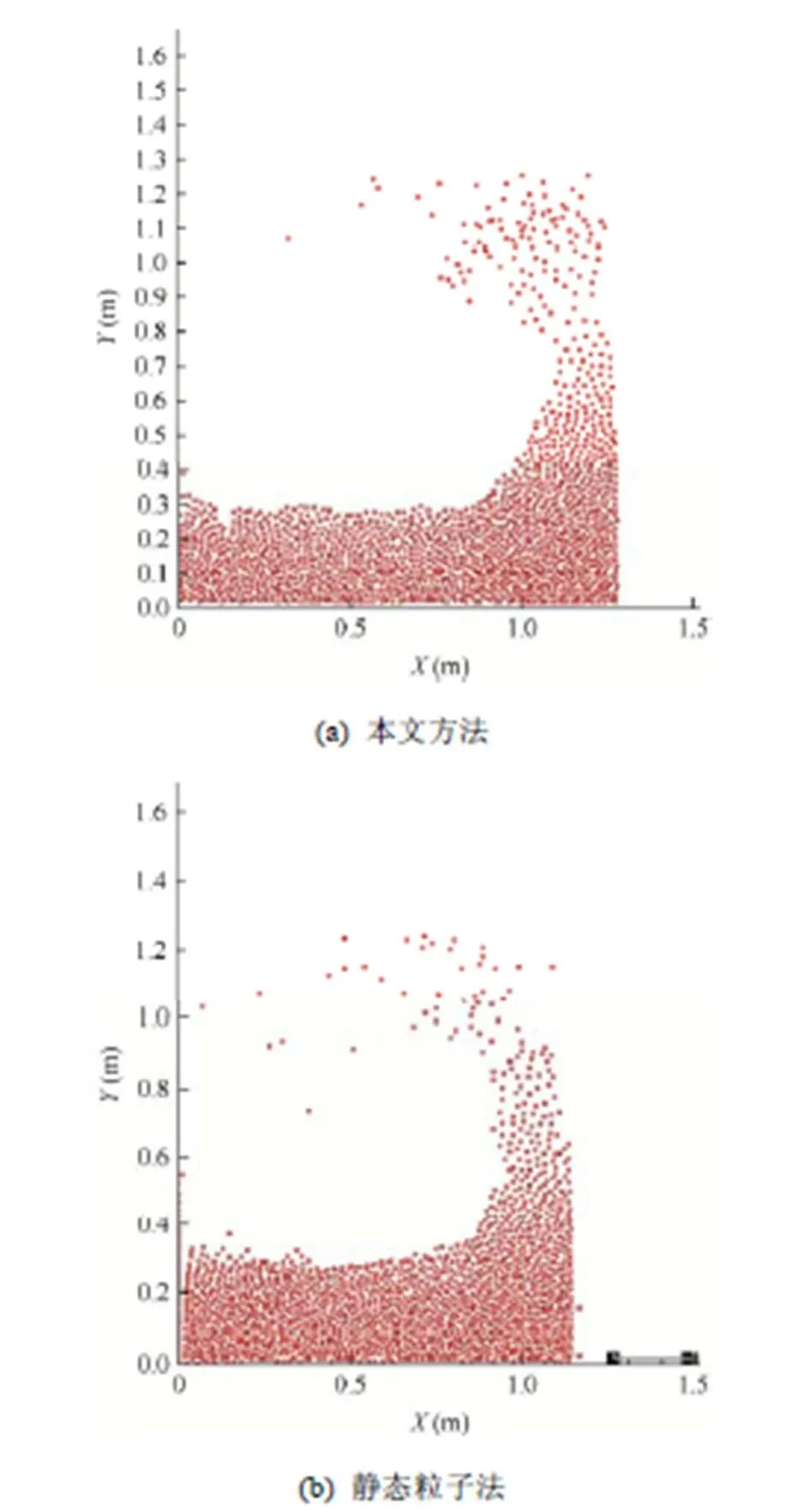
图5 本文方法与静态粒子法比较

2.2 三维溃坝

实验在Window 7平台上进行，采用visual studio 2013，cuda8.0和POV。实验环境为Intel(R) Core(TM) i5-2400 3.10 GHz CPU，4 G内存，NVIDIA Geforce GT 620显卡。

由图6~9可以看出，本文方法能够有效模拟各种复杂边界下的流体运动；由表1~4可知，随着边界复杂程度的提高和模拟粒子数的增加，本文方法的耗时比镜像粒子法耗时短的效果更加明显。

图6 本文方法与镜像粒子法比较1

图7 本文方法与镜像粒子法比较2

图8 本文方法与镜像粒子法耗时比较3

图9 本文方法与镜像粒子法耗时比较4

表1 本文方法与镜像粒子法耗时比较1

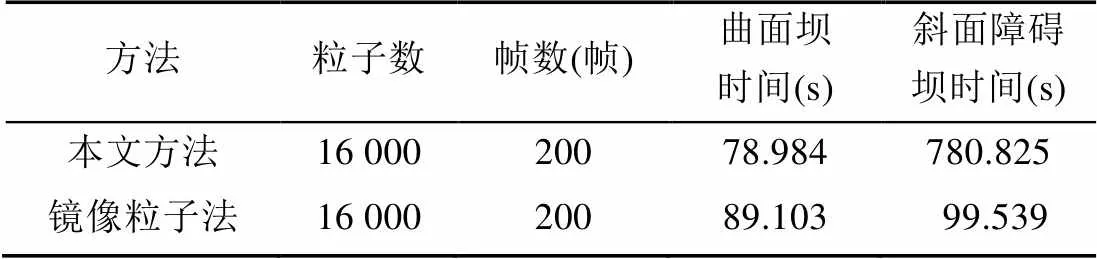
表2 本文方法与镜像粒子法耗时比较2

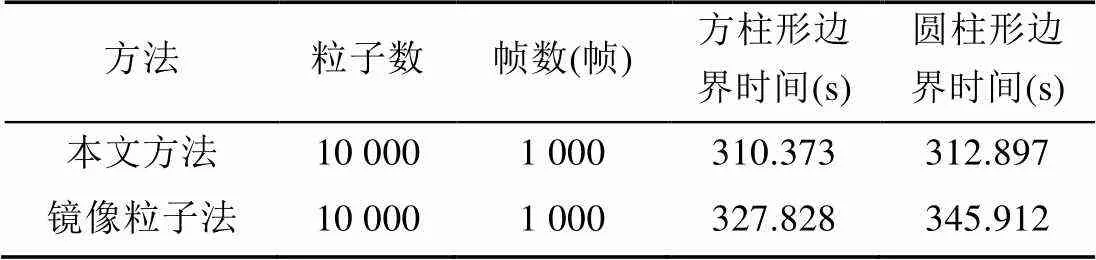
表3 本文方法与镜像粒子法耗时比较3

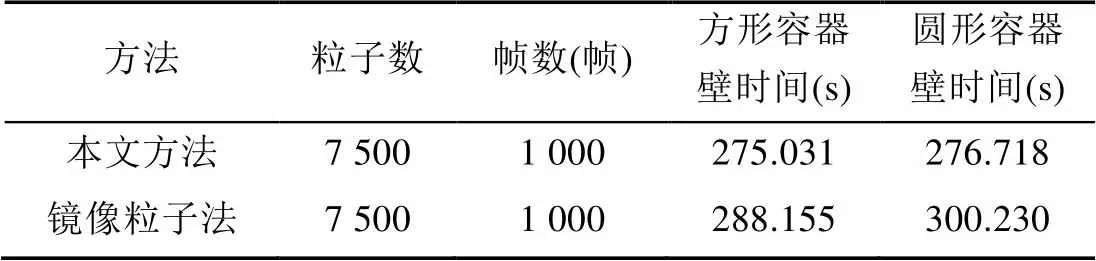
表4 本文方法与镜像粒子法耗时比较4

3 结 论

本文基于SPH方法提出一种新的流固边界处理算法，给出一种虚拟粒子场量新的求值方法，大大降低了处理边界的复杂程度；随着模拟粒子数和边界复杂度的提高，本文方法比传统镜像粒子法效率高的优势更加明显。

本文方法渲染效果未能达到满意程度，是受当前硬件限制和软件条件，后期将进行相关改进。此外，在容器较大、流体运动比较平缓的情况下，预先固定镜像粒子将造成一定的浪费。因此，接下来将对这两方面进行改进。

[1] MONAGHAN J J. Simulating free surface flows with SPH [J]. Journal of Computational, 1994, 110(2): 399-406.

[2] MONAGHAN J J, PRICE D J. Toy stars in one dimension [J]. Monthly Notices of the Royal Astronomical Society, 2004, 350(4): 1449-1456.

[3] MÜLLER M, SCHIRM S, TESCHNER M. Interaction of fluids with deformable solids [J]. Journal of Visualization and Computer Animation, 2004, 15(3-4): 159-171.

[4] BECKER M, TESSENDORF H, TESCHNER M. Direct forcing for lagrangian rigid-fluid coupling [J]. IEEE Transactions on Visualization and Computer Graphics, 2008, 15(3): 493-503.

[5] HARADA T, KOSHIZUKA S, KAWAGUCHI Y. Real-time fluid simulation coupled with cloth [C]//Theory and Practice of Computer Graphics. Coslar: Eurographics Press, 2007: 13-18.

[6] HU X Y, ADAMS N A. Amulti-phase SPH method for macroscopic and mesoscopic flows [J]. Journal of Computational Physics, 2006, 213(2): 844-861.

[7] SOLENTHALER B, GROSS M. Two-scale particle simulation [J]. ACM Transactions on Graphics (TOG), 2011: 30(4): 1-8.

[8] SCHECHTER H, BRIDSON R. Ghost SPH for animating water [J]. ACM Transactions on Graphics (TOG), 2012, 31(4): 61.

[9] BECKER M, TESCHNER M. Weakly compressible SPH for free surface flows [C]//ACM SIGGRAPH/Eurographics Symposium on Compute Animation. New York: ACM Press, 2007: 209-217.

[10] SOLENTHALER B, SCHLAFLI J, PAJAROLA R. A unified particle model for fluid-solid interaction [J]. Computer Animation and Virtual Worlds, 2007, 18(1): 69-82.

[11] DALRYMPLE R A, KNIO O. SPH modelling of water waves [C]//Proceedings of the Fourth Conference on Coastal Dynamics. New York: ACM Press, 2000: 779-787.

[12] IHMSEN M, AKINCI N, GISSLER M, et al. Boundary handling and adaptive time-stepping for PCISPH [C]//Proceedings of the Seventh Workshop on Virtual Reality Interactionsand Physical Simulations. Switzerland: Eurographics Association Press, 2011: 79-88.

[13] 邵绪强, 周忠, 张劲松. 微可压缩SPH流体的稳定性固体边界处理算法[J]. 计算机辅助设计与图形学学报, 2014, 26(11): 1915-1922.

[14] LUCY L B. A numerical approach to the testing of the fission hypothesis [J]. The Astronomical Journal, 1977, 82(82): 1013-1024.

[15] GINGOLD R A, MONAGHAN J J. Smoothed particle hydrodynamics: theory and application to non-spherical stars [J]. Monthly Notices of the Royal Astronomical Society, 1977, 181(3): 375-389.

[16] DESBRUN M, GASCUEL M P. Smoothed particles: a new paradigm for animating highly deformable bodies [C]//EGCA: Proceedings of the 1996 Eurographics Workshop on Computer Animation and Simulation. Berlin: Springer, 1996: 61-76.

[17] MÜLLER M, CHARYPAR D, GROSS M. Particle-based fluid simulation for interactive applications [C]// Proceedings of the ACM SIGGRAPH/Eurographics Symposium on Compute Animation. Switzerland: Eurographics Association Press, 2003: 154-159.

An Improved Solid Boundary Treatment Algorithm of Fluid Simulation

ZHU Xiaolin, YIN Jingcun, WANG Huanhuan

(School of Mathematics, Hefei University of Technology, Hefei Anhui 230009, China)

Fluid simulation is an important research branch of computer graphics, solid boundary treatment of fluid has always been the focus of fluid simulation, image particle method in smooth particle hydrodynamics is an important method to deal with solid boundary. Image particle method deals with solid boundary problems by dynamically generating corresponding mirror particles outside the boundary by fluid particles near the boundary. However, with the improvement of the complexity of the boundary, the complexity of the traditional mirror particle method to generate the mirror particles is also increased, and the simulation efficiency is reduced. In order to solve the above problem, the mirror particle method is improved in this paper by giving a new technique for calculating values of mirror particle field, which effectively reduces the complexity of the generation of traditional mirror particles with complex boundary conditions, and the field of fluid particles near the boundary is more uniform. A lot of simulation results show that this method becomes more efficient compared with the mirror particle method with the increasement of the number of particles and the complexity of the scene.

smoothed particle hydrodynaimics method; fluid simulation; solid boundary treatment; ghost particle field; complex scene

TP 391.9

10.11996/JG.j.2095-302X.2018020263

A

2095-302X(2018)02-0263-06

2017-06-22；

2017-11-08

国家自然科学基金项目(61272024)

朱晓临(1964–)，男，安徽池州人，教授，博士。主要研究方向为数值逼近、CAGD、图形图像处理。E-mail：zxl_hfut@126.com