大气层外反TBM拦截弹变结构末制导律研究
2018-05-08臧月进李仁俊安国琛
臧月进,李仁俊,安国琛
(上海机电工程研究所,上海,201109)
0 引 言
大气层外飞行的动能拦截器(KKV)采用直接碰撞方式,利用巨大的动能来拦截弹道导弹弹头[1]。在中段发动机燃料耗尽关机自由滑行后,当中、末制导交班结束时,目标进入了KKV导引头的作用范围,并被导引头捕获进入末制导阶段,被拦截的目标为处于自由段飞行的弹道导弹弹头[2]。在末制导段,KKV采用捷联红外成像导引头测量与目标的相对位置,实现该段的制导控制。末制导段是整个拦截任务成功与否最后关键一步。
由于拦截问题与交会问题不同(交会问题要求在交会时刻,追踪航天器和目标的相对位置和相对速度同时达到0),在拦截问题中,不需要进行纵向制导,只需要在拦截阶段给拦截弹提供一个冲量,让拦截弹获得一个较大的速度,依靠动能去杀伤目标。而法向制导和横向制导的目的是捕捉逼近走廊,并抑制视线转动[3]。
为了抑制视线转动,最好采用比例导引法,而采用常推力多次启动的发动机控制,发动机开启时产生的加速度是常值,且当拦截器与目标接近时发动机频繁开关机[3],特别当目标机动,其法向过载接近甚至强于拦截器法向过载能力时,其性能会大大下降,终端脱靶量很大[4]。但比例法导引过程中所需要的加速度是随视线转动而变化的,因此只能利用由比例导引法所确定的导引曲线作为发动机开关线。
经典的比例导引法是介于追踪法和平行接近法之间的制导方法,对于拦截非机动目标时,弹道性能好、脱靶量小、易于工程实现。然而如果弹道式导弹TBM弹头存在机动,比例导引法的性能会大大下降,拦截弹的法向过载过早饱和,造成终端脱靶量大。基于现代控制理论设计的具有滑动模态的变结构控制系统对系统的不确定因素有较强的稳定性和抗干扰性[5-7],对目标机动和制导参数变化具有自适应性,可以通过滑动模态的设计获得令人满意的动态品质,并且有几乎同比例导引律一样应用简单的特点[8],满足拦截机动目标对导引律的要求。
文献[5]采用滑模变结构导引律设计了KKV分别采用追击和迎击方式对TBM的拦截,同时为了减少高频颤振,采用饱和函数代替符号函数;文献[9]采用模糊逻辑的滑模制导律,其视线角速率和脱靶量较小。但是,他们均不具备对弹头机动时的有效拦截。
为了对付具备一定机动能力的TBM弹头,需设计出一种新型的具有工程实用价值的导引规律。
1 拦截过程相对运动学模型
选择某一时间区间Δt起始时刻的视线坐标系Dξηζ作为末制导过程的相对运动参考系。末制导过程中的相对运动可以解耦成纵向平面Dξ η和侧向平面Dξ ζ内的运动。
以纵向平面Dξ η内的运动为例,设在Δt内,视线高低角的增量为ε,则
(1)
式中:ρ(t)表示拦截弹与目标之间的相对距离,η(t)表示Δt时间内Dη方向上的相对位移。若时间区间Δt足够小,则ε(t)是一个很小的量。因此
(2)
式(2)对时间t微分一次,得到
(3)
把η(t)=ρ(t)ε(t)代入到式(3)得
(4)
式(4)对时间t再微分一次,得到
(5)
把式(4)代入到式(5),得到
(6)
式中:
amη(t)、atη(t)分别表示拦截弹和目标机动加速度在Dη方向上的分量。
(7)
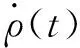
(8)
2 自适应滑模变结构制导律设计
为了使动力学系统对干扰和目标机动具有鲁棒性,本文变结构制导律滑动模态取为
s=ρ(t)x(t)
(9)
为了保证系统状态能够到达滑模,而且到达滑模的过程中有优良的动态特性,可以运用趋近律来推导控制器。这里令动力学系统的自适应滑模趋近律为
(10)
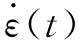
因为ρ(t)>0,得到
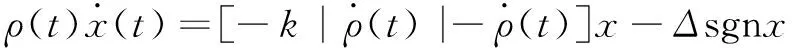
(11)
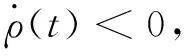
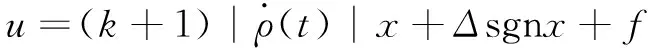
(12)
在实际应用中,目标的机动加速度可能无法得到,因此容易实现的适应滑模制导律为
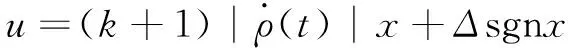
(13)
(14)
将控制量代入到式(14),得到
(15)

V(t)→0,t→∞
(16)
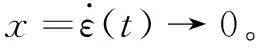
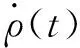
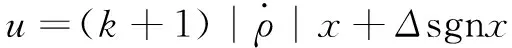
(17)
式(17)含有开关函数项,要求控制量进行切换。在实际系统中,控制量的切换不可能瞬时完成,总存在一定的时间滞后,这会造成抖动。为了消除控制量的切换造成的抖动,可以对非连续开关函数进行光滑处理,经过平滑处理后的制导律为
(18)
其中,δ为小正数。
同样,也可以推导出侧向平面内的自适应滑模变结构制导律。
如果拦截弹上的姿态控制系统令其俯仰角ϑ跟踪视线高低角ε(t),偏航角ψ跟踪视线方位角β(t),那样,弹体坐标系O1x1y1z1与视线坐标系Dξηζ重合,综合以上过程,得到三维空间中的制导律为

(19)

从上式可见,该制导律的第一项为常规的比例导引律,第二项为针对目标弹头机动设计的滑模项,且具备一定的光滑特性。
按式(19)实现的制导律,要求拦截弹的轨控发动机提供的加速度是时变的,但拦截弹轨控采用的是推力大小固定、能多次启动的发动机来控制[10],开启时产生的加速度是常值,可以按冲量等价的原则进行脉宽调制。
3 末段导引弹道仿真分析
3.1 TBM弹头机动模型
为提高弹道导弹突防概率,往往在中末段有一段弹道机动过程,如美国的“潘兴”导弹再入段就有俯冲后拉起的机动过程[11]。
通过将TBM弹头设计成气动布局为不对称,弹头再入高速经过大气层时,气动升力很大,会产生配平攻角和滚动干扰力矩而形成慢速自旋时的质心螺旋机动[9],而螺旋机动将会使弹头偏离原预测的弹道式标准弹道轨迹,该螺旋机动可近似为如式(20)的解析形式[8]:
(20)
式中:vT为目标速度;B为弹道系数;gT为重力加速度;ny2为弹道法向过载;ωx1T为弹体绕纵轴的自旋角速度;b为滚动阻尼系数;c为滚动干扰力矩系数;γT为弹体自旋角;θT、φT分别为目标的速度倾角和偏航角;ρa为空气密度;xT、yT、zT为目标坐标。
3.2 仿真范例
某样例拦截器的质量为20 kg,轨控发动机推力为F=490 N。
在末制导导引启动时刻,TBM运动如3.1节所述,其与KKV在发射惯性系下初始位置/速度如表1所示。
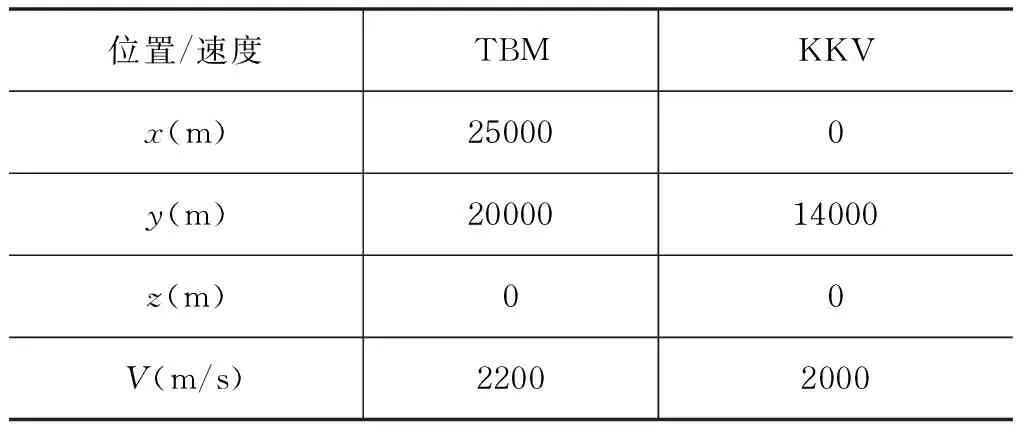
表1 启导时刻弹目相对位置和速度
拦截过程仿真如图1~图3所示。
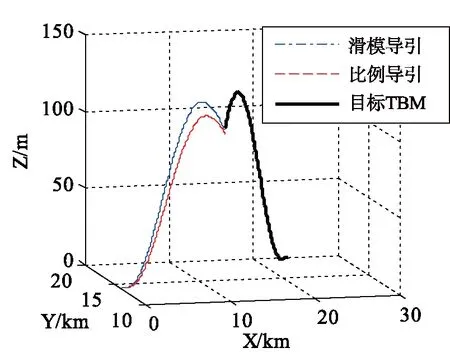
图1 发射惯性系下的弹目相对位置Fig. 1 Interceptor and target trajectories
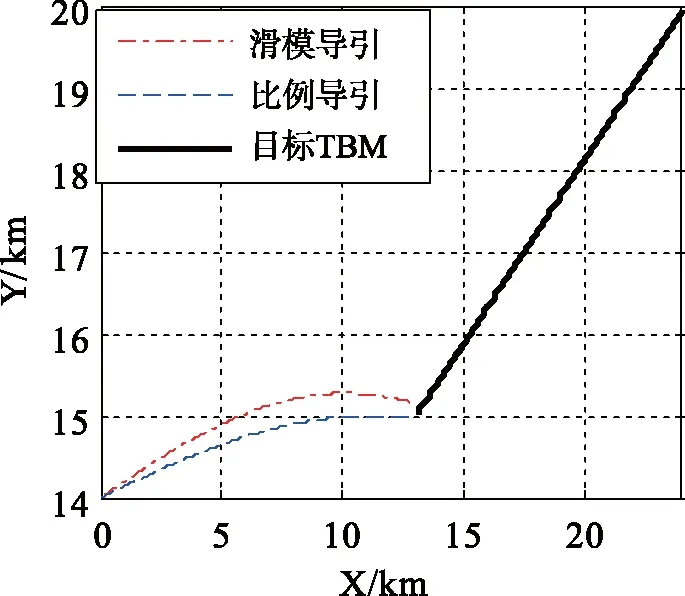
图2 拦截平面XOY侧视图Fig. 2 XOY intercept plane
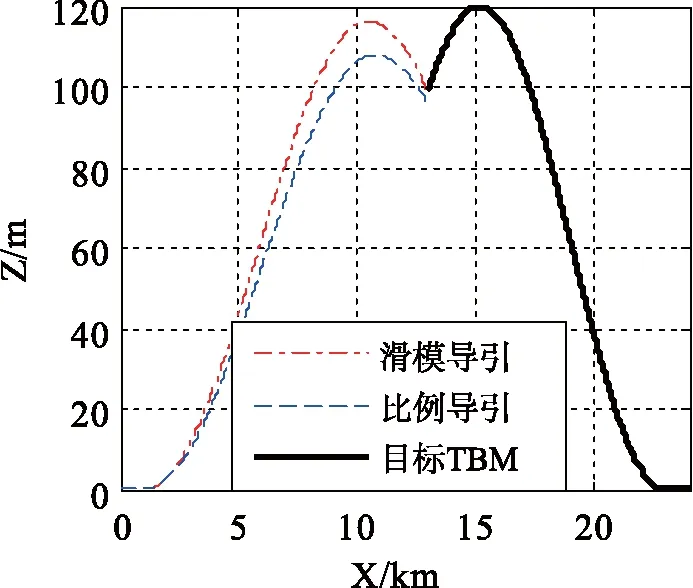
图3 拦截平面XOZ俯视图Fig. 3 XOZ intercept plane
从上述仿真拦截过程的空间位置变化可以看出,本文自适应滑模变结构制导律能快速响应目标跟踪过程;从终端脱靶量对比看,采用本文自适应滑模变结构制导律的脱靶量为0.057 1 m,比比例导引律脱靶量0.753 m小一个数量级。滑模变结构制导律对应的四轨控推力如图4所示。
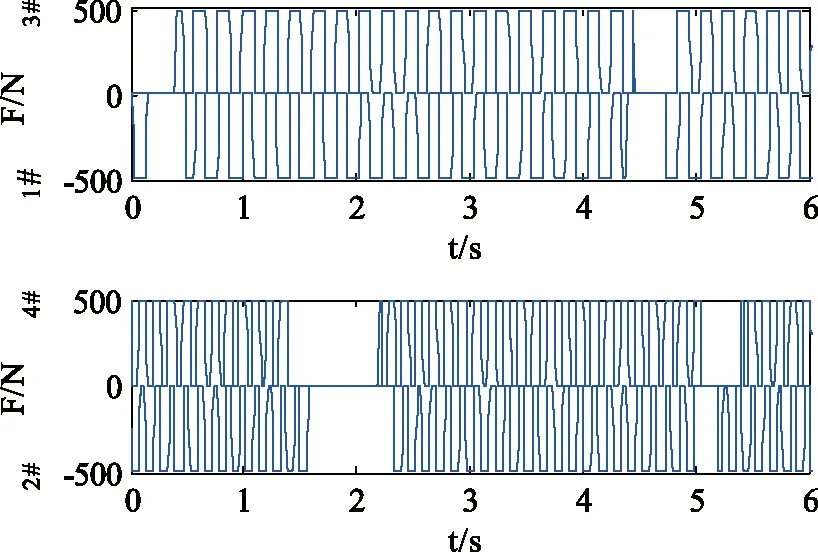
图4 滑模变结构制导轨控发动机开机曲线Fig. 4 On-off curve of divert control thrust
从图4可见,整个拦截过程中4个阀门一致处于高速的切换过程中,这是由于目标螺旋机动,引起拦截弹相应的机动调整。
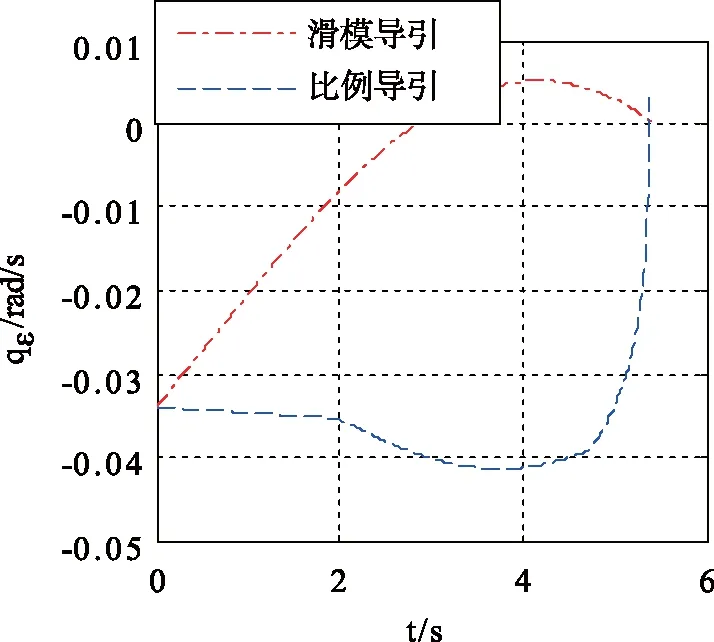
图5 纵向视线角速率对比曲线Fig. 5 Rates of line-of-sight elevation angle
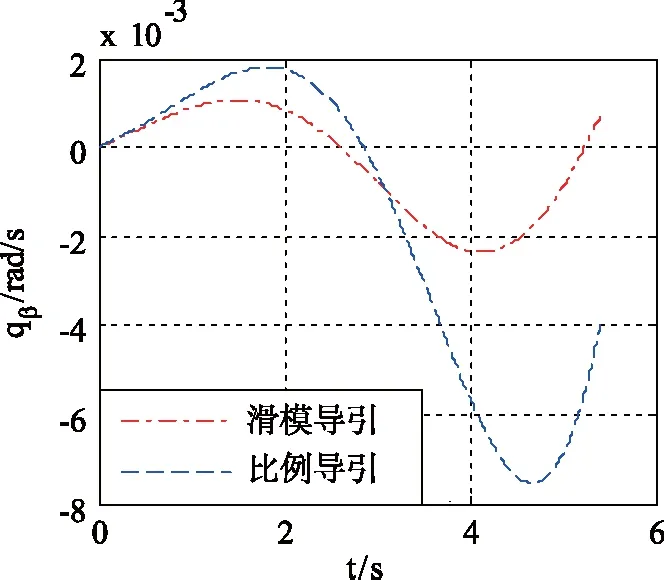
图6 横向视线角速率对比曲线Fig. 6 Rates of line-of-sight azimuth angle
从图5和图6视线角速率可见,相较于比例导引律,本文设计的自适应滑模变结构制导律在启导阶段视线角速率幅值变化较大,而后逐步变小。
通过以上仿真对比分析,采用本文自适应滑模变结构制导律的制导精度高于比例导引制导律的制导精度,动态响应品质更优。
4 结束语
本文基于变结构理论采用指数趋近率设计的滑模变结构制导律,经仿真验证,对KKV拦截TBM作突防机动时有很好的鲁棒性和较低的脱靶量,验证了自适应滑模变结构制导律导引KKV打击TBM机动弹头的能力。
[1] 黄万伟.动能拦截器变结构自动驾驶仪设计方法研究[J].航天控制,2004,22(2):16-18.
[2] 田源,任章.大气层外动能拦截器末段导引规律设计[J].宇航学报,2009,30(2):474-480.
[3] 张雅声,程国采,陈克俊.高空动能拦截器末制导导引方法设计与实现[J].现代防御技术, 2001,29(2):31-34.
[4] 周荻.寻的导弹新型导引规律[M].北京:国防工业出版社,2002:2-3.
[5] 闫宝琴,金玉华,李君龙.滑模变结构导引律在动能拦截器上的应用研究[J].现代防御技术,2008, 36(1):14-19.
[6] 曹开田.滑模变结构控制理论在飞行器姿态控制系统中的应用研究[R].武汉大学,2004.
[7] Brierley SD, Longchamp R.Application of Sliding-Mode Control to Air-Air Interception Problem[J].IEEE Transactions on Aerospace and Electronis Systems,1990,26(2):306-325.
[8] 张建伟,韩朝超,黄树采.基于零化脱靶量的滑模变结构制导律研究[J].战术导弹技术,2010(2):69-72.
[9] 王志清,李小兵,卓启明.智能滑模变结构制导律[J].上海航天,2011(1):32-36.
[10] Ongki Moon,Kiseok Kim,Youdan Kim.Design of Missile Na-vigation Law via Variable Structure Control[J].Journal of Na-vigation,Control and Dynamics.2001,24(4):659-664.
[11] 郦苏丹,任萱,吴瑞林.再入弹头的螺旋机动研究[J].宇航学报,2000(10):41-48.
