引入分系统优化的协同优化方法及其应用研究
2018-05-08卫晓娜徐海斌陈金强董云峰
卫晓娜,徐海斌,陈金强,董云峰
(1. 中国科学院空间应用工程与技术中心,北京,100094;2. 哈尔滨飞机工业集团有限责任公司,哈尔滨,150066;3. 北京航空航天大学宇航学院,北京,100191)
0 引 言
协同优化方法(Collaborative Optimization, CO)将复杂系统优化问题分解成系统级优化和学科级优化[1],因高度的学科自治性,广泛应用于卫星[2]、火箭[3]、飞机[4]、潜艇[5]等复杂工程系统的设计。Huang等[2]以分系统对共享设计变量的优化结果与系统级期望取值差异最小为目标对控制、电源、结构等多个分系统进行优化,Cao等[5]以流体力学、推进、重量、性能和成本等学科优化结果与系统级期望值差异最小对潜艇进行初步概念分析。可见,传统CO方法分系统级的优化目标是分系统优化方案与系统级提议的目标方案差异最小[6,7],没有进行分系统优化,不能保证分系统自身最优,因此不能保证协同优化方法结果最优。针对这个问题,本文提出了引入分系统优化的协同优化方法,并通过卫星总体设计验证了方法的有效性。
1 传统协同优化方法
传统协同优化方法分为系统级优化和分系统级优化两部分,系统级优化的目的是系统整体目标最优,同时采用等式约束保证不同学科之间共享变量的一致性。分系统级需满足本学科的约束,优化目标是使分系统优化方案与系统级提议的目标方案一致。通过系统级和分系统级间的多次迭代,最终找到一个系统级最优并且共享变量取值一致的优化结果[1]。
由图1可见,分系统没有进行分系统自身优化,不能保证分系统的最优性,另外,当分系统优化目标与系统级优化目标存在关联时,系统级优化效率低。在分系统级引入自身优化,可以改善上述两个问题。
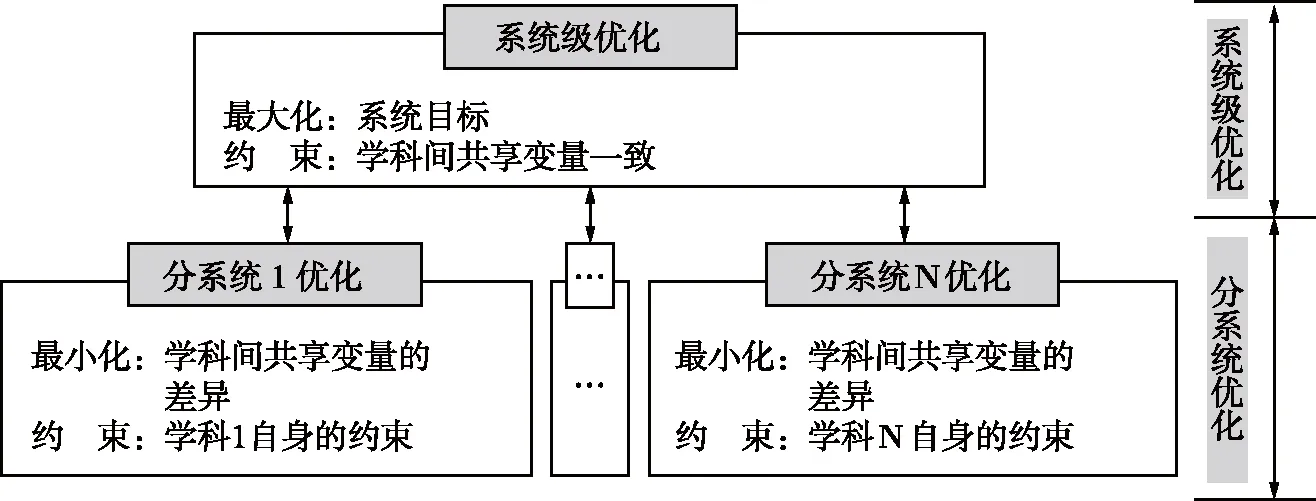
图1 协同优化设计基本框架Fig.1 The basic framework of collaborative optimization
2 引入分系统优化的协同优化方法
本文将分系统优化目标扩展为分系统自身最优并且共享变量取值与系统级提议值最接近,提出引入分系统优化的协同优化方法,如图2所示。分系统优化时既保证自身目标最优,又尽可能缩减共享变量取值的差异,分系统优化是一个多目标优化问题。
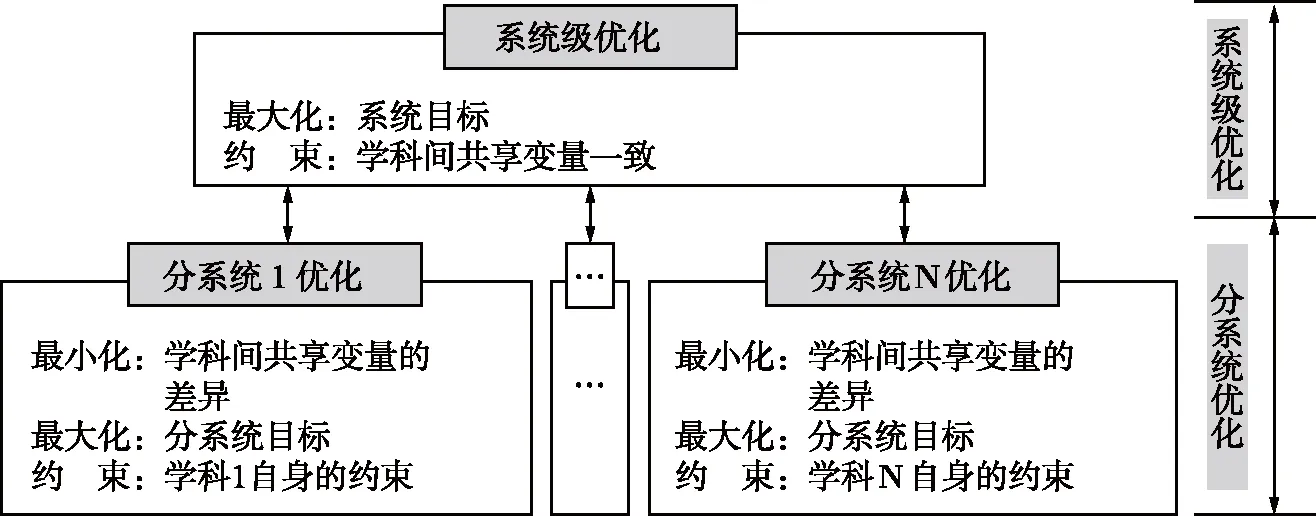
图2 引入分系统优化的协同优化方法Fig.2 Collaborative optimization method by introducing subsystem optimization
传统协同优化方法分系统级的优化模型如公式(1)所示:

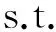
(1)
(i=1,2,…,s;j=1,2,…t)
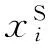


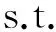
(2)
(i=1,2,…,s;j=1,2,…t)
由公式(2)可见,分系统优化目标中考虑了分系统本身最优。
3 基于卫星总体设计的优化研究
本节首先介绍了卫星总体优化模型,然后采用传统协同优化方法和引入分系统优化的协同优化方法对卫星总体优化模型进行优化,验证改进方法的有效性。
3.1 卫星总体优化模型
3.1.1 卫星总体优化系统级模型
为了验证引入分系统优化的协同优化方法的有效性,本文对包含7个分系统的卫星总体优化模型进行优化研究。系统级优化模型为:
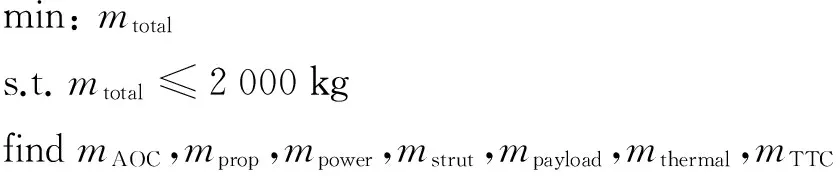
(3)
式中:mtotal为卫星总质量,mAOC为姿态与轨道控制分系统质量,mprop为推进分系统质量,mpower为电源分系统质量,mstrut为结构分系统质量,mpayload为有效载荷分系统质量,mthermal为热控分系统质量,mTTC为测控分系统质量。
3.1.2 卫星总体优化分系统级模型
a) 姿态与轨道控制分系统优化模型
姿态与轨道控制分系统优化模型如公式(4)所示:
find:xi={h,As,Asa,Iz,Iy,θa,Tstab,Tunload}
minmAOC,PAOC
(4)
s.t.mAOC≤120kg
其中,h为轨道高度,As为星体截面积,Asa为太阳电池阵面积,Iz为绕z轴的转动惯量,Iy为绕y轴的转动惯量,均为共享设计变量。θa为指向精度,Tstab为三轴稳定方式,Tunload为动量卸载方式,是局部设计变量。姿态与轨道控制分系统优化时,通过同时优化共享设计变量和局部设计变量,使姿态与轨道控制分系统的质量mAOC和功耗PAOC最小以及共享变量h、Asect、Asa、Iz、Iy的取值最接近系统级提议的目标值。其中,下标“e”表示系统级提议的目标值。设计变量取值范围如表1所示。
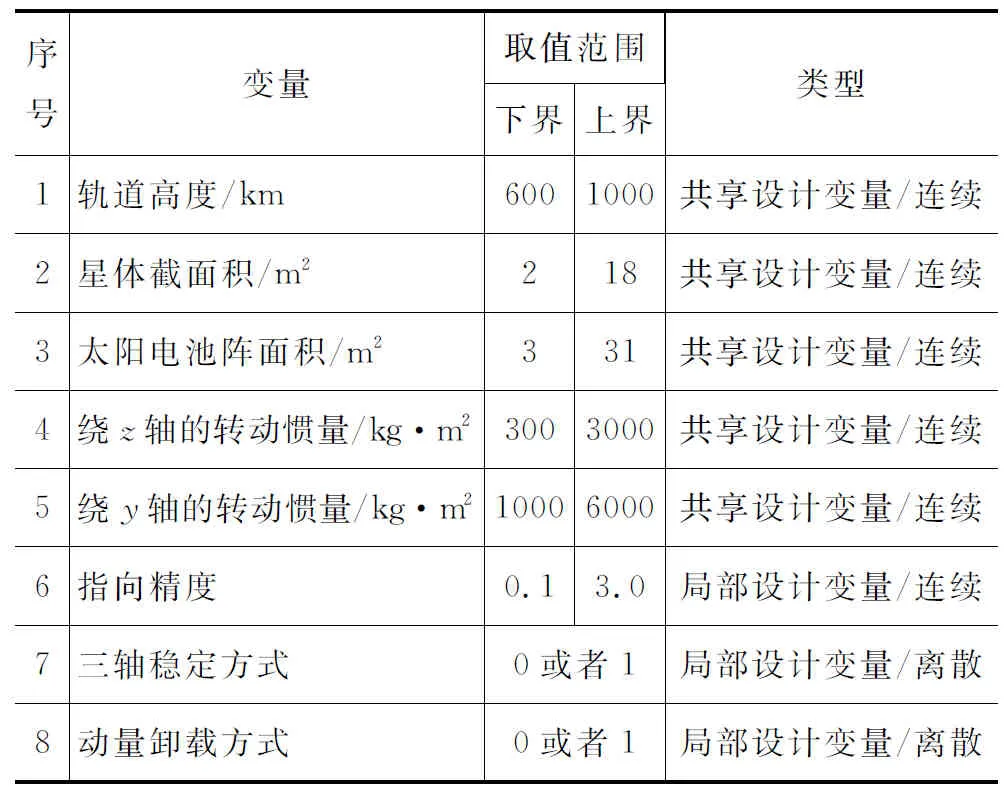
表1 姿态与轨道控制分系统设计变量取值范围
b) 推进分系统优化模型
推进分系统优化模型如公式(5)所示:
find:xi={h,mtotal,As,Asa,Lt,Tprop}
minmprop,Pprop

(5)
s.t.mp≤300 kg
其中,轨道高度h、卫星总质量mtotal、卫星截面积As、太阳电池阵面积Asa、卫星设计寿命Lt为共享设计变量,推进剂类型Tprop为局部设计变量。优化目标是质量mprop和功率Pprop最小,共享变量h、mtotal、As、Asa和Lt最接近系统级提议的目标值。设计变量取值范围如表2所示。
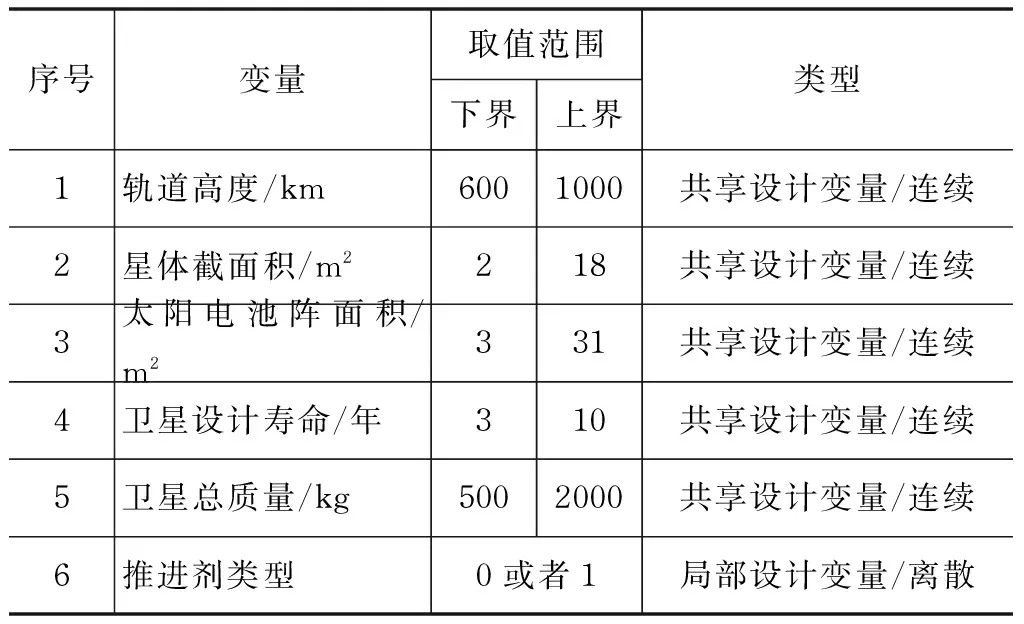
表2 推进分系统设计变量取值范围
c) 电源分系统优化模型
电源分系统优化模型如公式(6)所示:
find:xi={h,Ptotal,Lt,TSA,TBA}
minmpower,Asa,msa
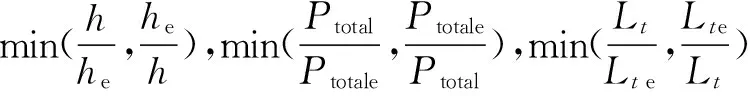
s.t.mpower≤330 kg
msa≤100 kg
(6)
AsaPEOL-(1+5%)Ptotal≥0
其中,轨道高度h、卫星功率需求Ptotal、卫星设计寿命Lt是共享设计变量;太阳电池类型TSA和蓄电池类型TBA是局部设计变量。优化目标是电源分系统的质量mpower、太阳电池阵面积Asa和太阳电池阵质量msa最小以及共享变量h、Ptotal、Lt最接近系统级提议的目标值。设计变量取值范围如表3所示。
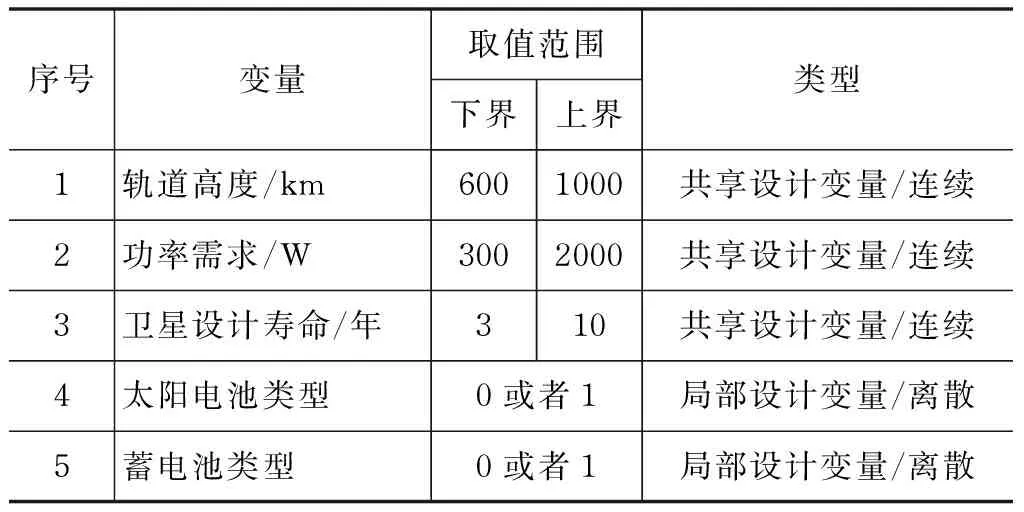
表3 电源分系统设计变量取值范围
d) 结构分系统优化模型
结构分系统优化模型如公式(7)所示:
find:xi={mtotal,mother,TSM,r,hm,tplate,Dcell,tcell}
minmstr
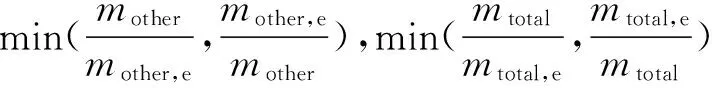
s.t.mstr≤300kg
(7)
faxial≥25Hz
flateral≥24Hzσeq≤σy
σe≤σc
其中,卫星总质量mtotal和其他分系统总质量mother是共享设计变量;材料类型TSM、横截面包络半径r、卫星结构高度hm和中心承力筒直径Dcell是局部设计变量。优化目标是在满足刚度(频率)、强度和稳定性要求下,达到结构分系统质量mstr最低,共享变量mtotal和mother最接近系统级提议的目标值。设计变量取值范围如表4所示。
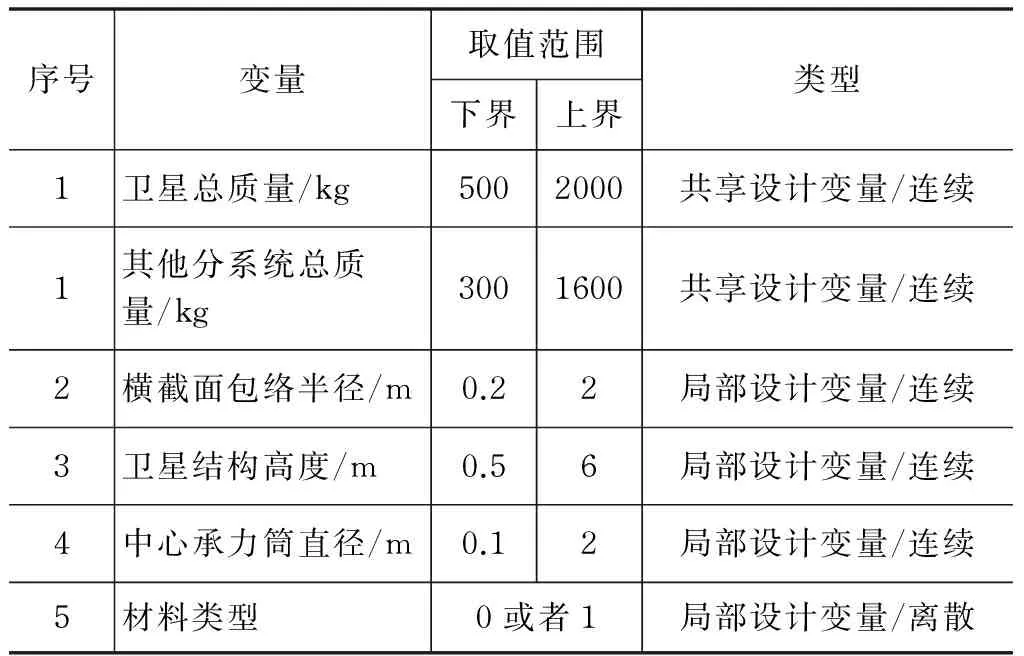
表4 结构分系统设计变量取值范围
e) 有效载荷分系统优化模型
有效载荷分系统优化模型如公式(8)所示:
find:xi={h,μ0,fc}
minmpayload,Ppayload
(8)
s.t.mpayload≤600kg
其中,轨道高度h是共享设计变量;像元尺寸μ0和相机的镜头焦距fc是局部设计变量。优化目标是有效载荷分系统质量mpayload和功率Ppayload最小,共享变量h最接近系统级提议的目标值。设计变量取值范围如表5所示。
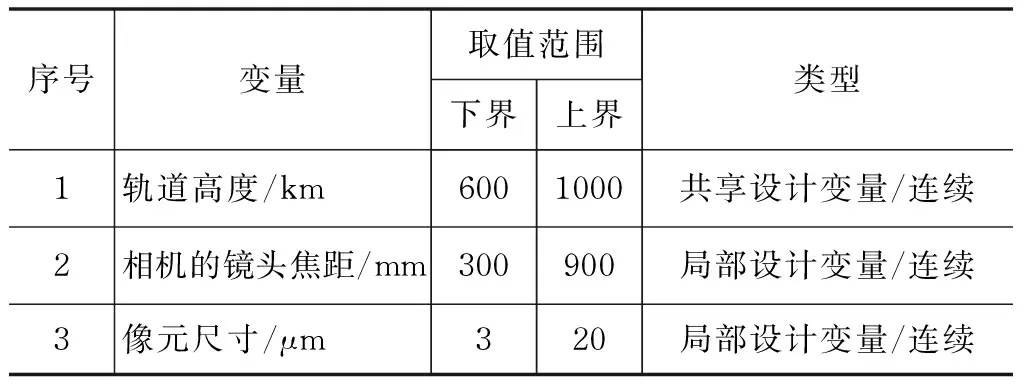
表5 有效载荷分系统设计变量取值范围
f) 热控分系统优化模型
热控分系统优化模型如公式(9)所示:
find:xi={h,Ph,δi,A7,THRM}
minmThermal,PThermal
(9)
其中,卫星轨道高度h、卫星内部热功耗Ph是共享设计变量;卫星各表面隔热涂层厚度δi、散热窗面积A7和隔热材料类型THRM是局部设计变量。优化目标是质量mThermal和功率PThermal最小,共享变量h和Ph最接近系统级提议的目标值。设计变量取值范围如表6所示。
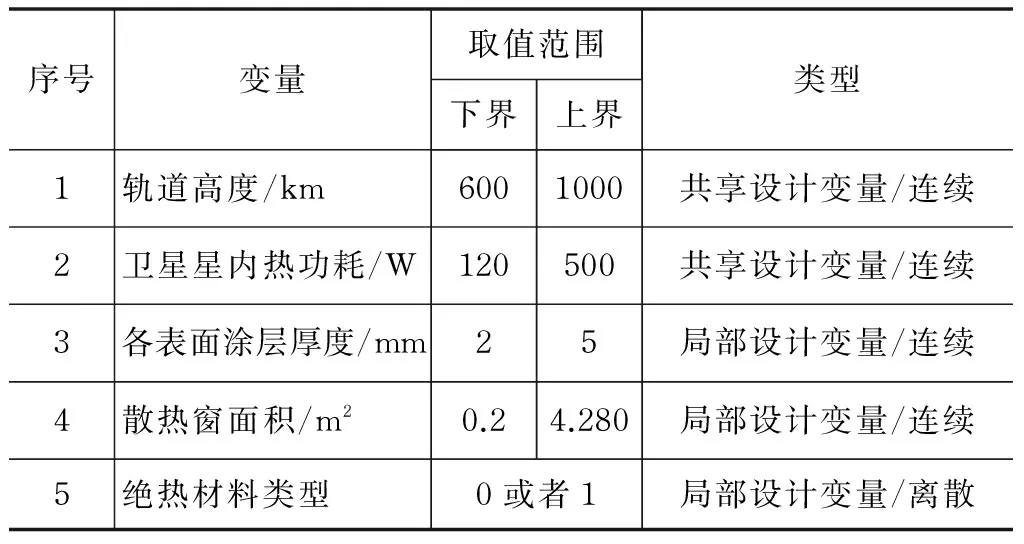
表6 热控分系统设计变量取值范围
g) 测控分系统优化模型
测控分系统优化模型如公式(10)所示:
find:xi={h,DR,f,Aan,t,Aan,r}
minmTTC,PTTC
(10)
s.t.mTTC≤135 kg
其中,卫星轨道高度h和载荷总数据率DR是共享设计变量;射频载波频率f、发射天线口面面积Aan,t和接收天线口面面积Aan,r是局部设计变量。优化目标是质量mTTC和功率PTTC最小,共享变量h和DR最接近系统级提议的目标值。设计变量取值范围如表7所示。
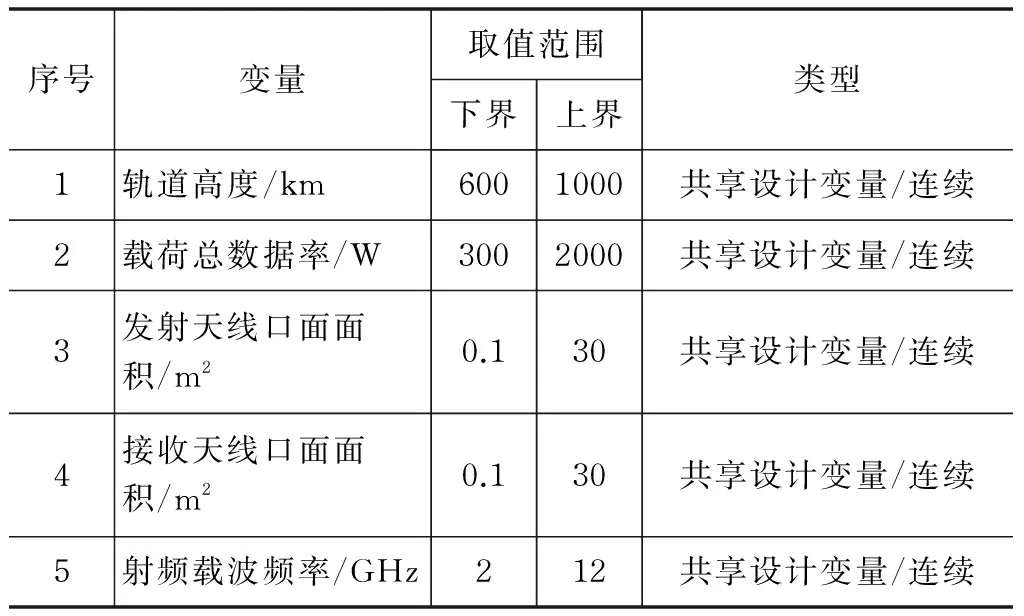
表7 测控分系统设计变量取值范围
3.2 优化结果分析
优化时在系统级和分系统级中均采用遗传算法(Genetic Algorithm GA)作为优化方法。本节给出分系统优化模块对优化过程的作用分析结果和两种方法的优化结果比较情况。
3.2.1 分系统优化模块对优化过程的作用
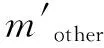
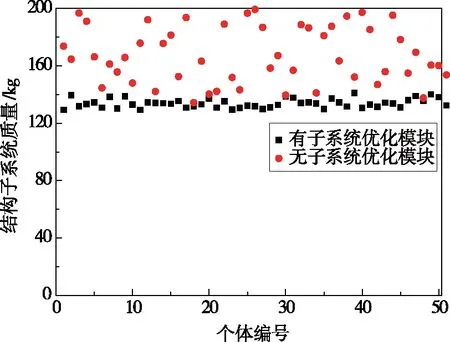
图3 分系统优化模块对结构分系统质量的优化作用Fig.3 The optimization function of subsystem optimization module on the mass of structure subsystem
由图3可见,经过结构分系统优化模块优化后的结构分系统质量均小于在满足条件下随机生成的结构分系统质量。表明对分系统进行优化设计,有利于分系统最优。
3.2.2 协同优化方法改进前后优化结果比较
表8给出改进前后优化结果中各分系统质量的比较情况。由表8可见,改进后的优化结果中除了电源分系统和结构分系统的质量略有增加外,其余5个分系统的质量均减小。最终卫星总质量也减小了大约4%,可见引入分系统自身优化可以得到更优解。

表8 优化结果中各分系统质量及卫星总质量的比较情况
4 结束语
本文通过在传统协同优化方法中引入分系统自身优化目标,提出了改进的协同优化方法。采用传统的和改进的协同优化方法对卫星总体优化模型进行优化研究,比较了两种方法的优化结果。结果表明:引入分系统自身优化目标的改进协同优化方法在优化过程中分系统的优化目标比不考虑分系统自身优化的传统协同优化方法更优;改进方法获得了比传统方法更优的优化结果。因此,证明了改进方法对卫星总体设计的有效性。
[1] Kroo I, Altus S, Braun R, et al. Multidisciplinary optimization methods for aircraft preliminary design [C]. The 5th AIAA/NASA/USAF/ISSMO Symposiumon Multidisciplinary Analysis and Optimization. Panama, 1994: 697-707.
[2] Huang, H., H. C. An, W. R. Wu, L. Y Zhang, B. B. Wu, and W. P. Li. Multidisciplinary design modeling and optimization for satellite with maneuver capability [J]. Structural and Multidisciplinary Optimization, 2014, 50:883-898.
[3] Braun, R. D., R. W. Powell, R. A. Lepsch, D. O. Stanley, and I. M. Kroo. Comparison of two multidisciplinary optimization strategies for launch-vehicle design [J]. Journal of Spacecraft and Rockets, 1995, 32 (3): 404-410.
[4] Jun, S., Y. H. Jeon, J. Rho, and D. Lee. 2006. Application of collaborative optimization using genetic algorithm and response surface method to an aircraft wing design [J]. Journal of Mechanical Science and Technology 20 (1): 133-146.
[5] Cao A. X., M. Zhao, W. Liu, and W. C. Cui. Application of multidisciplinary design optimization in the conceptual design of a submarine [J]. Journal Ship Mechanics, 2007, 11 (3): 373-382.
[6] 韩明红, 邓家褆. 协同优化算法的改进[J]. 机械工程学报, 2006, 42(11): 34-38.
[7] Ilan Kroo, Valerie Manning. Collaborative Optimization: Status and Directions [C]. The 8th AIAA/NASA/ISSMO Symposium on Multidisciplinary Analysis and Optimization, 6-8 September 2000, Long Beach CA. AIAA-2000-4721.
