神经网络在吸气式高超声速导弹突防弹道设计上的应用

魏黎明,李晓龙,赵 征,杜 厦,汪九州

(上海机电工程研究所，上海，201109)

0 引 言

导弹的巡航段不仅要将导弹的战斗部运送到指定位置，往往还需要有一定的突防能力。为增强导弹巡航段的突防能力，常用的方法是进行机动。

文献[1]针对高超声速飞行器巡航段的飞行，在等高等速的条件下，提出了一种能够满足飞行过程中多约束条件以及终端航向角约束的制导方法，推导得到了满足多约束条件的最优制导律，但未考虑纵向平面。文献[2]在只考虑水平面的侧向机动，纵向保持平飞的情况下，采用弹道仿真方法来求取超声速反舰导弹蛇形突防舰空导弹的突防概率，也未考虑纵向平面，且研究对象不是吸气式高超声速导弹。文献[3]针对一般的中远程导弹中制导段，提出了一种基于神经网络的最优中制导律，这种制导律通过离线学习，能够在线实时工作，与其他末制导律配合，可有效提高导弹拦截机动目标的性能，其研究对象不是吸气式高超声速导弹。文献[4] 采用针对固定目标、且能满足复合制导中制导要求的最优中制导律来提供神经网络的训练样本，以各时刻导弹及目标的位置坐标作为神经网络输入，经过计算输出相应的中制导指令，并通过仿真验证了基于神经网络的中制导律不仅能用于攻击固定目标及机动目标，同时能满足复合制导中末交班的各项要求。

由于吸气式高超声速导弹侧向机动能力较弱，因此在进行机动的过程中只考虑纵向机动，且吸气式高超声速飞行器发动机正常工作对攻角要求十分严格，攻角变化范围通常只有几度[5]。仿真表明，导弹在巡航飞行时其极限过载小于导弹所能承受最大过载，所以可以用极限过载进行机动来获得最大的机动能力。对吸气式超燃冲压发动机来说，存在着弹道飞行走廊[6]，即导弹工作动压窗口，导弹在纵向平面内进行机动时会因此受到限制。为解决上述问题，保证导弹在机动过程中不飞出动压窗口，利用BP神经网络通过导弹机动初始高度、马赫数以及质量预测导弹的最大纵向机动距离，使得在机动过程中导弹的动压可以维持在动压窗口内。

1 动压窗口约束条件

吸气式高超声速导弹的工作的动压窗口示意图如图1所示。动压窗口的上界和下界随着马赫数的增加不断地减小。

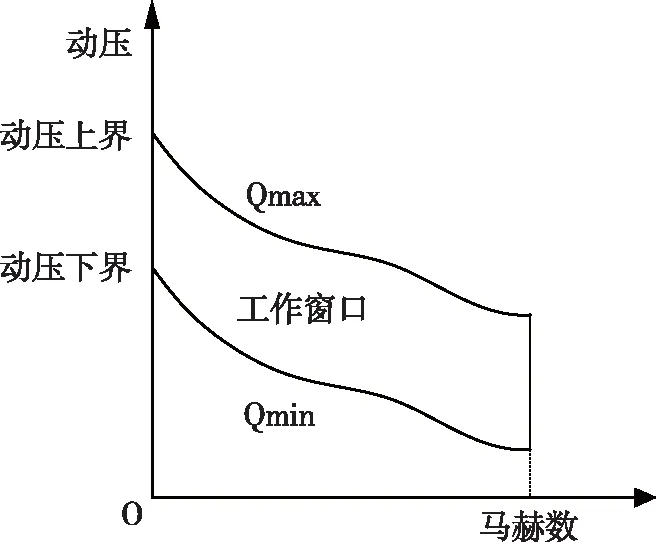
图1 导弹动压窗口Fig. 1 The dynamic pressure window of the missile

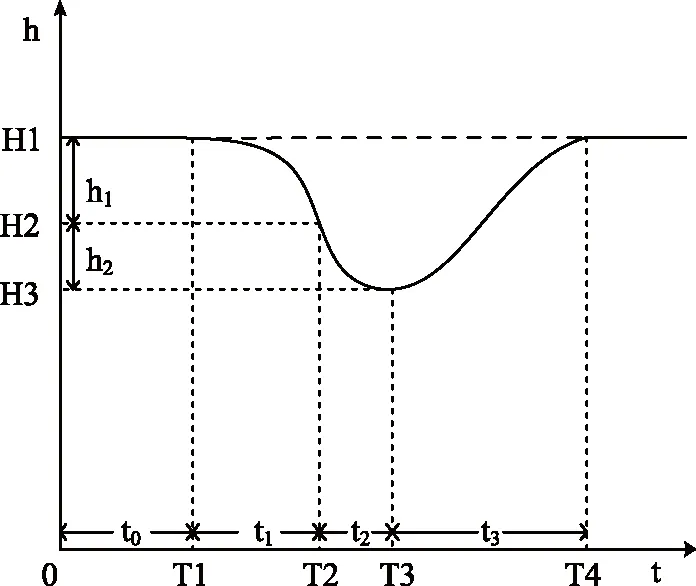
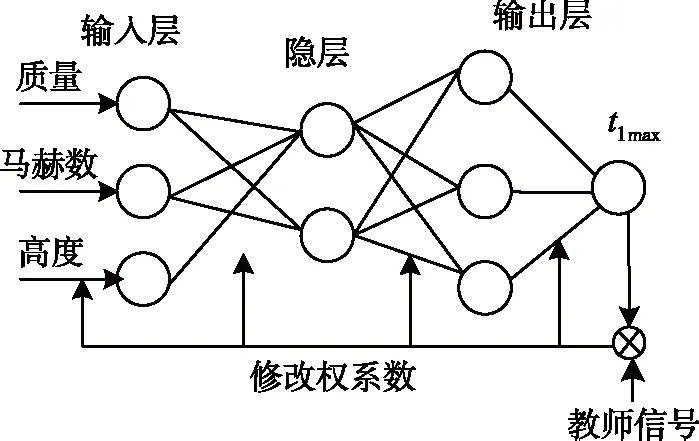
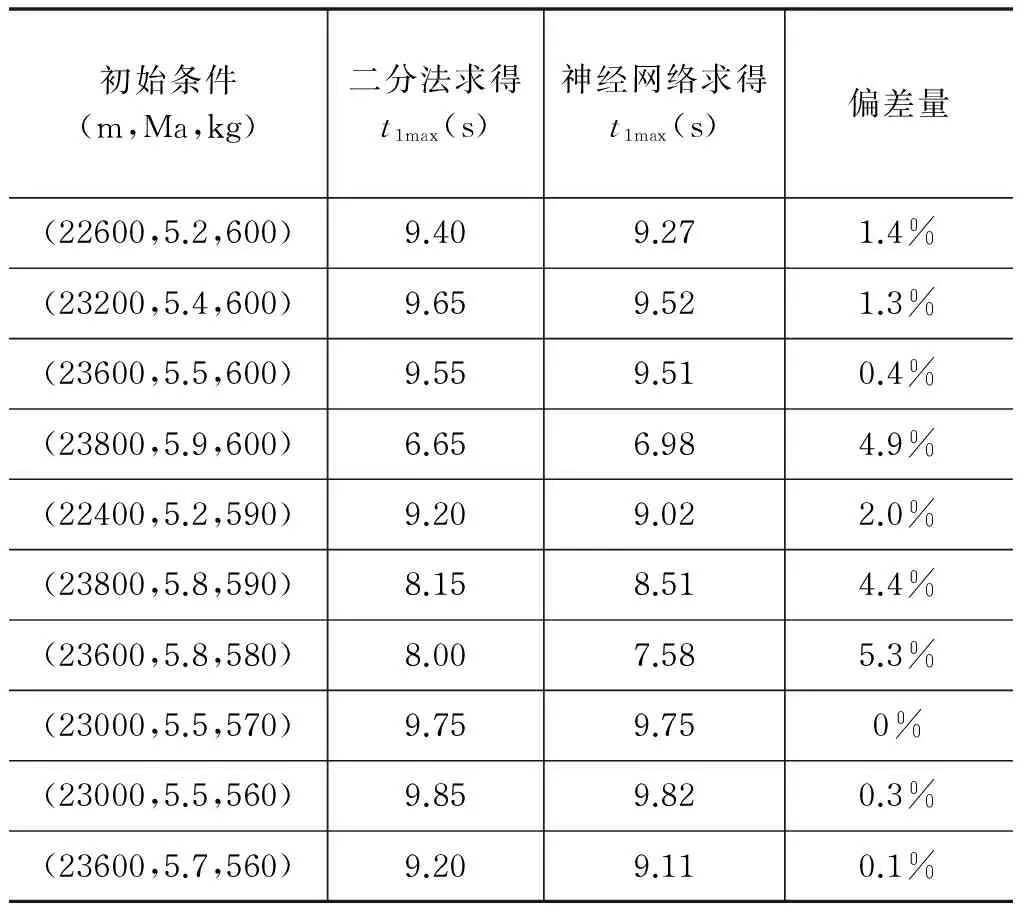
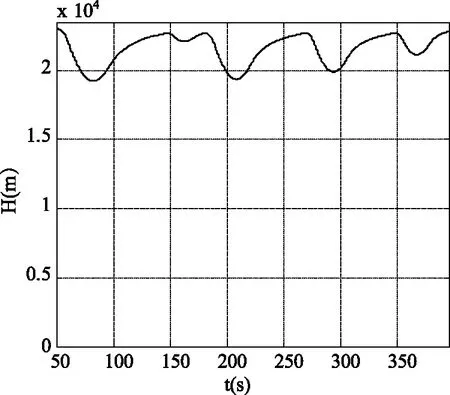
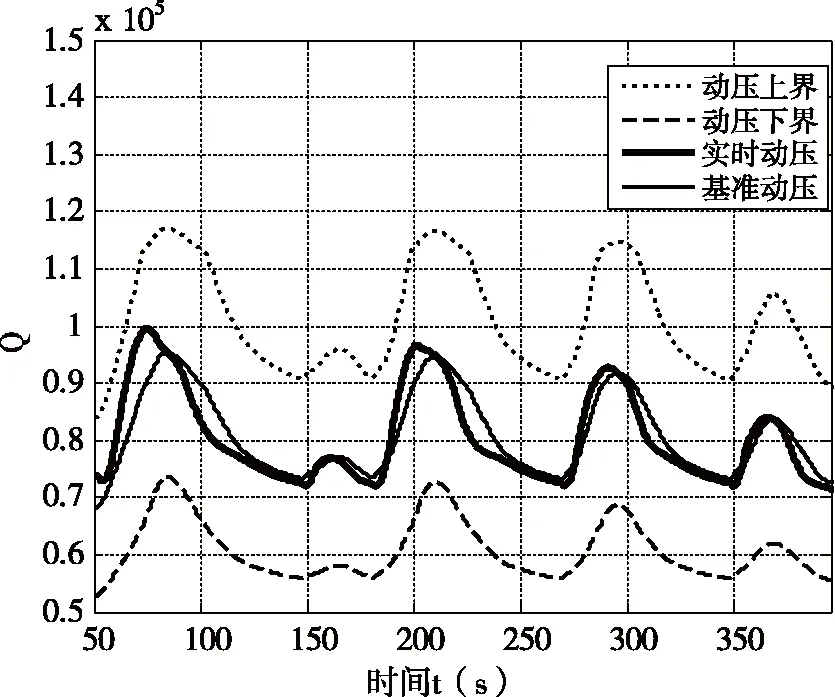
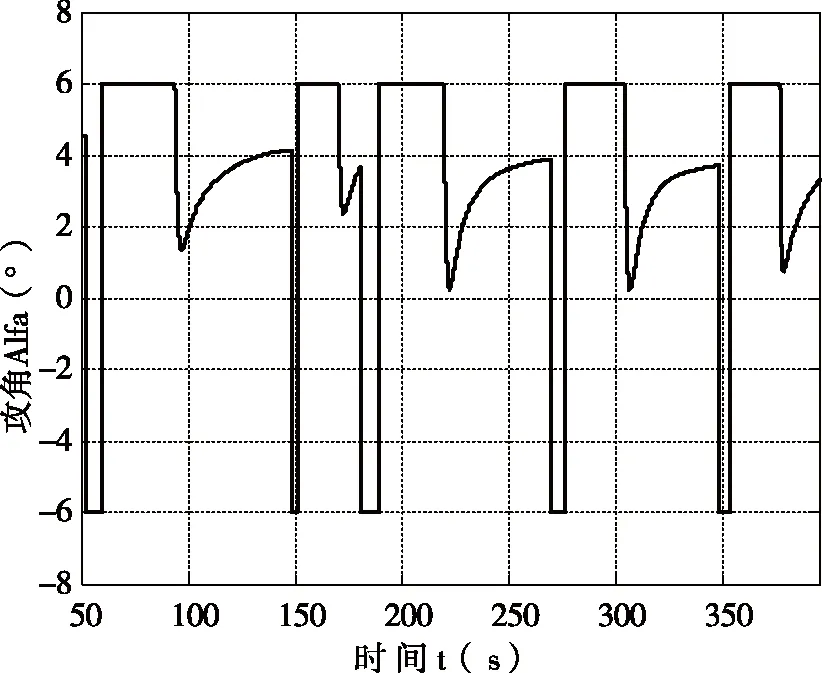
为研究方便，现假设吸气式超燃冲压发动机在某一瞬间的动压处于其工作动压窗口之间(即Qmax

2 基于BP神经网络的纵向机动时间预测

为了保证导弹在机动过程中不飞出动压窗口，需要知道导弹在动压窗口内的最大机动能力。利用BP神经网络通过导弹机动初始高度、马赫数以及质量可以很好地预测导弹的最大纵向机动能力。

2.1 纵向机动问题

现考虑导弹以极限过载进行的机动。

由于动压工作窗口的存在，导弹在采用极限过载进行机动一定时间后，必须回调弹道，使得导弹不飞出动压窗口。

以纵向平面内向下机动为例，机动示意图如图2所示。

图2 高度曲线Fig. 2 Height curve

导弹在T1时刻之前做巡航飞行，巡航高度为H1，在T1时刻接受机动指令，此时导弹的攻角为负的最大值，历时t1，在T2时刻开始回调弹道，即在T2时刻开始执行回调指令，将攻角拉到正的最大值，历时t2，直至时刻T3弹道倾角变为0，然后进行爬升指令，历时t3到时刻T4回到机动前的高度。

由于导弹利用极限过载进行机动时，机动时间t1的最大值t1max未知，t1max的值的大小与导弹机动初始马赫数、高度以及质量有关。为得到t1max与导弹机动初始马赫数、高度以及质量的关系，先通过大量仿真，得到不同机动初始马赫数、巡航高度对应的t1max值，然后经过BP神经网络的训练来找寻机动初始马赫数、巡航高度和t1max的关系。最后根据这个关系由任意机动初始马赫数和机动高度来预测机动时间t1max。

2.2 基于BP神经网络的纵向机动时间最大值预测

经过分析，导弹以极限过载进行向下机动时，其机动时间的最大值与机动初始状态下导弹的速度、高度、质量以及弹道倾角有关。弹道倾角取统一值0°，则导弹以极限过载进行向下机动时的机动时间的最大值t1max与机动初始状态下导弹的速度、高度以及质量有关。

现以导弹机动初始质量、马赫数、高度为输入，导弹以极限过载进行向下机动时的机动时间的最大值t1max为输出的BP神经网络模型如图3所示。

图3 BP神经网络模型Fig. 3 The model of the BP neural network

将导弹机动初始高度、马赫数、质量作为神经网络的输入，导弹以极限过载进行向下机动时的机动时间的最大值t1max作为神经网络的输出进行训练。

t1max的二分法仿真值与神经网络的输出值以及偏差值如表1所示。

表1 两种方法的输出值

由表1可以看出，通过神经网络训练得到的导弹以极限过载进行向下机动时的机动时间的最大值与二分法得到的导弹以极限过载进行向下机动时的机动时间的最大值偏差很小，基本满足预测要求。

3 动压约束的纵向机动突防方法

3.1 动压约束的纵向机动突防方法设计

根据第2章研究的内容，导弹某一时刻的质量、速度以及高度决定了导弹以极限过载进行机动时间的最大值t1max，因此，取机动时间为trandom，其中trandom为小于t1max的随机数。在一次机动中，trandom时间段攻角取负的最大值,t2时间段攻角取正的最大值，t3时间段为导弹爬升段。

3.2 仿真分析

仿真得到导弹高度随时间变化关系曲线、动压随时间变化曲线以及攻角随时间变化曲线如图4～图6所示。

图4 高度曲线Fig.4 Height curve

图5 动压随时间变化曲线Fig.5 Dynamic pressure varies with time

图6 攻角随时间变化关系Fig.6 Angle of attack varies with time

在机动过程中，导弹的动压一直处于动压窗口内，高度在某一范围内变化，变化高度3 772 m，导弹的攻角一直处于约束范围 (-6°～6°)之内。

4 结束语

通过BP神经网络方法，根据机动初始巡航高度、马赫数以及质量来预测导弹以极限过载进行机动的机动时间的最大值， 然后取导弹以极限过载进行机动的机动时间为随机值，只要保证其小于导弹以极限过载进行机动的机动时间的最大值，即可使导弹纵向进行随机机动，具有不可预测性，且在机动过程中不会飞出动压窗口。

[1] 万雨君，陈克俊，刘鲁华，等. 高超声速飞行器巡航段多约束制导方法[J]. 国防科技大学学报，2014，36(1): 11-16.

[2] 王永洁，陆铭华. 超声速反舰导弹蛇形机动突防舰空导弹建模仿真[J]. 现代防御技术，2008，36(6) : 57-61.

[3] Song E J, Tahk M J. Real-time neural-network midcourse gui-dance[J]. Control Engineering Practice, 2001, 9(9) : 1145-1154.

[4] 王建栋，罗喜霜，张天桥. 基于神经网络的中制导律[J]. 兵工学报，2003，24(3):430-432.

[5] Walton JT. Performance Sensitivity of Hypersonic Vehicles to Change Angle of Attack and Dynamic Pressure[C].AIAA Paper, 1989, 89-2463.

[6] Czysz, P. and Murthy, SNB. Energy management and vehicle synthesis[J]. Developments In High-Speed Vehicle Propulsion Systems, 1996,581-686.