Gumbel分布分位数的广义置信区间

喻 雪，范永辉

（天津师范大学数学科学学院，天津300387）

设 X1，X2，…，Xn是分布函数为 F（x）的独立同分布的随机变量序列，Mn=max{X1，X2，…，Xn}，设存在常数列{an＞0}和{bn}，使得x∈R，此极值分布有3种类型，其中Ⅰ型分布称为Gumbel分布，Gumbel分布函数的表达式为

其中：μ（-∞ ＜ μ＜+∞）为位置参数；σ（σ ＞0）为尺度参数.位置参数为μ、尺度参数为σ的Gumbel分布记作G（μ，σ），其对应的密度函数为

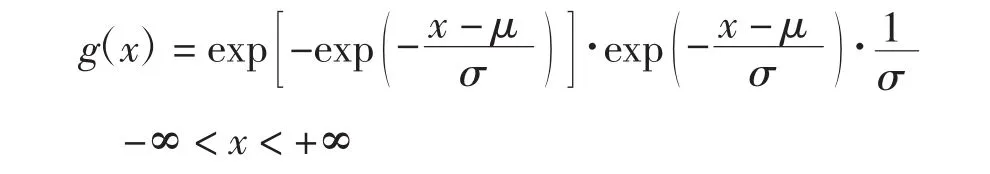
记 h（x）=exp[-exp（-x）]·exp（-x），则 Gumbel分布的密度函数可记为

Gumbel分布是极值分布的主要类型之一，极值分析的主要目的之一是估计分位数，其在水文、建筑、气象等领域有广泛的应用[1-3].对分布函数位置参数和尺度参数估计的优劣直接影响重现水平估计的准确性，因此对Gumbel分布参数的研究具有重大的理论意义和实用价值.

关于Gumbel分布的位置和尺度参数置信区间的确定，相关学者提出了很多方法.文献[4]利用样本分位数，构建极值分布参数的线性回归模型，得到了相关参数的渐近正态无偏估计，给出了相应的渐近置信区间.文献[5]基于样本分位数给出了构造置信区间的2个新枢轴量，推导出了枢轴量的概率密度函数表达式，在大样本场合讨论了总体参数的近似置信区间.文献[6]结合非线性回归模型和最小绝对偏差给出极值分布参数的一种估计方法.以上文献都是在大样本情况下考虑Gumbel分布中位置参数和尺度参数的置信区间，所用枢轴量的分布是当样本容量趋于无穷时的极限分布，但这些方法不一定适用于小样本情形，尤其典型的小样本置信区间在涉及讨厌参数统计问题时可能不可用，例如，2个指数分布的均值之间的差异，或两异方差的正态分布，典型的小样本推断不提供最佳的检验和置信区间.针对小样本情形，本文基于参数最小风险同变估计，利用广义枢轴量，构造了Gumbel分布分位数的广义置信区间.

定义[7]R=R（X，x，θ）是X、x、θ的函数，其中：θ =（θ1，θ2）为未知参数向量，θ1为感兴趣的参数，θ2为讨厌参数向量，若R满足以下条件，则称R为广义枢轴量（GPQ）.

（1）给定x，R的分布与未知参数无关.

（2）R的观测值Robs=R（x，x，θ）与讨厌参数无关.

设 R=R（X，x，θ）为参数 θ1的广义枢轴量，则θ1的等尾（1- α）100%的广义置信区间为[cθ1，α/2（x），cθ1，1-α/2（x）]，其中 cθ1，γ（x）满足

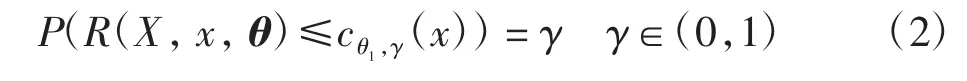
1 位置-尺度参数的最小风险同变估计

设随机变量ξ服从G（μ，σ），显然f（ξ）=aξ+b（a＞0，-∞ ＜ b ＜ +∞）服从 G（a μ+b，aσ）.μ、σ 的估计也应有类似的性质，即 X=（X1，X2，…，Xn）′是从总体 G（μ，σ）中抽取的样本分别为 μ 和 σ 的估计，若样本变为 aX+b1n，其中 1n=（1，…，1）′，则应满足

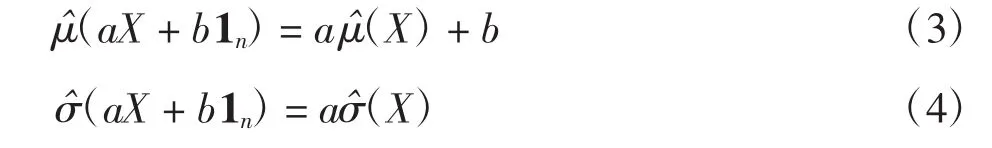
引理设 X=（X1，X2，…，Xn）′为来自 Gumbel分布G（μ，σ）的简单随机样本，则在二次误差损失函数下，位置参数μ的最小风险同变估计（MRE）为

类似文献[8]可得引理的证明.

2 Gumbel分布中参数的广义置信区间

首先构造广义枢轴量.设 X=（X1，X2，…，Xn）′是取自G（μ，σ）的简单随机样本，则在对参数μ和σ的估计为最小风险同变估计的基础上，分别构造位置参数μ和尺度参数σ的GPQ.位置参数μ的GPQ构造为

尺度参数σ的GPQ构造为

在求得μ和σ以及p分位数的GPQ后，根据式（2）可求得p分位数的广义置信区间.

令ciL和ciU分别为Ri分布的分位数和100×由式（2）可知μ、σ和p分位数的（1-α）广义置信区间分别为[c1L，c1U]、[c2L，c2U]和[c3L，c3U].虽然 Ri，i=1、2、3 的分布已知且与未知参数无关，但无法利用样本确定其分布，故广义置信区间需要通过计算机抽样模拟得到.

3 计算机模拟

本节通过计算机抽样模拟计算广义置信区间.首先给出算法流程，然后取不同的分位数，以及不同的小样本容量值，进行计算机模拟.

3.1 算法设计

取给定的μ、σ、n、p值，其中n表示样本容量.

对于 i=1，…，M，从 Gumbel分布 G（μ，σ）中抽取第 i个容量为 n 的样本，计算

对于 j=1，…，N，从 Gumbel分布 G（0，1）中抽取第 j个容量为 n 的样本 yj1，yj2，…，yjn，计算进而得出

{R31，R32，…，R3N}即为广义枢轴量 R3的一个容量为N的样本，分别用c1、c2表示该样本的分位数，总体分位数的广义置信区间即为[c1，c2]，假如c1≤μ≤c2，令 Ki=1，否则 Ki=0.计算得即为分位数的广义置信区间的实际置信水平（覆盖率）.

3.2 模拟结果

令 T=（1-p）-1，则 p=1-T-1，μ 分别取为 0、1，σ分别取为1、2、3.表1给出了样本容量n分别为5、10、15、20、35、40的情况下，T分别为 100、200、500的分位数0.95广义置信区间的实际置信水平（confidence level，CL）.

表1 T年重现水平的广义置信区间的置信水平Tab.1 Confidence levels of generalized confidence intervals of return period for T years

由表1数据可见，在样本容量较小的情况下，当μ、σ以及重现期T取不同的值时，p分位数广义置信区间的实际置信水平都与0.95非常接近，可见本文构造的广义枢轴量性能良好.

3.3 p分位数广义置信区间的另一种算法

文献[9]基于标准极值给出了一种GPQ的构造方式，下面利用本文方法和文献[9]方法分别计算Gumbel分布分位数广义置信区间的置信水平.由文献[9]，Gumbel分布 p分位数 μ-σ ln[-ln（p）]的 GPQ 为

不失一般性，这里只比较T=200时的分位数的0.95广义置信区间的实际置信水平以及平均区间长度（average interval length，AIL），μ分别取为 0、1，σ分别取为 1、2，样本容量分别取为 5、8、10、15、35、40，计算结果见表2.

表2 2种方法的广义置信区间的置信水平和平均区间长度（T=200）Tab.2 Confidence levels and average interval lengths of generalized confidence intervals of two methods（T=200）

由表2数据可见，在样本容量较小的情况下，总体来说，本文方法得到的置信水平略优于文献[9]，而平均区间长度则明显小于文献[9]的构造方式，说明本文的构造方法效果较好.

参考文献：

[1]罗纯，王筑娟.Gumbel分布参数估计在水位资料分析中应用[J].应用概率统计，2005，21（2）：169-175.LUO C，WANG Z J.The estimates of the parameters of Gumbel distribution and their application to the analysis of the water level data[J].Chinese Journal of Applied Probability and Statistics，2005，21（2）：169-175（in Chinese）.

[2]张新生，曹乃宁，王小完.Gumbel分布的油气管道的剩余寿命预测[J].中国安全科学学报，2015，25（9）：96-101.ZHANG X S，CAO N N，WANG X W.Residual life prediction of oil and gas pipeline based on Gumbel distribution[J].China Safety Science Journal，2015，25（9）：96-101（in Chinese）.

[3] 李颖，方伟华.热带气旋降水重现期估算研究[J].自然灾害学报，2014，23（6）：58-69.LI Y，FANG W H.Estimation on return period of tropical cyclone precipitation[J].Journal of Natural Disasters，2014，23（6）：58-69（in Chinese）.

[4]程维虎.利用样本分位数的极值分布的参数估计[J].北京工业大学学报，2002，28（3）：326-328.CHENG W H.Parameter estimation for extreme-value distribution based on the pi-th quantiles of samples[J].Journal of Beijing Polytechnic University，2002，28（3）：326-328（in Chinese）.

[5] 李永飞.极值分布参数基于不完全数据的区间估计[J].统计与决策，2015（433）：81-83.LI Y F.Interval estimation of parameters of extreme-value distribution based on in complete data[J].Statistics and Decision，2015（433）：81-83（in Chinese）.

[6] 吴香华，秦伟良，王新蕾，等.用最小绝对偏差方法（LAD）估计极值分布参数的探讨[J].气象科学，2006，26（3）：3260-3264.WU X H，QIN W L，WANG X L，et al.Regressive parameter-estimatingwithleast absolute deviation in extreme value distribution[J].Scientia Meteorologica Sinica，2006，26（3）：3260-3264（in Chinese）.

[7] TSUI K W，WEERAHANDI S.Generalized p-values in significance testing of hypotheses in the presence of nuisance parameters[J].Journal of the American Statistical Association，1999，84（406）：602-607.

[8] NKURUNZIZAS，CHENF.Generalizedconfidenceintervaland p-value in location and scale family[J].Sankhya B，2011，73（2）：218-240.

[9] 赵桂梅，崔玉杰.Weibull分布兴趣参数的广义置信区间[M].工程数学学报，2010，27（3）：567-570.ZHAO G M，CUI Y J.Generalized confidence intervals for interest parameters of the Weibull distribution[J].Chinese Journal of Engineering Mathematics，2010，27（3）：567-570（in Chines）.