利用地应力校正致密砂岩储层弹性参数方法
2018-05-07丁锐鹏胡元伟惠徐宁黄东安
丁锐鹏, 胡元伟, 惠徐宁, 黄东安, 杨 琦, 尹 帅
(1中国石油长庆油田分公司第十一采油厂 2中国石油新疆油田公司勘探开发研究院 3中国石油长庆油田分公司第一输油处 4西安石油大学地球科学与工程学院)
该文以川西地区三叠系致密砂岩储层为例,利用差应变实验及压裂法确定储层地应力大小,在考虑岩石热膨胀系数(β)基础上,提出了利用地应力校正致密砂岩储层弹性参数(杨氏模量及泊松比)的方法,同时与常规动静态参数转换方法进行了对比。研究结果对指导非常规致密储层地应力场模拟、压裂设计及井网优化等方面均具有一定参考价值。
一、 动静态参数转换关系
测试样品取自川西三叠系须家河组地层,为致密砂岩岩样。对样品进行了三轴力学及声学同步测试,测试仪器为MTS岩石物理测试系统。应力载荷误差<1%,应变量移动精度为0.000 1 mm。测试样品尺寸为25 mm×50 mm,饱和地层水,测试围压为32 MPa。所测试致密砂岩岩样的动静态弹性参数转换关系如图1所示,动态参数物理方程见式(1)、式(2)。从图1可以看出,无论是杨氏模量还是泊松比,测试数据均在1 ∶1等值线(虚线)以下,表明致密砂岩的弹性参数静态值均略小于动态值[1]。

图1 测试岩样动静态弹性参数转换关系
测试岩样的动静态杨氏模量间相关性较好,可靠性较高。但对于泊松比,由于致密砂岩自身存在较强的非均质性,因而动静态泊松比间转换关系相对较差。特别当测试岩样中存在一些裂缝(岩心尺度)时,会引起所测试的泊松比静态值明显高于其动态值(图1b),进而使两者相关性变差[2]。因此,实验测试中的动静态泊松比转换关系主要针对结构完整的测试岩样。对于含裂缝样品,其已发生应力卸载,因此应力要相对低一些,其泊松比要相对高一些[3]。
(1)
(2)
式中:ρ—岩石密度,g/cm3;
Vp和Vs—分别为纵波波速和横波波速,m/s;
E—杨氏模量,GPa;
ν—泊松比,无量纲。
测试岩样的静态杨氏模量及静态泊松比间也具有非常好的负相关性(图2)。这主要是由于,在地质埋藏过程中,随着岩石逐渐被压密,代表其刚度大小的杨氏模量逐渐增加,而泊松比逐渐降低[1-3]。这两者间具有非常好的负线性关系,相关系数高,表明可以利用泊松比对岩石杨氏模量进行定量表征,这两者均为静态值。
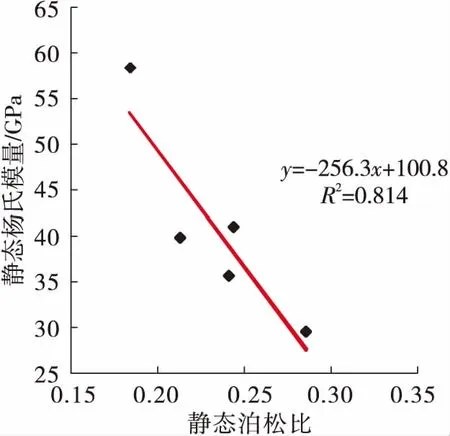
图2 测试岩样静态弹性参数间关系
二、地应力数据获取
微型压裂施工由于消除了邻层及岩性变化等因素的影响,应用效果最好。差应变分析(DSA)也能获取可靠的地应力数据,该项测试由差应变测试分析系统仪完成。通过对岩心加压,进行不同方向的应变分析,得到最大与最小主应力在空间的方向及取值。该文采用压裂法和差应变实验测试获取研究区6口井部分层段的地应力数据,共计8组,结果见表1。
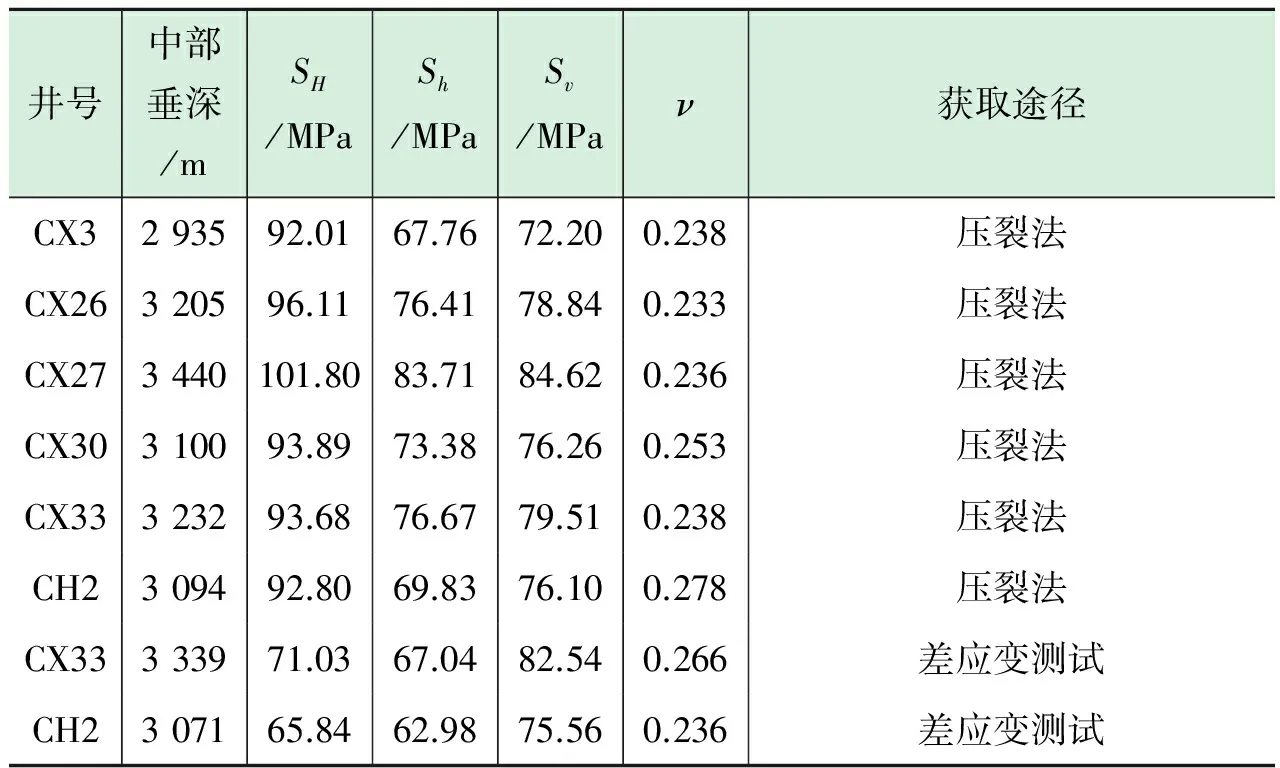
表1 不同测试方法获取的地应力结果表
三、利用地应力校正弹性参数方法
地壳表层沉积岩体具有一定温压梯度,随着埋深的增加,地层应力和温度均逐渐升高。对于埋深一定的沉积岩体,其水平方向主应力受岩石弹性力学参数及温度梯度的综合控制和影响。此时,岩石水平方向最小主应力(Sh)可由式(3)表示[4]。
(3)
式中:β—热膨胀系数,不同类型岩石具有不同的β值,可通过文献[5-7]查值获取(表2);
G—地温梯度,℃/m;
H—地层埋深,m;
E—杨氏模量,此处其单位为MPa。

表2 不同岩性岩石热膨胀系数β取值表
由式(3)可以看出,地层Sh受岩石弹性力学参数(如E和ν)及温度梯度参数(如β和G)的共同控制。单从式(3)来看,ν和E均对地层Sh均起正向作用,即地层Sh随着ν值或E值的增加而增加。但对于真实地质体而言,ν值的增加会引起E值的降低。因此,实际地层Sh的变化受ν及E的耦合作用影响[6]。图2中显示,所研究致密砂岩的ν和E具有非常好的负相关性,该砂岩的ν值主要分布在0.15~0.35之间。根据图2所示转换关系,利用杨氏模量表征泊松比,代入式(3),可得:
(4)
式(4)同时考虑了ν及E的变化对地层Sh的影响。对于研究区而言,目地层的G值可取0.025℃/m,H取平均值3 000 m,Sv的应力梯度取0.025 MPa/m。对于β值,根据表2可知,不同类型岩石具有不同的β值,β值的大小与岩石内部矿物组分及其排列方式等因素有关,砂岩的β值主要分布在(5~12)×10-6/℃[5-7]。因此,通过在合理取值范围内对β赋不同值,可建立研究区目的层Sv与泊松比(0.15<ν<0.35)间的关系图版,见图3。
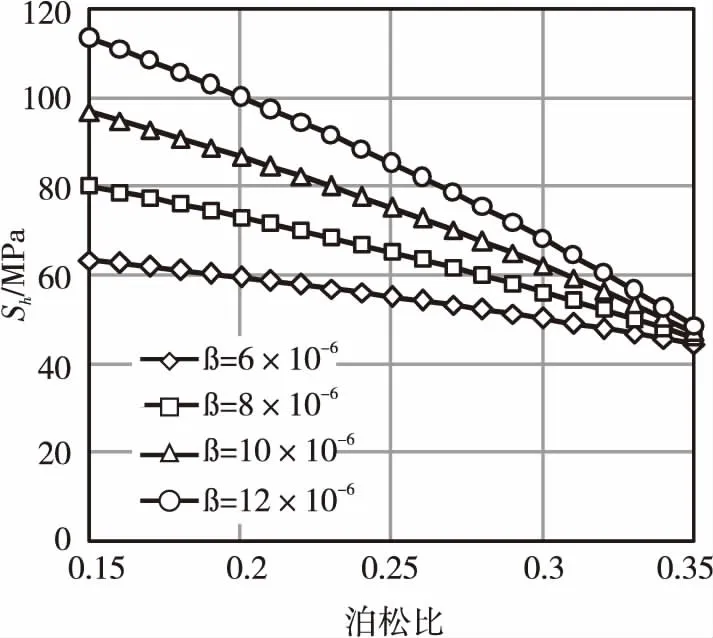
图3 研究区目的层Sv与泊松比间关系图版
由图3可以看出,对于研究区目的层而言,随着地层ν值的增加,Sv逐渐发生降低。Sv的降低幅度与岩石β值有关,当β值较小时(如β=6×10-6/℃),地层Sv的降低幅度较缓;随着β值的逐步增加,地层Sv的降低幅度逐渐变陡。当ν值较小时(如ν=0.15),岩石具有较大的刚度,此时β值对地层Sv的影响程度较大;随着ν值的逐渐增加,如当ν=0.35时,β值对地层Sv的影响已经不再显著。整体来看,β值越大,所预测的地层Sv值越大。由于研究区目的层致密砂岩的ν值主要分布在0.2~0.3的范围内,因此,β值对Sv的影响不容忽视。
将表2中的测试数据代入式(4),对式(4)的可靠性进行验证。利用式(4)的Sh预测结果与实测值间的对比关系见图4,其分别考虑了不同的β取值。可以很明显看出,当β值取9×10-6/℃时,Sh预测结果与实测值间极为相符。因此,对于所研究致密砂岩储层,当式(4)中取β=9×10-6/℃时,该计算模型最为可靠。
式(4)中隐含了研究区目的层E的信息,因此综合考虑了各弹性参数及温度参数对Sh的影响。同时,当β取9×10-6/℃时,该计算模型最为可靠。在此评价基础上,将Sh设定为自变量,ν设定为因变量,即利用Sh表征ν,可得:
(5)
上述式(5)即为本文所提出的利用地应力对弹性参数进行校正的一般表达式。

图4 Sh预测结果与实测值间对比图
四、测井分析实例及讨论
上述式(5)可用于地应力测井评价结果的检验。对于研究区目的层,β取9×10-6/℃,G取0.025℃/m。将测井解释的地层Sh、Sv及H带入式(5),可求取相应深度岩石ν值。利用图2所示拟合方程可获得相应E值。将该E值及ν值与根据常规动静态校正转换方法获取的E值及ν值进行对比,从而对不同方法所确定的地层岩石弹性参数可靠性进行判定。
图5所示为研究区CX26井目的层地应力及弹性参数测井评价结果,该地层埋深分布在3 150~3 300 m范围,岩性整体以致密砂岩为主,局部夹具有较高泥质含量(Vsh)的薄层泥页岩,地应力状态为Sh

图5 CX26井地应力及弹性参数测井评价成果图
对于E而言,对于泥质含量较低的砂岩层段,两种方法解释结果极为一致;而对于泥质含量含量较高的地层段,本文方法所解释的E值略低于常规方法解释结果。对于致密砂岩储层来说,泥质组分对岩石E的影响极为显著。前人研究表明,随着泥质含量的增加,岩石E及声学参数均会发生明显降低[9]。两种方法对ν的评价结果具有较大的差异性,而对E评价结果的差异性较小,这与致密砂岩储层自身的强非均质性及各向异性有关。这种差异性对ν来说要远远大于E,说明利用常规方法所建立的致密砂岩储层泊松比动静态值转换关系可靠性较低;而杨氏模量的动静态值转换关系基本可靠。利用本文所提出的方法可以对致密砂岩储层弹性参数进行校正,校正后的弹性参数变化规律与地应力间相符性变好。因此,该技术方法具有一定推广应用价值。
五、结论
(1)该文以川西地区三叠系致密砂岩储层为例,利用差应变实验及压裂法确定储层地应力大小,在考虑岩石热膨胀系数(β)基础上,提出了利用地应力校正致密砂岩弹性参数(杨氏模量及泊松比)的方法。
(2)利用常规方法所建立的致密砂岩储层泊松比动静态值转换关系可靠性较低;而杨氏模量的动静态值转换关系基本可靠。
(3)β对地应力的影响不容忽视,目的层致密砂岩β值取9×10-6/℃时,所提出的预测模型可靠。通过本文方法对弹性参数进行校正后,弹性参数变化规律与地应力间具有更好的相符性。该方法相比常规方法而言,解释结果更为合理。
[1]Pickett.Acoustic character logs and their applications in formation evaluation[J].SPE452,1963,659-667.
[2]Kate Hadley.Vp/Vs anomalies in dilatants rock samples[J]. Pure and Applied Geophysics,1975,113:1-21.
[3]Marek Grad,Urmas Luosto.Fracturing of the crystalline uppermost crust beneath the SVEKA profile in central finland[J]. Geophysica Physics,1992,28(1-2):53-66.
[4]Bonner B P.Vp/Vs in saturated granodiorite loaded to failure[J]. Pure and Applied Geophysics,1975,113:25~28.
[5]Sheorey P R. A theory for in situ stresses in isotropic and transversely isotropic rock[J].International Journal of Rock Mechanics and Mining Sciences,1994,31:23-24.
[6]Haas C J. Static stress-strain relationships. In: Touloukian YS, Ho CY, editions. Physical properties of rocks and minerals. Ⅱ—2[M]. New York,McGraw Hill, 1981:410-482.
[7]Schafer K. In situ strain measurements in Libya[J]. Rock Mechanics,1980,9(Suppl): 49-60.
[8]Van K D W. Coal[M].Amsterdam, Elsevier,1961:514-516.
[9]Castagna,Batzle,Eastwood.Relationships between com-pressional-wave and shear-wave velocities in clastic silicate rocks[J]. Geophysics,50(4).571-581.
