基于压缩感知的DRM信道估计

聂阳

(中国传媒大学 广播电视数字化教育部工程研究中心，北京 100024)

1 引言

模拟调幅广播具备范围覆盖广泛，便于移动接收、成本接收低等优点，长期以来被认为是区域化广播覆盖的有效手段之一，但也存在业务类型单一和信号易受干扰等缺点。随着数字广播技术的不断涌现，数字化调幅广播的需求也特别迫切[1-2]。DRM标准[3]是全球开放性的、非专利性的、中短波调幅广播(30M以下)的数字广播标准，将功能单一的音频信息拓展为文字、图像和视频等多种媒体信息，为模拟调幅广播的数字化创造了一个多元化的优质平台。

DRM信道是频谱受限的时变多径信道，为了克服信道多径衰落并提高频谱资源利用率，DRM标准采用OFDM技术提高频带利用率，抵抗多径衰落。对于OFDM系统，接收端的相干解调和信道均衡均需要获得准确的信道信息，信道估计技术便在其中发挥着非常重要的作用[4-5]。

随着研究的不断深入，许多实际的无线信道在时域上具有很强的稀疏性，即信道冲激响应中只有少数明显的多径分量，其余幅度几乎为零[6-8]。在信道估计领域，Bajwa 等指出常见的无线多径信道普遍具有稀疏特性，可以将信道估计转化为压缩感知(Compressive Sensing/Compressed Sensing，CS)的稀疏信号重构问题[9]。CS理论认为，如果信号是可稀疏的，那么就可以通过感知矩阵将高维信号转换为低维信号，然后求解l0或l1范数优化问题，少量的低维信号被用来重建原始信号[10-12]。CS核心的问题是稀疏信号的感知与恢复，而信道估计的过程恰恰是稀疏信道冲激响应的感知与恢复，所以利用DRM信道固有的稀疏性质，将信道估计问题转化为信号的稀疏重构，以较少的导频获得精确的估计结果。

2 信道模型

DRM的信道模型适用于长、中、短三个波段的广播无线传输信道。由于电磁波在电离层和地球表面的传输机制，使得发送信号通过多种延时从不同的传播路径到达接收端。DRM信道是时变多径信道，为了描述这一信道特性，采用可变参数的广义平稳非相关散射模型来描述：

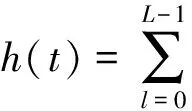
(1)

上式中ρl是第l条的路径衰减因子，Δl是第l条的路径延迟，cl(t)是时变抽头权重。cl(t)是均值为零的复平稳随机过程，相位满足均匀分布，幅值服从瑞利分布。

Y=XH+W=XFh+W

(2)

其中，X=diag(X1，X2，…，XN)是N×N对角矩阵，H是信道频域响应采样值，W是频域内高斯白噪声，F是N×N的标准傅里叶矩阵的前L列：

(3)

利用选择矩阵S从N个子载波中选出P个导频信号，则接收端的导频信号表示为：

YP×1=XP×PFP×LhL×1+WP×1=AP×LhL×1+WP×1

(4)

上式中YP×1、XP×P、FP×L和WP×1都是已知信号，可以通过一定的算法得到hL×1，则频域响应值H可由下式得出

HN×1=WN×LhL×1

(5)

DRM的信道冲击响应hL×1中只有少数幅值是非零值，因此该信道是稀疏信道，故(4)式中的hL×1是典型的稀疏信号重构问题，hL×1的求解完全可以采用CS的重构算法完成。

3 信号重构与仿真结果分析

基于CS的信道估计充分利用了信道本身的稀疏特征，用较少的导频信号实现信道估计，从而提升系统的传输效率。实验仿真的重构算法采用OMP(Orthogonal Matching Pursuit)算法[13]，并分析导频的插入方式和数量对重构性能的影响，估计的性能指标采用均方误差和系统的误比特率。系统仿真是在理想同步且无信道编码情况下进行的，鲁棒模式采用B模式，选择典型的短波信道(信道3)[3]。

3.1 导频图案对OMP信道重构算法的影响

在使用OMP算法完成信道估计时，选取三种导频图案排列的模式为：连续、均匀、随机。如图1所示，“连续模式”是指导频连续排列在子载波上；“均匀模式”是指导频等间隔的平均分布在子载波上；“随机模式”是指导频随机地分布在子载波上。

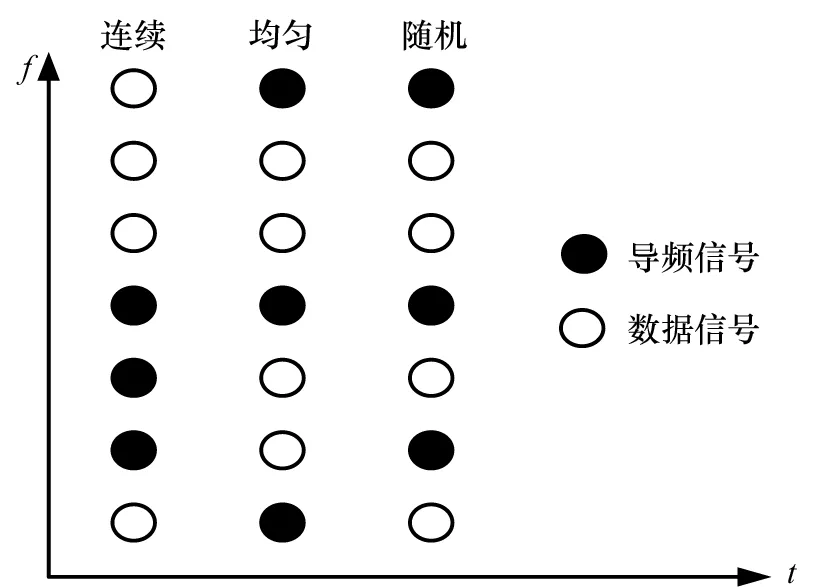
图1 三种导频的排列方式

从图2和图3的仿真结果可以看出，采用连续排列方式的导频图案，OMP 算法的信道估计性能最差，均匀排列方式的导频图案次之，随机排列方式的导频图案性能最优。其原因是导频的图案直接决定了感知矩阵A的形式，感知矩阵越随机，对信道稀疏位置的估计越准确，从而提高了信号重构的性能。

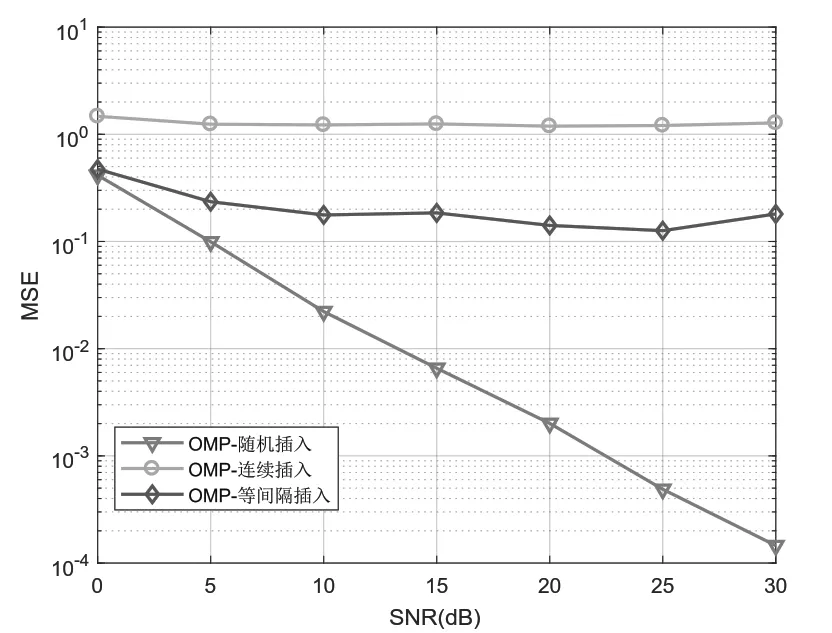
图2 OMP算法不同导频排列的MSE对比

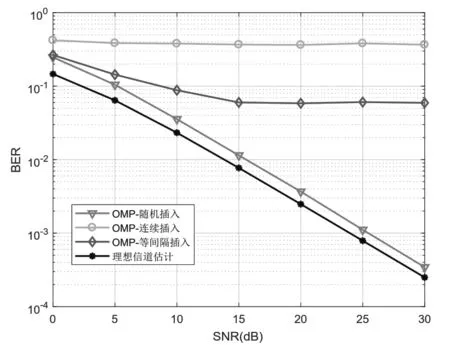
图3 OMP算法不同导频排列的BER对比

3.2 OMP与LS 的信道估计性能比较

通过前面的仿真发现OMP算法在导频随机排列时估计性能最佳，如果等间隔或连续放置导频，则MSE非常大。为了合理比较不同算法的信道估计性能，本节将用于OMP算法的导频随机排列，而LS算法的导频均匀排列。从图4的MSE曲线可以看出，导频数为26 和43的 LS 算法的系统MSE 均高于OMP算法。当信噪比小于5 dB时，OMP算法的优势并不明显，但随着信噪比的增加，OMP的重构性能变得越来越好；当信噪比是30dB时，LS算法的MSE明显劣于OMP算法。从图5的BER曲线可以看出，导频P=43的LS算法的信道估计性能，若换成OMP算法，则仅仅需要26个导频。导频占子载波的百分比不仅从16.8%降到10.1%，而且重构的性能也优于LS算法。

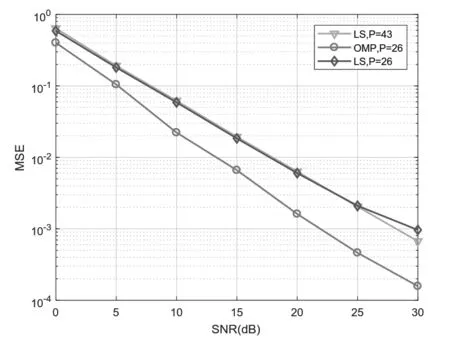
图4 OMP与LS信道估计的MSE对比

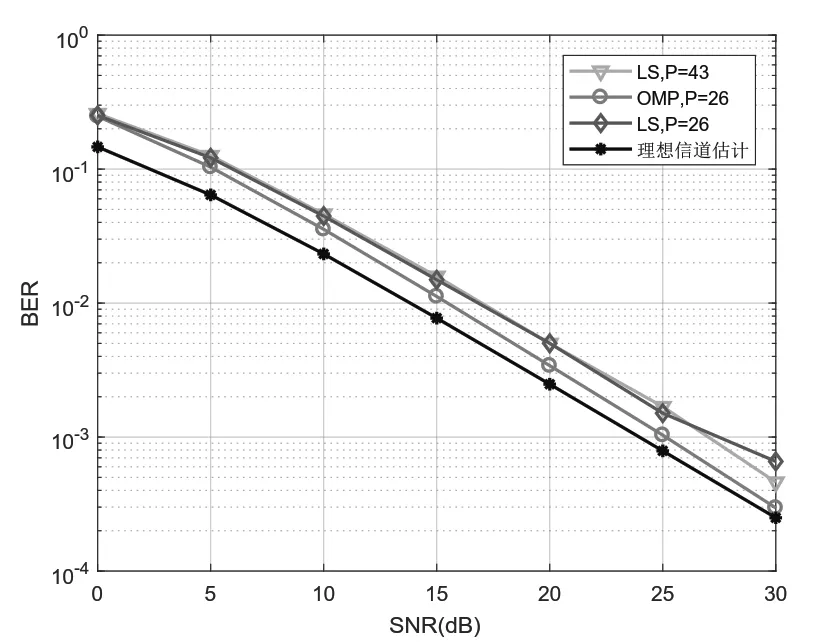
图5 OMP与LS信道估计的BER对比

3.3 导频数量对OMP信道重构的影响

在基于CS的信道估计中，导频的数目对应与OMP算法中的测量值个数，本次实验的主要目的是研究导频数目对OMP信道重构算法性能的影响。图6是随机排列模式下OMP算法不同导频数对应的MSE。从仿真结果可以看出，随着导频数目的增加，基于OMP算法的信道重构性能越来越好，但是当导频数大于26后，信道估计改善的效果不是很明显。图7是不同导频数目对应的BER比较，从图中可以看出，P=26、P=32和P=43时BER 曲线几乎重叠，而且估计的效果已接近理想信道估计。因此，继续增加导频数目的意义不大，反而会降低系统的频谱效率，综合考虑系统传输的有效性和可靠性，建议导频的数目应为稀疏度的6倍。

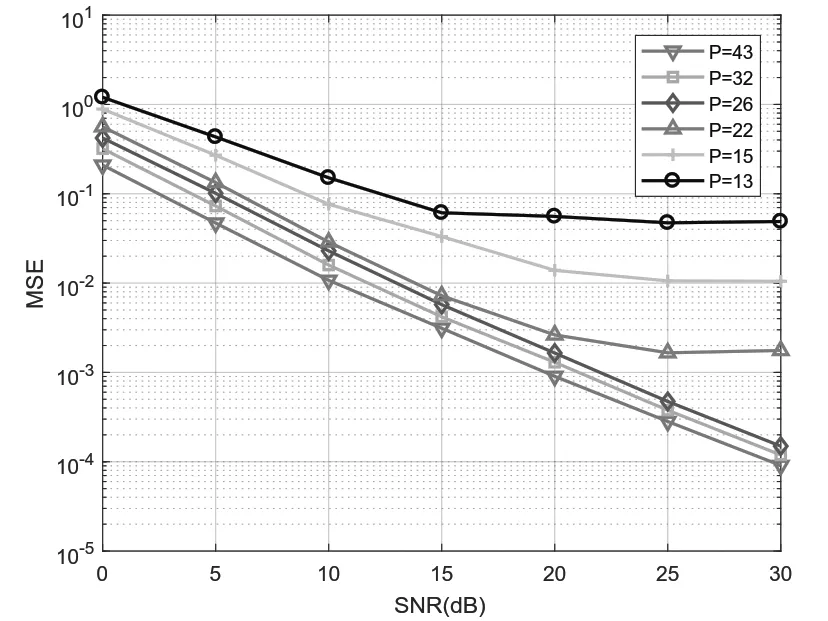
图6 OMP不同导频数目的MSE对比

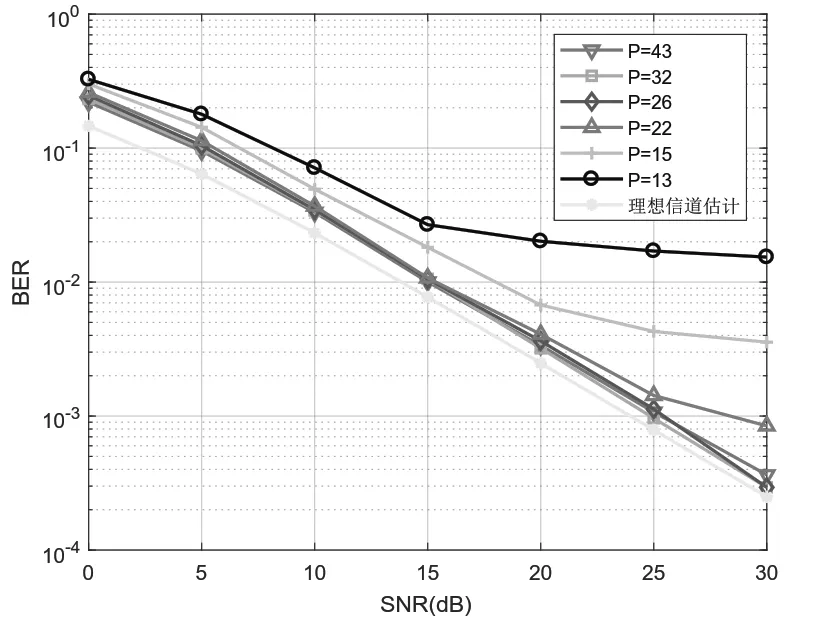
图7 OMP不同导频数目的BER对比

4 结论

针对DRM标准，本文以短波信道为例建立了基于CS理论的稀疏信道模型，分析了不同导频的插入方式和数量对重构性能的影响。与传统的LS信道估计比较而言，基于CS的信道估计不仅能够减少导频开销，而且可以提升估计的效果。因此，基于CS的信道估计是提高DRM系统信道估计性能的一种非常有效和实用的方法。

[1]徐伟掌，吕锐，杨占昕，卢起斌.传统 AM 发射机的 DRM 改造[J].中国传媒大学学报(自然科学版)，2005，12(2)：1-3.

[2]李江，吕锐，杨占昕.数字调幅广播(DRM)技术与应用研究[J].中国传媒大学学报(自然科学版)，2008，15(2)：1-5.

[3]ETSI ES 201 980 V2.3.1，Digital Radio Mondiale(DRM)System Specification，2008-02[Z].

[4]张继东，郑宝玉.基于导频的 OFDM 信道估计及其研究进展[J].通信学报，2003，24(11)：116-124.

[5]Liu Y，Tan Z，Hu H，et al.Channel estimation for OFDM[J].IEEE Communications Surveys & Tutorials，2014，16(4)：1891-1908.

[6]Muquet B，De Courville M，Duhamel P.Subspace-based blind and semi-blind channel estimation for OFDM systems [J].IEEE Transactions on signal processing，2002，50(7)：1699-1712.

[7]Negi R，Cioffi J.Pilot tone selection for channel estimation in a mobile OFDM system [J].IEEE Transactions on Consumer Electronics，1998，44(3)：1122-1128.

[8]Li Y.Pilot-symbol-aided channel estimation for OFDM in wireless systems [J].IEEE transactions on vehicular technology，2000，49(4)：1207-1215.

[9]Bajwa W U，Haupt J，Sayeed A M，et al.Compressed channel sensing：A new approach to estimating sparse multipath channels [J].Proceedings of the IEEE，2010，98(6)：1058-1076.

[10]Donoho D L.Compressed sensing [J].IEEE Transactions on information theory，2006，52(4)：1289-1306.

[11]Baraniuk R G.Compressive sensing [J].IEEE signal processing magazine，2007，24(4)：118-121.

[12]Candès E J，Wakin M B.An introduction to compressive sampling [J].IEEE signal processing magazine，2008，25(2)：21-30.

[13]Tropp J A，Gilbert A C.Signal recovery from random measurements via orthogonal matching pursuit [J].IEEE Transactions on information theory，2007，53(12)：4655-4666.