机械固定结合面动态特性的试验与研究*
2018-05-05周振财王天雷陈惠添
周振财,王天雷,王 柱,赵 挺,陈惠添
0 前言
机械产品是由多个零件或部件通过各种结合方式组装而成,因此整机中存在大量结合面。结合面将对其加工性能产生很大的影响;在刚度方面,结合部对整机的影响占到60%以上;在阻尼方面,结合部对整机的影响占到90%以上,结合面的动态特性的研究是整体分析需要解决的关键技术之一[1]。
从运动来看,结合面可以分为三类,即固定结合面、半固定结合面和运动结合面。影响结合面动态特性的因素很多,多为非线性,加之使用工况的多样化,各种因素相互交错影响,使问题变得更复杂。实际研究中,主要考虑的影响因素有:①结合面的材质;②结合面的加工方法;③结合面的加工质量;④结合面的介质状况;⑤结合面的法向压力;⑥结合面上动载荷的性质(如法向力、切向力、扭矩、弯矩)和大小;⑦结合面间的相对位移性质(法向位移、切向位移和转角等);⑧大小和相位差(与结合面上的动载荷之间的相位差);⑨振动频率;⑩结合面的功能和结合面结构类型和尺寸大小等。
影响因素可分基本影响因素和非基本影响因素[2-3],其中基本影响因素是反映结合面自身基本特性的影响因素;而非基本影响因素则是与结构设计有关,见表1。
本文采用正交试验法,研究几个因素对螺栓联接的固定结合面动态特性的影响,为研究其他结合面动态特性,以及数控机床的设计提供参考。
1 研究方法及评价指标
1.1 研究方法
目前,对机械结构或结构动态性能的研究主要有三种基本方法[4]:1)有限元理论建模及其分析方法;2)实验建模及分析方法;3)两者相结合的方法。本文采用第三种方法,试验研究流程见图2,即,设计正交试验,分析三因素对结合部动柔度的影响,动柔度值由实验测取,并用有限元模型进行验证,确认后进行极差分析计算。
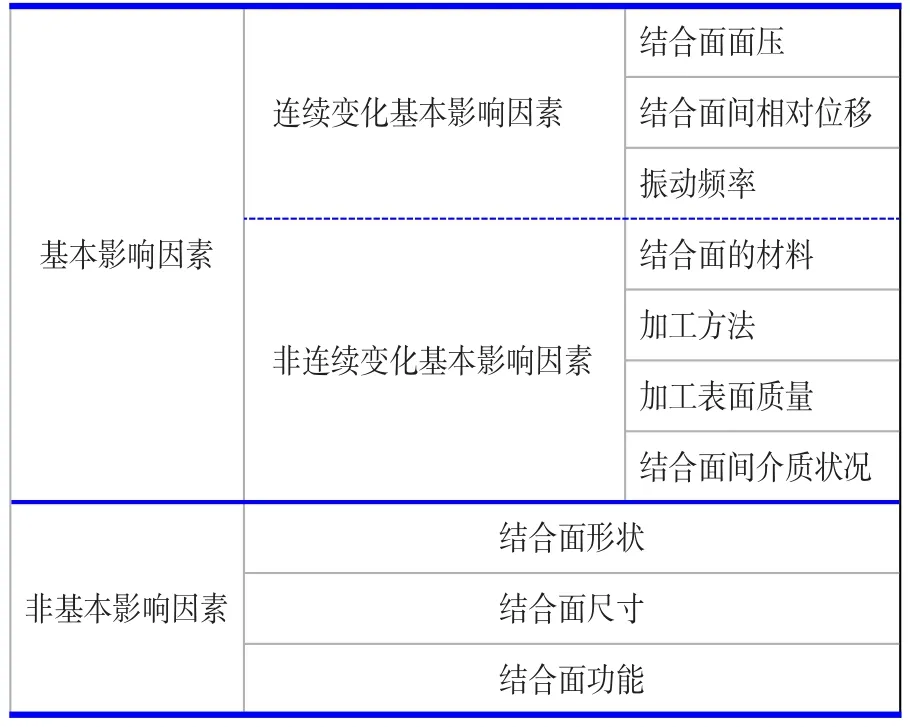
表1 结合面动态特性影响因素的分类
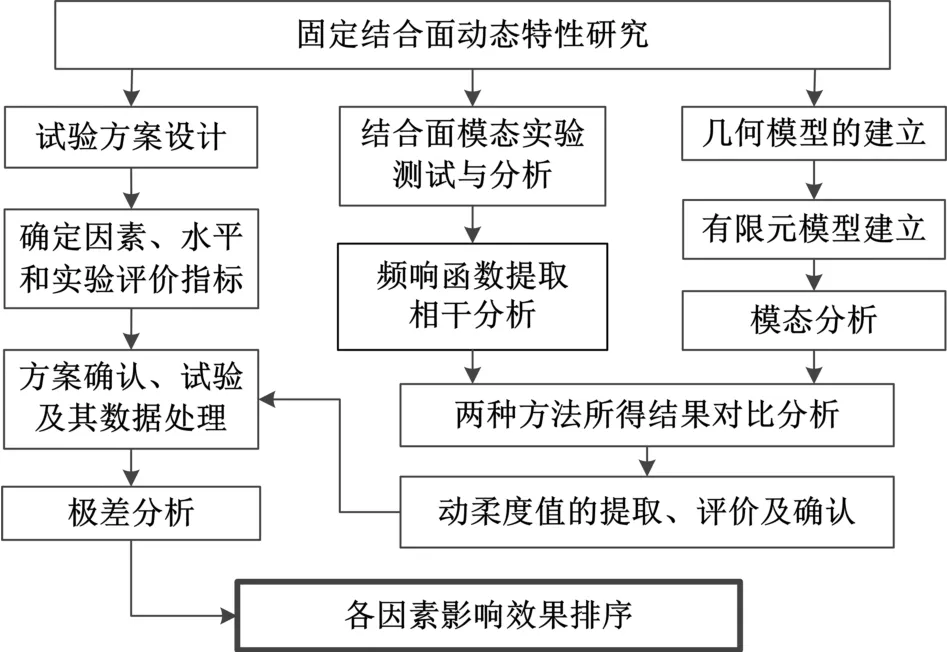
图1 固定结合面动态特性试验研究流程
1.1 动态特性评价指标
本文选择结合面影响因素分别为螺栓个数、螺栓预紧力矩和结合面的介质状况,确定动柔度值作为评价指标。动柔度与动刚度是倒数关系,动刚度是指抵抗外界动态力的能力,其数值等于产生单位振幅时所需要的动态力[5]。当系统产生共振时,动刚度最低,在频响函数曲线图上表现出来的则为动柔度值最大。实验时,通过改变上述三个影响因素的水平,构建不同的组合,测取对应的动柔度值。
2 动态试验与分析
2.1 实验装置
模态实验装置如图2所示,采用单输入/单输出识别法(SISO),实验时将螺栓联接的试件用弹性橡胶绳悬挂在支架,用4通道动态频谱分析仪,在FFT模块下对试验试件使用锤击法进行模态试验。试验装置主要包括:PCB公司三轴加速度传感器和冲击锤、美国Benstone公司4通道动态频谱分析仪IMPAQ Elite以及弹性橡胶绳、悬吊支架、数据传输线等,图3为测试现场。
试件材料为两块尺寸300 mm×100 mm×20 mm的矩形HT250铸铁板,可用多个M8螺栓联接,见图2、图3,结合面尺寸为300 mm×100 mm,接触表面均为精铣加工,粗糙度值为Ra1.6。
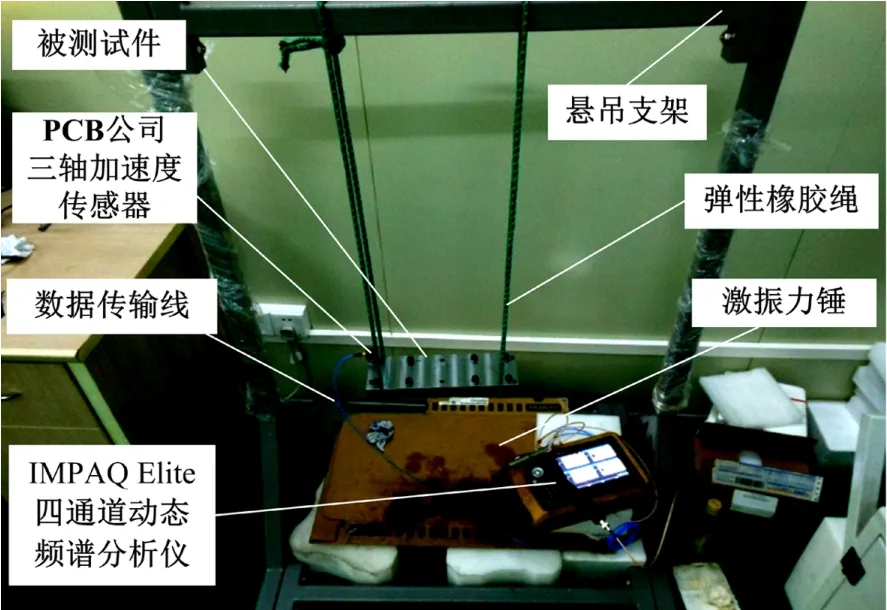
图3 测试现场
2.2 固定结合面的实验模态分析
2.2.1 响应点与实验模型的建立
响应点的数目取决于所选分析频带、期望的模态阶数,以及被测件上所关心的区域。为使响应点在试件上某种程度地均匀分布较理想,通常在感兴趣的区域可多布置几个响应点,测点越多,越能充分表征试件结构的固有模态属性,但测点过多增加测试的困难,加重数据分析处理工作。
综合考虑实验测量的方便性与激励模态的完整性,将上下两个子结构(UP/DOWN)分别划分为32个节点,如图4所示。同时,考虑模态实验时测试点所采集的信息有较高的信噪比,因此测试点不应该靠近节点(节点处振幅为零,能量为零,SNR低)。测试时,选取Node 1作为坐标原点,选定激振点之后,采用模态力锤进行单点激振,在图4所示的各个节点上采用三轴加速度计测量激振时的响应。
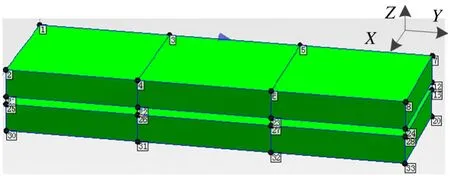
图4 试验测点布置图
2.2.2 信号的采集与处理
频响函数是模态参数频域识别的重要数据。为保证测试参数的可靠性与精度,对频响函数采用多次测试求平均方法,以减小因噪声污染而引起的误差,使频响函数曲线尽可能的光滑。同时,采用相干函数评价频响函数估计精度的一个重要数据,工程上常用其来评价频响函数的测量质量。
相干函数反映了激励和响应两信号之间的相干关系,其取值在0和1之间变化。相干函数等于1,表明激励与响应两信号存在着良好的线性关系,响应信号几乎完全由对应激励引起,可以充分相信频响函数的测量结果。相干函数等于0,表明实测响应信号与实测激励信号完全无关,系统存在严重的噪声污染,湮没了激励信号。一般认为相干函数≥0.8时,表明频响函数的估计效果就比较准确可靠。
试验固定结合面试件的联接螺栓为8个,预紧力矩为30 N·m,结合面无介质。图5为测试得到的频响函数曲线,图6为相应的相干函数曲线,根据相干函数曲线的优劣,可以评价测试过程中的频响函数曲线的质量,进而对频响进行权衡取舍。
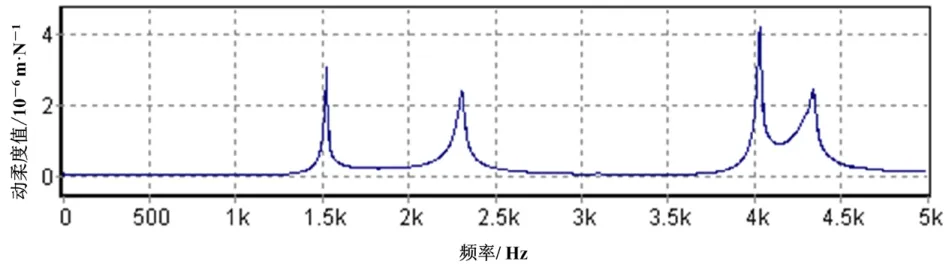
图5 频响函数曲线图
2.2.3 固定结合面试件的模态参数提取[6]
ME’scope(Mechanical Engineering Oscilloscope)是一系列试验的分析工具,能够很容易地进行观察分析和记录设备机械结构的动态特性。
通过Impaq Elite中的FFT模块完成试件实验数据采集,利用ME’scope进行模态分析,提取分析带宽内所关心的固有频率和动柔度值。
分析图5实验测得的频响曲线可知,试件的各阶模态耦合较小、不密集,故采用单模态识别法识别含结合面的试件结构的固有频率和模态振型。所谓单模态识别法是指一次只识别一阶模态的模态参数,所用数据为该阶模态共振频率附近的频响函数值。对其余模态的影响可以全部忽略或简化处理,待识别的该阶模态称为主导模态。将所有关心模态分别作为主导模态进行单模态识别,可得系统各阶模态的模态参数。在FFT模块中提取模态参数的见图7,各阶固有频率列入表2。
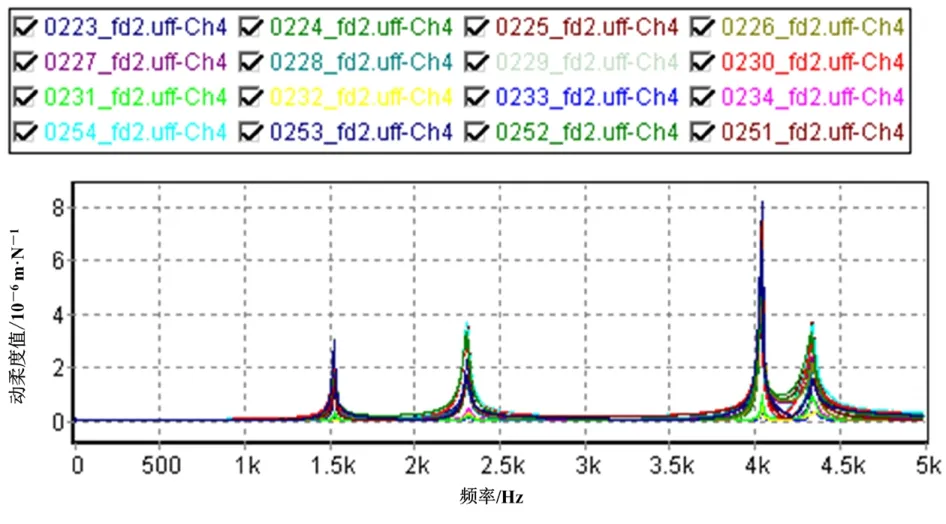
图7 模态参数提取图
3 有限元模态分析
模态分析用于分析结构的动态特性,即确定结构的固有频率和振型等参数。Solidworks Simulation是一款基于有限元技术的设计分析软件[7]。
实体模型在Solidworks软件中完成,在建模过程中可以对其中的一些细节进行必要的简化和忽略。有限元分析软件使用Solidworks Simulation,该软件可完全整合到Solidworks设计分析系统中。因此,建立的结合面模型可以直接导入Solidworks Simulation进行网格划分和分析。网格划分见图8。
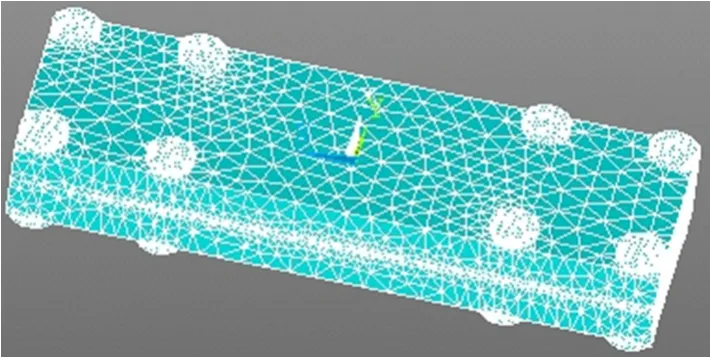
图8 网格划分
试件材料为HT250铸铁,弹性模量E=10.0×10-10GPa、密度ρ=7 100 kg/m3、泊松比μ=0.25。模态计算是自由振型,即取消所有约束条件。网格划分见图8。
通过对8螺栓联接试件模型的有限元仿真分析,计算得到前四阶自由模态的固有频率列入表2,振型见图9。表2数据表明,使用有限元方法所得固有频率与实验模态测得固有频率误差≤8%,可认为两种方法测试结果基本吻合,反映了试件的真实动态特性。
其他实验均采用同一实验设备进行,试件结合部机械结构不变,仅改变结合部介质或螺栓预紧力,因此,认为所测得的动柔度值可信,符合正交实验评价指标一致性要求。
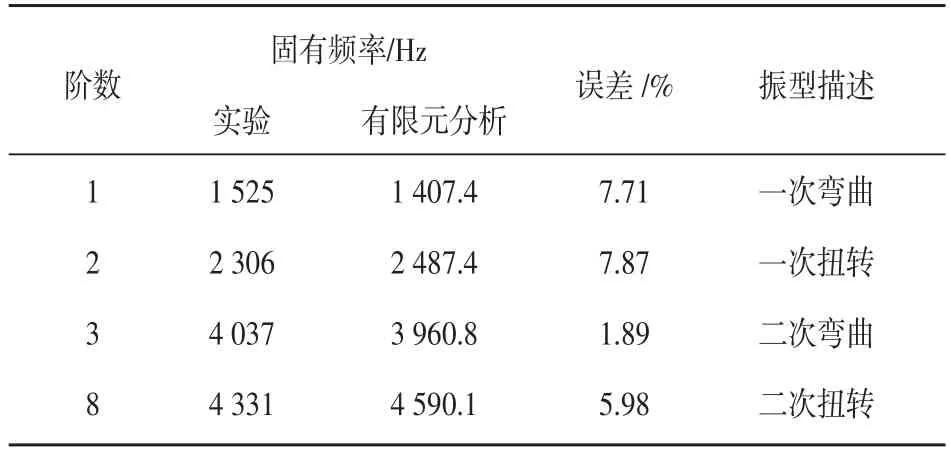
表2 机械结合部实验测试与有限元分析对比
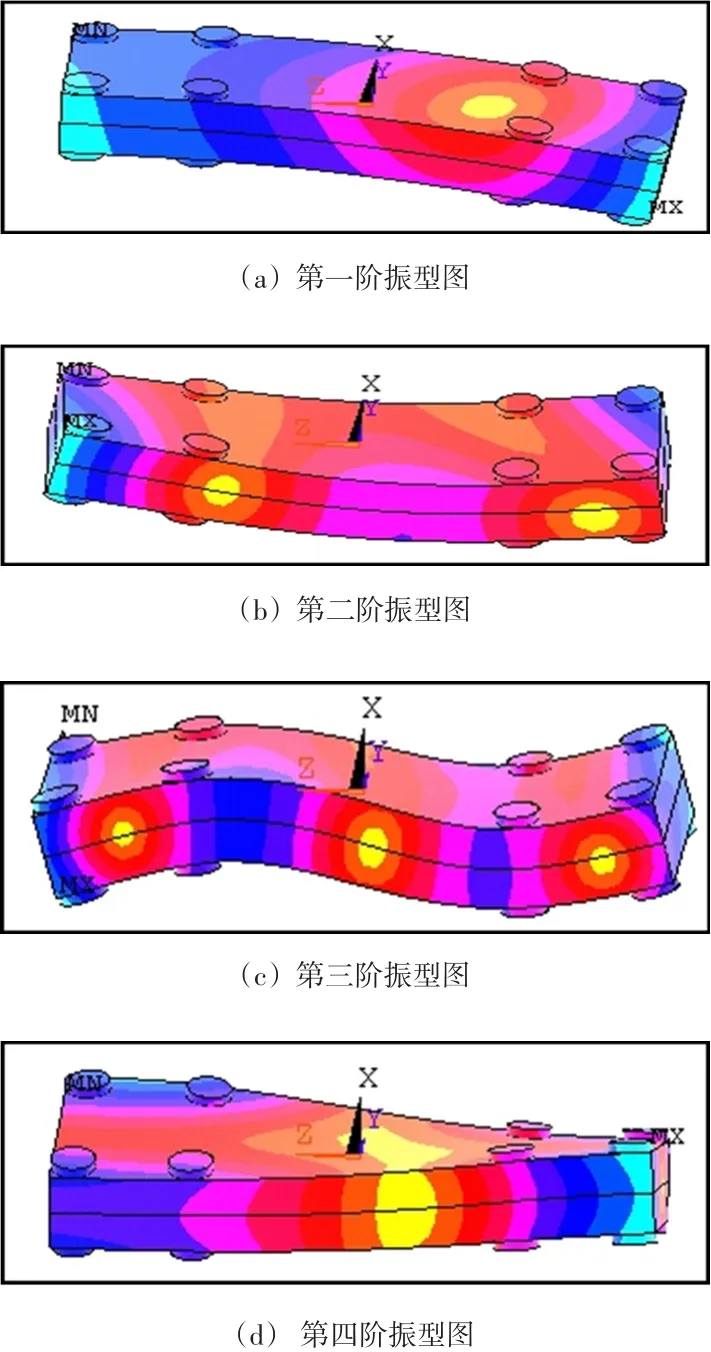
图9 机械结合部前四阶振型图
4 正交试验
4.1 试验设计[8-10]
本文采用正交试验法(Experimental Design)设计实验,分析计算方便,可用较少的实验次数,较快的处理实验数据,获取试验结果动柔度值进行评价。结合面实验变量水平编码见表3。

表3 结合面实验变量水平编码表
本文研究的影响因素有结合部螺栓预紧力矩(X1)、结合部螺栓个数(X2)和结合部介质种类(X3)三个因素,每个因素有三水平,此时可以选用的正交表为L9(34)或L27(313)。试验主要分析三因素对结合部动柔度的影响,对各因素间的交互作用暂不考虑,故选用L9(34)正交表,其中一列赋闲,见表4,表2中所填内容可参看表5。
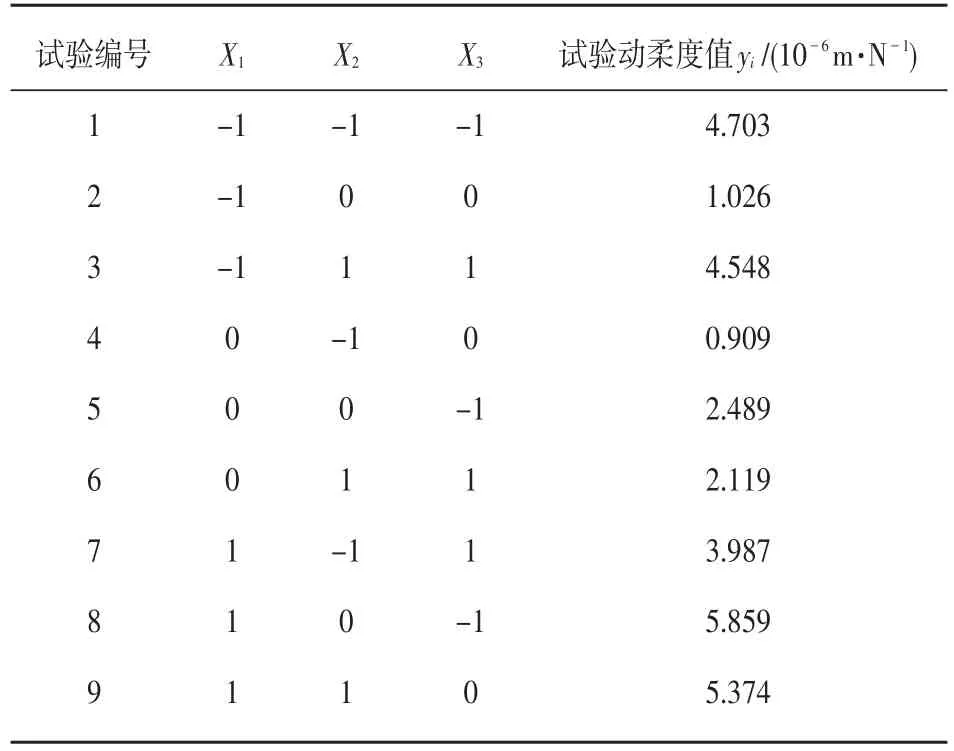
表4 3因素3水平的正交试验结果表
4.2 试验结果与分析
为研究各因素对结合部动柔度的影响效果,对表2中3个因素进行极差分析,再依据极差分析结果进行影响影响大小的排序。实验模态分析结果列入表3,表中Kij表示第j列上水平号为i时的试验结果之和;为第j个因素取i水平进行试验,得到结果的平均值,即其中n为第j因素的水平号为i时出现的次数;极差计算公式为:极差越大说明该因素对试验结果的影响越大,该因素越重要。根据正交试验设计的基本理论,计算得:R1=3.234,R2=0.889,R3=1.791。比较可得,各因素对结合部动柔度的影响效果的排序为:R1>R3>R2。
通过上述比较说明,在本文所研究各因素范围内,影响结合部动力学特性的三个因素中,结合部的螺栓个数对结合部的影响最大,结合部介质的影响其次,预紧力的大小在设定的范围内的影响较小。
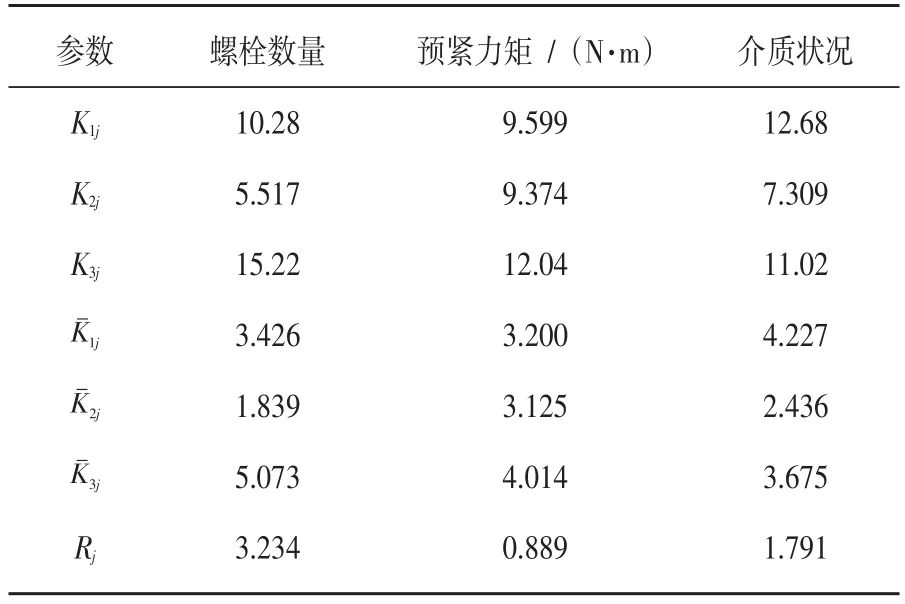
表5 正交试验结果及分析
5 结论
(1)通过对试件结合面动态特性的实验测量,并经过有限元理论分析验证,可判断测试结果可信,即采集的固有频率以及相应的动柔度值基本准确。
(2)由正交试验对结合面在不同影响因素下的动柔度值计算,得出螺栓个数对结合面的动态特性影响最大。
(3)由于结合面是一个非常复杂的问题,本文仅对螺栓个数、螺栓预紧力矩、结合面介质做了研究,且仅做了横向比较。要真正弄清楚结合面的动态特性,必须对其他影响因素进行研究,本文正交试验法在结合面动态特性研究中的应用,为进一步研究结合面动态特性提供参考。
参考文献:
[1]ZHANG G P,HUANG Y M,SHI W H,et al.Predict⁃ing dynamic behaviors of a whole machine tool structure based on computer-aided engineering [J].Internation⁃al Journal of Machine Tools&Manufacture, 2003,43(7):699-760.
[2]张学良.机械结合而动态特性及应用[M].北京:中国科学技术出版社,2002.
[3]张学良,徐格宁,温淑花.机械结合面静动态特性研究回顾及展望[J].太原科技大学学报,2002(3):276-281.
[4]李清国.基于ANSYS的拱架式贴片机整机动力学建模与模态分析[J].机电工程技术,2012(7):72-75.
[5]林剑峰,马晓波,李晖,等.数控机床动态特性测试与分析研究[J].机械制造,2010(8):5-9.
[6]寸花英,袁胜万,田久良,等.TGK46100高精度数控坐标镗床动态性能分析与试验验证[J].机床与液压,2012(17):3-6.
[7]叶友东,周哲波.基于SolidWorks/Simulation的两齿差外啮合双联行星传动系统模态分析[J].机械传动,2015,39(11):103-105.
[8]陈立周.稳健设计[M].北京:机械工业出版社,1999.
[9]任露泉.试验优化设计与分析[M].北京:高等教育出版社,2003.
[10]邓聪颖,殷国富,方辉.基于正交试验的机床结合部动刚度优化配置[J].机械工程学报,2015,51(19):146-153.
