基于自适应遗传算法的空管雷达部署优化*

刘 帅，秦姗姗

（民航西北空中交通管理局宁夏分局，宁夏 银川 750001）

0 引 言

随着民航事业的突发猛进，为了提升民航空管区域管制区、进近管制区的监视性能精度和可靠性，空管部门大规模部署了一二次合装监视雷达、S波段进程一次雷达和L波段远程一次雷达。当前，民航空管在雷达覆盖布站规划中缺乏严谨的、科学的规划方案和手段，简单从补盲的角度出发，设置站点用于填充空域和航路中的盲区，造成部分地区雷达覆盖多重冗余，有的甚至能达到四重覆盖，造成了严重的资源浪费。优化布站是雷达组网的一个重要组成部分，而适当的雷达组网布站可以大幅度提升监视范围，提高监视系统的可靠性和精度。如何在有限的空域和雷达资源下科学确定多部雷达的部署位置，最大范围覆盖空域，构建合理冗余度的覆盖重点管制区，以达到整个雷达网的效能最优，是优化雷达布站的首要任务。本文针对民航空管监视要求，给出了雷达组网优化部署的原则，分析了探测范围、空域覆盖冗余度等，并将部署原则量化成指标，进而建立了更加合理的雷达布站数学模型。

优化布站是一种多约束、多目标组合优化问题。遗传算法在多目标优化的各个方面得到了应用。文献[1]提出利用遗传算法对雷达布站进行优化，但该算法局部搜索迟钝，会陷入局部最优。本文提出了带有精英策略的自适应遗传算法，可快速收敛于全局最优。利用自适应遗传算法对该问题进行求解并仿真，得到了在给定雷达资源情况下合理规划雷达的部署。仿真结果表明，带精英策略的自适应遗传算法满足约束条件，符合部署原则，且在解决问题时具有更高的效率。

1 空管雷达组网系统模型优化

1.1 空管雷达组网约束条件

在空管雷达组网中，将需要覆盖的空域划分为区域管制区和进近管制区。在雷达数目和性能确定的条件下，要求区域管制区最大化覆盖，进近管制区需要至少达到双重冗余覆盖[2]。因此，空管雷达组网模型要满足以下约束条件。

约束条件一：区域管制区覆盖最大化。用Ag表示区域与管制区某一高度层面积，定义空域覆盖系数ρ，表示区域管制区的空域覆盖最大探测范围，则在某一高度层其覆盖系数为：

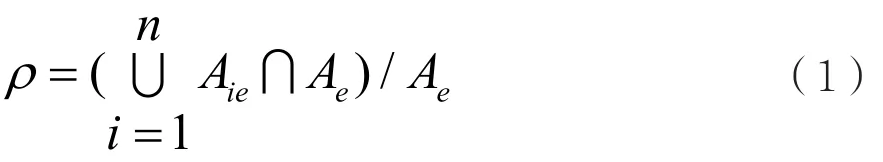
其中Ai表示第i部雷达在当前高度层的覆盖范围，i=1,2…n。

约束条件二：进近管制区能且只能达到双重覆盖。用Ac表示进近管制区某一高度层面积，定义冗余覆盖系数η，表示进近管制区内雷达冗余覆盖系数。在进近管制区，考虑双重冗余覆盖为最佳覆盖，三重级以上覆盖均为资源浪费。因此，某一高度层进近管制区的冗余覆盖系数为：

其中，i＞j＞ k，Aic、Ajc、Akc表示第i、j、k部雷达在重点管制区的覆盖范围。

约束条件三：民航MH/T 4003.2-2014《民用航空通信导航监视台（站）设置场地规范第2部分：监视》文件中明确规定，近程一次监视雷达于无线电辐射工业设施最小保护间距为0.80 km[3]。

1.2 空管雷达组网优化模型

N部雷达组网需要获得尽可能大的区域管制区覆盖范围和进近管制区双重覆盖率。理论上，区域管制区覆盖率和进近管制区双重覆盖率是矛盾的。考虑区域空域覆盖率、进近管制区冗余覆盖率和雷达规范标准，采用加权法将多目标优化转为单目标优化问题，则空管雷达组网模型为：

其中，ρ为区域管制区覆盖率，η为进近管制区双重覆盖率，λ为进近管制区重要系数。

2 自适应遗传算法

标准遗传算法采用选择、交叉好变异算子模仿自然界生物遗传的特性，以选取适应自然的个体，已成功应用于各个领域。但是，它具有局部搜索迟钝、随机游走和局部收敛等问题，导致算法收敛性差。Rudolph利用有限马尔科夫链证明了遗传算法不能收敛到全局最优值。De Jong在其博士论文中提出了“精英选择（Elitist Selection or Elitism）”策略。精英个体是种群进化到当前为止遗传算法搜索到的适应度值最高的个体。精英选择是指在每代种群中出现的最优个体将直接进入下一代种群，不受遗传算子的影响。具体算法实现中，利用种群中的最优个体代替下代中的最差个体，实现种群数量的恒定。Rudolph已经从理论上证明了具有精英保留的遗传算法是全局收敛的[4-5]。因此，本文利用带精英策略的自适应遗传算法（Adaptive Genetic Algorithm，AGA）进行雷达组网优化。

AGA算法流程如图1所示。根据现实情况进行染色体编码，随机生成种群，通过特定适应度对个体进行评价，并存储最优个体。通过选择、交叉、变异3个遗传算子完成种群的遗传操作，生成新的子代。利用父代最优个体替换子代最差个体，实现精英保留策略。同时，利用父代的最大适应度、最小适应度和平均适应度，自适应调整交叉概率和变异概率，解决标准遗传算法的局部收敛和随机发散问题[6]。

AGA算法在雷达组网优化中的实现步骤具体如下。

（1）初始化AGA算法参数，主要包括种群规模、最大遗传代数、个体交叉概率和染色体变异概率等。

（2）染色体编码。染色体编码一般有实数编码和二进制编码两种，本文采用二进制编码，对每部雷达的(x, y)坐标均进行二进制编码。假设N部雷达的坐标组成一组染色体，其需要覆盖的范围为L×L，LSB=0.01，则二进制编码的位数为Nbits=log2(L/LSB)，染色体总体编码为((x1,y1),(x2,y2),…,(xn,yn))，长度为2nN bits。

图1 AGA算法流程

（3）自适应遗传操作。自适应遗传操作主要包括选择算子、交叉算子和变异算子。本文采用锦标赛选择算子，随机抽取个体A和个体B，然后根据个体A和个体B的适应度值，选择其中适应度值最好的个体进入子代种群。精英算子则将每代最佳个体直接保留至下一代，用来替代遗传操作后适应度最低的个体。交叉算子和变异算子用于遗传交叉和变异。过小的交叉概率pc和变异概率pm会导致算法陷入局部最优解；过大的pc和pm会导致算法近似于随机算法，从而发散过大失去遗传算法意义。AGA算法根据每一代种群的平均适应度，自动调节当代种群的交叉概率pc和变异概率

其中，f'为待交叉个体较大的适应度，f为待变异的个体适应度，favg为种群平均适应度，fmax为种群中最大的适应度，k1,k2,k3,k4∈[0,1]。

（4）适应度函数。适应度用于评价遗传种群中个体适应环境的优劣程度。在雷达组网自适应遗传算法中，直接选取雷达组网模型函数f作为适应度函数，对每个个体在区域管制区覆盖率和进近管制区双重覆盖率方面做出优劣评价。适应度越高，说明该个体越优。

3 仿真分析

假设某一区域管制区范围为500 km×500 km，进近管制区范围为100 km×100 km，且该区域由4部不同型号雷达进行组网覆盖。在2 400 m、6 800 m、10 000 m高度层，假设4部雷达探测范围均为圆形区域，雷达A的探测范围为130 km、270 km、350 km，雷达B的探测范围为100 km、200 km、300 km，雷达C的探测范围为80 km、150 km、200 km，雷达D的探测范围为120 km、220 km、280 km。进近管制区重要系数λ=0.6，最小交叉概率pc∈[0.6,0.9]，变异概率pm=[0.001,0.01]，染色体长N=2×4×16=128位，算法迭代代数200，初始化种群100。于是，3个高度层200次的迭代结果如表1所示。

表1 三个高度层AGA算法迭代结果

200次迭代后，2 400 m高度层最优个体适应度为0.847 53，区域管制区覆盖率仅为49.177 5%，进近管制区双重覆盖率达到100%，即进近管制区全部区域均为双重覆盖；6 800 m高度层最优个体适应度为0.987 23，区域管制区覆盖率为95.941 6%，进近管制区双重覆盖率为99.991 5%；10 000 m高度层最优个体适应度为1.0，区域管制区覆盖率为100%，进近管制区双重覆盖率达到100%。2 400 m高度层适应度低，覆盖率低是因为空管雷达在低高度层最大作用距离较小。

在2 400 m、6 800 m、10 000 m高度层的每代平均适应度如图2所示。由图2可以看出，2 400 m高度层在0～50代适应度迅速上升，50～126代出现抖动，126代达到最优解0.847 53；6 800 m高度层在0～159处于搜索上升期，159代达到最优解0.987 23；10 000 m高度层在进化初期适应度迅速上升并达到1.0，后续由于个体变异在140～150代出现了局部平均适应度下降的抖动，150代后重新达到全局最优解。

图2 三高度层AGA算法平均适应度

图3 、图4、图5分别为高度层2 400 m、6 800 m、10 000 m高度层的组网优化效果图，其中黑色矩形区域为进近管制区。

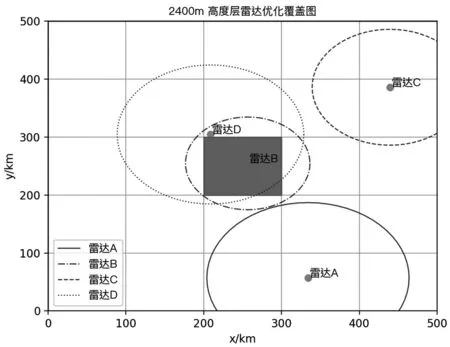
图3 2 400 m高度层组网优化效果

图4 6 800 m高度层组网优化效果

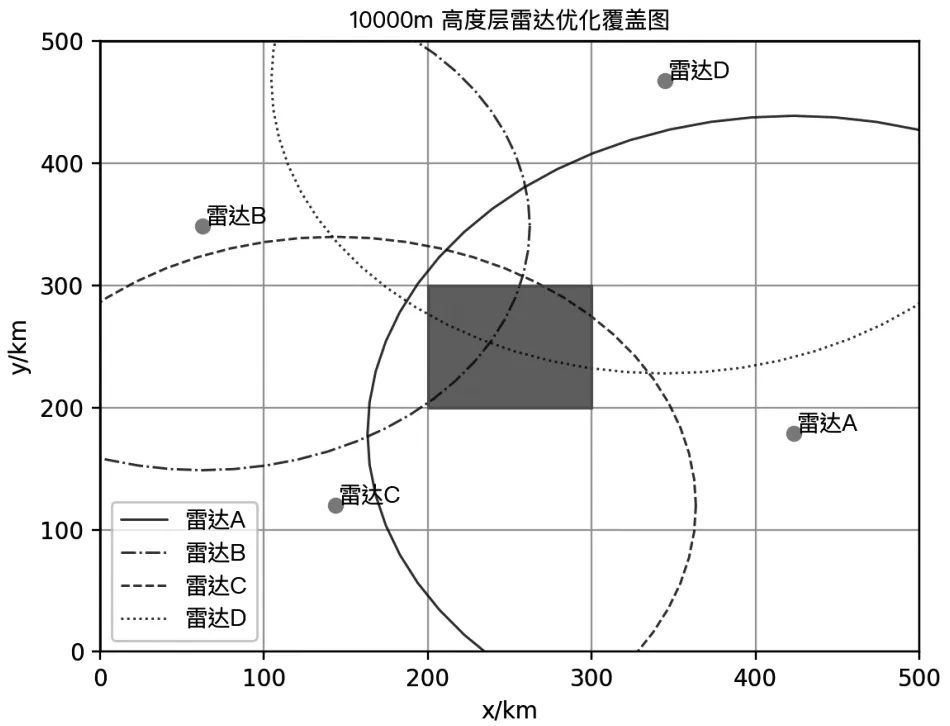
图5 10 000 m高度层组网优化效果

4 结 语

本文分析了当前民航空管监视雷达部署方面造成的空域覆盖率低、雷达利用率低等问题，建立了雷达优化部署方案，提出利用自适应遗传算法进行雷达部署优化。仿真结果表明，自适应遗传算法能够在要求空域范围内迅速收敛于最优解，且得到的雷达部署方案能够有效指导现实雷达部署规划，提高了组网优化效率。但是，该雷达部署数学模型在雷达作用距离方面没有考虑现实地理环境对雷达作用距离的影响，也没有考虑有限管制区域多部雷达之间的电磁兼容对雷达作用距离的影响。因此，今后的工作重点为基于电磁兼容的复杂环境下空管监视雷达的部署优化问题。

参考文献：

[1] 杨仕明,柯炳清,薛正辉.基于遗传算法的区域雷达网优化布站方法[J].北京理工大学学报,2005(06):534-537.YANG Shi-ming,KE Bing-qing,XUE Zheng-hui.Optimized Deployment Method of Regional Radar Network Based on Genetic Algorithm[J].Beijing Institute of Technology,2005(06):534-537.

[2] 高尚.雷达部署优化模型[J].应用科学学报,2006(04):437-440.GAO Shang.Optimization Model for Radar Deployment[J].Journal of Applied Sciences,2006(04):437-440.

[3] MH/T 4003.2-2014 民用航空通信导航监视台(站)设置场地规范第2部分:监视[S].2014.MH/T 4003.2-2014 Specification for Aeronautical Communication,Navigation and Surveillance Station Siting Criteria Part2:Surveillance[S].2014.

[4] 付鑫,张峰,冯占林.基于并行计算的混沌遗传算法对反导预警雷达部署优化研究[J].中国电子科学研究院学报,2016,11(03):276-282.FU Xin,ZHANG Feng,FENG Zhan-lin.Research of Chaos Genetic Algorithm Based on Parallel Computing for Anti-Missile Warning Radar Dispositon[J].Journal of CAFIT,2016,11(03):276-282.

[5] Fauzi M J.A Review of Genetic Algorithms and Parallel Genetic Algorithms on Graphics Processing Unit(GPU)[C].IEEE International Conference on Control System,Computing and Engineering(ICCSCE),2013.

[6] 曹洁,张玲.自适应遗传算法的Multi-Agent交通信号优化控制[J].计算机工程与应用,2016,52(13):265-270.CAO Jie,ZHANG Ling.Multi-Agent Traffic Signal Control Based on Adaptive Genetic Algorithm[J].Comupyter Engineering and Applicatinos,2016,52(13):265-270.

[7] KONG Hai-peng,LI Ni,SHEN Yu-zhong.Adaptive Double Chain Quantum Genetic Algorithm for Constrained Optimization Problems[J].Chinese Journal of Aeronautics,2015,28(01):214-228.

[8] 张玉萍.自适应遗传算法的研究及应用[D].哈尔滨:哈尔滨工业大学,2009.ZHANG Yu-ping.Research and Application of The Auto-Adapted Genetic Algorithm[D].Harbin:Harbin Institute of Technology,2009.