一种基于新型特征与支持向量机的调制识别方法*
2018-05-05陈佳林
陈佳林,熊 刚
(1.海军研究院,上海 200436;2.中国电子科技集团公司第三十研究所,四川 成都 610041)
0 引 言
随着现代通信系统的发展,信号调制识别算法发挥着越来越重要的作用。确定信号的调制类型,是实现对通信信号接收解调的前提条件。因此,信号调制识别技术在民用和军事领域的应用十分广泛。2017年,美国国防高级研究计划局DARPA举办了被称为“调制识别之战”(Battle of the Mod Recs)的活动,探索了一些新的无线信号类型识别的解决方案,并认为调制识别是电磁空间态势感知的关键之一,有助于从拥挤的频谱中挖掘出更多潜力。在认知无线电方面,调制识别算法能够在缺乏先验信息的情况下分析得出信号的调制样式,有助于进一步估计出信号的其他参数,为完成频谱空洞检测和动态频谱接入打下基础。此外,调制识别算法还可用于频谱监测和管理、干扰判别等方面,已引起国内外学者和研究机构的广泛关注[1]。
信号调制识别思路一般基于两类判别原则,即决策理论和统计模式识别。由此,调制识别算法可相应分为基于决策理论的方法和基于统计模式的方法。根据决策理论提出的方法主要是研究分析信号的统计特性,利用概率论和假设检验原理得出统计量。此类方法的主要做法是求取最优解,但计算复杂度较高。学者Azzouz和Nandi曾提出一种基于特征决策的识别算法,需要计算确定每种调制样式的具体决策门限,从而满足决策树判断的需要。基于统计模式的识别方法近年来得到较大发展,其处理步骤更加灵活,可较易得到合理的判决门限,比基于决策理论方法的运算量小。
基于统计模式的方法一般包含特征提取和分类两部分。典型的识别分类器结构有支持向量机(SVM)等,可以很好地实现调制类型区分。此外,人们通过研究各种新特征提取方法,得出如高阶累积量特征、瞬时幅度、瞬时频率和相位等信号统计特征[2]。但是,单一类型特征的稳健性不够理想,需综合利用以进一步提高识别性能。
针对以上问题,本文在统计模式思路的基础上,提出了一种基于新型特征与支持向量机的调制识别改进方法。该方法将提取到的时域、频域和小波变换域等方面特征进行融合计算,具有在低信噪比条件下较优越的性能。在分类判决环节,基于支持向量机和改进的分层模型判决思想,提高了分类识别的准确率。该方法的抗噪性良好、通用性强,可识别多种数字调制样式,包括2ASK、4ASK、2FSK、BPSK、QPSK、8PSK和16QAM等。
1 信号模型分析
数字通信调制信号模型的数字表达式一般可表示为:
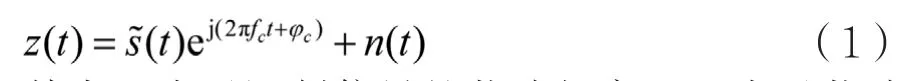
其中fc表示调制信号的载波频率,φc表示载波相位,n(t)表示加性高斯白噪声。s~(t)为信号s(t)的基带复包络表达式,定义如下:

其中a(t)、f(t)和φ(t)分别表示调制信号的瞬时幅度、瞬时频率和瞬时相位。
图1表示信号调制识别的总体流程框图。首先将接收到的调制信号送入预处理模块进行幅度归一化、滤波等处理,然后通过特征提取模块提取各种统计特征。
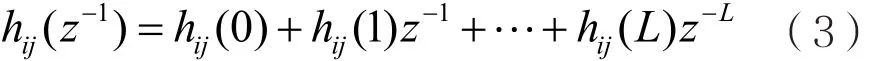
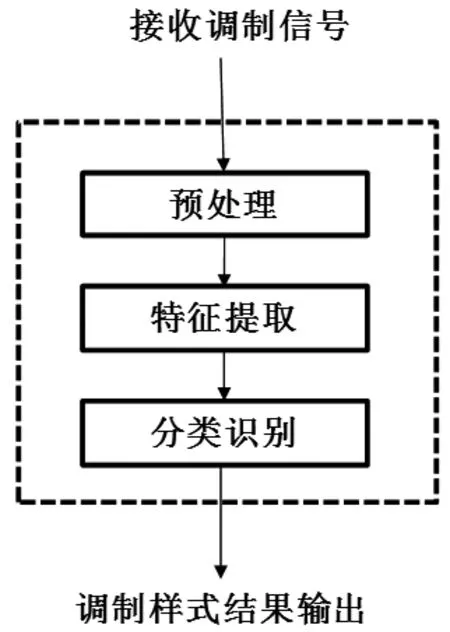
图1 信号调制识别总体流程
调制识别算法中有用的特征可以从归一化信号的时域、频域和小波变换域获取。其中,利用小波变换可以较好地去除噪声影响,在低信噪比环境中从信号自身提取出一些辨识性更好的新型特征,精确反映出实际细节;在分类判决部分,过去传统的结构是一对一(OAO)结构,可以对常见通信信号调制样式进行归类,但该结构相对复杂。
2 算法分析和改进
2.1 特征提取思路分析
特征提取是调制识别算法的重要环节,也是后续分类判断的前提和基础。从数字通信信号中提取的调制特征,应满足不易受噪声变化影响的需要[3]。
本文对一些新型信号特征进行了研究,主要包括时频域和小波变换域两方面特征。
2.1.1 时频域特征
经过分析和优选,提取了3种时域特征和1种频域特征,适用于幅度调制信号、频率调制信号和相位调制信号的识别。
(1)瞬时相位非线性分量的二阶矩该特征的数学计算表达式为:

其中φNL表示瞬时相位的归一化中心非线性分量,为:

(2)接收信号段的归一化瞬时幅度功率谱密度均值
该特征的数学计算表达式为:
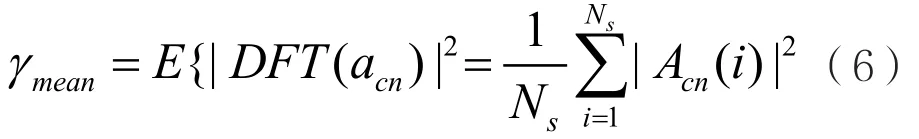
其 中 Acn=DFT(acn),acn表 示 在 时 刻 t=i/fs,(i=1,2,…,Ns)的归一化中心瞬时幅度,定义为:

式中的ma表示对该信号段瞬时幅度估计出的均值,计算表达式为:

其中Ns表示信号采样点数,a表示接收信号的瞬时幅度。该特征参数可用来较好地区分2ASK调制信号与4ASK调制信号等。
(3)加窗处理瞬时相位归一化中心非线性分量标准差
该特征的数学计算表达式为:
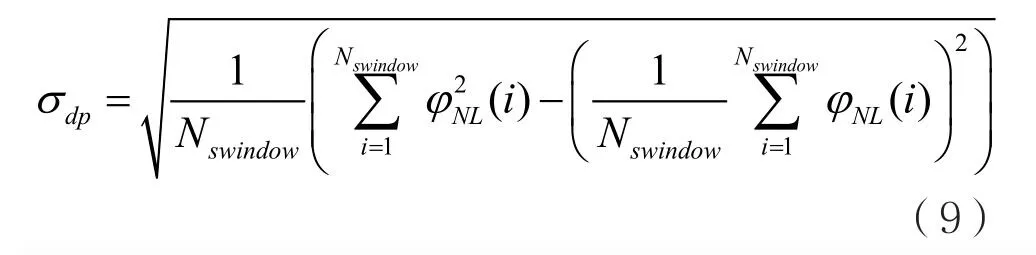
其中φNL表示对信号加窗处理后的瞬时相位归一化中心非线性分量,Nswindow表示在对应窗长度内的信号样本点数。计算该特征时,对Azzouz和Nandi两位学者提出的方法进行了改进,选取合理的窗函数(典型为hamming窗)对信号加窗平滑处理,可用来更加稳定地区分BPSK调制信号和QPSK调制信号。
(4)信号频谱新型特征
该特征的数学计算表达式为:
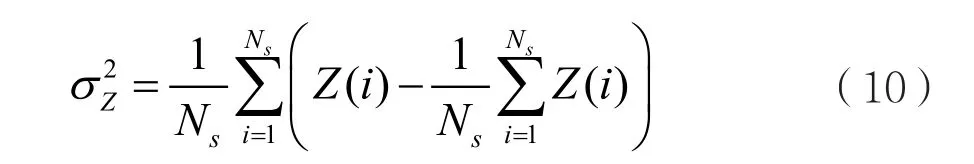
其中Z(i)表示接收信号的傅里叶变换分析表达式,Ns表示信号的采样点数。这种新型特征可用来提取信号包络信息,从而区分FSK、PSK和ASK、QAM信号。
2.1.2 小波变换域特征
小波变换可以根据不同情况对信号实现不同分辨率频率的分析,并能更精确地提取出非平稳信号的重要细节特征。一些抗噪性优越的特征仅能从小波变换域中获取,无法由其他变换得到。本文中,连续小波变换(CWT)用于从接收信号中提取可分离的特征,定义如下:
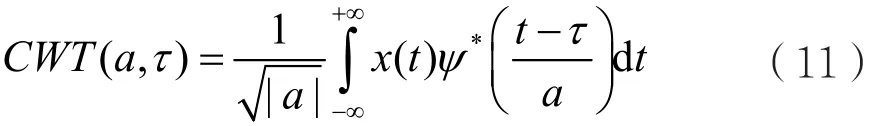
其中ψ(t)表示小波基,ψ*表示其复数共轭,a≠0表示尺度因子,τ表示位移因子。通常,选择Harr小波函数作为连续小波变换的基函数。它具有良好的正则性、对称性和理想的频域局域化特性。
Harr小波函数的定义如下:
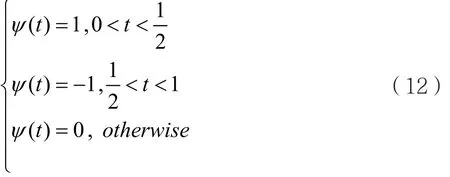
尺度因子的数值代表小波基ψ(t)进行压缩或扩展的数量,各级尺度可由2m表示,其中m为预定义常数。下面进行ASK调制信号的Harr小波变换,可得出其计算模板表达式为:
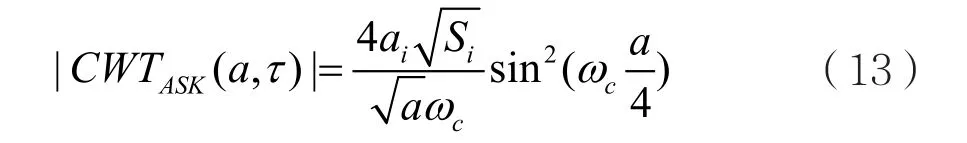
且得到FSK调制信号的Harr小波变换计算模板表达式如下:
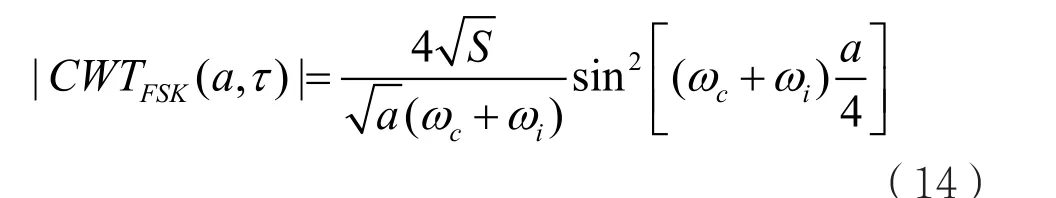
下面对新改进的两种小波变换特征提取思路说明如下:
(1)接收到信号后,将其幅度归一化为1。本文选取64级尺度(即m=6)计算连续小波变换的系数。
(2)使用Haar小波(HWT)在尺度为1至64处分别计算接收信号的CWT结果,得到一个64行、Ns列的矩阵,其中Ns是数字化接收信号中的采样点数。
(3)将接收到的信号在小波域中与存储的调制样式分析模板进行匹配,并计算接收信号和该模板的互相关值。如果接收信号的HWT是一个64×Ns矩阵而模板是一个64×2Nb矩阵,那么它们之间的尺度互相关结果为64×(Ns+2Nb-1)的矩阵,且每行是相应尺度的互相关结果,其中Nb表示每个符号的持续时间。
(4)根据相关运算的结果进行识别。若结果在同一级别,表明模板的共同特征明显,可增强其抗噪性能。
2.2 分类器思路分析
支持向量机(SVM)是一种典型的机器学习算法,常用于对数据进行分类。SVM算法可以避免由于局部最小导致的二次问题,从而将未知测试样本与训练样本的误分类风险降到最低[4]。在线性SVM算法中,设数据集D中含有n个训练样本点,定义如下:
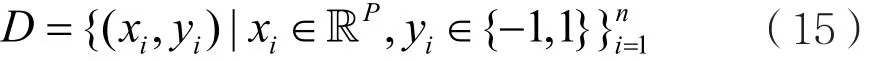
其中各输入xi表示P维向量,且属于两个分类面yi=-1或+1之一。
SVM的目的是寻求可用于分离的超平面,使得两类的分类间隔最大。该超平面可定义如下:

其中w表示超平面的模,b/||w||代表从超平面到原点的距离。支持向量是指在2类样本中离分类面最近且平行于最优分类超平面上的训练样本,作用是寻找平行平面彼此之间具有最大距离的w和b。支持向量所在的平面可表示为:

如果训练样本线性可分,则可以将支持向量点中的平行平面及相关问题转化为两个平面之间距离最大化问题。基于几何关系,则间隔等于2/||w||。因此,为了使其间隔最大化,须求||w||的最小值。此外,为了避免样本点扩散到间隔区域,输入数据必需满足:

因此,最优化问题的数学表达式可表示为:

使||w||最小化则等价于使得||ω||2/2最小化,则上述问题又可表示为:
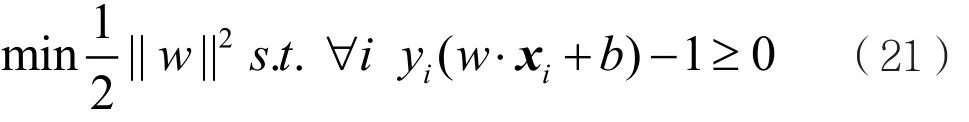
这本质上是一个二次规划问题,可采用拉格朗日乘数法进行求解,处理框图如图2所示。
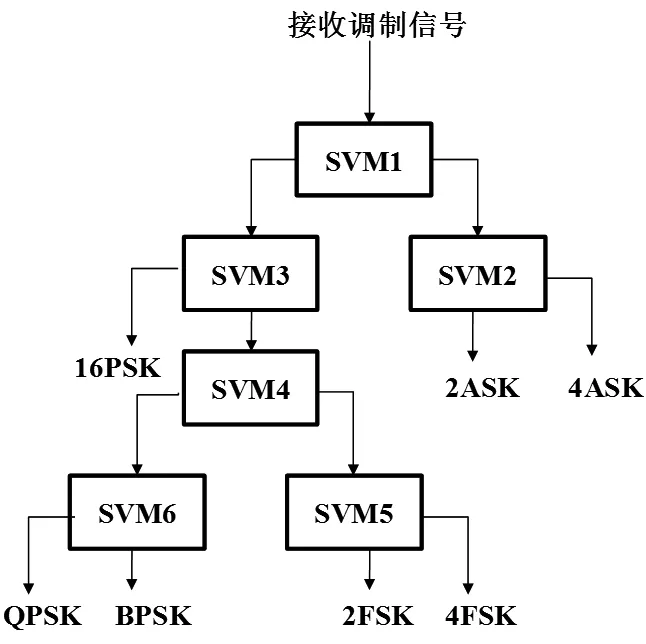
图2 新改进的SVM调制样式分类器
最优分类面的权系数向量是训练样本向量的线性组合,得出:

可进一步推导,支持向量机问题的对偶问题可由优化表示式进行化简:
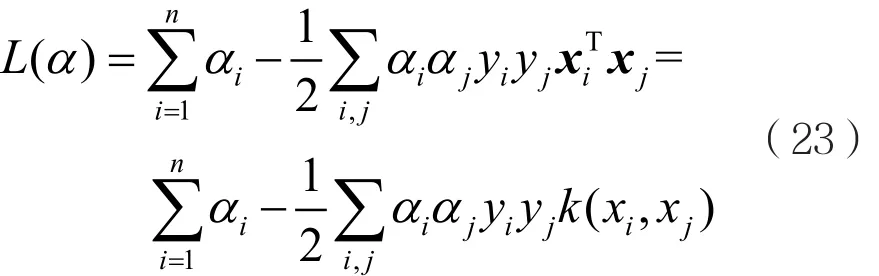
其中,k表示高斯空间的核,αi≥0且i=1,2,…,n。
SVM是一个两类的分类器,本文采用一种新型改进的分层结构,以实现信号调制样式分类的优化。从图2可以看出,该结构是一种决策树与两类支持向量机结合的分类器。对于该结构的每一个节点,都有一个二类支持向量机把输入分成两类。树型分类器较好地融合了各个特征的分类性能,更全面地对目标调制类型信号进行分类判断。
3 仿真结果及性能分析
为了验证本文方法的有效性,采用MATLAB软件开展了以下仿真实验。仿真参数——信号采样率为2 MHz,载波频率为500 kHz,码速率为50 kb/s,信号采样点数为8 192,蒙特卡洛仿真次数为2 000次,噪声为加性高斯白噪声。
仿真实验1:设各信号的调制样式分别为2ASK、4ASK、2FSK、4FSK、BPSK、QPSK、8PSK和16PSK,采用本文中基于新型特征和支持向量机的方法进行识别,得出对信号调制样式的正确识别率。仿真结果如图3所示。
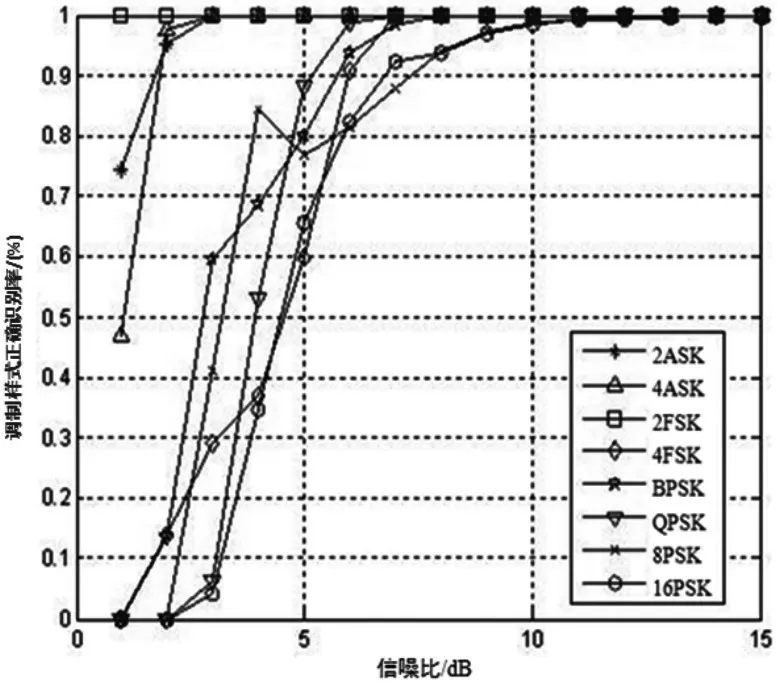
图3 本文方法对各调制样式的正确识别率曲线
从图3可以看出,本文方法是一种有效的调制识别方法,在信噪比大于6 dB时,对各调制样式的正确识别率可达到95%以上。
仿真实验2:分别对传统的基于循环谱的识别算法、基于高阶累积量的方法和本文改进方法进行调制识别性能比较的仿真分析。仿真参数条件和仿真实验1所述相同,仿真结果如图4所示。
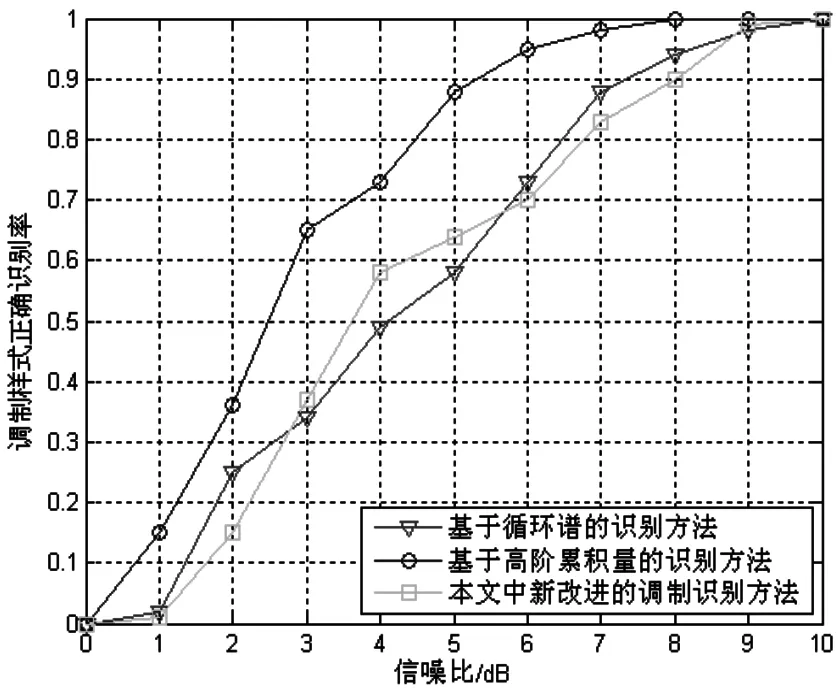
图4 三种方法的调制识别性能比较
由仿真结果可以得出,新方法比过去一些传统的调制识别方法具有更优的识别性能,适用于复杂环境对数字调制信号的处理。
4 结 语
随着通信技术的不断发展,信号的调制类型变得越来越多样化,信号环境也更加复杂化。因此,对于调制样式的识别研究提出了更高需求。本文提出了一种基于累积量的特征融合改进方法。仿真验证表明,该方法相对于传统的识别算法,能够改善调制识别的分析性能。今后将进一步优化,为解决复杂电磁环境中低信噪比的信号调制样式识别问题提供了一种更有效手段,且为网电对抗领域的研究贡献了力量。
参考文献:
[1] Ramkumar B.Automatic Modulation Classification and Blind Equalization for Cognitive Radios[D].Virginia:Virginia Polytechnic Institute and State University,2011.
[2] Hong S,Like E,Tekin C.Multi-user Signal Classification via Spectral Correlation[C].Consumer Communications and Networking Conference(CCNC),2010,7(01):1-5.
[3] Ramkumar B,Bose T,Radenkovic M.Robust Multiuser Automatic Modulation Classifier for Multipath Fading Channels[J].New Frontiers in Dynamic Spectrum,2010,5(09):1-10.
[4] Forero P,Canos A.Distributed Feature-based Modulation Classification Using Wireless Sensor Networks[C].Military Communications Conference,2008,11(03):1-7.
