木纤维脉冲-旋流气流干燥气固两相流分析及数值模拟

陈峰

(辽宁林业职业技术学院，沈阳，110101)

高珣 程万里

(北华大学木质材料科学与工程重点实验室) (生物质材料科学与技术教育部重点实验室(东北林业大学))

气固两相流是管道中的流体(气相)带动固体颗粒或粉末(固相)进行输送和干燥[1]，气固两相流是一项综合性研究内容，涉及诸多学科，广泛应用于发电、化工、水泥、制药、粮食里面的颗粒、粉末或纤维的气流干燥[2]。在干燥过程中的气固两相流具有流动复杂性和测量困难性，基于各相能量、动量守恒定律，可建立反应不同相的流体力学方程，通过计算机计算仿真模拟[3]，这样不仅节约时间，且能反映实验的直观性和可预测性。

国内外有研究人员对于脉冲干燥机和旋流干燥机进行计算流体力学(CFD)模拟的研究[4-5]，但是目前还没有对两者组合起来的脉冲-旋流气流干燥系统的两相间的传热传质过程进行定量的研究。笔者利用理论分析模型建立脉冲-旋流气流干燥传热传质模型，并结合杨木纤维干燥的需求及脉冲-旋流气流干燥特点，利用CFD模拟软件ANSYS Fluent 14.5进行三维模拟，基于欧拉-拉格朗日模型的稀相气固两相流动的数值模拟。通过CFD软件对脉冲-旋流干燥机进行分析，掌握脉冲-旋流干燥过程中的流场、湿度、温度、速度、压力、纤维分布，从而为今后大规模开发该纤维干燥系统提供理论依据。

1 Fluent算法的过程分析与数学描述

1.1 气固两相流体的物理特性参数

对脉冲-旋流干燥气固两相流动实验和仿真，纤维的物性参数直接影响数值计算结果。根据中试设备实际输送的纤维物料测量结果来设置物理特性参数。本研究模拟计算的气相介质为标准气压，干燥温度为200 ℃。

离散相固体颗粒的平均直径0.223 mm。由于纤维形状为非球形，根据以下公式计算得出其形状系数[6]。

式中：Sf为形状系数；R为纤维直径(mm)；h为纤维长度(mm)。纤维长度和直径根据实验测定值来设定，最后计算纤维形状参数为0.593。

干燥介质为空气，根据实验干燥前的测量结果设置纤维的平均粒径、长度和长径比；材料的物理参数包括密度、比热容、导热系数和空气黏度，这些参数根据该材料在指定温度条件下的标准值查表设置(见表1)。

表1 脉冲-旋流气流干燥系统气固两相的物理特性参数

1.2 几何模型的建立和网格划分

本研究主要模拟杨木纤维颗粒相在脉冲-旋流管道中的运动状态和干燥过程，利用Solidworks软件进行建模[7]，实验采用ICEM对脉冲-旋流干燥机进行网格划分。将Solidworks生成的三维实体模型装入到CFD前处理软件ICEM-CFD(ICEM-CFD 14.5，ANSYS Inc.)中对其使用混合网格划分[8]；在划分网格时，对脉冲干燥器采用六面体的结构化网格，过度角部采用非结构化网格来划分。经检查网格质量在0.5以上，脉冲-旋流干燥器生成的网格总数为7 099 656个。

1.3 求解器选择和边界条件设置

选择基于压力的求解器。时间类型选择稳态，速度方程选择绝对速度，模型考虑重力加速度作用，重力加速度为-9.8 m/s2；采用离散型模型，入口边界离散相固体颗粒平均直径0.223 mm；由于纤维形状为非球形，纤维形状参数为0.593。选择平均离散相热量作为热传递系数。选择与连续相耦合来激活双向耦合，每隔此连续相迭代步数值为10。粒子获取形式为进口条件为逃逸，出口条件为捕捉，壁面条件为反射。气相控制方程应用标准K-ε湍流模型来模拟干燥机内部的湍流运动。

1.4 气固两相流求解

使用非耦合隐式算法用于定常流计算，差值计算算法采用一阶迎风格式，设置动量项为二阶迎风格式；将收敛临界的迭代残差标准设为0.001。计算过程中首先假设不带颗粒的空气为连续相，初始化后再对气相流场进行计算模拟，连续相计算2 598步后计算收敛。将带一定含水率的杨木纤维为离散相进行气-固两相耦合模拟，观察气流与杨木湿纤维相互作用的情况。

2 脉冲-旋流气流干燥过程的数值模拟

2.1 气流场的运动和变化规律

图1是设定风机出风口气流的速度为10 m/s，脉冲-旋流干燥气流场速度变化图。图1a为气流进入脉冲-旋流干燥段中的速度分布情况，可以看出气流由脉冲干燥管底部进入由旋流干燥器顶部排除。图1b是脉冲干燥管z=160 mm纵向气流场速度云图，可以看出，气流在直管中呈加速运动，速度逐渐趋于稳定；当管道直径增大，气流速度呈减小趋势，并且减小的趋势逐渐变小；在管道内存在着明显的速度梯度，由于壁面和流体的摩擦存在，越接近管壁速度梯度越大，靠近管道速度小，在管道中心区域流速最大；在气流流经弯管处，速度分布发生了变化，在气流刚进入弯管时，靠近弯管圆心管壁处速度较大，通过速度云图可以看出随着气流在弯管运动，在下降管弯头处速度最大，为15.8 m/s。这是由于气流在弯管处离心作用增大，在靠近弯管内侧气流密度较大，压力场增大，导致靠近弯管内侧的气流速度增大，也与伯努利方程所描述一致。

图1c是旋流干燥器整体气流场流线图，表明气流沿着切线进入到旋流干燥器中，气流呈低速旋转状态，增加了物料在干燥器停留的时间；气流运动到干燥器底部，由内部套管直接加速运动到干燥器出口，这一气流特征会影响杨木纤维在气流场中的运动轨迹。图1d是旋流干燥器y=300 mm横向气流场速度云图，表明干燥器内靠近外侧的速度明显高于中间气流速度，气流在内部套管中速度最大，达到12 m/s。

把脉冲干燥管0～8.4 m轴线作为观察对象，观察10～13 m/s不同进风速度条件下，气流速度变化。从图2可知，气流在0～1.7 m位置加速运动，在1.7～3.5 m位置减速运动，在3.5～3.8 m急加速运动，说明由脉冲管至直管直径突然变小区域速度变化明显；3.8～5.2 m/s时加速幅度减小，但最大风速比0～1.7 m的最大风速要高；之后在5.2～6.8 m时，脉冲管风速再进行减速运动，当风速为13 m/s时，气流在此部分湍流运动明显；在6.8～7.2 m进行二次急加速运动；在7.2～8.2 m再进行加速运动，可以看出在此部分加速度变小，在12 m/s时接近匀速。8.2～8.4 m处，气流进入弯管处气流速度变小。

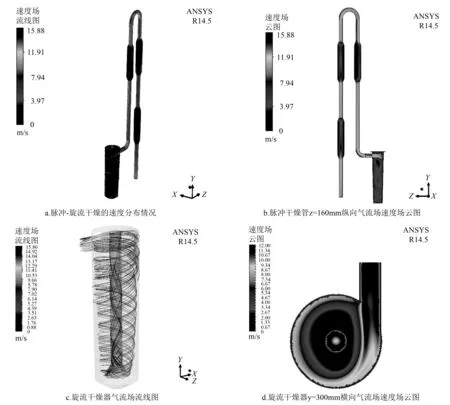
图1 脉冲-旋流干燥气流场速度变化图

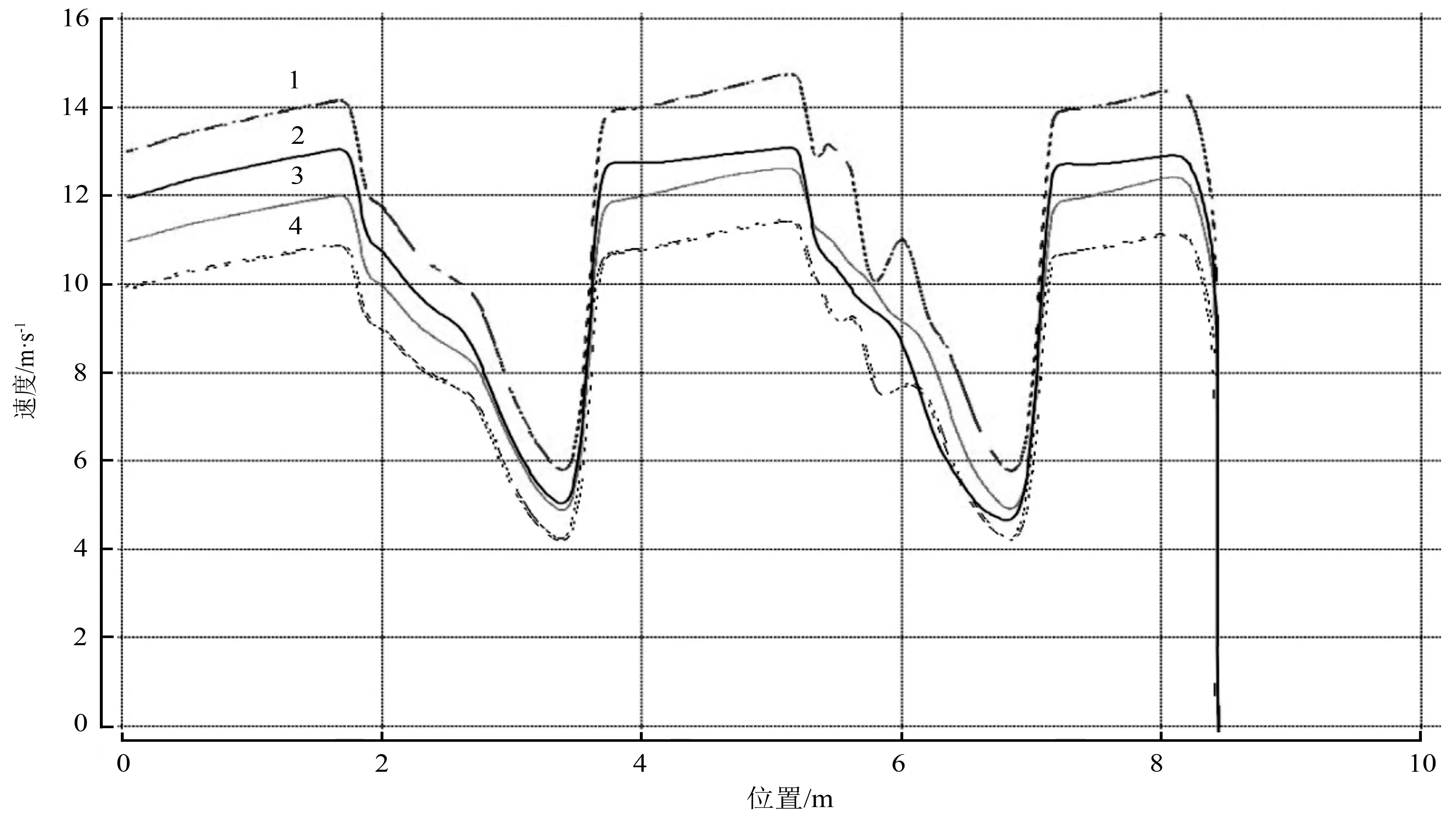
图2 y=0～8.4 m处脉冲管不同进风速度气流场速度变化曲线

2.2 杨木纤维颗粒的运动轨迹

运用非耦合隐式算法得出杨木纤维颗粒的运动轨迹模拟结果。图3a为通过纤维颗粒在脉冲-旋流干燥流场的气流速度分布情况，加入纤维的最大气流速度为13.6 m/s，相对于图1a中未添加杨木纤维的最大气流最大速度(15.9 m/s)降低了2.3 m/s。这是因为杨木纤维与气流之间的温度差，使气流将热量传递给了杨木纤维，气流温度降低。由于固态颗粒占据了管道一部分空间，使得气体所占管道的体积分数变小，从而降低了气流的运动速度，这与前人关于粉煤灰脉冲气流干燥器的模拟结果是一致的[9]；并且当湿纤维进入干燥器中，也在一定程度上降低了气流的速度。从图3b可知，物料最大速度为11.6 m/s，与气流最大速度相差为2 m/s；通过气-固两相之间的速度差强化了木质纤维与热空气之间的对流作用，这有利于提高木质纤维的干燥速率和效果。图3c为脉冲-旋流干燥机中的物料停留时间，物料在干燥机最大停留时间为19.1 s；其中在脉冲管停留时间最短为4.2 s，在旋流干燥器中停留时间为14.9 s。对气流干燥过程进行理论分析可知，在干燥管入口处，初速度为零的杨木纤维被具有很大速度的热空气加速，此时两相间的相对速度最大；同时由于在此处理的纤维较多，即传热表面积最大，因此干燥管入口段的传热传质系数最大，此处的对流传热传质效率远远大于之后的干燥段。由此可知，入口加速段对整个干燥过程的影响最大。

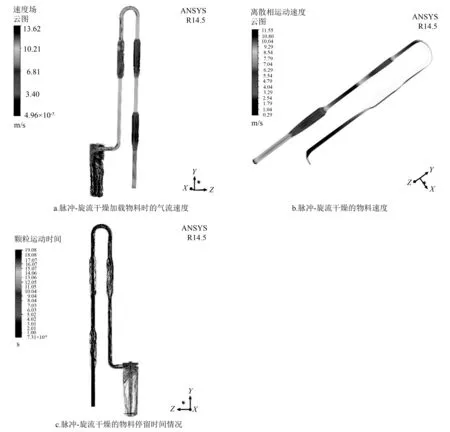
图3 杨木纤维颗粒的运动轨迹模拟结果

图4a为热气流温度变化，图4b为物料温度随着干燥管道长度的变化。可知，200 ℃的热气流在干燥过程开始后，温度不断下降，在进料口处温度下降幅度较大，在第二段脉冲管处温度趋于稳定，最终热气流以181 ℃的温度排出。这是由于气流温度与纤维之间温差较大，传热效果最好；随着气-固两相温差减少，其传热效果逐渐降低。纤维在整个过程中温度不断升高，在干燥过程中，进口为26 ℃的纤维在出口处温度为163 ℃，气流温度一直大于物料温度，说明热气流的热量利用较充分。当管道长度继续增加后，物料和气流温度最终温差为18 ℃，温度变化不明显，说明再增加管道长度对脉冲干燥管的干燥效率影响不大。

2.3 进料速度对脉冲-旋流干燥气-固两相流的影响

图5考查了物料不同喂入量的固相运动轨迹，每条流线代表每个颗粒的运动轨迹，在进料速度不同时，颗粒的运动轨迹也不同，最终位置也不同。进料速度变大，使得气流中的湍流运动变强，纤维之间碰撞几率较大。进料速度增大会导致物料分布不均匀，在旋流干燥器底部容易造成物料返流。当进料速度为0.041 kg/s时，物料在内管处返流更强，且只有少量物料排除，不利于输送物料。结合输送性能分析可知，物料喂入量为0.033 kg/s时是最佳喂入量。

图4 脉冲干燥器z=80 mm横向物料与流场温度云图

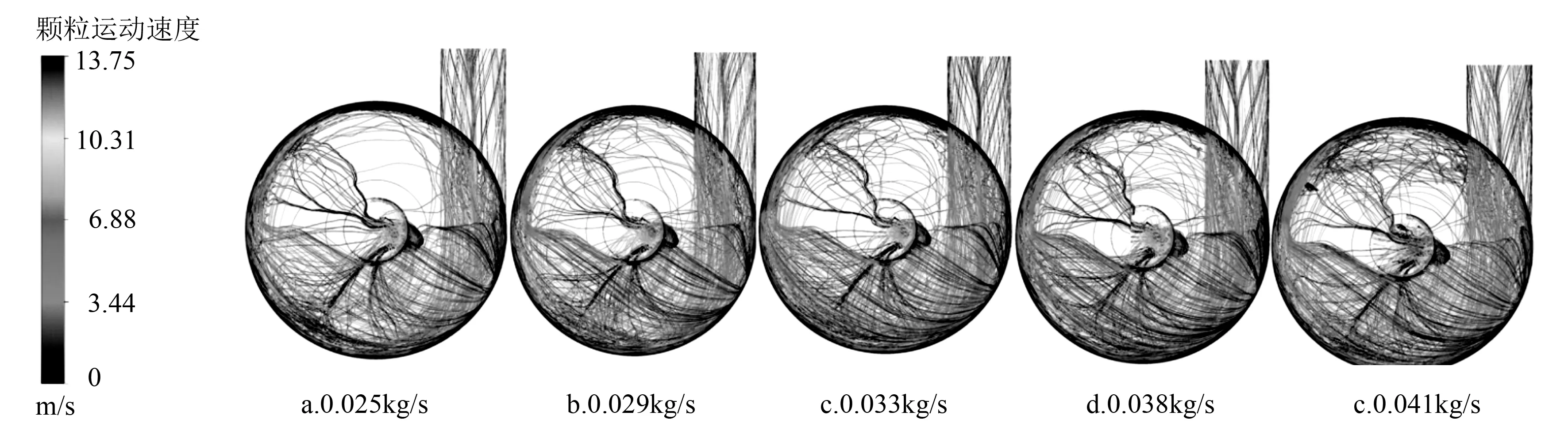
图5 不同进料速度下旋流干燥器杨木纤维颗粒运动情况

2.4 数值模拟验证

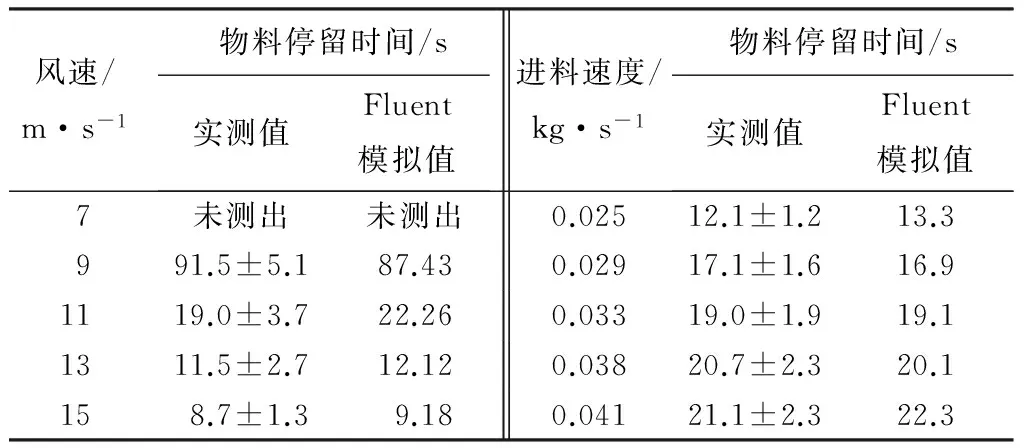
将20 kg物料放入干燥机中，开启干燥机开始计时，出料时结束计时，出料时间与开启时间的差值为物料在干燥机中的停留时间。表2为不同进风速度、进料速度下物料停留时间。在Fluent中模拟物料停留时间，结果表明，数值模拟能够很好地反映物料的停留时间，且计算值和实测值的相对误差都小于10%，变化趋势一致。可见采用欧拉-拉格朗日模型模拟脉冲-旋流干燥器的气-固两相流动的计算结果是可信的。

表2进风速度和进料速度物料停留时间数值模拟结果与实测值对比

风速/m·s-1物料停留时间/s实测值Fluent模拟值进料速度/kg·s-1物料停留时间/s实测值Fluent模拟值7未测出未测出0.02512.1±1.213.3991.5±5.187.430.02917.1±1.616.91119.0±3.722.260.03319.0±1.919.11311.5±2.712.120.03820.7±2.320.1158.7±1.39.180.04121.1±2.322.3

注：实测值为平均值±标准差。

3 结论

通过对脉冲-旋流气流干燥气固两相流分析及数值模拟的研究，采用欧拉-拉格朗日模型和计算流体力学软件Fluent对脉冲-旋流气流干燥机内部的气固两相流场进行了三维模拟。杨木纤维在脉冲-旋流气流干燥机中的运动状况十分复杂，有很大的随机性，其中在旋流内管口处形成涡流，容易造成返流现象。通过对比添加物料和未添加物料气流相对速度、温度变化得出，加载物料后的气流速度变化明显；并且物料与气流速度有2m/s左右的速度差，有利于传热传质进行。气流速度越大，物料停留时间越短，进料速度的增加延长了物料在干燥机停留时间。模型的数值模拟较真实地反映了气流干燥过程的实际流场及高温气流和木质纤维在干燥管内各参数的变化情况。通过与实验数据对比，二者最大相对误差小于10%，验证使用Fluent气-固两相流模拟方法建立脉冲-旋流气流干燥过程的数学模型是有效的。

[1] PATRO P, PATRO B, MURUGAN S. Prediction of two-phase heat transfer and pressure drop in dilute gas-solid flows: a numerical investigation[J]. Drying Technology,2014,32(10):1167-1178.

[3] 时彤,姜大志,孙俊兰,等.过渡角对脉冲气流干燥器干燥过程影响的研究[J].机械设计与制造,2014(10):206-208.

[4] 张坤媛,于才渊,程茜.脉冲气流干燥管内固体颗粒运动轨迹分析[J].干燥技术与设备,2014(2):32-37.

[5] 水银杰,孙勤,杨阿三,等.旋流干燥器流场模拟研究[J].化学工程,2011,39(3):22-25.

[6] 王锦生,陈程,祝俊宗,等.形状渐变的颗粒与沉降液的相互作用[J].工程热物理学报,2010，31(4):625-628.

[7] LEZCANO C, AMELL A, CADAVID F. Numerical calculation of the recirculation factor in flameless furnaces[J]. Dyna,2013,80:144-151.

[8] MOHAMED M, AMINI M H M, SULAIMAN M A, et al. CFD simulation using wood (Cengal and Meranti) to improve cooling effect for Malaysia green building[J]. ARPN Journal of Engineering and Applied Sciences,2015,10(20):9462-9467.

[9] 时彤,姜大志,孙俊兰,等.基于CFD数值模拟的粉煤灰脉冲气流干燥器干燥性能的研究[J].机械制造,2014,52(8):34-37.