薄壁焊缝SAWH钢管局部屈曲与受弯承载力

刘俊志， 马兆芳， 罗云耀

(1. 北京理工大学珠海学院 数理与土木工程学院， 广东 珠海 519085；2. 中国建筑海外事业部新加坡南洋发展公司， 新加坡 S089315)

薄壁钢管屈曲破坏行为已被研究多年。随着世界经济与工业的飞速发展，对大口径、薄壁化管道的需求不断提高，以“西气东输”为代表的工程对大口径薄壁钢管需求不断加大。与直焊缝钢管相比，螺旋焊缝管因其较低的生产成本、产能，但相对较高强度及结构的稳定性，在大口径钢管应用行业领域已引起高度关注，并将成为新常态。螺旋焊缝管应用尺寸范围大，介于864×10 mm 与2997×25 mm 之间[1]，能高效满足对大口径管道的应用需求。与直焊缝管(纵向焊缝)相比，国内外关于螺旋焊缝管的局部屈曲及弯曲性能研究极其有限，如结构受弯性能、影响因素、局部特征焊缝(如环焊缝、钢带接头焊缝等)对结构力学性能的影响等。

螺旋焊缝管是应用于桩板挡土墙的重要承重构件。在土压力、水压力及黏土压力作用下，竖向荷载通过钢板传递给桩管，钢管主要受到弯曲变形作用，受压弯为主。考虑设计的经济性，具有较高径厚比，大口径钢管截面更加开展、经济，能更好的应用于混凝土钢管复合结构构件[2]。然而随着径厚比的增加，不可避免地，会在弯曲大变形下出现局部失稳，导致钢管桩承载力降低，结构延性变差，最终引起整体结构失稳，甚至造成土体滑坡等工程事故。螺旋焊缝管在受弯曲荷载作用过程中的屈曲性能对结构设计与应用具有重要的理论价值和应用意义。

近年来，越来越多基于“以应变标准设计”代替传统的“以应力标准设计”的研究已在各国逐步开展，我国目前处于落后阶段。目前国内大口径及大径厚比圆钢管的抗弯性能试验研究仅限于直焊缝管，且口径较小。国外钢管局部屈曲的研究仍然局限于比较低的口径，同样局限于传统的直焊缝管。尽管Van[3], Murphey[4], Sorenson[5]等将钢管的径厚比提高至115左右，但局限于直焊缝管与无缝焊管两种工艺的焊管。我国现有GB 50017-2003《钢结构设计规范》[6]只给出了不考虑圆钢管轴压局部屈曲时的临界径厚比控制比值100，未给出关于压弯、纯弯受力的临界径厚比，也未给出圆形钢管的受弯承载力设计计算方法，过于保守粗糙。欧洲规范BS EN 1993-5: 2007《Eurocode 3—Design of Steel Structures—Part 5: Piling》[7]给出了圆钢管受弯过程中的承载力计算及截面分类，然而对初始缺陷的影响给出过量削减，过于保守。

1 “四点受弯”试验

1.1 试验设计与试件制作

试验采用四点受弯机制，中间用铰支座固定钢管并限制中间支座位移，通过控制钢管两端的位移荷载，形成“四点纯弯”。根据API-5L行业标准[8]设计制作了13个螺旋焊缝钢管2个直埋弧焊管，并按照GB/T 2975-1998《钢及钢产品力学性能试验取样位置及试样制备》[9]的规定取样制作标准拉伸试件，钢材的力学性能以及试件具体参数见表1。力臂荷载最大加载3500 kN，钢管受力对称(图1)。以位移控制的荷载通过钢管上的固定钢圈传递给钢管，钢圈具有与钢管相同的厚度。试验发现，左侧钢圈有微小向内缩紧；而右侧钢圈有适量的开口现象。钢圈的变形会引起钢管椭化变形，观察到局部屈曲破坏的位置始终位于离支座处大概4倍直径的距离，局部椭化对结构抗弯性的影响极其有限，故可以忽略。在中间支座处，为避免因支座处的应力集中而引起局部屈曲，通过分别设置钢圈来分散相对集中的荷载，其机制原理见图2，通过螺栓与水平分配梁的连接来传递荷载。分配梁通过铰接的方式与地面支撑结构相连，从而能够实现竖直面最大限度的自由转动。曲率作为衡量钢管变形的参量，也是研究基于应变设计的重要参数[10]。在钢管的纯弯段设置三个局部曲率位移测量计，并在较大范围内设置横跨三个局部曲率位移测量托架的大跨度曲率测量位移计。局部曲率分别定义为曲率1、曲率2、曲率3。大跨度总体曲率定义为总曲率。通过计算钢管抬升过程中四个支座处的位移可以计算出平均曲率，定义为平均曲率(图3)。通过三维激光跟踪仪对钢管表面进行定位，轴向连续测量，环向每隔45°进行数据点的采集；同时用激光跟踪仪对管内部进行测量(图4)。测量初始几何缺陷，包括：壁厚变化、钢管外表面高度变化波动，从而获得螺旋焊缝管的初始缺陷特征。同时在钢管的压拉面设置应变计来测量钢管应变变化并在中性轴处设置应变测量托架记录钢管椭化的情况。比较典型的螺旋焊缝初始缺陷模式测量结果见图5。由图5可知，薄壳结构对初始几何缺陷较为敏感，螺旋焊缝工艺会形成规律性的波浪型初始几何缺陷。对接焊缝特征见图6。从图6可以观察到测量范围内规律性出现峰值，定位螺旋焊缝的位置，并记录钢管加工辊轴造成钢管表面厚度规律性波浪变化的特征位置。

表1试样及具体参数

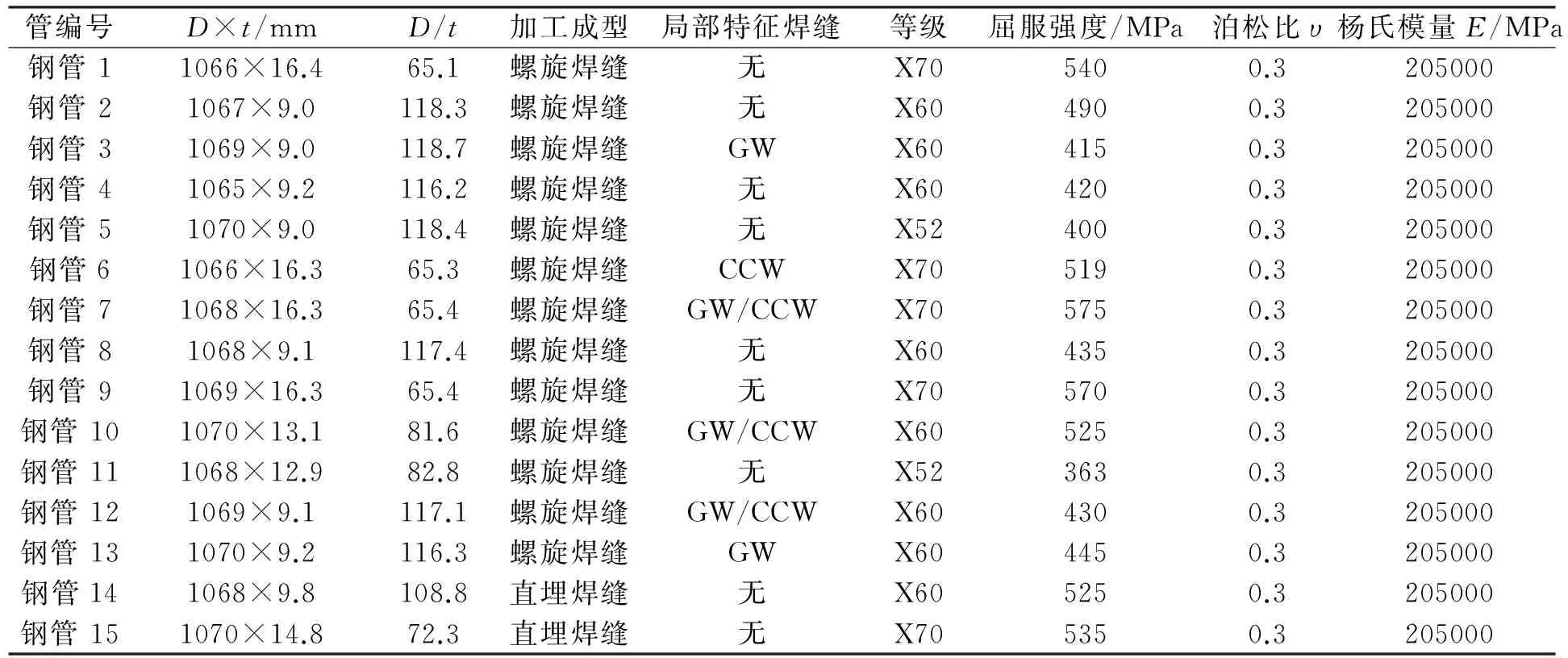
管编号D×t/mmD/t加工成型局部特征焊缝等级屈服强度/MPa泊松比υ杨氏模量E/MPa钢管11066×16.465.1螺旋焊缝无X705400.3205000钢管21067×9.0118.3螺旋焊缝无X604900.3205000钢管31069×9.0118.7螺旋焊缝GWX604150.3205000钢管41065×9.2116.2螺旋焊缝无X604200.3205000钢管51070×9.0118.4螺旋焊缝无X524000.3205000钢管61066×16.365.3螺旋焊缝CCWX705190.3205000钢管71068×16.365.4螺旋焊缝GW/CCWX705750.3205000钢管81068×9.1117.4螺旋焊缝无X604350.3205000钢管91069×16.365.4螺旋焊缝无X705700.3205000钢管101070×13.181.6螺旋焊缝GW/CCWX605250.3205000钢管111068×12.982.8螺旋焊缝无X523630.3205000钢管121069×9.1117.1螺旋焊缝GW/CCWX604300.3205000钢管131070×9.2116.3螺旋焊缝GWX604450.3205000钢管141068×9.8108.8直埋焊缝无X605250.3205000钢管151070×14.872.3直埋焊缝无X705350.3205000

注：GW表示环焊缝；CCW表示钢带对头焊缝；t为壁厚；D为钢管直径，D=(D1+D2)/2，D1为钢管外径，D2为钢管内径

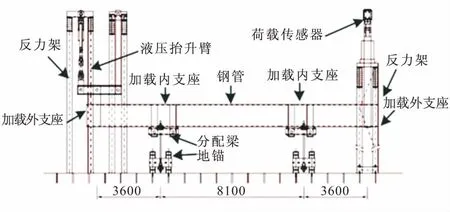
图1 四点受弯试验试验设置/mm

图2 四点受弯试验中间支座的设置

图3 四点受弯试验曲率及椭化测量机制/mm

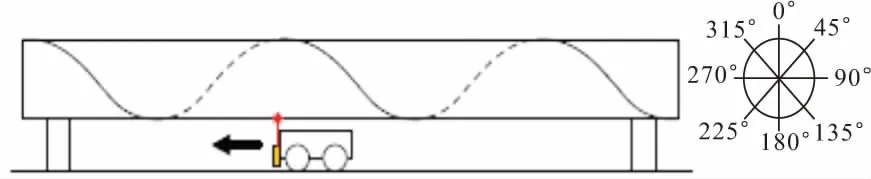
图4 四点受弯试验初始几何缺陷的测量

图5 钢管11局部屈曲位置

图6 钢管3局部屈曲与环形焊缝位置

1.2 加载方案

荷载通过分级加载实现，从弹性阶段传感器为0 kN时开始加载，以0.2 mm/s的速度逐级加载，以每级10 mm开始分步加载直到70 mm(取决于钢管强度及焊缝初始几何缺陷特征)的位移荷载施加完成，开始转换为以5 mm为一级，以相同的速度进行分级加载。局部屈曲发生后，液压力臂继续抬升钢管两端，变形继续，试验总时长大约6 h。试验通过荷载传感器输出的荷载值和位置数据可以得到荷载-位移曲线。静态应变测量系统收集记录应变计以及中性轴处的椭化情况，个别钢管在张拉与压缩试验的对比中表现出包辛格效应，在模拟中应予以注意。

2 试验现象与讨论

试验螺旋焊缝管包含两种不同“局部特征焊缝”，即对接焊缝(环形焊缝)与钢带对头焊缝。这两种“局部特征焊缝”(以下简称“特征焊缝”)对钢管局部屈曲抗弯性能的影响体现在许多方面。钢管1,2,8,11均未包含特征焊缝，局部屈曲发生在波浪模式凹凸缺陷处，远离螺旋焊缝(图5)。钢管3,10,13在特征焊缝处发生屈曲，其中钢管10与13同时具有两种特征焊缝，钢管6在钢带对头焊缝处发生局部屈曲。虽然钢管12同时包含两种不同缺陷，但局部屈曲仍然发生在生产加工引起的规律性凹凸缺陷处(图7)。钢管14与15是直焊缝管SAWL，因其工艺与螺旋焊缝管不同，未出现规律性的表面凹凸变化，也未出现辊轴压制的痕迹，在表面的凹陷缺陷处随机发生局部屈曲。螺旋焊缝初始缺陷不是局部屈曲破坏的决定性因素，也非必要条件。

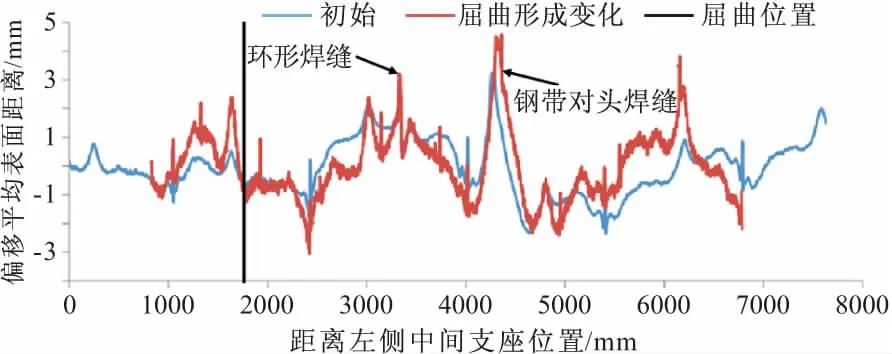
图7 钢管12局部屈曲与局部特征焊缝位置

2.1 边界变化

初始“特征焊缝”将钢管表面区域分隔成具有不同材料特性以及厚度变化的两部分。以含有两种类型“特征缺陷”的钢管10为例，与环形焊缝缺陷相比，钢带对头焊缝分隔的两边区域未出现明显的厚度变化；在环形焊缝的两边区域，厚度发生较大变化，焊缝两侧表面厚度有4%左右的变化，屈服强度有34%的变化；厚度变化引起刚度的变化，引入额外平面内弯矩，导致抵抗力削弱；也从侧面给出理由和预期，局部屈曲会更大概率发生在特征焊缝缺陷处；通常地，屈曲发生在较低强度或厚度较薄的一侧；较低刚度导致曲率的局部集中，从而引起局部屈曲破坏。钢管12的局部屈曲未发生在焊缝缺陷处，对此现象的解释是由于较强的一侧具有较高刚度，从而支撑临近焊缝的另一弱侧，使弱侧出现抗弯刚度加强。

2.2 焊缝强化

焊缝除了作为会引起局部屈曲的初始几何缺陷，还具有某种程度上的强化作用。焊缝的埋弧覆盖层使局部焊缝处厚度增加，抗弯刚度随之增加，从而提高管壁的屈曲抗弯性能。加强情况与加强肋板类似，是钢管12局部屈曲未发生在焊缝缺陷的第二种解释。

2.3 破坏形式与径厚比的关系

由于篇幅限制，只通过对比1、2号钢管进行说明。可以发现，径厚比较低的钢管1(D/t= 65.1)，在钢管进入弹性阶段之后表现出较强的塑性变形能力，即将到达临界弯矩时，弯矩接近全塑性弯矩，局部屈曲破坏出现较均匀厚实的凹凸鼓曲。钢管2(D/t= 118.3)具有较大径厚比，局部屈曲破坏出现严重的压曲褶皱、不规则不均匀凹陷褶皱纹理，构件塑性及延性急剧降低，在到达屈服弯矩之前就已经发生局部屈曲，变形能力差，屈曲破坏对比见图8 。

图8 钢管屈曲抗弯与径厚比关系

2.4 弯矩-曲率关系

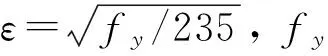
3 有限元模型模拟分析与边界简化

通过ABAQUS建立有限元模型，钢管属于薄壳结构，采用shell壳单元，计算单元采用S4R单元15个截面积分点的辛普森积分[11]。管长16500 mm，为实现钢管在压弯过程中支座处自由椭化变形，在中间支座处用连续分布耦合模拟固定钢管的钢圈，以实现相对位移(图10)。在钢管两端施加位移控制的边界条件，在垂直平面内提拉。通过收敛性分析单元网格尺寸控制在25 mm，考虑材料塑性硬化以及大变形，分析方法采用修正Riks算法，矩阵迭代采用完全Newton-Raphson方法，对模型进行非线性屈曲分析[12]。本文提出的有限元三维模型，要控制好边界条件，满足6个自由度的平衡，避免结构分析不收敛或出现奇异解。钢管在受弯过程中，为避免支座效应(开张或闭合)产生反向作用力(作用机理见图11)引起局部椭化而导致钢管的承载力降低,通过调整支座固定钢圈的方向，最大程度减小钢管椭化影响。在有限元模拟中，如何模拟符合支座实际物理边界条件是需要解决的重点问题(图12)。

图9 钢管延性系数与径厚比、截面长细比的关系

图10 有限元模型以及连续分布耦合的应用

图11 支座效应机制

图12 有限元模型荷载效应机制

通过线性回归分析(图13，14)可以得知有限元数值预测的模拟值能够与试验值高度拟合，该数值模型具有较高准确性，为参数分析提供了高效准确的数值模拟工具。

图13 有限元模拟最大弯矩与试验数据线性回归

图14 有限元模拟临界曲率与实验数据线性回归

4 参数分析

前文利用 ABAQUS 有限元软件建立大径厚比螺旋焊缝钢管的数值模型。在此基础上，本章对大径厚比的螺旋焊缝管进行参数分析，主要考虑初始几何缺陷、径厚比、残余应力以及钢材的屈服强度等参数的影响。

4.1 初始缺陷的影响

初始几何缺陷对螺旋焊缝钢管的受弯及变形性能的影响见图15，16，1号钢管(D/t= 65)，屈服强度fy=540 MPa，钢管外径为1066 mm；2号钢管(D/t=118), 厚度t= 9 mm，屈服强度fy=390 MPa，外径为1067 mm，考虑屈服平台为应变1.5%, 考虑残余应力。图15，16可以看出，钢管的抗弯强度、变形能力对初始缺陷非常敏感。1号钢管具有较强的塑性变形能力。初始缺陷/厚度值小于0.1时，最大弯矩超过95%全塑性弯矩Mp，远大于屈服弯矩。屈服弯矩为名义全塑性弯矩的78.6%左右。其中ky为名义屈服弯矩My对应曲率。定义临界曲率为最大弯矩对应曲率，对于较大初始缺陷，随着缺陷幅值的增加，最大弯矩与应变变形能力显著下降。管壁较薄的2号钢管在初始缺陷变化的所有情况中，最大弯矩承载力全部低于全塑性弯矩的90%。当初始缺陷取最小值(初始缺陷/钢管厚度=0.1)时，最大弯矩仅达到全塑性弯矩的86%；初始缺陷幅值继续增大，最大弯矩远小于全塑性弯矩；从弯矩-曲率图可以看出，管壁较薄的钢管塑性变形能力极其有限。无量纲化曲率随初始几何缺陷的增加以近似对数的关系减小，变形能力对初始缺陷非常敏感(图17)。无量纲化弯矩与初始缺陷的变化近似呈线性关系(图18)。随着初始缺陷的增加，钢管的受弯能力随着初始缺陷的增加而减小，说明钢管的受弯能力与初始几何缺陷有较大的关系，要尽量减小钢管在制作运输安装过程中由加工车间以及人工搬运过程中造成钢管较大的几何缺陷而影响受弯能力。

图15 钢管D/t = 65, X70无量纲化弯矩-曲率关于初始缺陷的M-k图

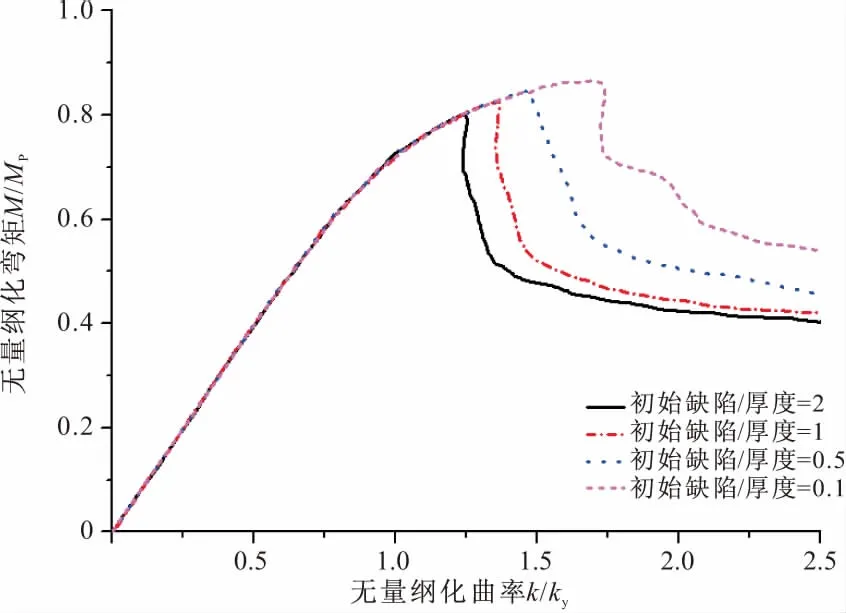
图16 钢管D/t = 118，X60无量纲化弯矩-曲率关于初始缺陷的M-k图

图17 无量纲化曲率与初始缺陷关系曲线

图18 无量纲化弯矩与初始几何缺陷关系曲线

4.2 残余应力的影响

通过比较螺旋焊缝钢管在有、无残余应力两种状态下的弯矩-曲率图(图19，20)发现：当螺旋焊缝管具有残余应力时，其变形曲率大于无残余应力的钢管，在加载初期弹性末端，刚度存在一定程度的局部削弱，造成这样现象的原因可能是，受压区的残余压应力导致了钢管屈服滞后，较晚出现弯曲刚度失效，抗弯抵抗力未出现明显变化。对于螺旋焊缝工艺生产的钢管在某种程度上受益于残余应力。

图19 无量纲化弯矩与无量纲化曲率关于残余应力的M-k图 (D/t = 67, X70)

图20 无量纲化弯矩与无量纲化曲率关于残余应力的M-k图 (D/t = 119, X60)

4.3 径厚比D/t的影响

本节讨论钢管的抗弯及变形能力随径厚比变化的趋势。图21，22是直径为1068 mm，屈服强度为340 Mpa，初始缺陷/厚度=0.036，考虑残余应力的钢管在不同径厚比时的弯矩-曲率图、无量钢化弯矩-曲率图。当径厚比D/t提高时，变形能力及转动能力显著下降；具有相同初始几何缺陷、屈服强度的钢管随着径厚比增加，峰值承载力、跨中挠度、延性、截面变形能力和相对转动能力均降低。从图23可以看出，随着径厚比D/t的增加，钢管变形能力急剧减小，无量纲化曲率与径厚比的关系近似呈幂函数关系。屈服强度较低的钢管下降趋势略大于强度较高的钢管。钢管抗弯性能随着径厚比的增加而减小(图24)。无量纲化弯矩与径厚比的关系近似为线性关系。随着径厚比增加，钢管跨中受弯能力减小。在生产中，可以根据设计及需要通过控制径厚比这一变量来满足强度及变形的需要。

图21 弯矩-曲率关系曲线

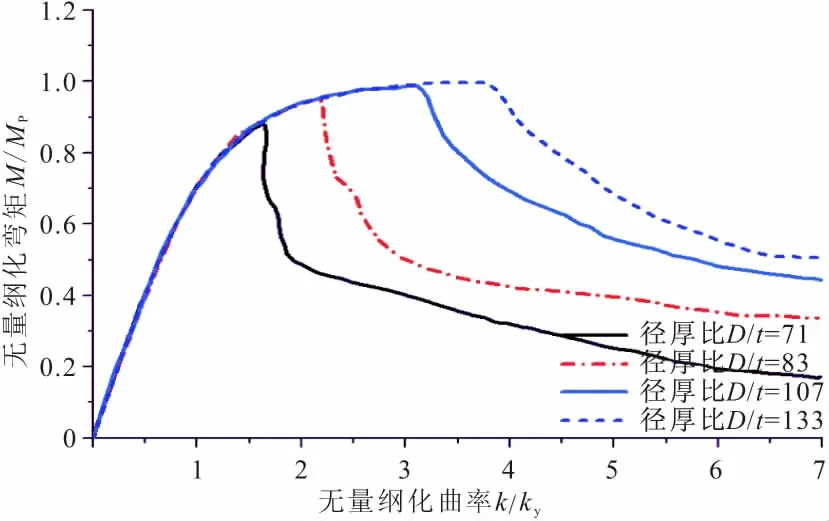
图22 无量纲化弯矩-曲率关系曲线

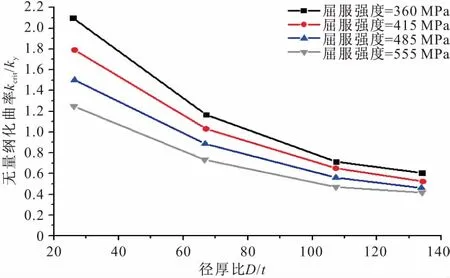
图23 无量纲曲率与径厚比关系曲线

图24 无量纲化弯矩与径厚比关系曲线

4.4 屈曲破坏形式与径厚比D/t的关系

超大口径螺旋焊缝钢管SAWH以及直焊缝钢管SAWL的局部屈曲破坏形式与钢管的径厚比有较大的关系。

有限元数值模拟钢管局部屈曲破坏形式 (图25，26)。四根钢管具有相同屈服强度、口径、初始几何缺陷，径厚比分别为65， 66， 116， 118。具有较小径厚比的钢管，屈曲破坏模式呈向内凹陷破坏或鼓曲破坏，由钢管中央区域一部分较宽的主屈曲及钢管受弯平面内主屈曲两端的副屈曲组成(图26a，26b)，具有较好的塑性及较好的变形能力，跨中截面最大弯矩接近全塑性弯矩，局部屈曲限制了钢管受弯形变的进一步变形能力，未能在跨中形成塑性铰。对于具有较高径厚比的钢管，局部屈曲的破坏模式呈向内的凹陷褶皱模式，破坏较锐利，局部屈曲破坏波长较短，除了两边的副屈曲，还有额外的第三屈曲区域(图26c，26d)，变形能力较差。当跨中截面出现局部弯矩集中，应力高度集中，受弯到最大极限时，受局部屈曲破坏影响，承载力急剧下降，体现出较差的变形能力、延性。有限元的破坏模式与试验屈曲破坏良好的吻合。

图25 屈曲破坏模式(水平投影)

图26 屈曲破坏模式(轴测投影)

4.5 材料屈服强度fy的影响

通过控制初始几何缺陷变量(分别为0.01，0.05，0.1，0.15，0.2五个初始缺陷幅值)，无量纲化曲率与钢管屈服强度的关系曲线见图27。可以看出，钢管变形能力随屈服强度的增加而降低，近似为幂函数的关系。对于较低径厚比的厚钢管影响较大。

图27 无量纲化曲率与屈服强度关系曲线

无量纲化弯矩与屈服强度的关系曲线见图28，从图28可知，钢管抗弯变形能力随屈服强度的增加而有所降低，无量纲化弯矩与钢材屈服强度的关系近似为线性关系。

图28 无量纲化弯矩与屈服强度关系曲线

5 结 论

本文介绍了超大口径，大径厚比的螺旋焊缝及长直焊缝钢管的四点受弯试验方案及加载机制，对13根大直径螺旋焊缝管、2根直焊缝管进行了研究。讨论了边界条件、几何参数等对试验结果的影响。同时介绍了有限元模型的建立与工作机制，通过借助有限元软件建立数值模型分析15根钢管来研究材料、几何等参数对钢管抗弯性能的影响。得出以下结论：

(1)所有钢管都是由局部屈曲破坏引起的失稳。通过参数分析，钢管的最大弯矩承载力与径厚比有极大的关系。管壁较薄、径厚比较高的钢管屈曲破坏更加突然，塑性变形能力有限，最大抗弯承载力略高于屈服弯矩，远低于全塑性弯矩。相反地，径厚比较低，管壁较厚的钢管具有极强的塑性变形能力，局部屈曲破坏比较平缓，有渐进的过程。

(2)钢管变形能力以及弯矩承载力与初始几何缺陷有极大的关系。随着初始几何缺陷的增加，钢管变形曲率与抗弯承载力迅速降低。降低幅度与径厚比有较大关系，对于径厚比较大的钢管，在生产、预制及应用过程中要加强对初始几何缺陷的控制。

(3)通过对比，有残余应力的钢管变形能力优于无残余应力的钢管。在螺旋焊缝管的屈曲破坏中，屈曲破坏位置与预期判断孑然相反，局部屈曲并未发生在边界条件发生变化的螺旋焊缝处，说明螺旋焊缝对钢管局部屈曲破坏的位置并没有决定性的作用及影响，局部抗弯承载力与直焊缝管表现无较大差别。

(4)钢管材料性能对钢管的抗弯承载力有较大的影响。钢管的均一化曲率与均一化弯矩随着屈服强度的提高而降低。屈服强度越高的钢管，最大跨中弯矩也越大，但临界曲率却越小。

[1] ArcelorMittal. Spirally Welded Steel Pipes: Netherlands[P]. 2010.

[2] 郭兰慧, 牛 奔, 杨诗君. 薄壁及加劲圆钢管的抗弯性能研究[J]. 土木工程学报, 2013, 46(8):19-27.

[3] van Douwen A A, Gresnigt A M, Stark J W B. Plastic Design of Buried Steel Pipelines for Transport of Oil, Gas or Water, Verified by Tests on Scale Models[R]. Netherlands: TNO-IBC, 1974.

[4] Murphey C E, Langner C G. Ultimate Pipe Strength under Bending, Collapse and Fatigue[R]. Netherlands: Shell Development Company, 1975.

[5] Sorenson J, Mesloh R E, Winegardner R. Buckling Strength of Offshore Pipelines[R]. Netherlands: Batelle Report to Offshore Pipeline Group, 1970.

[6] GB 50017-2003, 钢结构设计规范[S] .

[7] BS EN 1993-5: 2007, Eurocode 3—Design of Steel Structures—Part 5: Piling[S].

[8] ANSI/AISC 360-10, Specification for Structural Steel Buildings, AISC [S].

[9] GB/T 2975-1998, 钢及钢产品力学性能试验取样位置及试样制备[S].

[10] Bransby M F, Davies M C R, Nahas A El. Centrifuge modeling of normal fault-foundation interaction[J]. Bulletin of Earthquake Engineering, 2008, 6(4): 585-605

[11] 薛嘉行, 姜开厚, 杨嘉陵, 等. 弹-塑性圆管受纯弯载荷作用的实验研究 [J]. 应用力学学报, 2000, 17(4): 50-57.

[12] Heedo Yun, Stelios Kyriakides. On the beam and shell modes of buckling of buried pipelines[J]. Soil Dynamics and Earthquake Engineering, 1990, 9(4): 179-193.