非线性无量纲化插值分类的一种新方法

廖志高，詹 敏，徐玖平

(1.广西科技大学 管理学院，广西 柳州 545006；2.四川大学 商学院，成都 610064）

0 引言

无量纲化方法是将原有单位、属性值等不同的指标数据进行规范化，便于不同指标间数据相互进行比较。任一种线性无量纲化方法其变换函数均可表示为：ξij=f(Xij)=kXij+b，i=1，2，...，n的形式，其中k、b为待定系数。原始指标数据经函数变换后计算得规范化值，其规范化值与原始数据之间的关系始终都是线性关系。虽然线性无量纲化方法使用比较方便，研究成果也相对较多，但其仍存在先天局限性。因为在实际生活中并非所有的规范化值与原始指标之间的关系均是线性关系的，线性关系只是无量纲化方法中的一种特殊形式，其中更多的则是非线性关系，如“边际效用递减”规律等[1]。在无量纲化过程中全部用线性关系的无量纲化方法对原始指标进行无量纲化处理，那所得到的综合评价结果很难说是客观、科学的。且当指标数据中出现异常极值点时，由于异常点对线性无量纲化数据的稳定性产生严重影响，当增加或减少某个异常点后，无量纲化结果可能会发生很大变化，这时就需要对异常点进行判断识别甚至是修正，而不是简单的直接使用线性无量纲化方法。所以在无量纲化处理过程中对异常点的考虑及根据实际情况采用非线性无量纲化方法进行处理非常必要。而目前对于异常点及非线性无量纲化的处理仍然还非常少，因此进行此类研究已变得非常必要。

1 非线性无量纲化方法及异常点的处理

1.1 非线性无量纲化方法

与常用的线性无量纲化方法不同，非线性无量纲化方法的特点是其变换函数的变化率不是恒定的。即对于同一指标，其不同指标数据的斜率是不恒定的，因此指标值的变化对评价值的影响是不等比例的。现有的非线性无量纲化方法主要有如下几种：效用函数型、折线型无量纲化处理、基于曲线拟合的无量纲化方法处理和强“奖优罚劣”算子处理等[2～7]。

1.1.1 效用函数型

戴文战、邹立华、汪建章等(2000)所写《一种基于奖优罚劣原则的多阶段多目标决策模型》一文，其中提出了一种新颖的效用函数，并据此将具有不同量纲、不同物理意义、不同指标类型的决策矩阵归一化转换到相应的效用矩阵，该效用函数以指标的平均值为参考点，突出了“奖优罚劣”原则，提高了分辨精度，物理概念更加清晰，并应用实例说明了该方法的合理可行性。同时为转换系数，该效用函数为由于是一条S型曲线，bij反映了原始数据偏离平均值的关系，当原始数据大于4倍以上平均值或小于-4倍平均值时，效用函数接近“饱和”，这样处理防止了因某些分指标出现特大或特小等异常点左右整个综合评价的取值，其本身对“异常点”有一定的削弱作用[2]。

本文对其效用函数：y=(1-e-x)/(1+e-x)，进行分析试图找出其对指标数据的影响。我们对其进行求导，分析其不同指标值时的变化率。

易知0＜y'＜1恒成立，因此其效用函数只对x进行缩小而无放大作用。且在x=0附近其斜率最大，随着|x|＞0，其斜率越来越小直至趋近于0。其主要适用于数据在平均值附近比较集中的数据。

但该文的不足之处是在计算转换系数时没有考虑平均值为0以及区间上界或下界为0的情形，此时转换系数计算公式分母为0分式无意义需要作特殊考虑。解决方案：对于平均值为0的情形，需要对数据进行具体分析，若数据分布均匀且数值相对较小可不进行转换，此时；当区间上界为0或下界为0时，需要对数据进行具体分析，可利用先进行简化处理等。

1.1.2 折线无量纲化方法

蔡辉、丁昌慧（2003）在《综合效益评价中数据的非直线化无量纲化方法》一文中，考虑了转折点，即每条线段都是直线，但是它们的直线方程是不一样的，主要表现为斜率的不相同并连接在一起。其适用条件为指标变动不均衡，或在指标的不同值域内，实现指标值的综合效益评价难易程度不同。此时宜采用非线性无量纲化方法。同时其还指出模糊数学中的隶属函数也是分段函数，用这种方法处理实质上也属于指标的折线型无量纲化方法[3]。

该种方法其难点在于如何确定转折点，这需要根据实际情况做具体分析，同时对于某些情况转折点位置不明确或存在多个转折点时更需详细考虑。并且很多时候数据间不是突然的质变而是缓慢变化的，此时没有明确的转折点但其斜率的变化还是存在，此时则需要进行非线性无量纲化，而折线型无量纲化已不再适用。但非线性无量纲化方法相对于纯线性无量纲化方法而言是一种进步。

1.1.3 基于曲线拟合的无量纲化方法处理

温洪涛，任传鹏（2010）在《企业绩效评价指标的无量纲化方法的改进》一文中，运用曲线拟合的无量纲化方法从各类指标的核心特点出发，分别制定了各类指标的归一化方法，使处理后的数据更能保留原始信息，最大限度地减少了信息损失和信息失真。同时经变换后得到的规范化值向两端聚集，即“优者更优”、“劣者更劣”。从而起到了“激励先进，惩罚落后”的效果[4]。

需要指出的是，其曲线拟合均是运用指数函数拟合且底数均为e，其拟合精度有一定的局限性适用范围非常有限。

1.1.4 强“奖优罚劣”算子

宋捷、党耀国、王正新（2010）在《基于强“奖优罚劣”算子的多指标灰靶决策模型》一文中，其提出强“奖优罚劣”算子，在传统“奖优罚劣”算子赋值范围扩展到负值基础上，通过使用非线性变换将平均值水平附近的“平庸”指标赋值的绝对值减小，这样将各指标赋值范围进一步扩大，以便于决策者进行决策分析[5]。

根据常用函数类型及我们可将以上几种非线性无量纲化方法分为以下三种类型。

通过对以上四种非线性无量纲化方法进行分析可知，非线性无量纲化方法其变换函数的变化率不是固定的，即变换函数的斜率k或者称之为原函数的导数其是变化的。对于正向化指标k＞0，规范化数据随着原始指标数据的增长而单调递增。变换函数具有如下三个特点：(1)当k＞1时，变换函数表现为对变换数据进行放大；(2)当0＜k＜1时，变换函数表现为对变换数据进行缩小；(3)当k=1时，变换数据既不被放大也不被缩小。对于区间型指标和逆向化指标均需要先正向化然后再进行函数变换。

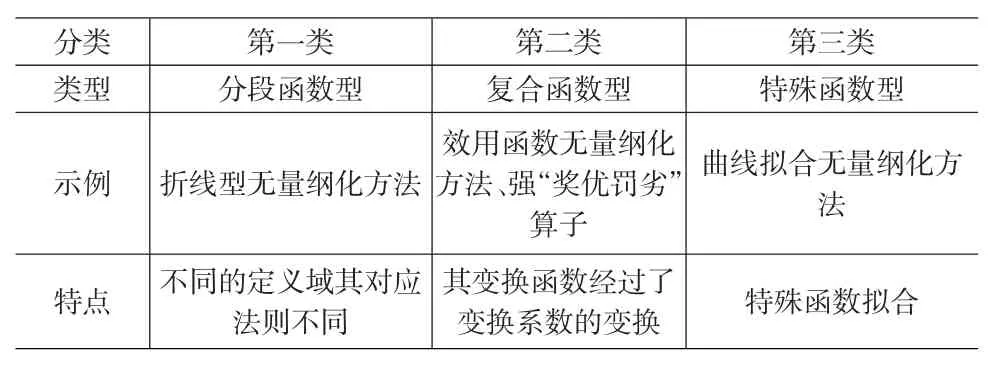
表1 非线性函数分类

1.2 异常点处理方法

关于异常点，不同的定义规则对其定义不同。但一般均有如下表现：第一，除该点或该几个点之外的其他数据过分集中，并且明显偏低或偏高，因而在评价过程中降低了被评价对象的信息量使得较集中的数据识别度较低；第二，这类点的存在使得预处理后的数据极不稳定，增加或减少该异常点对于指标预处理的结论影响很大。对于异常点的处理，一方面希望异常点越少越好，尽量保持评价值的原貌；另一方面则希望挑出较多的异常值，使得评价结果更加准确。在实际问题处理过程中，有时还需要对异常点进行特殊考虑加以分析找出其存在的原因并做出相关合理解释。

1.2.1 上下异常点处理

郭亚军、易平涛(2008)在《线性无量纲化方法的性质分析》一文中关于异常点的影响进行了研究。其定义了上异常点和下异常点，并提出了保留信息率、改进度和协调值等概念，通过对异常点的识别和循环调整来修正异常点改进无量纲化方法。此为人为直接识别之外较为规范的“异常点的数值确定方法”。同时还指出，非线性无量纲化方法中如半正态分布、半哥西分布等方法本身对“异常点”有一定的削弱作用[6]。

1.2.2 基于正态区间估计的改进型无量纲化方法处理

何乃强、惠晓斌、周漩（2012）在《基于正态区间估计的改进型无量纲化方法》一文中，提出了一种基于正态区间估计的改进型无量纲化方法，利用正态区间估计的方法给出异常评价值的定义规则和处理规则，按照规则对评价值异常点进行辨识和修正，采用标准化方法对评价值进行无量纲化，提高评价值之间的区分度，经算例分析表明，该方法可行有效[7]。

从已有的关于异常点的处理方法可知，主要是定义规则找出异常点并进行修正。最终使评价结果更加真实明朗便于决策。而对于某些非线性函数则对异常点有减弱的作用。

2 基于反三角函数的非线性无量纲化方法

2.1 反三角函数简介

图1 四种反角函数基本图象

图1为反正弦函数、反余弦函数、反正切函数和反余切函数的基本图象，其具体表达式定义域、值域导数、单调性和奇偶性如表2所示。

表2 反三角函数简介

从表2可知，反正弦函数和反余弦函数的导数的绝对值均大于等于1，其对x有放大作用，而反正切函数和反余切函数起导数的绝对值均小于等于1，其对x有缩小作用。将反余弦函数和反余切函数的图象向下平移，使各函数的值域相同。从而可以利用其性质，将其作为一种无量纲化方法进行无量纲化。

2.2 基于反三角函数的非线性无量纲化方法

设有m个样本，每个样本都有n个指标，则第i个样本的第j个指标的指标值为Xij，其中i=1,2,…,m;j=1,2,…,n。

2.2.1 反正弦函数和反余弦函数的无量纲化方法。

用表示m个样本中第j个指标的均值，则

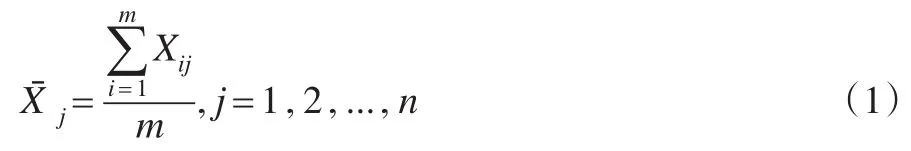
转换系数为Zij则

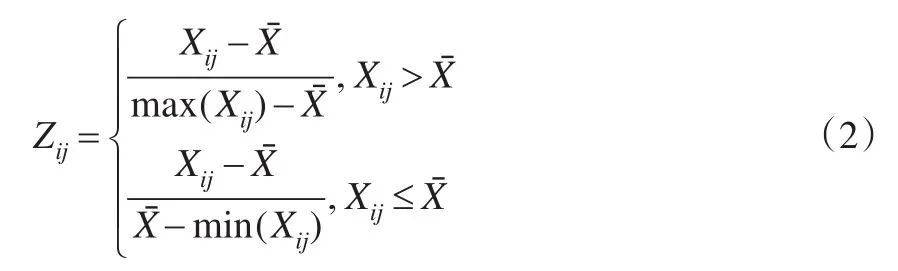
若Pj为效益型指标，则变换函数为：

若Pj为成本型指标，则变换函数为：

若Pj为区间型指标Xij∈[A，B]（包括固定型，此时A=B），则

当Xij＜A时，其转换系数Zij为：

变换函数：

当Xij＞B时，其转换系数Zij为：

当Xij∈[A，B]时，则其转换系数Zij=1，变换函数：

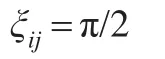
2.2.2 反正切函数和反余切函数的非线性无量纲化方法

若Pj为效益型指标，则ξij=arctanw*Zij;

若Pj为成本型指标，则ξij=arccotw*Zij-π/2;

若Pj为区间型指标uij∈[A，B]（包括固定型，此时A=B），则

当Xij＜A，其转换系数Zij为：

当Xij＞B，其转换系数Zij为：

当Xij∈[A，B]，则ξij=π/2。

其中w的取值，可以根据不同的实际需要进行伸缩变换调整，以便更好的进行无量纲化运算。

表3 各特殊点的取值

根据百分比可知，反正切函数和反余切函数可以有效减弱异常点的影响。一般来说，当现象总体中有异常点（极大或极小值时），宜计算和应用中位数和众数，因为它们可以消除极端值的影响，比算术平均值更能代表总体的一般水平。

无论哪一种统计指标，都有它自身的优势，也有局限性。总量指标能够反映事物发展的总规模和总水平，却不易看清事物差别的程度；相对指标反映了现象之间的数量对比关系和差异程度，却又将现象的具体规模和水平抽象化了。因此，将相对指标和总量指标相结合起来使用，才能克服认识上的片面性，达到对客观事物全面正确的认识。

3 几种简单插值分类方法

样本数据一般可分为离散型和连续型两类。对于离散型数据在数理统计中我们一般使用基本统计量包括：平均数、众数、中位数、极差、方差、标准等来描述数据的特征；而对于连续型数据，我们一般将其作为函数处理，包括连续函数、分段函数，以及特殊的区间数等，此时我们常计算其特殊点如最大值、最小值、极值点、拐点、端点值等来更好的描述数据。当然在对原始数据进行数据处理的过程中，我们还可根据实际需求进行一些特殊处理。基于各统计量及特殊点思想，以及上述综合评价方法的不足，本文提出一种基于插值分类的综合评价方法，在此插值分类一般分为：算术平均分类法、极差分类法、几何平均分类法以及根据其他特殊需求而进行的特殊点分类法等。

方法步骤为：

首先，将逆向指标和适度指标的原始数据进行正向化；

其次，根据数据特点选择插值分类方法进行插值分类，并对分类数据进行无量纲化；

最后，利用综合模型进行综合评价。

（1）算术平均分类法

先将样本数据中单个指标的正向化数值进行降序排列，然后进行求和，最后分别找出其最小值、最大值，再计算其算术平均值及所需要的分类插值。

对于第j个指标，共有m个样本则，

（2）几何平均分类法

（3）极差分类法

若将第j个指标的最大值与最小值作差得极差dj=max{Xij}-min{Xij}，利用公式ξj=min{Xij}+q*dj/n，q＜n，q、n∈z+即得第j个指标的各分类点。例如，当n=3,q=1时则计算出的ξj值为第j个指标的1/3极差分类点，当n=3,q=2时，则计算出来的ξj值为第j个指标的为2/3极差分类点。

（4）特殊点分类法

根据实际需求插值，例如老师在看某班50名学生考试成绩时还可取每科排序前10位的平均值作为成绩优秀的标准，前25位的平均值作为成绩良好的标准等，也可以取特定的某一值作为标准插值求综合分类排名。

将各不同指标的相同分类点组成一个样本即可得一个分类样本。将不同分类点组成的多个分类样本进行评价即可进行插值分类。

例如，将处于先进算术平均数样本评价值与最大值样本评价值间的评价值分为第一类；将处于算术平均数样本评价值与先进平均数样本平均值间的评价值分为第二类；以此类推可分为第三类、第四类。

4 案例分析

以文献[4]中的应用实例作为本文的案例，利用反正弦函数和反余弦函数的无量纲化方法进行数据分析处理，并采用极差分类法进行插值分类，并用多指标靶决策模型进行评价。由于靶决策模型在文献[4]中有叙述在此不作熬述。

为开发新产品，拟定了五个投资方案 S1、S2、S3、S4、S5。样本插入值分别为最大值样本S6、3/4极差样本S7、1/2极差样本S8、1/4极差样本S9、最小值样本S10，见表4。其中，期望净现值和风险盈利值为正向化指标，投资额和风险损失值为逆向指标。

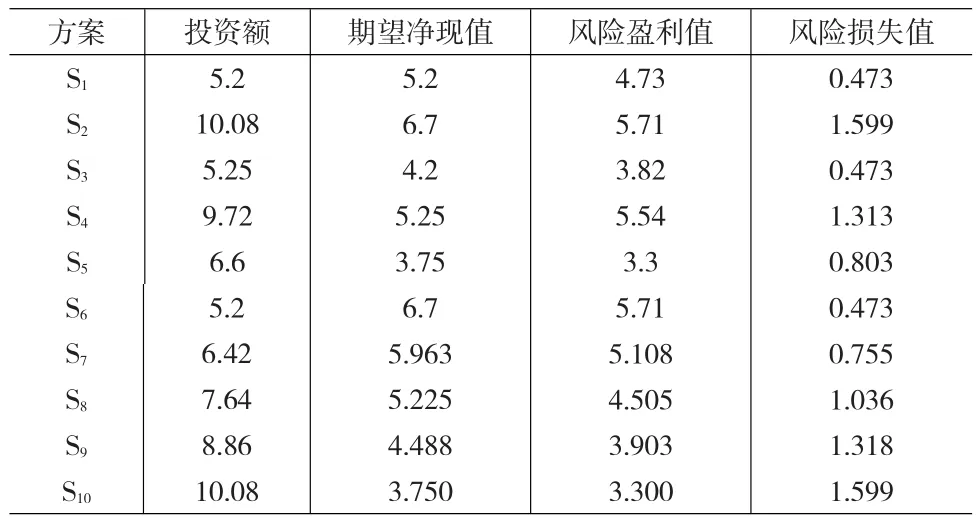
表4 各方案的效果样本值及插入值

表5 经反正弦函数和反余弦函数无量纲化后决策数据

表6 数据处理结果

由Si的从小到大进行排列可知：S1＞S3＞S4＞S5＞S2。

且通过分类可知：S6处于第一类优于3/4极差样本；S3处于第二类在3/4极差样本和1/2极差样本之间；S4处于第三类，其低于1/2极差样本但高于1/4极差样本；而S5和S2最差，处于1/4极差样本以下。

5 结语

通过对已有线性无量纲化方法的研究，及对异常点的分析，指出线性无量纲化方法的不足，同时结合现有非线性无量纲化方法，归纳出非线性无量纲化方法的三种类型并说明了其三个特点。同时提出了一种新的非线性无量纲化方法，即基于反三角函数的无量纲化方法，并且还提出一种插值分类方法，在综合评价的同时还进行了分类集群定位，对此均进行了案例论证。

[1]谢铭杰,韩兆洲.线性无量纲化方法的局限性[J].统计与决策,2005,（3）

[2]戴文战,邹立华,汪建章等.一种基于奖优罚劣原则的多阶段多目标决策模型[J].系统工程理论与实践,2000,（6）.

[3]蔡辉,丁昌慧.综合效益评价中数据的非直线化无量纲化方法[J].中国医院统计,2003,10(1).

[4]宋捷,党耀国,王正新.基于强”奖优罚劣”算子的多指标灰靶决策模型[J].系统工程与电子技术,2010,（6）.

[5]温洪涛,任传鹏.企业绩效评价指标的无量纲化方法的改进[J].经济问题,2011,（6）.

[6]郭亚军,易平涛.线性无量纲化方法的性质分析[J].统计研究,2008,（2）.

[7]何乃强,惠晓滨,周漩.基于正态区间估计的改进型无量纲化方法[J].计算机工程与应用,2012,48(5).

[8]党耀国,刘国峰,王建平等.多指标加权灰靶的决策模型[J].统计与决策,2004,（3）.