基于IFS与TOPSIS的城市基础设施PPP项目融资风险评价

赵 辉， 屈微璐， 邱玮婷， 董 骅

(青岛理工大学 管理学院， 山东 青岛 266520)

随着我国城镇化进程的不断推进，对于城市基础设施的要求也越来越高。而城市基础设施的建设对于资金量的需求是巨大的，为了解决这一问题，十八届三中全会曾提出允许社会资本通过特许经营等方式参与城市基础设施投资与运营，在这种模式下城市基础设施项目的投融资结构较为繁琐，融资风险因素较多，具有阶段性、复杂性、风险周期长以及参与方众多等特点[1～3]，其涉及项目的工期、成本、质量以及运营收益等多个方面，风险发生的概率以及造成的损失大小具有很大的不确定性[3～6]，融资风险影响结果较为严重，使得融资风险对于项目的顺利与否起到了举足轻重的作用。因此对PPP(Public-Private-Partnership)模式下的城市基础设施项目进行融资风险评价研究对我国当前城市基础设施的建设有着非常重要的现实意义。

对于PPP模式下城市基础设施项目融资风险的评价，国内外均进行了相应的研究分析。国外方面，Fischer等[7]对PPP项目的风险管理建立了比较完整的体系；Xu Yelin等[8]运用模糊评估方法建立了PPP项目的融资风险评价模型；Grimsey等[9]对基础设施应用PPP模式的风险作出了研究。国内方面，张萍等[10]运用模糊综合评价方法对城市基础设施PPP模式下融资风险的三个特征进行了分析；莫吕群等[11]运用层次分析法并结合实际案例甄别出了城市基础设施PPP项目融资中的重要风险影响因素；孙荣霞[12]利用霍尔三维结构从三个维度分别对基础设施PPP项目的融资风险进行了研究；李公祥等[13]提出了针对不同类型的城市基础设施项目应选择不同结构的PPP模式；陈波等[14]通过建立线性规划模型提出了PPP项目融资风险分配的新方法；王雪青等[15]运用模糊数学方法对高速公路PPP项目的融资风险进行了分析。现有的关于融资风险的定性研究大都集中在较为广泛的PPP项目上，而针对PPP模式下城市基础设施项目的融资风险大多为定性研究。本文总结了各文献所提出的融资风险因素，针对复杂的风险指标体系，为了改善以往文献中对于指标评价准确性的缺失问题，利用直觉模糊集来表示风险因素的模糊性与不确定性，构建评价矩阵，以便更加充分地获得评价专家与评价指标的信息，并且将直觉模糊集与逼近理想解的排序法(Technique for Order Preference by Similarity to an Ideal Solution，TOPSIS)结合起来，试图构建城市基础设施PPP项目融资风险评价模型，对PPP模式下城市基础设施项目的融资风险进行客观全面的评价，以保证我国城市基础设施的稳定发展。

1 城市基础设施PPP项目融资风险评价指标体系

PPP项目融资是一个专业性强、涉及范围广且较为复杂的系统过程，从立项一直到投入使用过程中，参与方众多，融资结构相对复杂，将PPP模式应用到城市基础设施中是一大创新性挑战。PPP项目融资本身具有的风险性，结合城市基础设施固有的长期性以及公众性，极易可能产生未预料到的后果，若想避免风险的发生，首先需要了解其形成机制(图1)，来自于内外部的风险影响因素从不同的方面构成了该项目的风险事件，以致于造成诸如成本增加、工期延长、质量下降以及收益变化等后果。

图1 项目融资风险形成机制

根据PPP项目融资的风险形成机制，每个项目由于其所处的内部、外部环境不同，造成了各种不可预估的融资风险。本文主要通过总结国内外文献对于基础设施PPP项目融资风险的识别研究[5～12]，以我国城市基础设施所独有的特点为基础，结合全面性及科学性、适用性与可量化以及系统性和逻辑性原则，从多个角度进行分析建立了具有动态性以及全面性的风险评价指标体系，如表1所示。

表1 城市基础设施PPP项目融资风险

2 基于IFS与TOPSIS的城市基础设施PPP项目融资风险评价

由表1可知，PPP模式下的城市基础设施项目在融资风险方面有众多的影响因素，且这些指标涵盖范围较为广泛。在融资风险评价中，由于各专家在专业方面的局限性，若仅仅依靠专家对于影响指标的主观判断则缺乏一定的准确性，并且在方案的选择过程中也具有较大的主观性。对此，Atanassov[16]曾提出了直觉模糊集的思想可在一定程度上保证指标参数确定的完整性；Hwang等[17]提出的TOPSIS法可根据综合评价指数对方案进行客观排序以选择最优方案。本文通过引入直觉模糊集(Intuitionistic Fuzzy Sets，IFS)来表示各融资风险指标对于该PPP项目影响的隶属度与非隶属度，再利用得分函数建立求解指标最优权重的线性模型，结合TOPSIS决策方法得出综合评价指数，在一定程度上避免了主观误差，能够从更加全面的角度对评价体系作出分析。具体的基于IFS与TOPSIS的城市基础设施PPP项目融资风险评价模型框架如图2所示。

图2 城市基础设施PPP项目融资风险评价模型

2.1 IFS与TOPSIS的基本理论

2.1.1直觉模糊集(IFS)

自美国控制论专家Zadeh[18]于1965年提出模糊集理论以来，该理论便被逐渐应用到了国民经济的各个领域之中。模糊集的核心思想是把取值仅为1或0的特征函数扩展到可在单位闭区间[0，1]中任意取值的隶属函数，而该隶属函数表达信息较为单一。之后保加利亚学者Atanassov[16]便对Zadeh的模糊集进行了拓展，提出了直觉模糊集的概念，该理论同时考虑到了隶属度、非隶属度和犹豫度这三个方面的信息，很大程度上缓解了模糊集中指标参数确定的问题。

定义1[19]：对于一个论域X，设X={x1,x2,…,xn}为非空有限集，则将A={〈x,μA(x),νA(x)〉|x∈X}定义为论域X上的一个直觉模糊集，其中μA(x)和νA(x)称为A的隶属度函数和非隶属度函数，μA(x)∈(0,1),νA(x)∈(0,1)则各自代表了元素x属于A的隶属度和非隶属度，并且对于x∈X同时满足条件0≤μA(x)+νA(x)≤1。

定义2[19]：对于论域X上的任一直觉模糊集，称πA(x)=1-μA(x)-νA(x),x∈X为元素x属于集合A的犹豫度或不确定度，即对于元素x是否属于集合A的犹豫程度的一种度量，易知0≤πA(x)≤1,x∈X，且πA(x)越小，元素x相对于集合A的未知信息就越少，则决策者对于自己做出的判断就越肯定。

2.1.2TOPSIS法

在理想解以及权重已知的情况下，运用TOPSIS算子来解决多属性决策问题可以保证方案选择的客观性。Hwang等[17]于1981年提出的TOPSIS法，又称为逼近理想解的排序方法，它通过计算方案集中各方案与理想解和负理想解的距离给方案集中各方案进行排序，即靠近理想解又远离负理想解的方案为最佳方案。具体思路如图3所示。图3表示两个属性的决策问题，f1和f2为加权的规范化属性，方案集X中的六个方案x1～x6的加权规范属性值如图中位置所示，x+和x-分别表示理想解与负理想解，其中x4,x5到理想解的距离最近且相同，x4距离负理想解比x5远，由此可判断方案优劣。

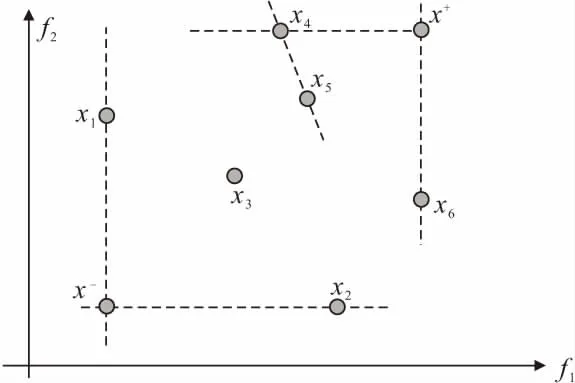
图3 理想解与负理想解示意

2.2 基于IFS与TOPSIS的城市基础设施PPP项目融资风险评价具体步骤

(1)构建直觉模糊集评价矩阵

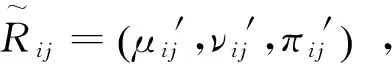
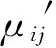
(2)求解最优权重

式中：aij=(μij,νij)；S(aij)=(μij-νij)+(μij-νij)πij=(μij-νij)(1+πij)。

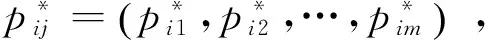
(3)计算加权直觉模糊集矩阵Q

(4)计算各项目到正负理想解的距离

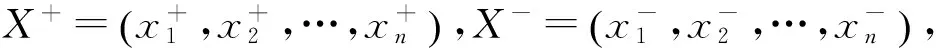
项目Ai到直觉模糊集正负理想解的距离分别为：

(5)计算各项目与正负理想方案的贴近度

3 实证应用

为了缓解城市用地紧张，交通拥堵的现状，某人口大省计划引进PPP模式修建5处公共地下车库，为了有效地分析这5处城市公共地下车库的融资风险状况，现运用IFS与TOPSIS相结合的方法对这5处地下车库PPP项目融资风险进行评价。由于城市公共地下车库对于开发规模、地区选址以及服务半径等都有着较高的要求[20,21]，本文请专职于城市基础设施、PPP项目的投融资专家、项目经理以及政府官员等10人组成专家组，采用直觉模糊数的形式对表1所示的16个风险指标进行打分。

(1)直觉模糊集评价矩阵P如下：

(2)确定各指标组合权重向量

借助MATLAB工具，利用上述线性模型，可以获得各指标的权重：

集成后的权重为：w′T= (0.036,0.107,0.042,0.103,0.049,0.116,0.042,0.030,0.030,0.130,0.057,0.054,0.061,0.027,0.090,0.026)

直觉模糊形式下的权重为：

(3)计算加权直觉模糊评价矩阵Q

(4)构造直觉模糊集正理想方案与负理想方案(表2)，计算各项目的综合评价指数(表3)。

表2 直觉模糊集的正理想解和负理想解

表3 各项目到理想解的距离及其综合评价指数

由表3可知，各项目的优劣次序：A3≻A2≻A1≻A5≻A4,即第三处地下车库A3融资风险相对较小，比较适合该城市的规划发展。

4 结 语

本文在基于IFS与TOPSIS法的基础上，对于PPP模式下的城市基础设施融资风险评价的研究主要解决了以下3个问题：

(1)客观性。由于PPP模式下的城市基础设施项目融资风险的评价指标涉及多个学科领域，本文采用了直觉模糊集的形式来构建评价矩阵，然后用TOPSIS法进行排序，避免了专家由于专业知识限制而产生的评价主观性。

(2)全面性。本文在遴选评价指标构建评价体系时，对现有的关于融资风险评价的文献做了大量总结，并结合PPP模式下城市基础设施项目融资的特点，从多个方面对评价指标进行了筛选。

(3)适用性。本文创造了一种在模糊语言环境下，运用TOPSIS算子对设施项目进行排序的方法，并通过实证研究更好地说明了该评价方法对于PPP模式下城市基础设施项目融资风险评价的适用性。

“客观性”“全面性”和“适用性”的实现，使得基于IFS和TOPSIS法的城市基础设施PPP项目的风险评价更为科学合理，为政府将PPP模式应用于城市基础设施奠定了良好的基础。

[1] 胡 丽, 张卫国, 叶晓甦. 基于PPP模式的城市基础设施融资风险识别研究[J]. 甘肃社会科学, 2011, (1): 234-237.

[2] 向鹏成, 宋贤萍. PPP模式下城市基础设施融资风险评价[J]. 工程管理学报, 2016, 30(1): 60-65.

[3] 王慧莎. 基于PPP模式的城市基础设施项目融资风险研究[D]. 长沙: 中南大学, 2012.

[4] 王守清, 柯永建. 特许经营项目融资(BOT、PFI和PPP)[M]. 北京: 清华大学出版社, 2008.

[5] 王 哲. 城市公共基础设施PPP项目的融资模式研究[J]. 当代经济, 2016, (13): 20-21.

[6] 李凯风. 城镇基础设施建设PPP融资模式风险管理研究[J]. 求索, 2016, (1): 109-113.

[7] Fischer K, Leidel K, Riemann A, et al. An integrated risk management system (IRMS) for PPP projects[J]. Journal of Financial Management of Property and Construction, 2010, (15): 260-282

[8] Xu Y, Yeung J F Y, Chan A P C, et al. Developing a risk assessment model for PPP projects in China—A fuzzy synthetic evaluation approach[J]. Automation in Construction. 2010, 19 (7): 929-943

[9] Grimsey D, Lewis M K, Darrin. Evaluating the risks of public private partnerships for infrastructure projects[J]. International Journal of Project Management. 2002, 20(2): 107-118

[10] 张 萍, 刘 月. 城市基础设施PPP模式下融资风险水平度量研究[J]. 工程管理学报, 2015, 29(2): 65-70.

[11] 莫吕群, 陈振东, 郭霁月, 等. 基础设施PPP项目融资风险分析与案例研究[J].工程管理学报, 2016, 30(5): 71-76.

[12] 孙荣霞. 基于霍尔三维结构的公共基础设施PPP项目融资模式的风险研究[J]. 经济经纬, 2010, (6): 142-146.

[13] 李公祥, 尹贻林. 城市基础设施项目PPP模式的运作方式选择研究[J]. 北京理工大学学报(社会科学版), 2011, 13(1): 50-58.

[14] 陈 波, 徐成桂. PPP融资模式的风险分配方法[J]. 交通科技与经济, 2011, (1): 126-128.

[15] 王雪青, 喻 刚, 王佳冰. 高速公路项目融资风险的动态灰色模糊评价[J]. 重庆建筑大学学报, 2008, 30(5): 81-85.

[16] Atanassov K T. Intuitionistic fuzzy sets[J]. Fuzzy Sets and Systems, 1986, 20(1): 87-96.

[17] Hwang C L, Yoon K. Multiple Attributes Decision Making Methods and Application[M]. Berlin: Springer, 1981.

[18] Zadeh L A. Fuzzy Sets[J]. Information Control, 1965, 8(3): 338-353.

[19] 徐泽水. 直觉模糊信息集成理论及应用[M]. 北京: 科学出版社, 2008.

[20] 马义飞. 地下车库争议与城市停车难解决方案[J]. 建筑经济, 2008, (s1): 14-16.

[21] 俞 泳, 卢济威. 广场地下车库与城市行为[J]. 城市规划汇刊, 1998, (6): 46-48.