以问题为导向，增强学生总结概括能力——例谈求解几种三角函数最值题型的策略

崔允亮 毋晓迪

(1.河南大学数学与统计学院，河南 开封 475000； 2.广西民族大学理学院，广西 南宁 530000)

一、前言

在高考中，在函数的最值方面历来是命题者所青睐的，特别的以三角函数为桥梁的最值问题俨然成为高考中的热点导向。三角函数作为基本初等函数的范畴，它的最值问题恰是其性质和恒等变换的综合应用，也是描述周期现象的重要数学模型。而三角函数的最值问题往往会和其它知识进行交汇来命题，例如不等式、方程以及与几何有关的计算等等。如果学生能掌握并归纳出求三角函数的最值题型后，常见的三角函数最值问题都可以迎刃而解。

二、常见的几种三角函数最值题型以及策略

(一) y=asin x+b(或 y=acos x+b)型的函数

此类函数利用sinx≤1(或cosx≤1)即可求解，显然ymax=a+b,ymin=-a+b

例.在直角三角形中，两锐角为A和B，求sinAsinB的最大值.

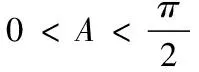
(二)y=a sin θ+b cos θ型的函数

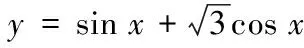
(三)y=a sin2x+b sin x cos x+cos2x型的函数

此类函数可先降次，再整理转化y=Asin(ωx+φ)+B形式解决.

例.求y= sin2x+2 sinxcosx+3cos2x的最小值，并求出此时的x的集合.

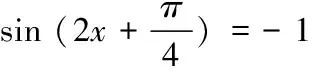
大部分含有上述三角函数的分式型都可以通过化简，然后利用三角函数的有界性来求解来处理等。

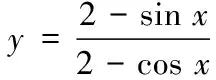
(五)含有“a sin x cos x,sin x±cos x”的三角函数的最值问题

例.求y=2sinxcosx+sinx+cosx的最大值.

三、总结

综上可得，相信通过这一归纳总结整理后，使学生和老师明白解决这类问题不仅涉及到三角函数的定义域、值域、图像、三角函数的恒等变换以及辅助角公式等，还会涉及到函数、不等式、方程以及几何计算等相关知识，是具有一定的综合性和灵活性。因此我们掌握这几种类型后，在解题中通过观察表达式的特点，选准解题策略，就会收到事半功倍的效果。

参考文献：

[1]代昆鹏.三角函数最值问题的讨论[J].数学教学与研究，2010(35).

[2]彭长军.三角函数最值问题的常见类型及其解法[J].高中数理化，2001(3).