刍议向量在新视域下高考数学中的“活跃性”探究

杨 宁

(河南师范大学数学与信息科学学院，河南 新乡 453007)

一、前言

鉴于向量同时兼备几何形式和代数形式这一特点，在和其他知识点交汇处命制高考题顺其自然就备受高考命题者所青睐。作为串联多个知识点交汇的媒介，在填空题和选择题方面其综合能力较强；在数学思想方面，重点设计到化归思想，数形结合思想以及分类讨论等数学思想。常见的主要有三角函数与向量的综合命题，函数与向量，不等式与向量以及压轴题圆锥曲线和向量的综合命题等等，最终都是以求代数问题而告终。而对于学生来说，主要考查学生的逻辑推理能力和运算能力等。同时也考查学生是否能综合巧妙的运用这些知识点去解决交汇问题的能力。本文例说高考数学中向量与其它知识的交汇及相关的解题策略。

二、向量与其他知识的交汇与融合

纵观近几年的考试，在向量的命题方面，单独命题的试题量甚微，但凡涉及到向量的试题都有一个明显的特点——加大了对交汇题的考查，充分体现了考试说明中“在知识交汇处”命题的一个基本原则。

(一)平面向量与平面几何的交汇

例 已知ΔABC中，∠C是直角，CA=CB，D是CB的中点，E是AB上一点，且AE=2EB，求证：AD⊥CE.

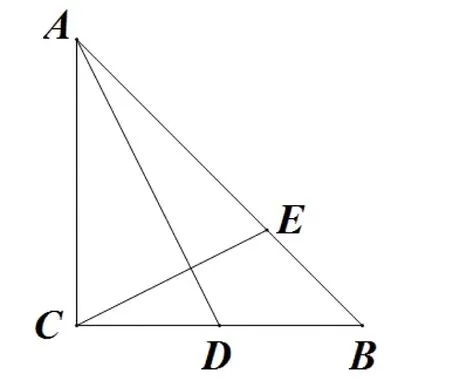
证明：建立如图所示的直角坐标系，设E(x,y)、A(0,a),则B(a,0).

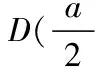
(二)平面向量与解析几何中的交汇

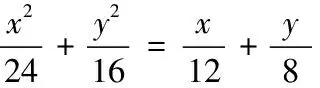
(三)平面向量与三角函数、函数等知识的结合

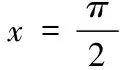
(四)平面向量与不等式的交汇

例 已知实数a、b、c满足a+b+c=0，且a2+b2+c2=1，求a的最大值.

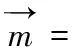
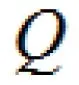
(五)向量与方程的交汇

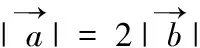
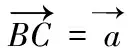
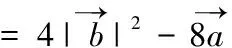
(六)向量与立体几何的交汇

(1)求证：DM⊥平面ABC；

(2)求二面角C-BM-D的大小.

证明：如图，取BD中点N，连结AN,CN∵将边长为2的正方形ABCD沿对角线BD折叠，使得平面ABD⊥平面CBD，∴AN⊥BD，CN⊥BD，

∵平面ABD⊥平面CBD，平面ABD∩平面CBD=BD，CN⊂平面CBD，CN⊥BD，∴CN⊥平面ABD。

以A为原点，AB、AD、AM所在直线分别为x轴，y轴，z轴，建立空间直角坐标系：则

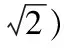
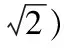
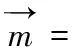
三、结语

新视域下，新课程增加了现代数学内容——向量。其目的不仅在于高中数学内容方面上的更新，更重要的是将新的思维方法带入了高中数学中来，因此可以更有效地处理和解决数学问题以及实际应用问题，也从中启示我们在高中学习数学时，应着重突出向量的工具性，注重向量与其它知识的交汇与融合，切忌讳深层次挖掘。

通过以上的例说，不难看出，借用向量知识，降低了很多题型的运算难度，同时也减小了运算量，向量知识在高中数学中作为一个新的知识，在学习数学中起到了至关重要的作用，在多个知识点交汇的地方完美的体现出了数与形的统一。我们在研究数学问题时，借助向量这个独特的工具，使我们能深刻的透过数学现象看出其中的本质问题，从而使问题得到相应的解决。

此外，在高考命题方面，命题专家会根据知识点交汇为突破口命题。作为教师，在高中数学中，常把其它问题进行化归，变成为简单的向量计算，其中将抽象的逻辑推理演变为具体的向量运算，实现了数与形的完美结合，所以平面向量为载体的数学试题与其它数学知识联系紧密，具有很强的时代气息，因此倍受命题老师的青睐。因此要正确引导学生把握常见题型的特点，让学生多次的反复熟悉其蕴含的数学思想以及解题方法，在考场上能应对自如，同时要注意符号的书写，抓住重点内容，轻松应考。

参考文献：

[1]吕世虎.高中数学新课程中的向量及其教学[J].课程·教材·教法，2006(1).

[2]金小欣.向量与其他数学知识的交汇[J].数学大世界·高中版，2005(4).

[3]李锋.平面向量与其他知识的交汇赏析[J].数理化学习(高中版)，2011(12).