等效电阻VMD-奇异谱熵双丝PMIG 焊稳定性评价方法

周晓晓，王克鸿，杨嘉佳，朱嘉宇，黄 勇

（南京理工大学材料科学与工程学院，江苏南京210094）

0 前言

焊接过程是一个存在强干扰强耦合的复杂物理化学过程，焊接过程工艺参数瞬态信号属于典型的非线性、非平稳信号，包含大量的焊接过程稳定性和焊接质量信息，相关学者对焊接过程稳定性进行了不同程度的研究[1-5]。目前非平稳信号处理及分析方法中小波变换[6]、经验模态分解（Empirical Mode Decomposition，EMD）、总体经验模态分解（Ensemble Empirical Mode Decomposition，EEMD）、局部均值分解[7]（Local Mean Decomposition，LMD）等方法已经得到广泛应用，但也存在一定的局限性。EMD算法虽然非常适合处理非线性、非平稳信号，但是存在模态混叠问题，EEMD为了解决该问题引入均匀分布的高斯白噪声，但同时也牺牲了原信号的纯洁性[8]。LMD算法虽然在减少迭代次数和抑制端点效应方面具有优势，但仍存在一定的模态混叠问题。KonstantinDragomiretskiy等人于2014年提出了全新的非平稳信号处理方法——变分模态分解（Variational Mode Decompo-sition，VMD）方法[9]，该方法是完全非递归的，并且由于其分模态数量K可根据待分解信号本身的特点预先设定，若选取合适，该方法能够有效避免模态混叠现象，呈现带通滤波特性。

本研究将VMD方法引入焊接过程工艺参数分析，先将铝合金双丝PMIG焊焊接过程电弧等效电阻信号进行模态分解，再计算由这些分模态构成的特征矩阵的奇异谱熵，进而提出电弧等效电阻VMD-奇异谱熵评价方法，并通过相关焊接试验及计算分析验证，证实焊接过程越稳定VMD-奇异谱熵越小，该方法对焊接过程稳定性的区分效果良好。

1 等效电阻VMD-奇异谱熵方法

1.1 等效电阻VMD方法

弧焊过程中电弧电导率受弧柱温度的影响，导致本应接近于电阻伏安特性的直流脉冲电弧动特性表现为电流上升段的电压大于电流下降段的电压[10]，采用等效电阻信号作为基础参数进行分析，避免单独采用焊接电流或者电弧电压信号进行分析时会丢失电弧的重要信息或者细节信息。

电弧等效电阻的计算公式为

式中 ut为瞬时电压；it为瞬时电流.

铝合金双丝PMIG焊焊接过程前后电弧电流信号、电压信号及由其计算所得的等效电阻波形示例如图1所示，其对应的焊接工艺参数如表1所示。

针对焊接电弧等效电阻信号进行VMD分解，将EMD方法中本征模态函数（IntrinicModeFuction，IMF）的概念重新定义为一个调幅调频信号[7]

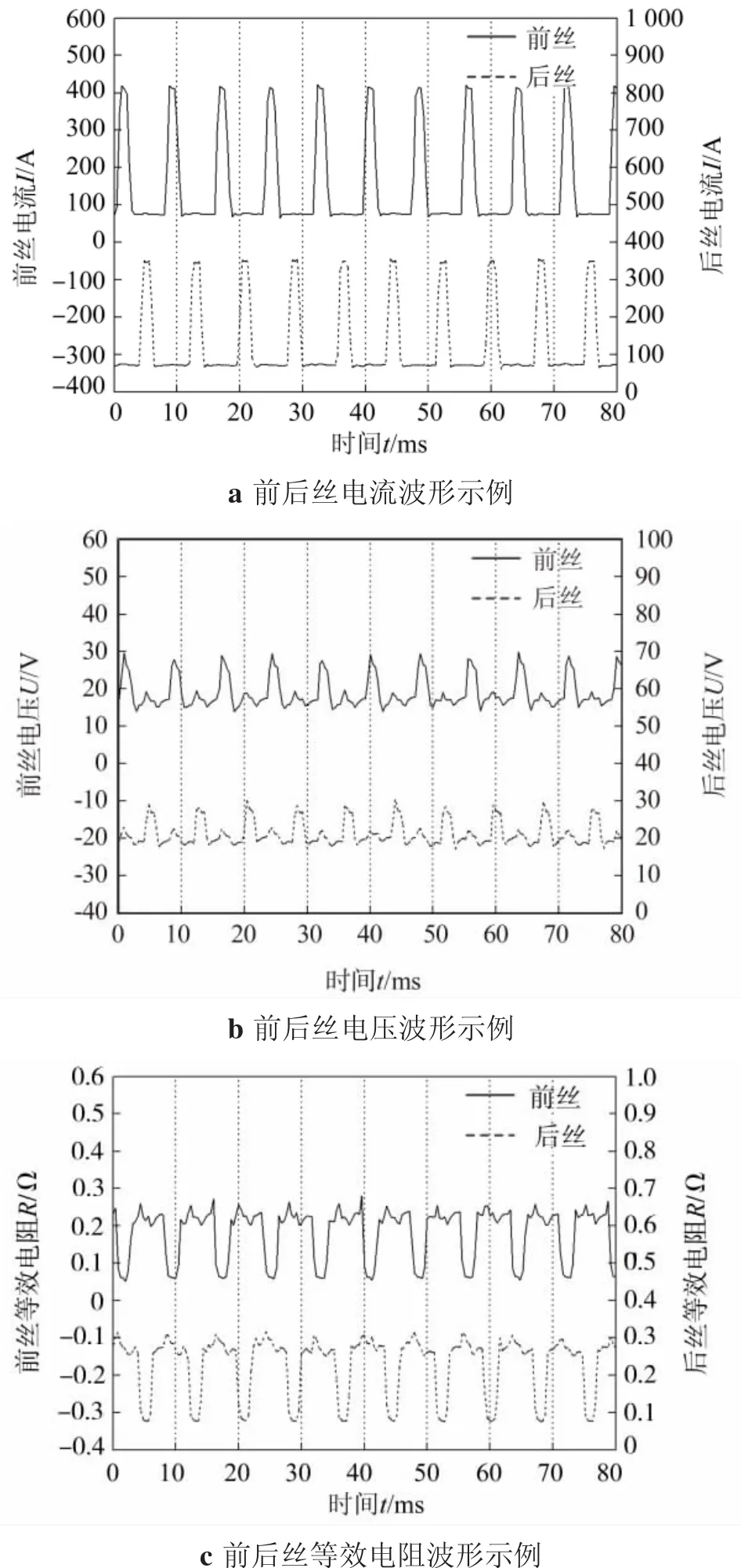
图1 焊接过程电流电压及等效电阻波形示例

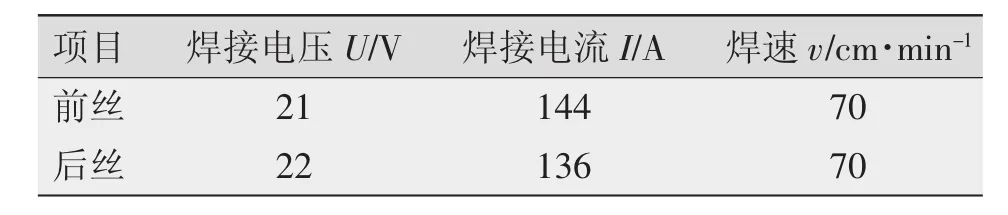
表1 焊接工艺参数

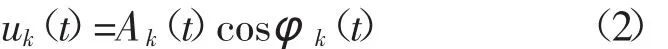
式中φk（t）≥0；包络线Ak（t）为非负函数；包络信号Ak（t）和瞬时频率ωk（t）=φ′k（t）变化均远慢于相位φk（t）的变化速度。

变分模型构造步骤：①为了得到信号的单边频谱，通过希尔伯特变换得到K个模态函数的解析信号。②通过指数修正K个模态函数，围绕其各自估算的中心频率调制到相应基频带。③通过高斯平滑解调信号获得每段带宽，即L2范数梯度的平方根。构造出受约束的变分模型为

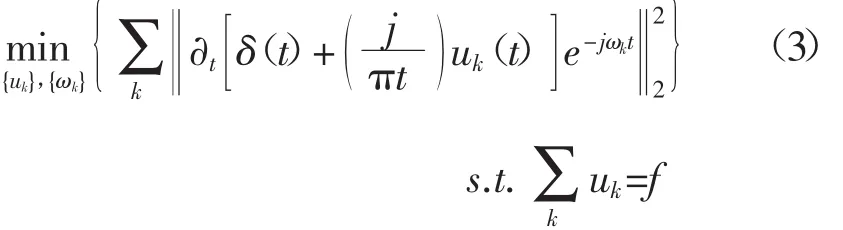
式中 {uk}={u1，u2，…，uk}为各模态函数；{ωk}={ω1，ω2，…，ωk}为以上各模态对应的中心频率；为各模态函数的和；f为原信号。

为求得上述约束问题的最优解，即得到原始信号的各模态分量，引入惩罚因子α构造增广Lagrange函数

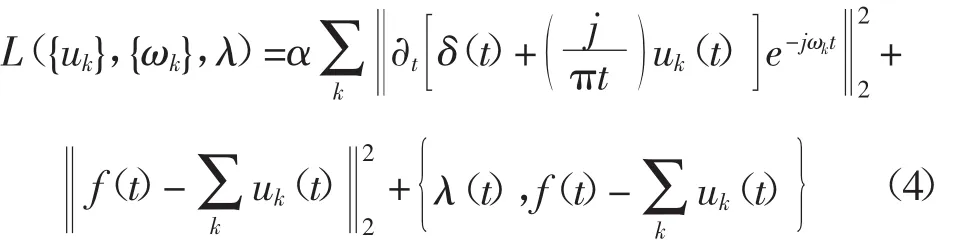
式中 α为惩罚参数；λ为Lagrange乘子。

将上述Lagrange函数从时域变换到频域，并进行相应的极值求解，分别得到模态分量uk和其中心频率ωk的表达式

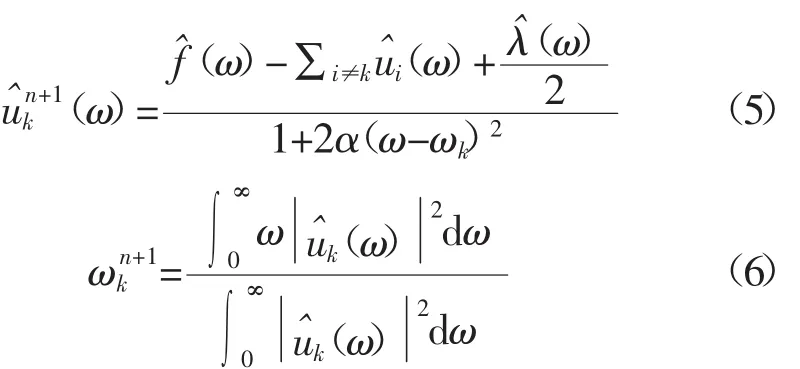
然后利用交替方向乘子算法求以上变分问题的最优解，从而将原始信号分解为K个窄带模态分量。算法过程如下：

（2）根据式（5）和式（6）更新和；

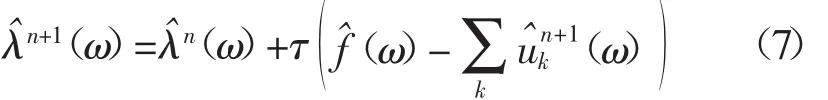
1.2 基于VMD的奇异谱熵

香农（Shannon）在研究信息的不确定性问题时提出，如果系统包含N个可能的事件，发生的概率分别为pi（i=1，2，…，N），并且有那么该系统的平均信息量即信息熵为

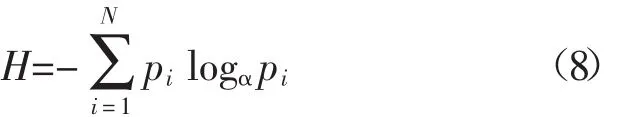
采用VMD方法对铝合金双丝PMIG焊前后电弧的等效电阻进行分解，得到K个IMF分量，u1，u2，…，uK，它们分别包含原始信号在不同频率的特征。因此，将K个IMF分量组成一个模态矩阵

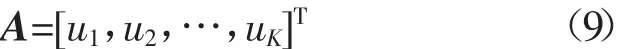
对模态矩阵A进行奇异值分解，获得模态矩阵的奇异谱 λ1，λ2，…，λK。奇异值描述信号在采样时间内各频段的特征，其大小反映焊接过程电弧等效电阻的差别。为定量描述这种变化程度，引入上述信息熵理论，构造信号的奇异谱熵

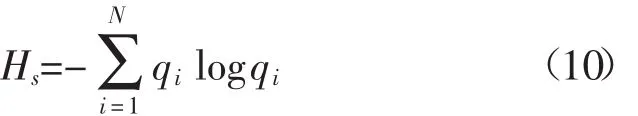
2 试验方法

焊接试验采用法国SAF公司的STARMATIC R450 TOPMAG自动双丝焊接系统。试验母材选用3A21铝合金板，尺寸 300mm×150mm×6mm，采用φ1.6mm的ER1100纯铝焊丝，保护气体为纯Ar（99.99%）。采用南京理工大学自主研发的熔化极气体保护焊专用采集装置进行焊接过程中电流电压信号的传感采集，该装置主要由电流电压传感器、滤波放大电路和模数转换采集卡组成，试验系统示意如图2所示。

为了得到焊接过程稳定性不同的电流电压信号，采用相同的焊接工艺参数（见表1），通过改变焊接过程中保护气流量与工件表面清洁程度等方式使焊接过程的稳定性发生变化。并用采集装置以2 500 S/s的采样率采集焊接过程中的电流、电压参数。工件表面清洁状态与保护气流量如表2所示，其中 1、2、3 组为清洁状态对比组，1、4、5 组为保护气对比组。

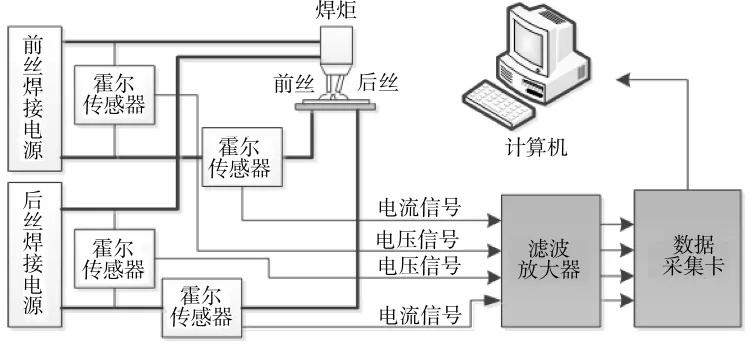
图2 试验系统示意

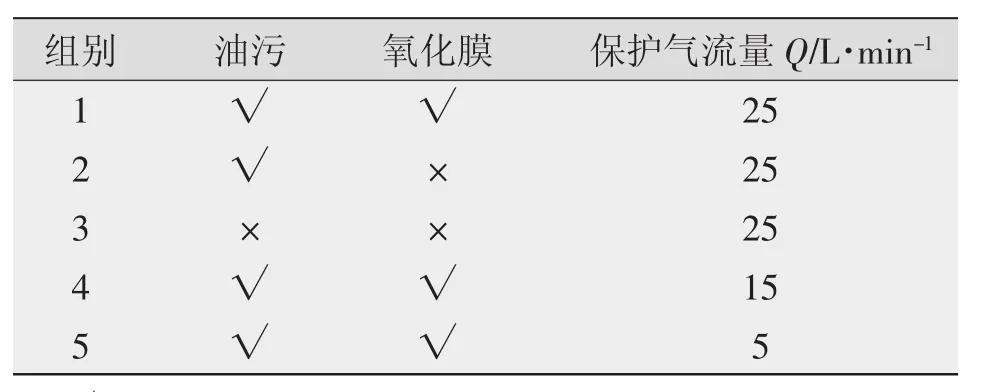
表2 工件表面清洁状态及保护气流量

焊接工件表面清洁处理包括去除工件表面油污及工件表面氧化膜两项工作。

本研究对焊接过程稳定性的评价主要基于焊接过程中的观察及焊缝成形质量评价。焊接过程中的观察主要指观察电弧声、熔滴过渡与电弧漂移等现象，而焊缝成形质量主要从焊缝宽窄差、余高高低差、鱼鳞纹、裂纹、气孔、咬边等方面考察。

3 试验结果与讨论

VMD算法中分模态个数K和惩罚因子α对分解结果影响很大，首先采用频谱观察法确定其分模态个数，然后采用互信息方法确定α取值。对焊接过程等效电阻信号进行傅里叶变换得到其频谱，信号的主要频率分量个数为7，同时直流脉冲信号存在直流分量，其分模态个数确定为7+1即K=8。互信息表示两个时间序列之间的相关性，互信息越大表示两序列的相关性越大。利用上文确定的K值，令α由1 000开始计算VMD分解后各IMF分量与原始信号之间的互信息并求和，和最大时α值最佳，本研究中最佳α值为2 500。用此K、α组合对前后电弧等效电阻信号进行分解，第1组试验焊缝中选取的一段前丝电弧等效电阻下号的分解结果如图3所示，从上到下为中心频率递增的IMF波形，分模态函数重构波形与原始信号的对比如图4所示，各分模态完整地重构了原始信号。

图3 VMD分解结果示例

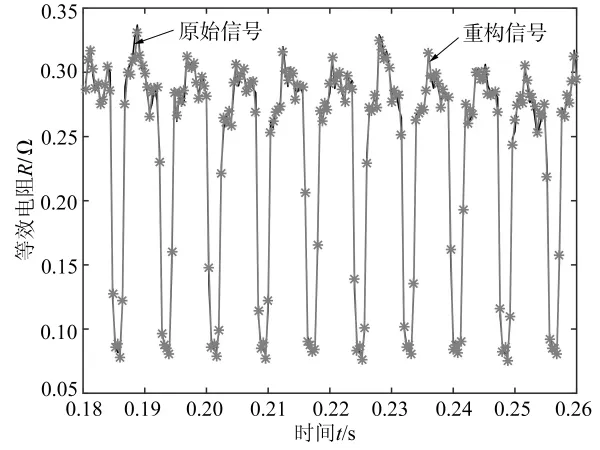
图4 重构结果与原信号对比

表面清洁状态对比组和保护气流量对比组的焊接过程电弧等效电阻VMD-奇异谱熵结果如图5所示，其中Rf为前丝电弧等效电阻，Rb为后丝电弧等效电阻。图5a对应的第1组试验焊接过程最为稳定，焊接过程中电弧声均匀、基本无飞溅、焊缝鱼鳞纹均匀、熔宽余高均匀且润湿好；第2组试验稳定性次之，焊接过程中电弧偶尔有噼啪声，飞溅明显，焊缝存在一定量的表面气孔、鱼鳞纹较均匀，润湿性稍差；第3组试验焊接过程最不稳定，电弧噼啪声频繁，飞溅很多，焊缝表面存在大量气孔与黑色浮渣焊缝余高熔宽很不均匀差值均可达2mm，且润湿性最差。等效电阻VMD-奇异谱熵对焊接过程稳定性十分敏感，并焊接过程越稳定，等效电阻VMD-奇异谱熵值越小，焊接过程越不稳定，VMD-奇异谱熵值越大。同样，焊接过程中保护气流量越小，保护气对空气的隔离效果越差，焊缝中越容易形成气孔和氧化夹渣，对应的焊接过程越不稳定，1、4、5组奇异谱熵值随着保护气流量的减少而增大（见图5b），与图5a结果一致。

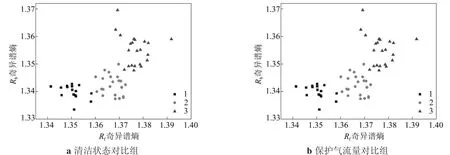
图5 不同稳定性的电弧等效电阻VMD-奇异谱熵图

以上示例及其他试验证实，铝合金双丝PMIG焊接过程越稳定，焊接过程前后电弧等效电阻的VMD-奇异谱熵值越小，反之则越大。在相同焊接工艺参数条件下，焊接过程等效电阻VMD-奇异谱熵能很好预测和评价铝合金双丝PMIG焊焊接过程稳定性。

4 结论

（1）基于焊接过程电弧等效电阻信号较单独的电流或弧压信号包含的电弧变化信息更全面，提出等效电阻VMD-奇异谱熵方法来评价铝合金双丝PMIG焊焊接过程稳定性。

（2）采用信号频谱观察法并结合互信息方法确定VMD方法关键参数K和α，将等效电阻信号成功地分解为K个包含原信号在不同频段特征的IMF分量，避免模态混叠线性并能完整地重构原信号。

（3）焊接过程越稳定其对应的等效电阻VMD-奇异谱熵值越小，反之则越大。在相同的焊接电流、电压条件下，焊接过程等效电阻VMD-奇异谱熵可以很好地预测和评价焊接过程稳定性。

参考文献：

[1]Ye D，Hua X，Zhang J，et al.Analysis of arc interference and welding stability in twin wire GMA welding[J].The International Journal of Advanced Manufacturing Technology，2015，81（1）：627-633.

[2]陈华斌，孔萌，吕娜，等.视觉传感技术在机器人智能化焊接中的研究现状[J].电焊机，2017，47（3）：1-16.

[3]郭勇，李志勇，赵洪志，等.基于LabVIEW的焊接过程多信息分析平台[J].电焊机，2012，42（4）：8-22.

[4]陈善本，吕娜.焊接智能化与智能化焊接机器人技术研究进展[J].电焊机，2013，43（5）：28-36.

[5]周晓晓，王克鸿，杨嘉佳，等.等效电阻模糊熵双丝PMIG焊稳定性评价方法[J].焊接学报，2017，38（7）：107-110.

[6]洪波，戴江平，李振凯，等.基于经验小波变换的磁控埋弧焊焊缝跟踪信号分析[J].焊接学报，2017，38（6）：37-40.

[7]孙洁娣，肖启阳，温江涛，等.基于LMD包络谱熵及SVM的天然气管道微小泄漏孔径识别[J].机械工程学报，2014，50（20）：18-25.

[8]李昌林，孔凡让，黄伟国，等.基于EEMD和Laplace小波的滚动轴承故障诊断[J].振动与冲击，2014，33（3）：63-69.

[9]Dragomiretskiy K，Zosso D.Variational Mode Decomposition[J].IEEE Transactions on Signal Processing，2014，62（3）：531-544.

[10]殷树言.气体保护焊工艺基础[M].北京：机械工业出版社，2007.