等覆盖率变径编织方法

吴杰伟， 孙志宏， 郁 强， 陈燕婷， 邱夷平， 周其洪， 陈晓川

(1. 东华大学 机械工程学院， 上海 201620； 2. 东华大学 纺织学院， 上海 201620)

编织是一种传统的纺织技术，初期主要应用于鞋带、绳缆、装饰带的编织。如今，编织物在航空航天、电缆、医疗等领域的应用已成为一种常态。在这类行业的应用中，仍然有许多难题需要解决：首先是编织物的质量，主要有纤维的连续性，与曲面的贴合性，纤维分布的均匀性；其次是生产效率，如自动化和批量化生产。研究人员针对纤维分布的均匀性做了大量的研究，认为编织角决定了纤维的运动轨迹，进而影响编织物表面覆盖系数、纱线体积系数；因此，国内外研究者建立了一系列关于编织角的预测模型：Zhang等[1-2]对等径管状编织物进行了研究，考虑纱线的摩擦和滑移等因素的影响，建立了编织角预测的力学模型；Du等[3]建立了编织对称旋转曲面的数学模型，可预测编织物的局部编织角与编织半径之间的关系，以及编织物表面覆盖系数和纱线体积系数；Guyader等[4]建立了编织非对称曲面的数学模型，在已知芯轴几何形状、织物牵引速度和纱锭角速度的条件下，通过在编织点建立关于纱线运动的局部坐标，预测芯轴上各点的编织角；Ravenhorst等[5]设计了1种可旋转的导纱环，以逆运动学为基础计算编织不同截面芯轴所需的牵引速度和导纱环的运动规律；文献[6-7]通过有限元分析模型与实验相结合的方法得到编织物的图像，该方法能够检测编织缺陷以及纱道之间的相互作用；Potluri等[8]基于纱线的微观结构和重复单元进行微机械建模，得到编织物的力学性能。

以往建立的编织模型都是预测编织物的编织角、编织物覆盖率等，而对如何控制牵引速度与纱锭角速度之间的比例关系，从而实现变直径等覆盖率编织的研究却未见报道。在信号线屏蔽层的生产过程中，编织覆盖率是衡量产品质量的一个重要指标，因此，在已知编织覆盖率的条件下，建立芯轴牵引速度和纱锭角速度的比率系数的预测模型，对实际生产具有重要指导意义。本文以旋转对称曲面芯轴为例，并以一恒定的编织覆盖率和纱锭角速度为前提，确定各项编织工艺参数和结构参数之间需要满足的函数关系，最终建立牵引速度的预测模型，并应用MatLab和SolidWorks仿真验证模型的可靠性。

1 编织结构的分析

在编织过程中，相互交织的纱线会产生摩擦和滑移，进而产生弯曲，给分析增加了许多困难。根据本文研究的对象(旋转对称曲面芯轴)作出以下 3个假设，并基于这 3个假设条件进行分析：

1) 芯轴为轴对称结构，编织盘为圆形，忽略纱锭的S型运动，纱锭简化为旋转半径为r的圆周运动；2) 所有的纱线在芯轴上重复缠绕，因此，仅需分析单根纱线的运动情况；3) 在收敛区内，纱线不产生任何弯曲，即忽略收敛区内纱线交织产生的影响。

编织角主要有2种定义：一种为纱线与其所包缠芯轴表面母线之间的夹角；另一种为纱线与其所包缠芯轴表面的水平切线之间的夹角。这2个角存在互余关系，本文编织角指的是第1种定义，即纱线与芯轴表面母线之间的夹角，用θ表示。当芯轴为等径芯棒(即圆柱状)时，编织角θ由牵引速度v、纱锭的角速度ω以及芯棒半径r共同决定，计算公式如式(1)所示。

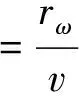
(1)

当芯轴是锥角为γ的圆锥体，其轴向与z轴同向时，编织角由编织成型速度vzz、纱锭的角速度ω、芯轴局部半径rm和芯轴锥角γ共同决定[3]，参数间的函数关系如式(2)所示。

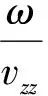
(2)

式中：rm、γ分别表示编织点的芯轴半径和锥角，前者是关于芯轴轴向位置z的函数。

图1示出纱线在收敛区的缠绕三维图。其中：芯轴的局部锥角为γ；导纱环半径为rg；编织点处芯轴半径为rm；收敛区长度为h(即编织点距导纱环的距离)，是关于位置z的函数；S为芯轴的母线长度；dz表示极小段的芯轴段；drm是该段芯轴2个平面的半径差；θ为该编织点的编织角，是关于位置z的函数。

图1 纱线在收敛区的缠绕三维图Fig.1 Three-dimensional diagram of yarn winding in convergence region. (a) Front view; (b) Side view; (c) Overhead view

根据几何关系可得到编织物的编织角预测模型[3]，如式(3)所示。

(3)

2 牵引规律模型的建立

2.1 编织覆盖率的几何分析

纱线的总面积与被包缠芯轴表面积的比率称为编织覆盖率(C)，当纤维宽度wy>>τ(纤维厚度)时，可忽略纤维交织产生的起伏，本文以下推论都在该前提下进行。根据编织结构的重复性，编织覆盖率定义为在一个编织单元中的纱线面积Sl与单元总面积Sc的比率，如式(4)所示。其中：Sm表示芯轴被包裹的总面积；Sw表示纱线的总面积。

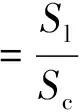
(4)

纱线在芯轴上的缠绕是一个动态过程，牵引速度、纱锭角速度以及芯轴表面形状决定了编织结构。通过对编织过程进行动态分析，可建立牵引速度等工艺参数与编织结构参数的函数关系。图2示出其动态编织过程，其中，rm为编织点处的芯轴半径，γ为锥形芯轴的锥顶角，经过单位时间dt纱锭转过的角度为dβ，芯轴在牵引速度v的作用下沿芯轴轴线OO′移动dz，在二者作用下，纱线在芯轴表面的缠绕路径为P→P′,编织半径的变化量为drm。

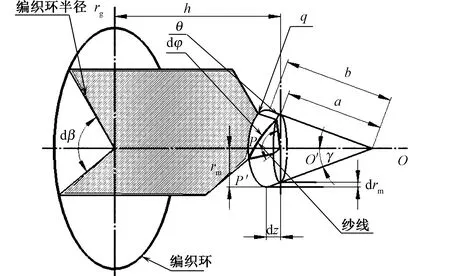
图2 动态编织过程Fig.2 Dynamic weaving process

根据几何关系可知，当0°<γ<90°时，母线长度a和b分别为：

(5)

(6)

当编织角为0°或90°时，2θ为0°或180°，交织的纱线相互平行，此时，所有纱线平行缠绕在芯轴上，这种情况下，纱线不存在交织，因此，θ角应满足0°<θ <90°[1]。

为使问题简化，将立体圆锥沿母线展开成扇形，将空间问题转化为平面问题，再对圆弧进行几何求解。图3示出编织物的平面结构。假设纱锭的个数为n，如图3(b)所示，编织角为θ，纱线宽度为wy，相邻纱线之间的间隙为δs，wc和δc分别为wy和δs在斜切面上的长度，则几何关系如式(7)、(8)所示。

(7)

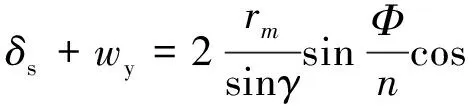
(8)

式中，Φ表示芯轴展开图的圆心角，由圆锥的侧面积公式可知：

Φ=2πsinγ

(9)

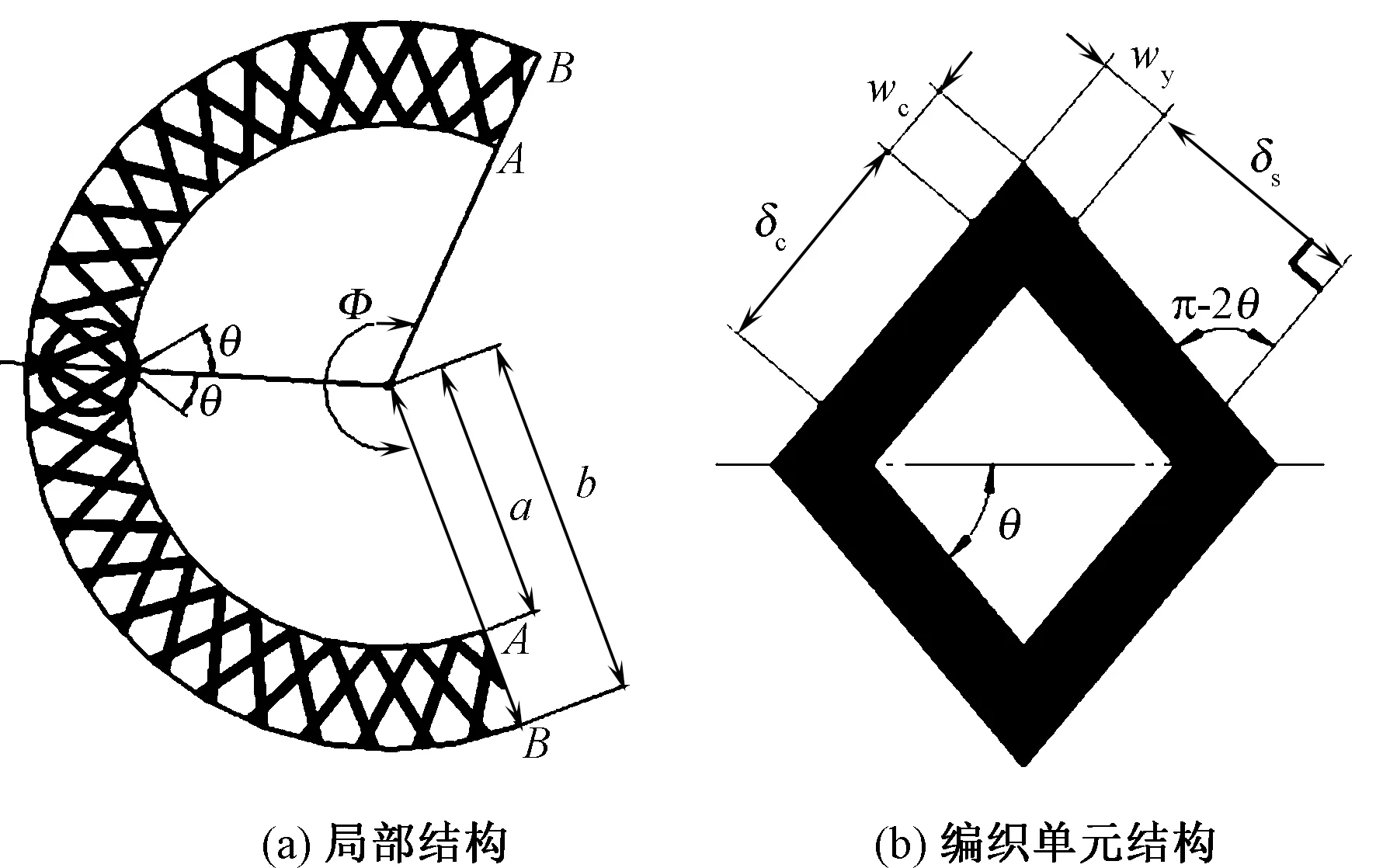
图3 编织物的平面结构Fig.3 Plane structure of woven fabric. (a) Local braided structure； (b) Cell structure diagram

将式(8)和(9)代入式(7)，可得：

(10)

由菱形面积公式可求得编织单元内纱线的面积Sl和单元结构的面积Sc分别为

Sc=2(δc+wc)2sinθcosθ

(11)

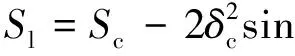
(12)

由式(4)、(11)、和(12)可知编织覆盖率为：

(13)

将式(7)、(8)和式(10)代入式(13)并简化，得到

(14)

式中:0°<γ<90°; 0°<θ<90°。

当γ=0°时，局部芯轴为圆柱管，此时编织展开图和单元结构图如图4所示。

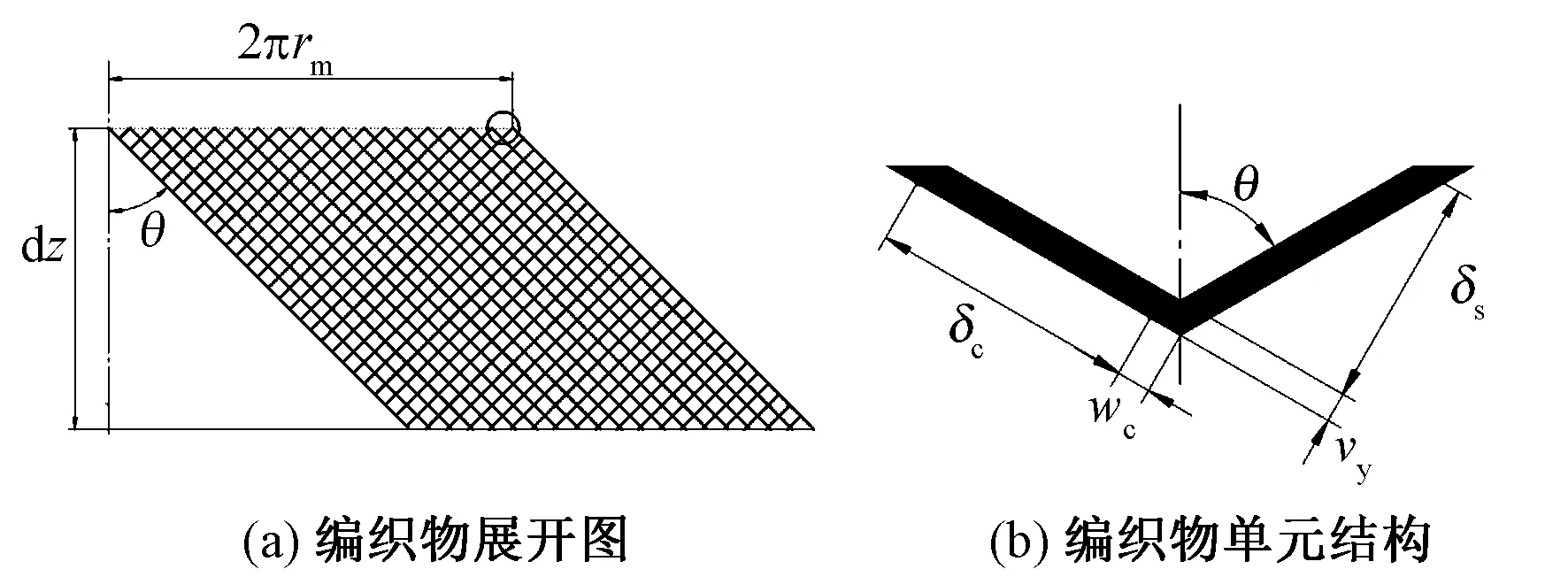
图4 等径圆管的编织物平面结构Fig.4 Plane structure of woven fabric on circular mandrel with constant diameter. (a) Structure of fabric; (b) Cell structure of fabric

由图4可知编织展开图是一个平行四边形，因此有如下表达式：

drm=0

a=b→+∞

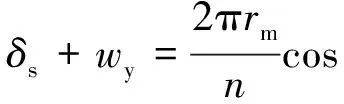
代入式(13)中，可得

(15)

当γ=90°时，dz=0，显然这种情况不合理。

2.2 编织覆盖率与编织参数的函数关系

当0°<γ<90°，令：

当纱线宽度wy和纱锭数量n为定值时，P是γ角的函数。例如，当n=32，wy=1 mm时，若γ角由 -40°变化为40°，γ与P的关系如图5所示。

图5 P值的变化曲线Fig.5 Variation curve of P value

因此，当0°<γ<90°时，

≈5.097

当γ=0°时，P=2π/n=5.093；当0°≤γ<90°时，P值近似为常数。

由式(14)、(15)可知，编织覆盖率C是关于编织角θ和编织点半径rm的函数。当wy和n保持恒定，rmcosθ为定值时，编织覆盖率在单位表面的值保持恒定，因此：

(16)

式中：

当C为一恒定值，则K为一个常数。

2.3 编织牵引速度的求解方法

已知编织速度(牵引速度和纱锭的角速度)，求解编织结构参数(编织角、芯轴锥角、编织半径等)称为正解法；已知编织结构参数，求解编织速度，称为逆解法[2]。实际生产中，已知芯轴的轮廓曲线，根据前文的结论可得到编织覆盖率与编织角的关系，因此，本文采用逆解法求解牵引速度与纱锭角速度的配比关系，及括编织点高度的变化规律。

编织过程中，牵引速度可分解为2部分：一是编织点的运动速度vh(即Δt时间内，编织收敛区长度的变化量，其中速度方向取芯轴运动方向为正)；二是正在编织的纱线的运动速度vz。收敛区长度h由牵引速度v、纱锭的角速度ω以及芯轴的半径rm共同决定[1-3]，随着v与ω比率以及编织半径rm的变化，收敛区长度h也相应地发生改变(即编织点高度沿竖直方向上下或水平方向移动)。其计算公式为：

(17)

式中，z表示编织物的长度，是关于时间t的函数。

由式(2)、(3)可知：

(18)

整理得：

γ-rg2+rm2=0

(19)

2.4 编织牵引速度的求解

采用逆解法求解牵引速度v和纱锭角速度ω，自变量为编织长度z，z是关于时间t的函数，此时v和ω有无数组解，并且由式(2)可知，二者存在一定的耦合关系。考虑操作的简便性，同时减少惯性带来的延迟，将ω设为一个合理的常数，最终可求解v。

已知芯轴的轮廓曲线为

芯轴总长为L，将芯轴沿着z轴均匀分成n段(n→∞)，则Δz=L/n，在Δz足够小的条件下，该段芯轴的芯轴锥角γ可认为是恒定的，再将该段芯轴等分成m段(m→∞),此时问题即转化成n段圆锥台状的积分问题；但是，如果Δz已经足够小，编织半径rm的变化量将趋于0；因此，取每段芯轴的起点半径和终点半径之和的平均值作为该段芯轴的编织半径rmi,如式(20)所示。

(20)

式中：i=zj,j=1～n；γi=na0zn-1+n-1a1zn-2+n-2a2zn-3+…+2an-2z1+an-1

将式(20)代入式(16)，可得Rmi所对应的编织角θi为：

(21)

式(19)是关于编织角θ、芯轴锥角γ、编织点半径rm、收敛区长度(编织点高度)h的函数式，即关于Z的函数。由式(20)、(21)可知，式(19)是关于h的一元二次方程，通过求解可得编织芯轴上各点的编织点高度为：

(22)

其中：

b=2rmitanγi

c=rmi2-Rg

h是关于自变量z的函数，即关于i的函数，Δt表示编织Δz长度的编织物所需的时间，由式(18)可知：

ti=z/Vzi=

(23)

因此，Δti时间内编织点高度的变化量为：

Δhi=hi+1-hi

(24)

编织点沿轴向的位置变化速度为：

(25)

综合式(18)～(25)求得牵引速度表达式为：

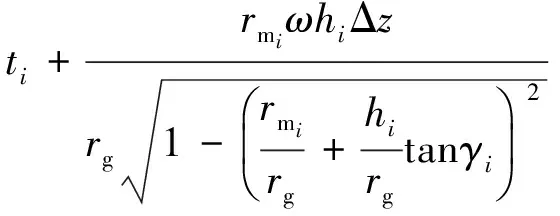
(26)

已知编织覆盖率C，芯轴各段的半径rmi以及对应的芯轴锥角γi，通过式(14)、(15)确定芯轴每段的编织角θi，将所得的θi代入式(21)、(22)、(26)，最终求得各位置的编织点高度hi和牵引速度vi。

变直径编织过程中，当编织覆盖率保持恒定，由式(22)、(26)可知，编织点高度和牵引速度都随编织半径的变化而变化。当编织点高度与设计的编织点高度不同，改变编织机的牵引速度，会导致编织角的变化，但是编织角的变化不是瞬时的[9]。本文Δz趋于0，即编织半径的变化量趋于0，编织点高度和牵引速度的变化量都将极小，编织角的不稳定区可忽略不计。

3 模型的仿真验证

3.1 理论模型分析

实际生产中，芯轴轮廓往往是曲线，即芯轴锥角和半径沿芯轴的轴线方向不断变化。从积分的角度分析，曲线可看成有限个不同倾角的线段组合而成，外形轮廓为曲线的芯轴可等价为有限个不同锥角的圆锥台组合而成；因此，首先在不同编织覆盖率的条件下，仿真分析编织圆锥台状芯轴；其次，仿真分析编织由多个不同锥角的圆锥台组合而成的芯轴，分别分析其编织点高度，牵引速度以及编织角的变化曲线。

本文选择2种不同形状的芯轴进行仿真如图6、7所示。其中：图6为最简单的管状变直径芯轴，该芯轴仅有1种固定的倾角，复杂形状的管状芯轴是由无数段这类芯轴组成；图7为杯状芯轴，其包含了半径变大，倾角变大和倾角变小；半径变小，倾角变大和变小的情况；因此，该芯轴包含了所有的芯轴变化情况。

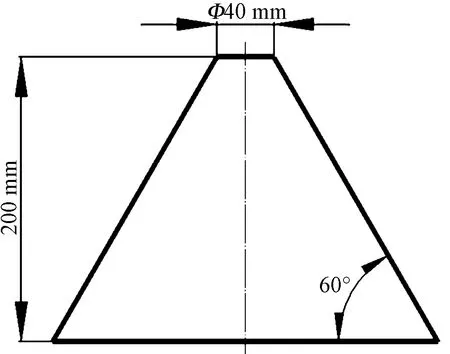
图6 圆锥台状芯轴Fig.6 Conical shaped mandrel

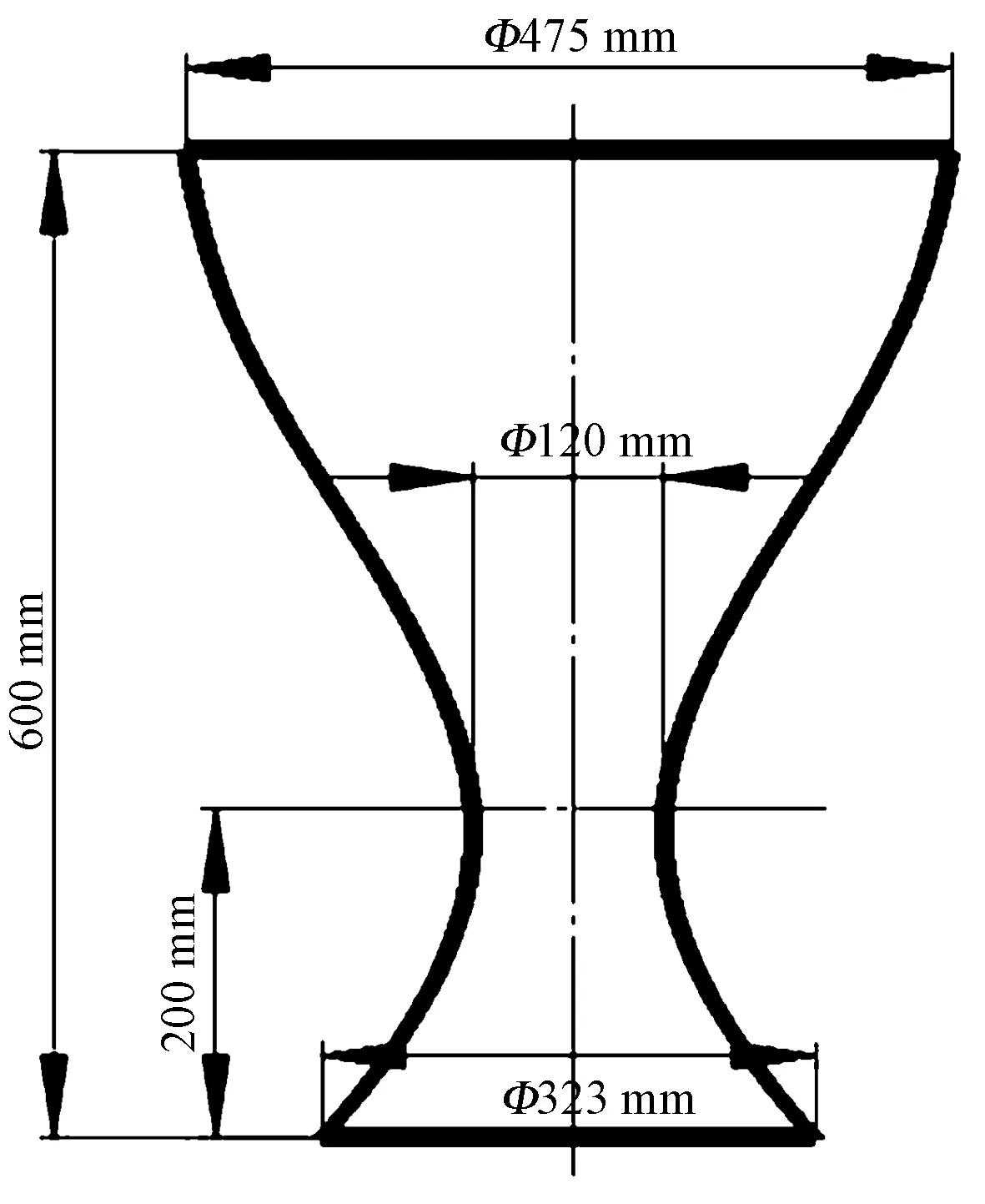
图7 杯状芯轴Fig.7 Cup shaped mandrel

采用扁丝进行编织，丝束宽度wy为2 mm，纱锭数为32，纱锭角速度为10 r/min，导纱环半径rg为600 mm，编织覆盖率分别设定为84%、75%、64%。观察编织角变化趋势和牵引速度曲线。图8、9分别示出编织图6、7所示形状织物过程中的各项参数变化情况。

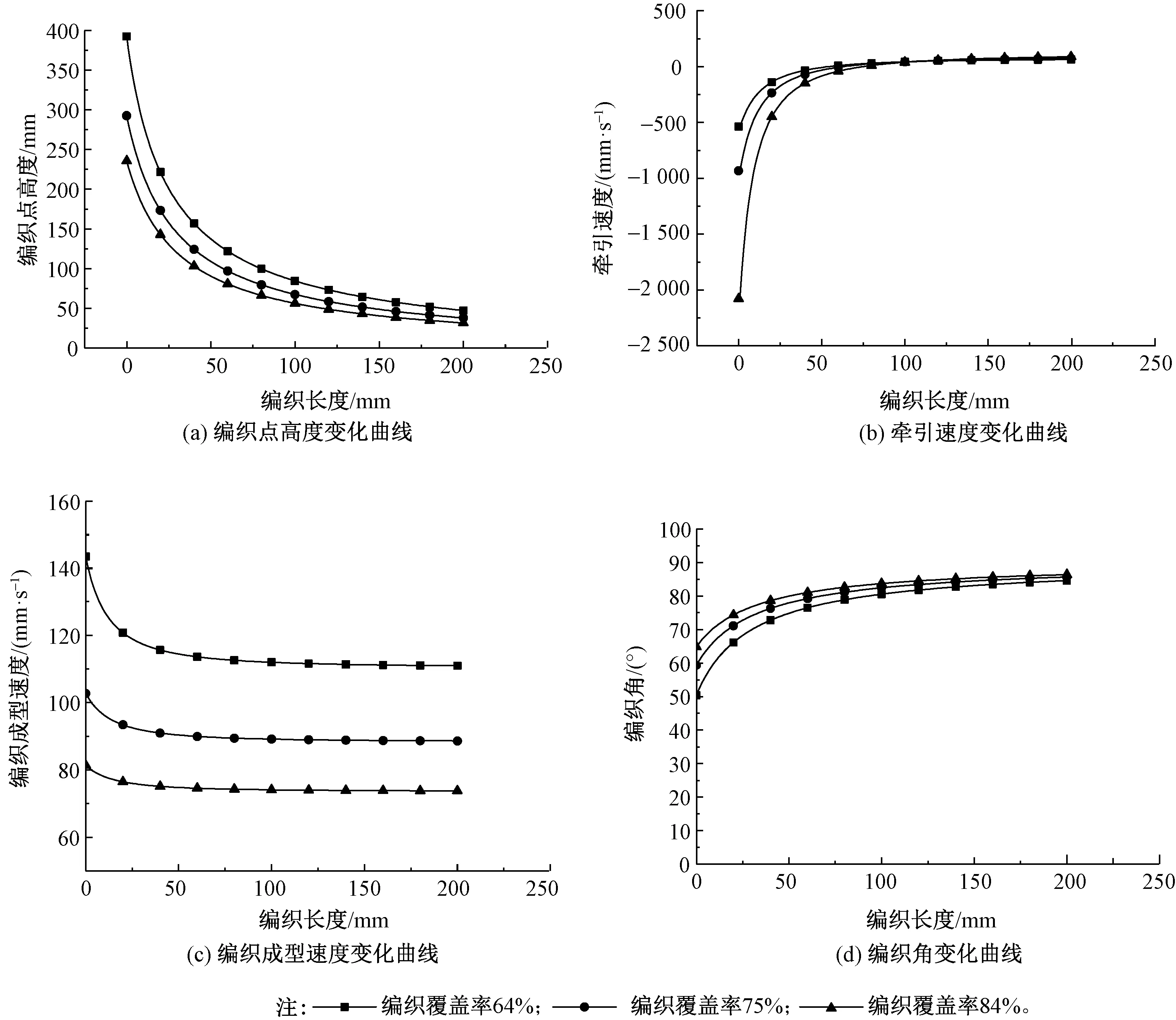
图8 圆锥台状织物的各项工艺参数Fig.8 Process parameters of conical shaped fabric. (a)Variation curve of braiding point height; (b)Variation curve of tractive speed; (c)Variation curve of braiding speed; (d)Variation curve of braiding angle

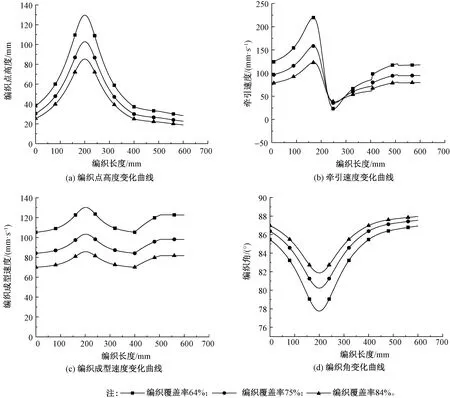
图9 杯状织物的各项工艺参数Fig.9 Process parameters of cup shaped fabric. (a)Variation curve of braiding point height; (b)Variation curve of tractive speed; (c)Variation curve of braiding speed; (d)Variation curve of braiding angle

由图8可看出:在保持恒定的覆盖率和芯轴锥角γ条件下，随着编织半径的增大，编织角呈增大趋势，牵引速度和编织点高度呈减小趋势。在编织初始阶段，各项指标的下降或上升趋势都比较明显，但一段时间后明显减缓。由式(16)可知，编织半径与编织角的余弦呈反比关系，而余弦函数在(0，π/2)区间内的变化率是逐渐减小的，因此，当编织半径的变化值恒定时，编织角的变化由急到缓；编织覆盖率增大，芯轴上各点的编织角呈增大趋势，符合式(15)中二者的关系。编织点高度h，牵引速度v和vz呈下降趋势。

由图9可知，编织覆盖率越大，编织点高度、牵引速度、编织成型速度越小，编织角越大。

图10示出图7所示芯轴的芯轴锥角沿轴向的变化曲线。可看出：当z由0增加至400 mm时，即γ从-35°增长到35°过程中，芯轴锥角的变化值较小，芯轴锥角变化值Δγmax=1.074 1°，同时由图9(b)可知在该范围内牵引速度v的曲线比较光滑，无突变点。在z为400 mm处，γ由35°减小至30°，由图9(b)可知，牵引速度v由85.95 mm/s突变到108.45 mm/s，再下降到97.71 mm/s，然后逐渐上升；因此，当芯轴轮廓的芯轴锥角变化量小于5°时，牵引速度v无突变。当芯轴锥角变化量大于5°时，可在临界位置添加消极速度，使牵引速度平稳过渡[10]。

图10 杯子状芯轴的芯轴锥角变化曲线Fig.10 Variation curve of cone angle of cup like mandrel

3.2 三维模型的建立与预测模型验证

纱线在芯轴上的缠绕轨迹是轴向运动与平面运动的合成，其中平面运动包括轴向运动和径向运动，即以rm(i)为旋转半径，ω(t)为转速的圆周运动和在编织平面内以A为波峰,1/N为周期的径向正弦运动[11]。在沿z轴方向，纱线以速度v(t)作直线运动，其运动轨迹表达式如式(27)所示。其中x、y、z分别表示纱线上各点的直角坐标。将编织半径rmi和时间ti代入式(27)，可得出i点的坐标，类似地，可求得纱线轨迹上所有点的坐标，最终得到纱线运动轨迹。

(27)

为验证上述牵引速度预测模型的有效性，采用MatLab模拟仿真带芯编织，求得纱线的运动轨迹。将运动轨迹数据导入SolidWorks，通过建模以及阵列，最终得到编织物的三维仿真模型如图11、12所示。

图11 圆锥台状织物3-D模型Fig.11 3-D model of conical shaped fabric

图12 杯状织物3-D模型Fig.12 3-D model of cup shaped fabric

3.3 牵引规律预测模型的验证

芯轴单位侧面积上纱线的面积与其侧面积的比值称为纱线的编织覆盖率。当芯轴单位侧面积上包缠的纱线面积恒定时，编织覆盖率恒定；当纱线的宽度远大于纱线厚度时，可忽略纱线的起伏以及交织点处于下层的纱线面积，纱线的面积与其质量成正比例关系，因此，编织覆盖率可以等价成芯轴单位上所缠绕的纱线质量。在三维模型中将纱线材料设定为碳纤维Hexcel AS4C(3 000丝)。分别在芯轴不同位置截取相同长度的一段芯轴，计算各段芯轴的侧面积并称量其质量，求出纱线质量与芯轴面积的比值(单位面积内的纱线质量)。由于芯轴各段单位面积上纱线的交织点个数不同，因此，在忽略交织点处下层纱线质量条件下，各段芯轴上的纱线质量存在一定的偏差。图5所示圆锥台芯轴单元侧面积包缠纱线的质量测量结果如表1所示，组1～8为图11 所示模型中距上端40 mm开始，每隔20 mm取一段长度为8 mm的纱线模型。图6所示芯轴单元侧面积包缠纱线的质量测量结果如表2 所示，表中组1～8为图12所示模型中距左端 50 mm开始，每间端20 mm取一段长度为8 mm的纱线模型。纱线质量的最大偏差率计算方法如式(28)。

(28)

式中：mmax为最大单位面积内的纱线质量；mmin为最小单位面积内的纱线质量。

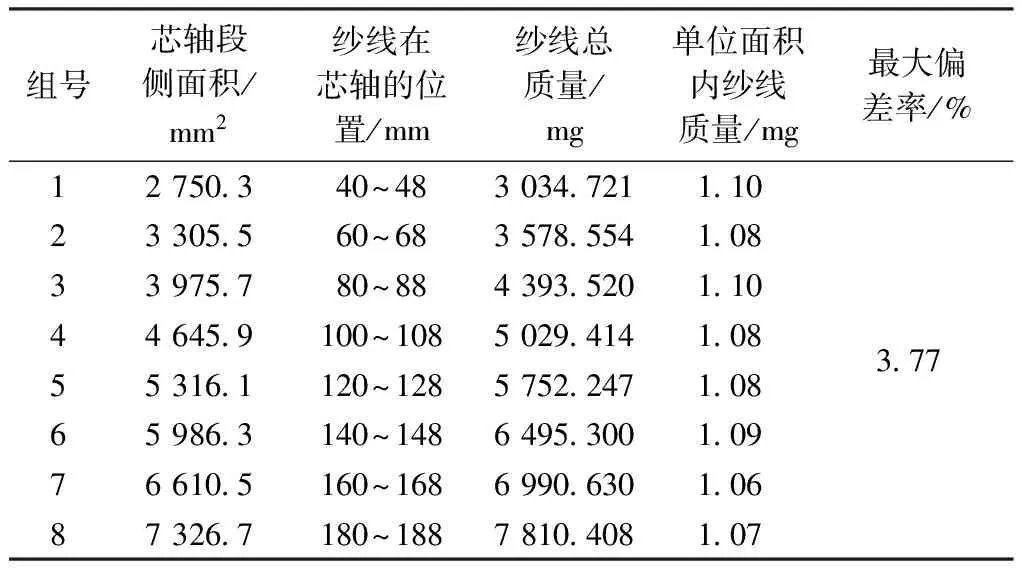
表1 圆锥台芯轴表面单元面积内的纱线质量与偏差率Tab.1 Yarn quality and deviation ratio in cellar area of surface of conical shaped mandrel

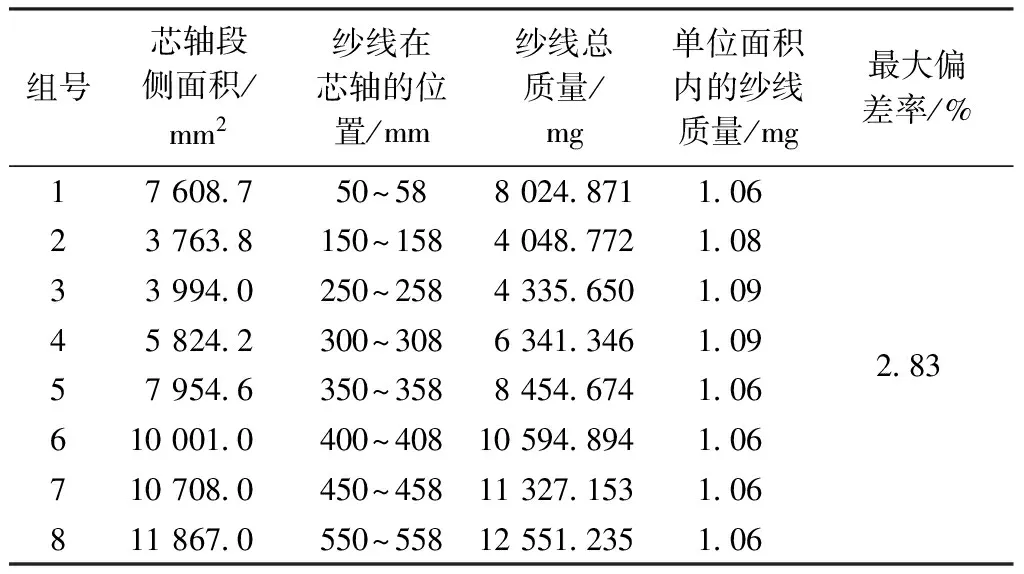
表2 杯子状芯轴表面单元面积内的纱线质量与偏差率Tab. 2 Yarn quality and deviation ratio in cellar area of surface of cup shaped mandrel

由表1可知，组1和组3单位面积的纱线质量最大，组7最小，芯轴轴向不同部位单位面积的纱线质量的最大差值为0.04 mg，偏差率为3.77%，符合要求。由表2可知，组3和组4单位面积的纱线质量最大，其余各组几乎一致，最大质量差为 0.03 mg，偏差率为2.83%，符合预期要求。上述仿真数据证明芯轴表面各段的编织覆盖率保持恒定，牵引速度v的数学预测模型准确可靠。

4 结 论

本文在已知的编织角预测模型基础上，建立编织覆盖率与编织角、芯轴半径、芯轴锥角等参数相关的数学模型。研究表明，在一定的芯轴锥角范围内，编织覆盖率只与编织半径和编织角相关，并且二者之间存在三角函数关系。采用逆解法，在已知芯轴各段半径和芯轴锥角的条件下，确定各段的编织角。在纱锭角速度恒定条件下，应用微积分方法求得牵引速度v的数学模型。最后通过MatLab和Solidworks软件模拟仿真编织物，并用单位面积纱线质量偏差率进行验证，最终结果表明该模型具有可靠性。

FZXB

参考文献：

[1] ZHANG Q, BEALE D, BROUGHTON R M. Analysis of circular braiding process: part 1: theoretical investigation of kinematics of the circular braiding process[J].Journal of Manufacturing Science and Engineering, 1999, 121: 345-350.

[2] ZHANG Q, BEALE D, BROUGHTON R M. Analysis of circular braiding process: part 2: mechanics analysis of the circular braiding process and experiment[J].Journal of Manufacturing Science and Engineering, 1999, 121: 351-359.

[3] DU G W, POPPER P. Analysis of a circular braiding process for complex shapes[J].The Journal of the Textile Institute, 1994, 85(3): 316-337.

[4] GUYADER G, GABOR A, HAMELIN P. Analysis of 2D and 3D circular braiding processes: modeling the interaction between the process parameters and the preform architecture[J].Mechanism and Machine Theory, 2013, 69: 90-104.

[5] RAVENHORSTVan J H, AKKERMAN R. Circular braiding take-up speed generation using inverse kinematics[J]. Composites: Part A, 2014, 64: 147-158.

[6] PICKETT A, ERBER A, VON REDEN T, et al. Comparison of analytical and finite element simulation of 2D braiding[J].Plastics, Rubber and Composites, 2009, 38(9/10): 387-395.

[7] RAWAL A, POTLURI P, STEELE C. Prediction of yarn paths in braided structures formed on a square pyramid [J].Journal of Industrial Textiles, 2005, 35 (2): 115-135.

[8] POTLURI P, MANAN A. Mechanics of non- orthogonally interlaced textile composites [J].Composites: Part A, 2005, 34: 481-492.

[9] 王晓明, 邹婷, 李超婧, 等. 基于编织点起始位置及牵拉速度变化的编织角预测模型[J].纺织学报. 2015, 36(9): 28-33.

WANG Xiaoming, ZOU Ting, LI Chaojing, et al. Predicting model for braiding angle based on initial braiding height and take-up speeds[J].Journal of Textile Research, 2015, 36(9): 28-33.

[10] 孙志宏, 阮谷萍. 圆形编织法的工艺参数对编织物结构的影响[J].纺织学报, 1999, 20(6): 359-362.

SUN Zhihong, RUAN Guping. Effects of process parameters on the structure of woven fabric[J].Journal of Textile Research, 1999, 20(6): 359-362.

[11] FANG Gang Ning, PRASAD Potluri, YU Weidong, et al. Geometrical modeling of tubular braided structures using generalized rose curve[J]. Textile Research Journal, 2017, 87(4): 474-486.