应用优化霍夫变换的细纱断头检测

王雯雯， 刘基宏

(生态纺织教育部重点实验室(江南大学)， 江苏 无锡 214122)

细纱成纱过程中，断头是影响成纱质量的重要因素之一。现有的断头检测装置可分为电磁传感器、光电传感器、热敏传感器等，通过检测锭子上的运动元件从而判断是否断纱；巡回检测将检测装置安装在细纱机的一端，并在细纱机上安装导轨，带动检测装置做往复运动，完成纱线断头的检测[1-2]。虽然市场上的断头检测装置很多，也存在基于图像处理的断头检测装置，但至今还未推广使用，也没有检测断头的专用算法。

本文在前期研究的基础上，基于图像处理，根据巡回式检测断头装置，开发了一种针对细纱断头检测的专用算法。利用工业相机捕获细纱机纺纱时的纱线图像，在小波变换和霍夫变换的基础上进行纱线信息提取，判断纱线的断头情况。

1 断纱检测

1.1 实验装置构建

用于图像采集的设备为像素800万的Dscamdemo工业相机。工业相机通过USB接口与电脑相连，并通过电脑进行图像采集。细纱机为TH558型纺纱机，待测纱线为9.7 tex 精梳棉，锭速为11 000 r/min，捻系数为329。

图1为实验装置图。实验过程中，对细纱机的纺纱段进行图像采集，相机安装在可移动的小车上，小车边缘与细纱机底部距离为300 mm，相机高度与细纱机叶子板保持一致，镜头正对且平行于叶子板，并与导纱钩间的距离为560 mm。图2示出采集到的纱线图像。

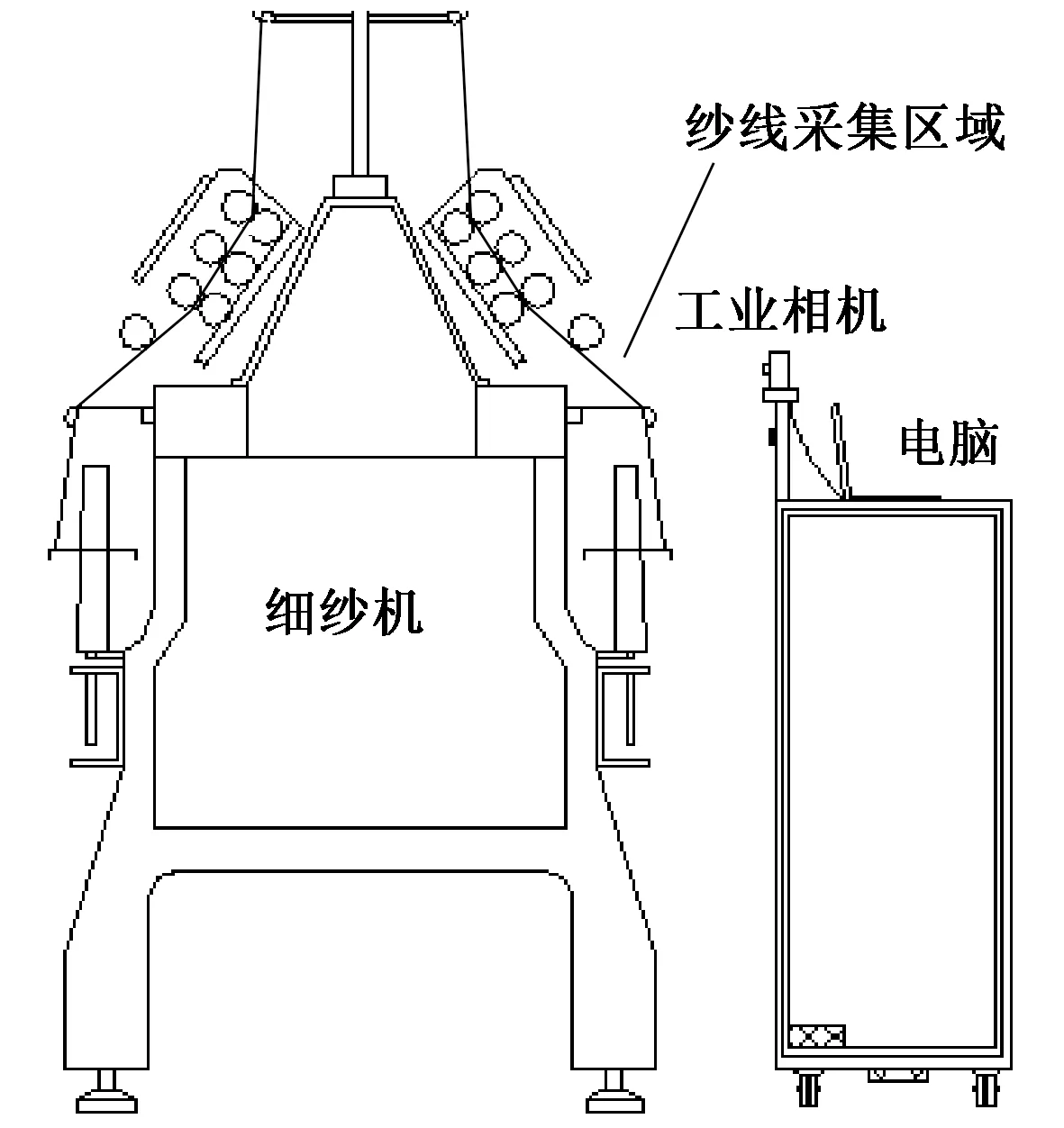
图1 实验装置图Fig.1 Construction of experimental apparatus

图2 采集的纱线图像Fig.2 Collected yarn image. (a) Normal spinning (3 yarns); (b) Normal spinning (2 yarns); (c) Broken yarn

1.2 断头检测流程

细纱机高速运行状态下进行图像采集，相机距纱线的距离以及纱线在纺纱过程中的高速运转可对采集到的图像质量造成干扰。通过观察采集到的原始图像发现：图像中噪声较多，严重干扰了纱线信息的提取；纱线运行稳定性差，采集到的纱线图像较静止时的图像直径更粗；同时，图像的亮度对其质量影响较大。

为方便后续纱线信息的提取，首先对图像进行去噪处理，平滑噪声的同时，保留纱线信息，提高图像质量；再进行优化霍夫直线提取，对提取的直线进行共线性检验确保纱线被准确提取出来，从而判断断纱情况。

1.3 图像去噪

小波分析用于图像去噪处理，主要是根据图像信号与噪声信号经小波变换后在不同分辨率条件下呈现不同的规律，通过在不同分辨率下设定阈值，调整小波系数，达到图像去噪目的[3-4]。图像去噪前将图2(a)转化为灰度图，如图3所示。

图3 灰度图像Fig.3 Grayscale image

二维连续小波函数为：

式中：α为尺度；τ为平移量。尺度α控制小波函数的伸缩，平移量τ控制小波函数的平移。

本文实验中采用sym4小波，设定纱线图像中信号为：

f(t)=s(t)+n(t)

式中：s(t)为纱线图像原始信号；n(t)为噪声信号。对f(t)连续做3次小波分解，分解后s(t)和n(t)分别有对应的小波系数wi,t。s(t)的小波系数wi,t较大值的位置，对应着原始图像中的奇变位置和重要信息[5]；而n(t)在每一层分解尺度上的wi,t值都是较小的，且分布一致，因此，选一合适的数δ，当小波系数wi,t小于阈值δ时，数值用零代替；大于阈值δ时，数值用δ来缩减。

式中：sgn (·) 是符号函数，当数值大于零时，符号为正，反之符号为负。图4示出灰度图像和小波、均值滤波去噪图像放大45倍后截取相同区域的图像。首先对图4(a)所示图像给定软阈值δ=10进行小波去噪处理。

图4 局部去噪效果对比Fig.4 Comparison of local denoising. (a) Grayscale image; (b) Mean filter denoising

为进一步平滑图像，对小波去噪图像再进行均值滤波去噪处理。均值滤波是对当前像素选择一个模板，该模板由其邻近的若干个像素组成，然后用模板的均值来替代原像素的值。

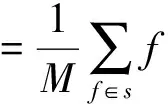
式中：M为模板中像素点的个数；f(x,y)为当前像素点的像素值；g(x,y)为均值滤波后该点的像素值；s为图像中所有像素点的集合。采用3像素× 3像素模板，即M为9，进行均值滤波去噪处理，得到图4(b)。通过观察发现，灰度图像中噪声有效地被平滑掉，纱线信息得到了有效保留。

1.4 霍夫变换提取直线

霍夫变换前首先对图像进行边缘检测，然后将图像转变成二值图像，待测图像如图5所示。图像中的纱线可看作是线状物体，通过霍夫变换来提取图像中的纱线信息。

图5 边缘检测图Fig.5 Edge detection graph

霍夫变换的基本思想为：图像空间x-y中，对于满足直线方程y=ax+b的某个数据点(x1,y1)，对应参数平面a-b上的1条直线b=y1-ax1，即直线L1，而对于y=ax+b直线上所有的点对应参数平面a-b上的所有直线一定会相交于点(a0,b0)[6-8]。

为避免垂直直线斜率无穷大的问题，在断纱检测时通常采用直线的极坐标方程ρ=xcos+ysinθ，此时参数平面为(ρ,θ)平面。对于边缘检测后的图像中(x1,y1)、(x2,y2)、(x3,y3)，将其代入ρ-θ坐标中，可得：

ρ=xcosθ+ysinθ=

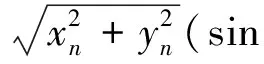
图6 霍夫空间图Fig.6 Hough space graph

在霍夫变换矩阵中，设定极值点为3个，在绘制直线时，设定直线长度为图像高度，直线颜色为白色，检测直线图如图7所示。

图7 霍夫变换检测直线图Fig.7 Hough transform detection line graph. (a) Before breakage; (b) Broken yarn

1.5 断纱的判定

小车以10 cm/s的速度缓慢前进，前进过程中对纱线进行连续拍摄，采集到的图像存在正常纺纱图像和断纱图像，断纱根数为1、2、3，暂不讨论断纱根数为2和3的情况。

当发生1根断纱时，相机在来回移动过程中会采集到如图2(c)所示的图像；但是纺纱机正常纺纱时，图像中也可能出现只存在2根纱线的情况，如图2(b)，这是相机刚移动过第1根纱线，下一根带检测的纱线还未进入相机拍摄范围时采集到的图像。针对这2种情况，存在

L=xi-xi+1

式中，xi为第i根纱线的最下端像素点的横坐标。当L>500时，图像中出现断纱；当L≤500时，未发生断纱。

2 参数讨论

2.1 小波去噪的阈值及分解层数选择

选取不同的阈值δ对图像进行小波去噪，并对比各阈值小波去噪图像与原始灰度图像的峰值信噪比(PSNR)，如图8所示。

PSNR值越大，图像去噪效果越好。由图8(a)可发现，在δ≥10后PSNR增大的趋势陡然上升，但是在δ为13、15时，图像中的部分有效信息被消除，无法准确检测出直线的存在。δ=10时，图像中的噪声被有效消除，且保留了有效信息，因此，选择δ=10 作为小波去噪的阀值。

对于小波去噪的分解层数s，分别选取s为2、3、4、5、6对图像进行去噪，其峰值信噪比如图8(b)所示，在不同分解层数下，程序运行时间如表1所示。

由图8(b)可发现，PSNR值呈上升趋势，但是上升幅度较小，说明分解层数对去噪效果影响不大。当s=6时，PSNR值最大，即去噪效果最好。对比各个分解层数下程序运行时间，在分解层数为5和6时，虽然去噪效果较好，但程序运行时间大大增加。

图8 不同阈值和分解层数条件下的去噪图像与原图信噪比Fig.8 Different denoising images and original signal-to-noise ratio under different thresholds and decomposed layer. (a) Different threshholds; (b) Different decomposed layer

分解层数运行时间/s2根纱线3根纱线2237542075232675424546438753407875758767423467456778675

衡量分解层数对PSNR和运行时间的影响后，选择s=3 作为小波去噪的分解层数。

2.2 边缘检测算子的选择

在自由边缘检测中，检测出纱线背景叶子板对霍夫变换提取直线产生干扰并增加了计算量，其检测图如图9所示。由于图像中的纱线基本处于垂直方向，为避免不必要的运算，提高霍夫变化运算速度，在进行边缘检测时，通过prewitt算子将检测方向设定为垂直，避免了水平方向直线的干扰(见图7(a))。

图9 自由边缘检测后霍夫变换检测直线图Fig.9 Hough transform detection line graph after free edge detection

2.3 霍夫变换检测角度的影响

纱线图像在拍摄过程中，相机移动或纱线抖动可造成图像中纱线的倾斜，但倾斜角度不会过大。通过霍夫变换对边缘检测的二值图像上的点在[-10°,10°]方向上进行直线检测，并将变换的间隔角度设定为4°，霍夫空间图如图10所示。通过缩短霍夫检测的角度和扩大间隔角度，霍夫变换运算时间由0.46 s减少到了0.31 s，降低了运算时间，提高了运算速度。

图10 优化后的霍夫空间图Fig.10 Optimized Hough space diagram

2.4 共线性检测

采用细纱机纺纱时，钢丝圈带动纱线高速运动进行加捻卷绕。纱线运动过程中由于锭速、牵伸倍数等参数设定不合理，纱线运动稳定性较差，工业相机拍摄不稳定等原因，造成捕获的纱线图像存在模糊虚影，导致二值图像中纱线的直径增大。当细纱机存在断纱时，对于存在虚影的纱线，通过霍夫变换提取直线时，由于峰值设定为3，可能出现如图11所示的情况，断头情况将无法正确判别。

图11 纺纱不稳定时的霍夫变换检测直线图Fig.11 Hough transform detection line diagram when spinning unstable

针对这一问题，在霍夫变换后对图像进行共线性检验。对霍夫变换检测出的直线标记为 flag(i)，设定直线起点横坐标为xi，终点横坐标为yi，存在：

V=(xi-xi+1)(yi-yi+1)

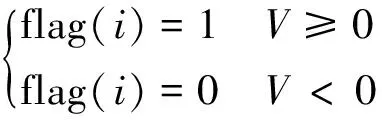
式中，flag(i)=1时，霍夫变换检测出的直线为有效线段。经过共线性检测后的霍夫变换图像如图9(b)所示，有效排除了纱线运动的干扰，准确地提取了纱线信息。

3 结 论

基于霍夫变换原理，本文提出了一种细纱断头检测方法。采用小波滤波和霍夫变换可准确提取纱线断头信息。通过平滑去噪和共线性检验，可从被噪声干扰的纱线图像中得到准确的纱线。实验表明该方法在一定亮度范围内，对3根纱线的断头情况判断是准确的，可为将来实现断纱检测提供参考。

FZXB

参考文献：

[1] 宋晓亮, 刘建立, 徐阳, 等. 光电式环锭断纱在线检测系统[J]. 纺织学报, 2014,35(8): 98-103.

SONG Xiaoliang, LIU Jianli, XU Yang, et al.On-line detecting system based on optoelectronic technology for ring spun-yarn breakage[J]. Journal of Textile Research, 2014,35(8): 98-103.

[2] 李强, 杨艺, 刘基宏, 等. 赛络纺粗纱断纱在线检测[J]. 纺织学报, 2016, 37(10): 120-124.

LI Qiang,YANG Yi,LIU Jihong, et al. Online detection of roving strand broken in siro-spinning[J]. Journal of Textile Research,2016, 37(10):120-124.

[3] 傅嘉政, 杨少敏, 刘浩. 基于小波变换和霍夫变换的高分辨率遥感影像道路提取[J]. 测绘地理信息, 2015(4): 48-50, 53.

FU Jiazheng,YANG Shaomin,LIU Hao. High-resolution remote sensing images road extraction based on wavelet transform and hough transform[J]. Journal of Geomatics, 2015(4): 48-50, 53.

[4] 章浙涛, 朱建军, 匡翠林, 等. 小波包多阈值去噪法及其在形变分析中的应用[J]. 测绘学报,2014(1): 13-20.

ZHANG Zhetao, ZHU Jianjun, KUANG Cuilin, et al. Multi-threshold wavelet packet de-noising method and its application in deformation analysis[J]. Acta Geodaeticaet Cartographica Sinica, 2014(1): 13-20.

[5] 孙继平, 佘杰. 基于小波的煤岩图像特征抽取与识别[J]. 煤炭学报, 2013(10): 1900-1904.

SUN Jiping,SHE Jie. Wavelet-based coal-rock image feature extraction and recognition[J].Journal of China Coal Society, 2013(10): 1900-1904.

[6] 庞存锁, 侯慧玲, 韩焱. 基于霍夫变换的高速微弱目标检测算法[J]. 电子与信息学报, 2012(3): 754-757.

PANG Cunsuo, HOU Huiling, HAN Yan. High-speed weak target detection based on hough transform[J]. Journal of Electronics & Information Technology, 2012(3): 754-757.

[7] 李建, 张其栋. 基于霍夫变换的遥感图像城市道路的提取识别[J]. 电脑知识与技术, 2017 (3): 172-174.

LI Jian, ZHANG Qidong. Extracting and identifying urban roads from remote sensing images based on hough transform[J]. Computer Knowledge and Technology, 2017(3): 172-174.

[8] 唐春锦. 融合提升小波和霍夫变换的磨粒纹理提取及识别[D]. 南京：南京航空航天大学, 2015:47-48.

TANG Chunjin. Texture extraction and identification of wear particles by combining lifting wavelet and hough transform[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2015: 47-48.

[9] 亢伉. 一种改进快速Hough变换的车道线检测算法[J]. 宝鸡文理学院学报(自然科学版), 2014(2): 62-65.

KANG Kai. Lane detection algorithm based on modified fast Hough transformation[J]. Journal of Baoji University of Arts and Sciences(Natural Science Edition), 2014(2): 62-65.

[10] 王越, 黄龙超, 李琴. 基于区域划分和霍夫变换的车牌倾斜校正[J]. 重庆理工大学学报(自然科学版), 2017(3): 97-104.

WANG Yue, HUANG Longchao, LI Qin. License plate tilt correction based on region partition and hough transform[J]. Journal of Chongqing University of Technology(Natural Science Edition), 2017(3): 97-104.